Formes Géométriques

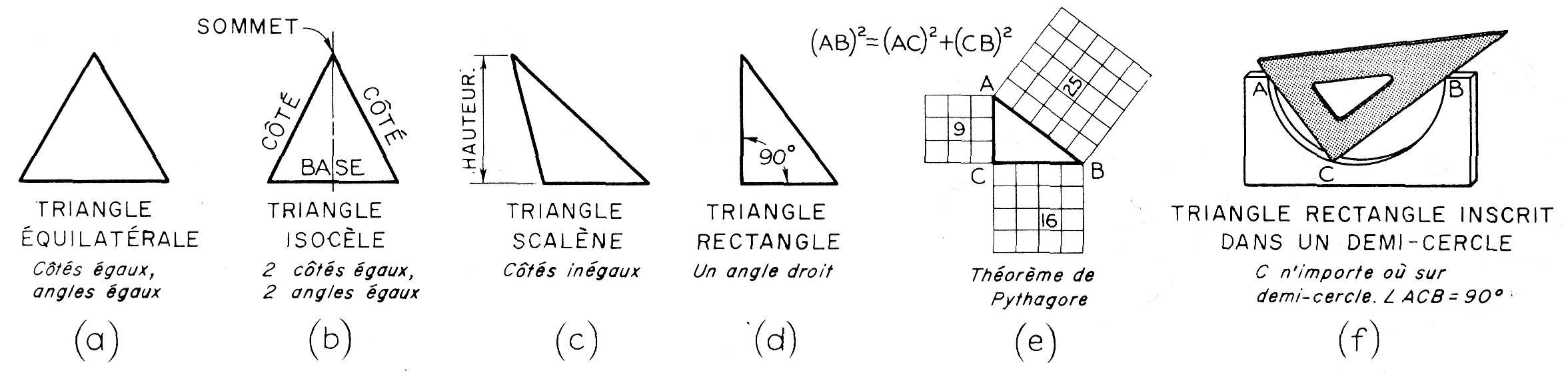
Triangles (Figure 4.3). Le triangle est une figure plane limitée par trois côtés droits.

Figure 4.3
Triangles

La somme des angles intérieurs est toujours de 180°. Un triangle rectangle (d) possède un angle de 90° et le carré de son hypoténuse est égal à la somme des carrés des deux côtés (e). Comme l'illustre la figure 4.3.f, tout triangle inscrit dans un demi-cercle est rectangle, si son hypoténuse est confondue avec le diamètre.

Quadrilatères (Figure 4.4). Le quadrilatère est une figure plane limitée par quatre côtés droits. Si les côtés opposés sont parallèles, le quadrilatère est alors appelé parallélogramme.

Figure 4.4
Quadrilatères

Polygones (Figure 4.5). Le polygone est toute figure plane limitée par des côtés droits. Un polygone régulier possède des côtés égaux et des angles égaux; il peut soit être inscrit dans un cercle soit circonscrire un cercle.

Figure 4.5
Polygones réguliers

Cercles et arcs (Figure 4.6). Le cercle (a) est une figure plane limitée par une courbe fermée, dont tous les points sont à égale distance d'un point fixe intérieur appelé centre. La circonférence d'un cercle désigne la courbe fermée dont la longueur totale est de 3,1416 (ou plus exactement n) fois le diamètre du cercle. D'autres définitions sont fournies à la figure 4.6.

Figure 4.6
Cercles

Solides (Figure 4.7). Le solide est une figure à trois dimensions limitée par des surfaces fermées. Si les surfaces sont composées de portions de plans, appelées faces ou facettes, le solide est un polyèdre. Un polyèdre régulier est un polyèdre dont toutes les faces sont des polygones réguliers égaux.

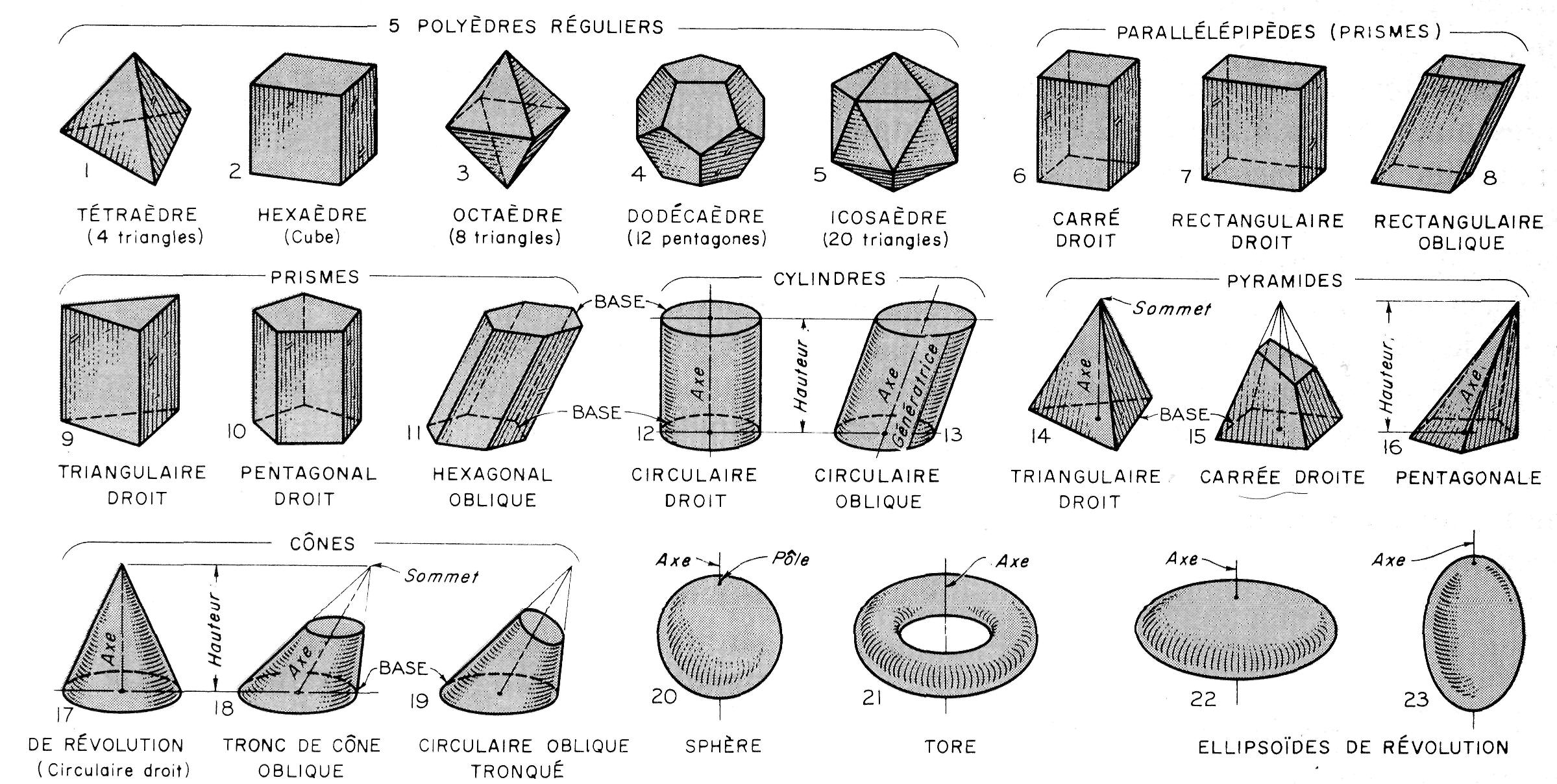
Figure 4.7
Solides

Le prisme possède deux bases parallèles, formées par des polygones réguliers, et des faces latérales qui sont des parallélogrammes. Le prisme triangulaire a des bases triangulaires, le prisme rectangulaire a des bases rectangulaires, etc. Le parallélépipède a des bases en forme de parallélogramme. Le prisme droit possède des arêtes latérales qui sont perpendiculaires aux bases, tandis que les arêtes latérales du prisme oblique sont obliques par rapport aux bases. Si un bout du prisme est retranché par un plan qui n'est pas parallèle aux bases, le prisme est dit tronqué.
La pyramide est un solide qui a pour base un polygone plan et pour faces latérales, des triangles qui se réunissent en un point commun, le sommet. La hauteur de chaque face triangulaire est appelée apothème.

La ligne qui joint le centre de la base au sommet est appelé l'axe de la pyramide. Si l'axe est perpendiculaire à la base, la pyramide est droite, sinon elle est oblique.

Une pyramide régulière est une pyramide droite dont la base est un polygone régulier. Une pyramide triangulaire a comme base un triangle, une pyramide rectangulaire, un rectangle, etc. Le tronc d'une pyramide est la portion du volume de la pyramide compris entre la base et un plan parallèle à la base. Si le plan sécant n'est pas parallèle à la base, la pyramide est dite tronquée.

Le cylindre est un solide limité par deux plans parallèles et par une surface qui est engendrée par une droite, la génératrice, se déplaçant parallèlement à elle-même et toujours en contact avec une courbe fermée, la directrice. Un cylindre de révolution est engendré par la rotation d'un rectangle autour d'un de ses côtés. Les deux bases sont alors circulaires et perpendiculaires à l'axe du cylindre.

Le cône était autrefois défini comme un volume, mais, de nos jours, il est surtout considéré comme une surface engendrée par une droite mobile, la génératrice, passant par un point fixe appelé sommet du cône, et s'appuyant sur une courbe fixe, la directrice.

La sphère est générée par la rotation d'un cercle autour d'un de ses diamètres. Ce diamètre est l'axe de la sphère. Les deux extrémités de l'axe sont les pôles de la sphère.

Le tore est un solide engendré par un cercle (ou d'autre courbe fermée) tournant autour d'un axe situé dans son plan et ne passant pas par son centre.