Le cercle circonscrit est donné.

Figure 4.25.a.

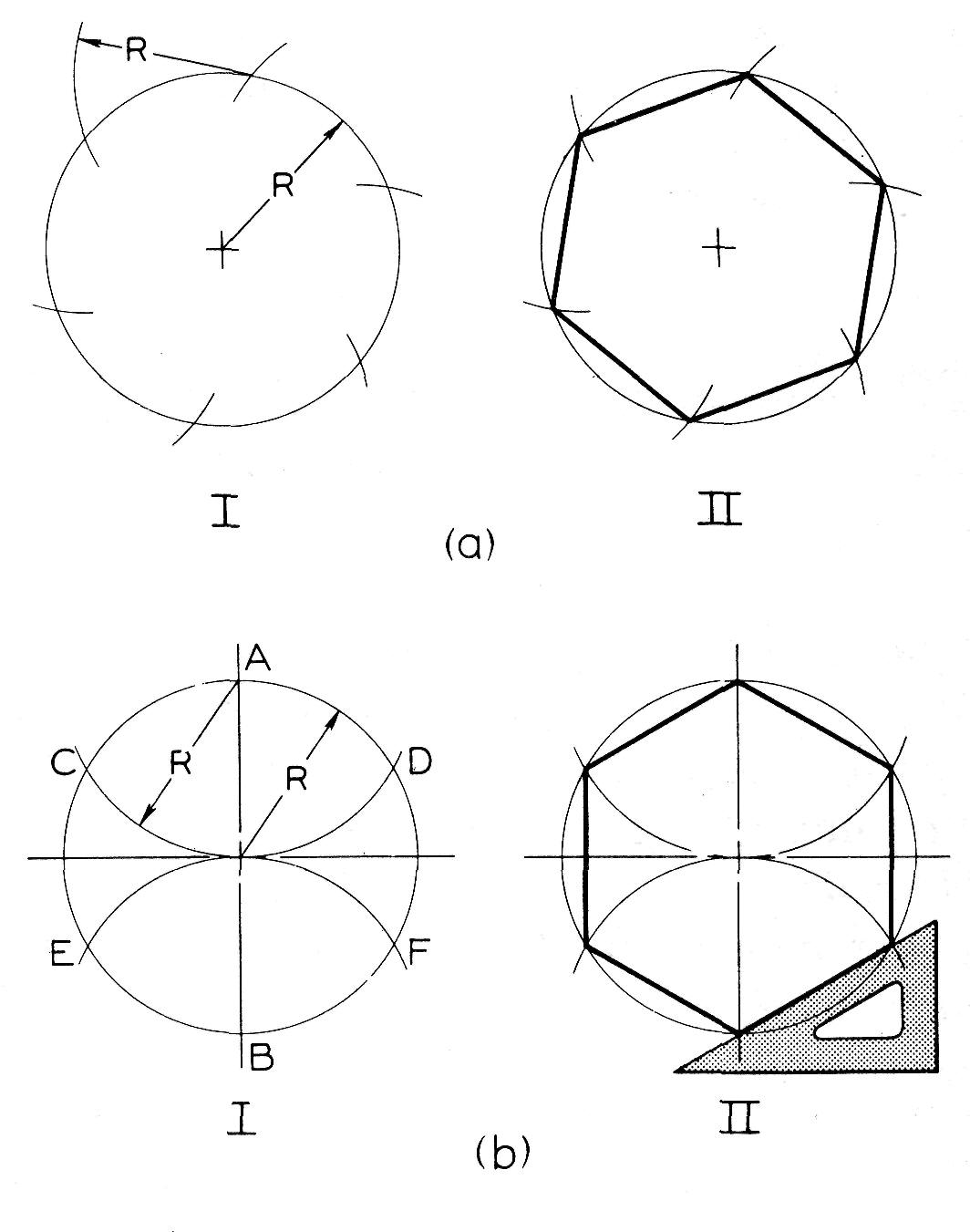
Figure 4.25
Tracé d'un hexagone régulier

Chaque côté d'un hexagone est égal au rayon du cercle circonscrit. Par conséquent, à l'aide d'un compas et à partir du rayon du cercle, rapportez les six côtés de l'hexagone sur la circonférence et reliez les points par des droites. Pour vérifier la précision, il faut s'assurer que les côtés opposés de l'hexagone sont parallèles.

Méthode pratique (Figure 4.25.b). Cette construction est une variation de celle illustrée en (a). Tracez les axes de symétrie vertical et horizontal. De A et B comme centres et à partir d'un rayon égal à celui du cercle, tracez des arcs qui coupent le cercle en C, D, E et F; complétez l'hexagone comme l'illustre la figure.

Le cercle circonscrit ou le cercle inscrit étant déterminé, les méthodes qui suivent sont toutes deux recommandées.
Figures 4.26.a et 4.26.b.

Figure 4.26
Tracé d'un hexagone régulier

Le cercle circonscrit est donné (distance « sur angles»). Tracez les axes vertical et horizontal, puis les diagonales AB et CD à des angles de 30° et 60° avec l'horizontale; ensuite, à l'aide de l'équerre à 60° et du té, tracez les six côtés.

(Figures 4.26.C et 4.26.d) Le cercle inscrit est donné (longueur « sur plats »). Tracez les axes vertical et horizontal; puis, à l'aide de l'équerre à 60° et du té, tracez les six côtés tangents au cercle. Cette méthode est employée pour le dessin des têtes de boulon et des écrous (section 13.26). Pour un maximum de précision, on peut ajouter des diagonales comme en (a) et en (b).

Autre Méthode

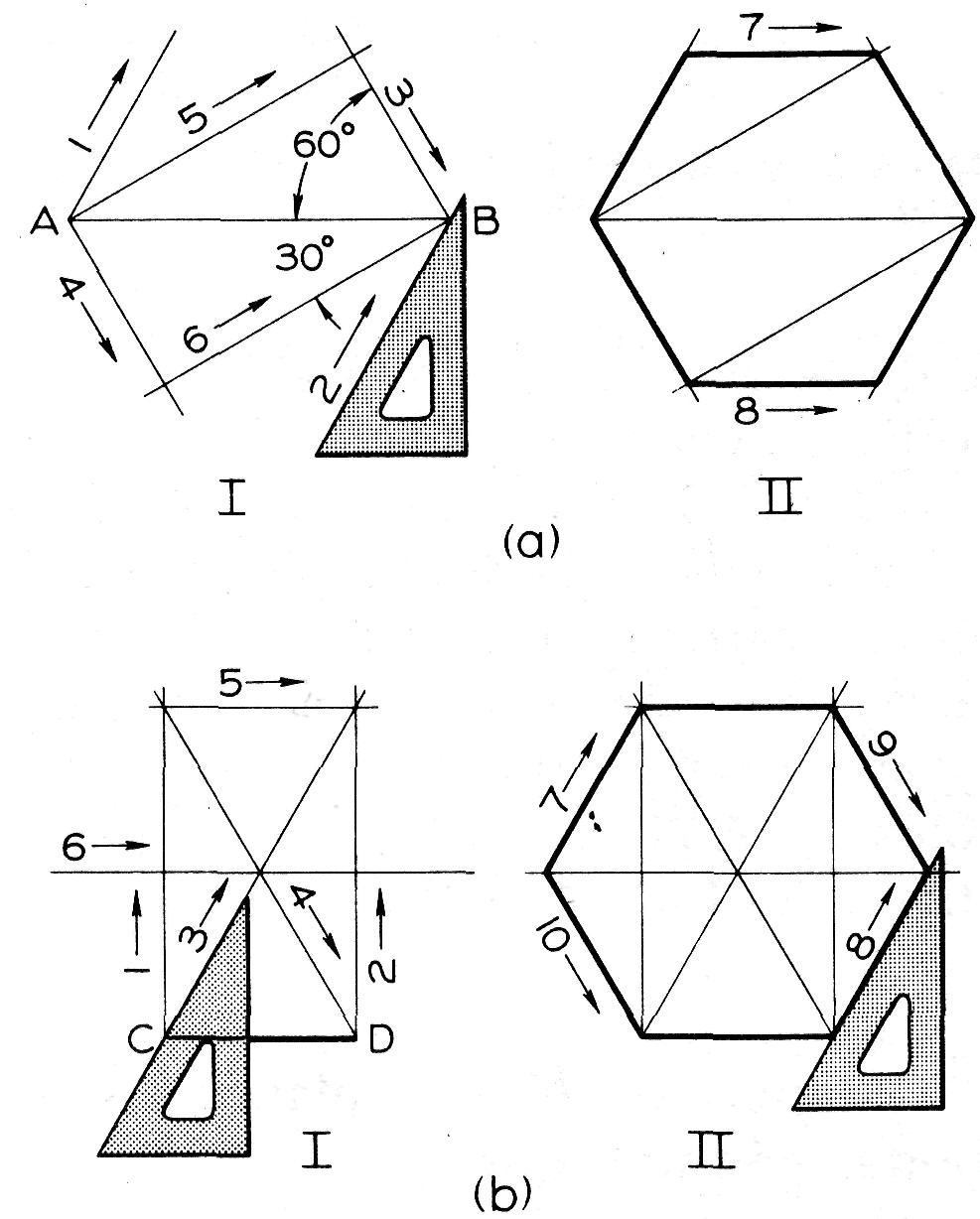
Figure 4.27
Tracé d'un hexagone régulier

A l'aide de l'équerre à 60° et du té, tracez des lignes soit en suivant l'ordre indiqué en (a), où la distance AB est donnée, soit comme en (b), où le côté CD est donné.