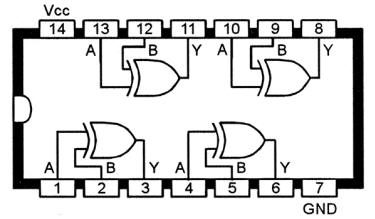
Circuit Intégrée XOR et XNOR
Les tampon numérique, les portes logiques et les IC logiques
La sortie d'une porte XOR ne passe à l'état haut que lorsque ses deux entrées sont à des niveaux logiques différents.
Les circuits intégrés de porte XOR les plus largement utilisés sont les types 74LS86 TTL et 74HC86 et 4070B CMOS.
Schéma fonctionnel du IC de porte XOR 74LS86 ou 74HC86

Schéma fonctionnel du IC de porte XOR 4070B

Si une ou plusieurs portes d'un CMOS XOR sont inutilisées, elles peuvent être désactivées en mettant simplement les deux entrées à la terre.
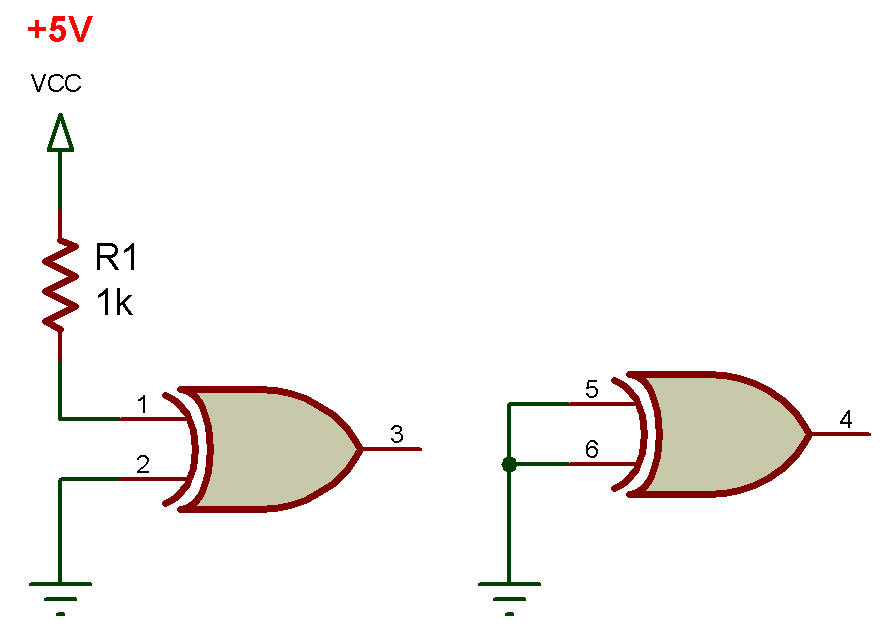
Dans le cas d'un CI TTL XOR, il est préférable de désactiver les portes inutilisées en mettant à la terre une borne d'entrée et en attachant l'autre à un niveau haut via une résistance 1K, comme le montre la figure ci-dessous, car cela entraîne une consommation de courant de repos minimale.
Alternativement, si la consommation de courant n'est pas importante, les deux entrées peuvent simplement être reliées à la terre comme indiqué.
Deux façons de désactiver les portes TTL XOR
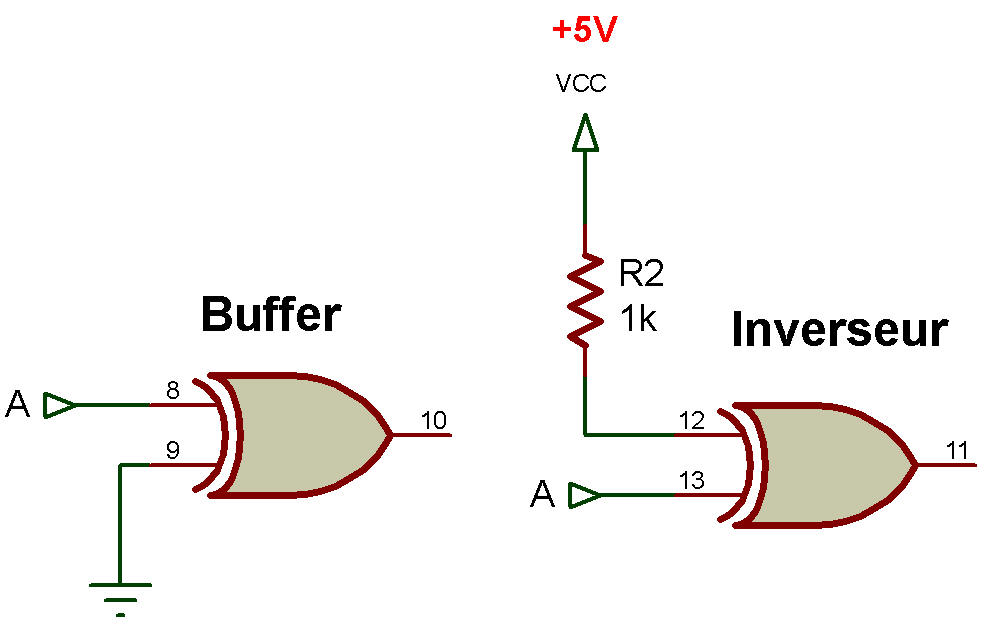
Les portes XOR sont assez polyvalentes. Une porte XOR peut être utilisée pour agir comme un tampon non inverseur en mettant simplement à la terre son entrée inutilisée, comme le montre la figure ci-dessous, ou comme un tampon inverseur en attachant l'entrée inutilisée à un niveau haut (via une résistance de 1K en TTL) comme le montre la figure ci-dessou.
Façons d'utiliser les portes TTL XOR comme tampons ou inverseurs
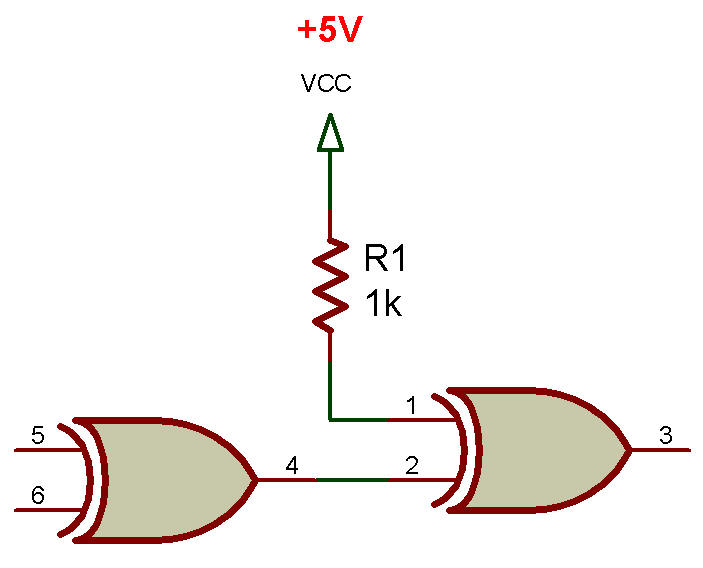
Deux portes XOR peuvent être utilisées pour créer une seule porte XNOR en les connectant comme le montre la figure ci-desous, où la porte de droite est utilisée pour inverser la sortie de la porte de gauche.
Notez que les circuits intégrés CMOS Quad XNOR sont également disponibles sous forme de circuits intégrés dédiés comme le 4077B et le 74HC266, mais que les portes de ces derniers circuits intégrés ont des sorties à drain ouvert.
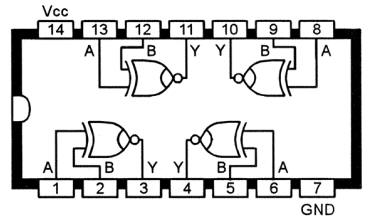
Schéma fonctionnel du circuit intégré de porte Quad XNOR 4077B

Schéma fonctionnel du circuit intégré à porte Quad EX-NOR 74HC266 avec sorties à drain ouvert (o.d.)
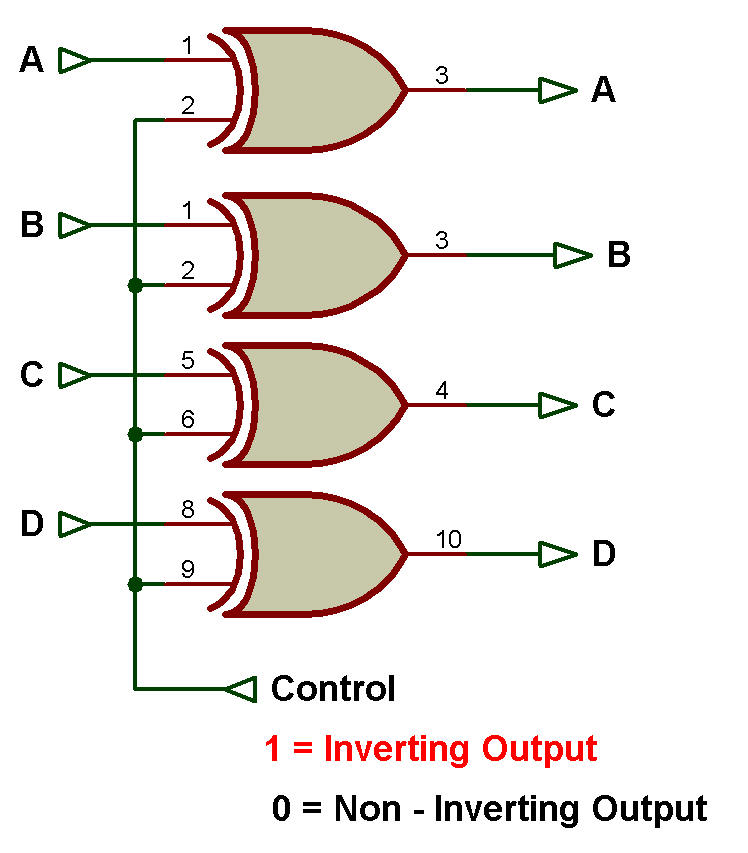
Les figures ci-dessous montrent deux autres applications utiles de la porte EX-OR.
Sur la figure ci-dessous, quatre portes XOR sont alimentées par un signal de commande commun qui permet à un code d'entrée « ABCD » de quatre bits d'être présenté sous la forme d'une sortie ABCD vraie (directe) ou complémentaire (inversée), rendant ainsi le Sorties True/Complement à quatre bits disponibles via cinq (au lieu de huit) bornes.
Le circuit de la figure ci-dessous compare simplement les états logiques des deux mots de quatre bits et donne une sortie logique 0 si les deux mots sont identiques, et une sortie logique 1 s'ils diffèrent.
 .
.
L'une des applications les plus importantes de la porte XOR est celle d'additionneur binaire.
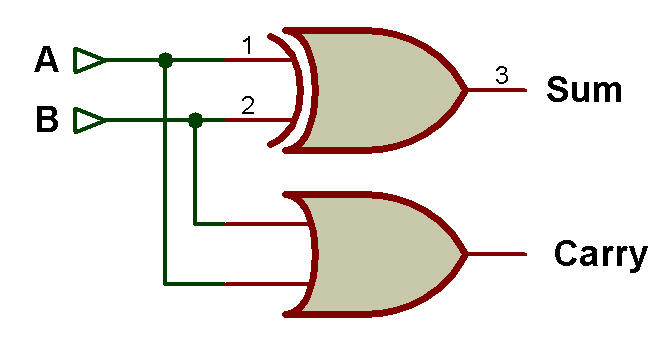
Ci-dessous il y a les règles de base de l'addition binaire et la figure ci-dessous montre comment une porte XOR et AND peut être utilisée pour créer un circuit demi-additionneur pratique qui peut additionner deux entrées binaires ensemble et générer des sorties SUM et CARRY.
Règles de base de l'addition binaire
0 + 0 = 0
0 + 1 = 1
1 + 0 = 1
1 + 1 = 0, Carry = 1
Circuit demi-additionneur binaire
| A | B | Sum | Carry |
| 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
Le circuit est appelé demi-additionneur car il ne peut effectuer qu’une forme d’addition très primitive qui ne lui permet pas d’accepter une entrée de report provenant d’un étage d’addition précédent.
Un additionneur complet est un circuit beaucoup plus utile qui peut accepter une entrée de report, effectuer une addition binaire sur deux bits et générer une sortie de report ; ces circuits sont entièrement cascadables, permettant à des groupes de circuits d'effectuer une addition binaire sur des nombres numériques de n'importe quelle largeur de bits souhaitée.
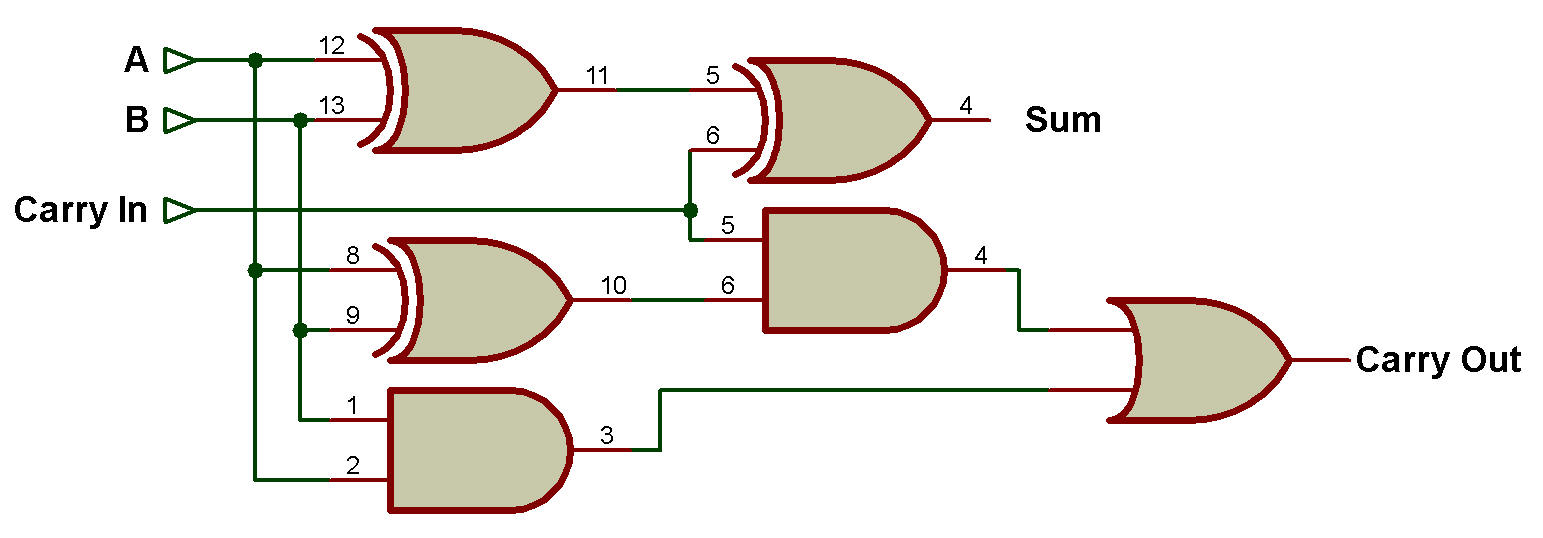
La figure ci-dessous montre une façon de construire un circuit additionneur complet à deux bits, en utilisant trois portes XOR, deux portes ET et une porte OU.
En pratique, des additionneurs complets à quatre bits sont facilement disponibles sous la forme des circuits intégrés 74LS283 et 4008B.
Circuit additionneur complet et table de vérité
| A | B | Carry In | Sum | Carry Out |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 | 0 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 | 1 |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 |
