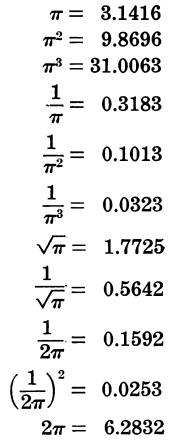
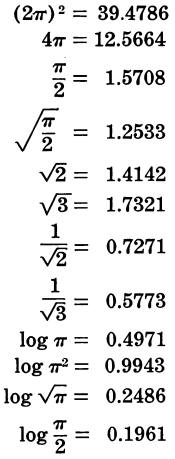
Mathematics and formulas data
MATHEMATICAL CONSTANTS
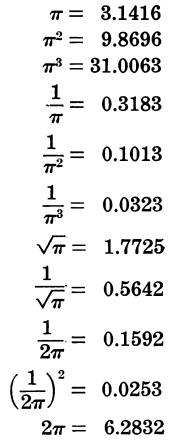
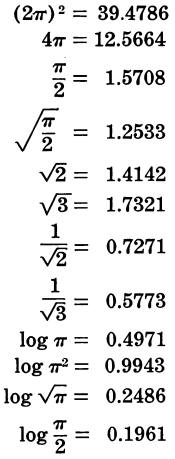
MATHEMATICAL SYMBOLS

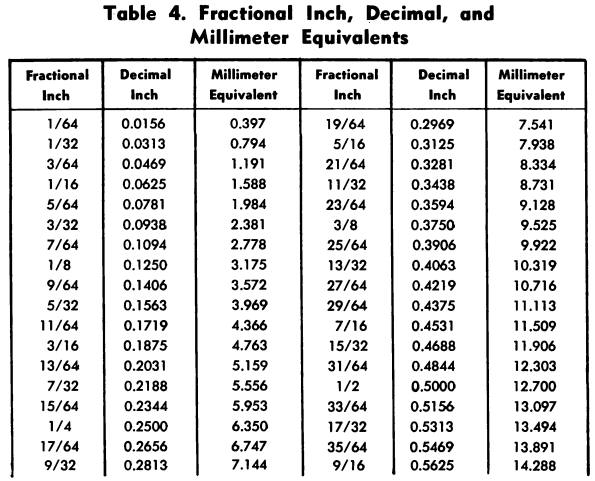
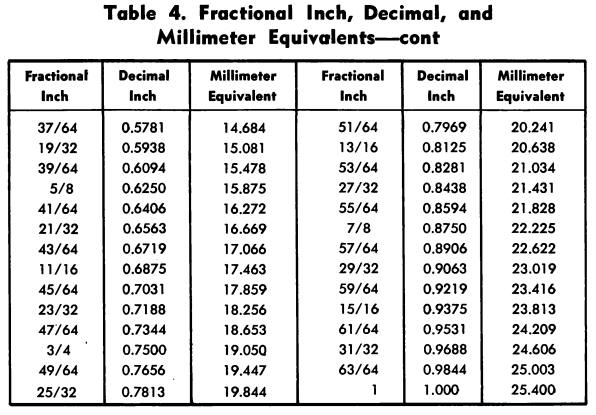
FRACTIONAL INCH, DECIMAL, AND MILLIMETER EQUIVALENTS
Table 4 gives the decimal inch and millimeter equivalents of fractional parts of an inch by 64ths, to four significant figures.
POWERS OF TEN
Exponent Determination Large numbers can be simplified by using powers of ten. For example, some of the multiples of ten from 1 to 1,000,000, with their equivalents in powers of ten are:
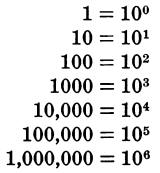
Likewise, powers of ten can be used to simplify decimal expressions. Some of the submultiples of ten from 0.1 to 0.000001, with their equivalents in powers of ten are:

Addition and Subtraction
To add or subtract using powers of ten, first convert all numbers to the same power of ten. The numbers can then be added or subtracted, and the answer will be in the same power of ten.
For example:
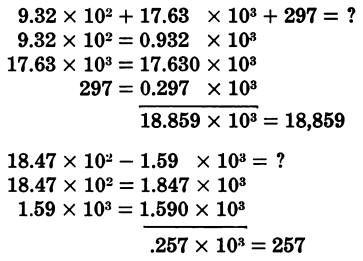
Multiplication
To multiply using powers of ten, add the exponents.
Thus:
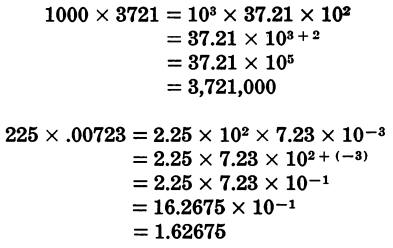
Division
To divide using powers of ten, subtract the exponent of the denominator from the exponent of the numerator.
Thus:
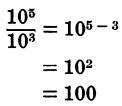
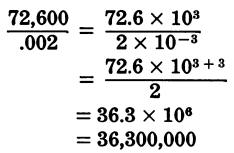
Combination Multiplication and Division
Problems involving a combination of multiplication and division can be solved using powers of ten by multiplying and dividing, as called for, until the problem is completed.
For example:
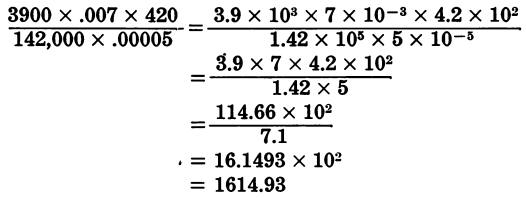
Reciprocal
To take the reciprocal of a number using powers of ten, first (if necessary) state the number so the decimal point precedes the first significant figure of the number.
Then divide this number into 1.
The power of 10 in the answer will be the same value as in the original number, but will have the opposite sign.
For example:

Square and Square Root
To square a number using powers of ten, multiply the number by itself, and double the exponent.
Thus:
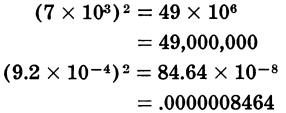
To extract the square root of a number using powers of ten, do the opposite.
If the number is an odd power of 10, first convert it to an even power of ten.
Extract the square root of the number, and divide the power of ten by 2.
Thus:
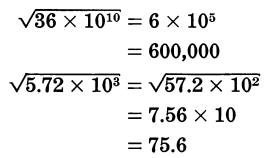
ALGEBRAIC OPERATIONS
Transposition of Terms
The following rules apply to the transposition of terms in algebraic equations:
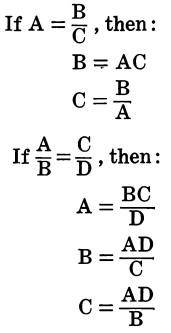
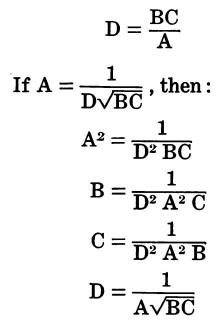
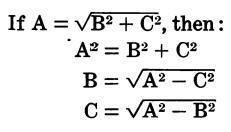
Laws of Exponents
A power of a fraction is equal to that power of the numer- ator divided by the same power of the denominator.
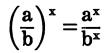
The product of two powers of the same base is also a power of that base; the exponent of the product is equal to the sum of the exponents of the two factors.
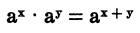
The quotient of two powers of the same base is also a power of that base; the exponent of the quotient is equal to the numerator exponent minus the denominator exponent.
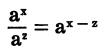
The power of a power of a base is also a power of that base; the exponent of the product is equal to the product of the exponents.
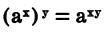
A negative exponent of a base is equal to the reciprocal of that base, with a positive exponent numerically equal to the original exponent.
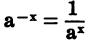
A fractional exponent indicates that the base should be raised to the power
indicated by the numerator of the
fraction; the root indicated by the
denominator should then be extracted.
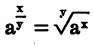
A root of a fraction is equal to the identical root of the numerator divided by the identical root of the denominator.
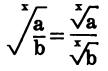
A root of a product is equal to the product of the roots of the individual factors.
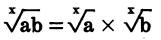
Quadratic Equation
The general quadratic equation:
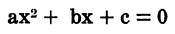
may be solved by:
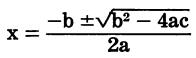
GEOMETRIC FORMULAS
| Triangle | Square | Rectangle |
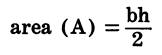 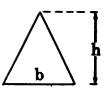 |
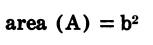 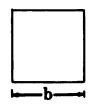 |
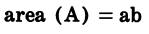 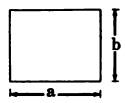 |
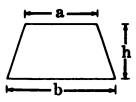
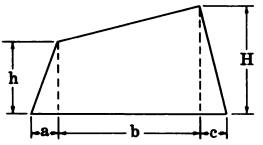
| Parallelogram | Trapezoid | Trapezium |
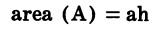 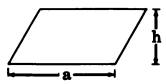 |
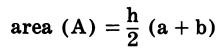  |
  |
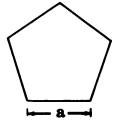
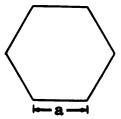
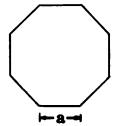
| Regular Pentagon | Regular Hexagon | Regular Octagon |
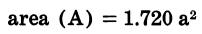  |
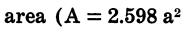  |
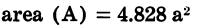  |
| Circle | Segment | Sector |
  |
  |
 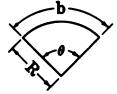 |
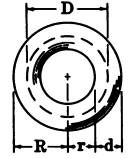
| Circular Ring | Ellipse | Sphere |
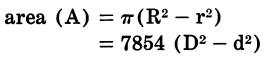 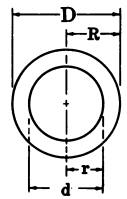 |
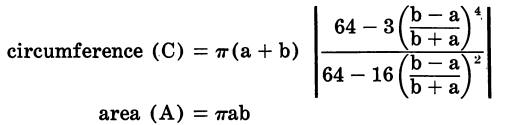 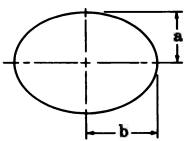 |
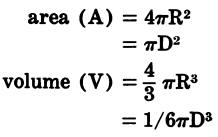  |
| Cube | Rectangular Solid | Cone |
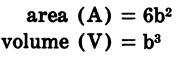 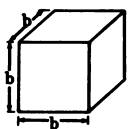 |
  |
  |
| Cylinder | Ring of Rectangular Cross Section |
Torus (Ring of Circular Cross Section) |
 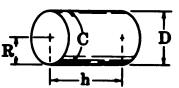 |
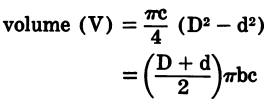 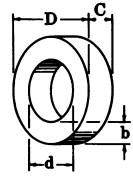 |
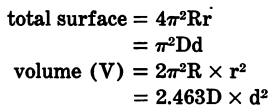  |
