Chapitre 5 - les circuits mixtes
Mon premier cours en électronique
Dans de nombreux circuits, certains des composants sont connectés en série pour être parcourus par le même courant, tandis que d'autres sont en parallèle pour être soumis à la même tension. La figure 5-1 en donne un exemple.
Figure 5-1 Circuit mixte:
(a) photographie du montage; (b) schéma;

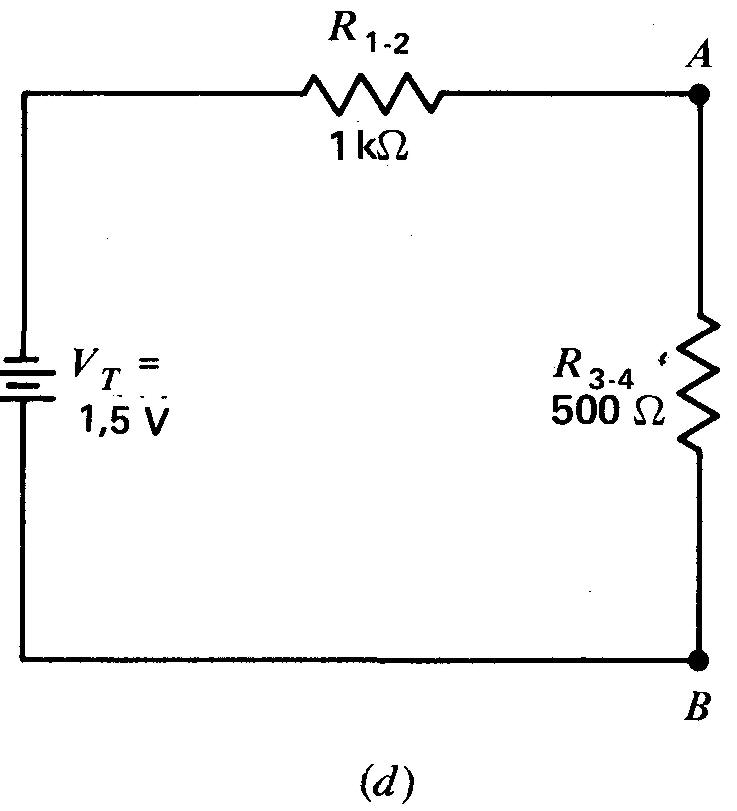
(c) l'addition des résistances en série R1 et R2 donne R1-2,
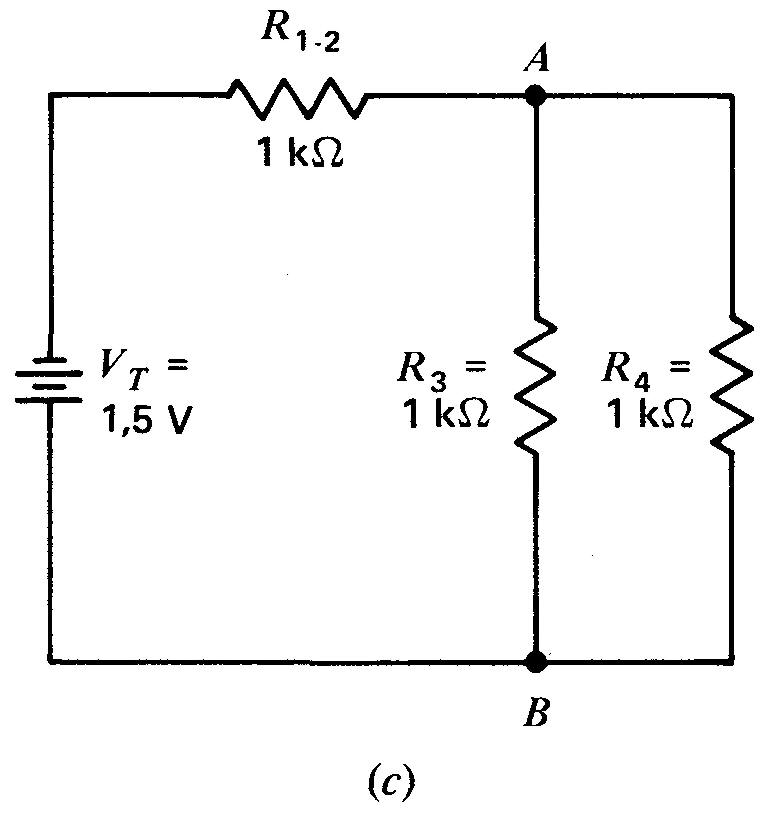
(d) la combinaison des résistances en parallèle R3 et R4 donne R3-4.
On utilise ce type de circuit quand il faut obtenir des tensions et des courants différents à partir d'une seule source de tension appliquée.
Les caractéristiques principales des circuits série et parallèle sont expliquées dans les sections suivantes:
5.1 Trouver RT pour des résistances en montage mixte
5.2 Jeux de résistances en série montés en parallèle
5.3 Jeux de résistances en parallèle montés en série
5.4 Jeux de résistances en parallèle et en série en montage mixte
5.5 Analyse des circuits mixtes
5.6 Le pont de Wheatstone
5.7 Connexions à une masse commune
5.8 Tensions mesurées par rapport à la masse du châssis
5.9 Circuits ouverts et courts-circuits dans les circuits mixtes
5.1 TROUVER RT POUR DES RÉSISTANCES EN MONTAGE MIXTE
Sur la figure 5-1, R1 est en série avec R2, R3 est en parallèle avec R4.
Mais, R2 n'est pas en série avec R3 ni avec R4.
Ceci, parce qu'au noeud A, le courant qui traverse R2 se partage entre R3 et R4. Il en résulte que le courant dans R3 est beaucoup plus faible que le courant dans R2.
Par conséquent, R2 et R3 ne peuvent pas être en série puisqu'elles ne sont pas traversées par le même courant. Pour la même raison, R4 ne peut pas être en série avec R2.
Pour trouver RT, on ajoute les résistances en série et on combine les résistances en parallèle.
À la figure 5-1c, les résistances R1 de 0,5 kΩ et R2 de 0,5 kΩ en série font un total de 1 kΩ pour R1-2.
On peut aussi combiner les résistances en parallèle, R3 de 1 kΩ et R4 de 1 kΩ, pour obtenir une résistance équivalente de 0,5 kΩ pour R3-4 , comme on l'indique à la figure 5-1d.
Cette combinaison parallèle R3-4 de 0,5 kΩ, est alors ajoutée à la combinaison série R1-2 de 1 kΩ, pour donner la valeur finale de RT de 1,5 kΩ
Une fois RT connu, on peut calculer le courant IT délivré dans la ligne principale par la source de 1,5 V.
On a IT = VT / RT, donc
IT = 1,5 V /1,5 kΩ, soit 1 mA.
Ce courant IT de 1 mA traverse R1 et R2.
Le courant IT de 1 mA se partage, au noeud A, en deux courants de branche de 0,5 m A qui circulent dans chacune des résistances R3 et R4.
Au noeud B, les deux courants partiels de 0,5 mA se recombinent pour former le courant IT de 1 mA qui circule dans la ligne principale, et retourne vers la source VT.
Problèmes pratiques 5.1 (réponses à la fin du chapitre) Considérer la figure 5-1 :
(a) Calculer la résistance équivalente aux résistances en série R1 et R2;
(b) Calculer la résistance équivalente aux résistances en parallèle R3 et R4;
(c) Calculer RT aux bornes de la source de VT.
5.2 JEUX DE RÉSISTANCES EN SÉRIE MONTÉS EN PARALLÈLE
L'exemple de la figure 5-2 montre plus en détail les tensions et les courants d'un circuit mixte. Supposons que quatre lampes d'éclairage, 120 V, 100 W, soient branchées à une source de tension de 240 V.
Figure 5-2 Deux groupements série identiques montés en parallèle.
Toutes les lampes ont une tension nominale de 120 V et une puissance nominale de 120 W.
(a) Schéma de câblage; (b) schéma.
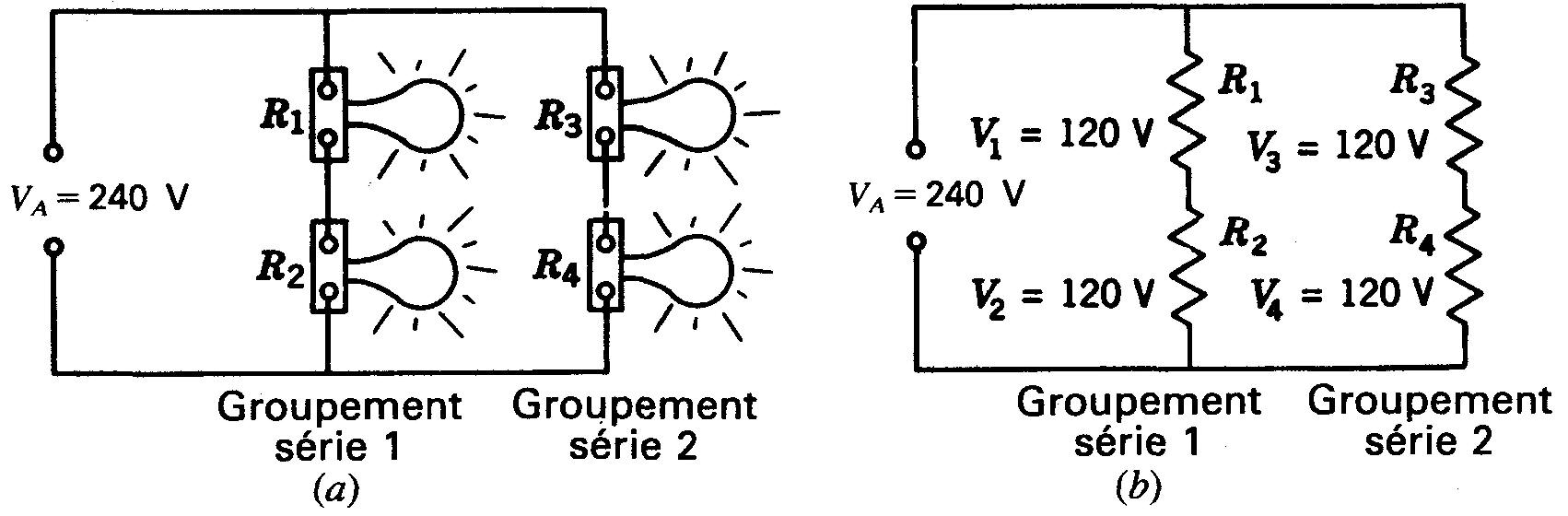
Chaque lampe a besoin de 120 V pour éclairer normalement.
Si les lampes étaient branchées aux bornes de la source, une tension de 240 V serait appliquée à chacune d'elles et ferait circuler dans chaque lampe un courant excessif qui pourrait griller les filaments
Si les quatre lampes étaient montées en série, chacune serait soumise à une différence de potentiel de 60 V, c'est-à-dire le quart de la tension appliquée.
Avec cette tension trop faible, le courant serait insuffisant pour assurer un fonctionnement normal, et les lampes n'éclaireraient pas assez.
Mais, en branchant deux lampes en série aux bornes du secteur 240 V, on obtient 120 V .pour chaque filament, c'est-à-dire la tension nominale de fonctionnement.
Les quatre lampes sont donc branchées en deux groupes de deux lampes montées en série, ces deux groupes série étant branchés en parallèle aux bornes de la source de 240 V.
La tension aux bornes de chaque groupe série est de 240 V. Dans chaque groupe série, deux lampes en série se partagent également la tension appliquée pour appliquer aux filaments les 120 V nécessaires.
La figure 5-3 illustre un autre exemple. Ce circuit ne comprend que deux branches en parallèle; la première branche comprend deux résistances R1 et R2 en série. L'autre branche ne comprend qu'une seule résistance, R3.
On peut appliquer la loi d'Ohm à chaque branche.
Courants de branche I1 et I2 Dans chaque branche, le courant est égal au quotient de la tension appliquée par la résistance totale de cette branche.
Dans la branche 1, Ri et R2 font un total de 12 Ω. On applique 12 V: donc, le courant I1 dans cette branche est de 1 A. Dans la branche 2, I2 est égal à 2 A, puisque la résistance de cette branche est de 6 Ω.
Chutes de tension en série dans une branche
Pour toute résistance d'un jeu de résistances en série, le courant circulant dans l'ensemble multiplié par la valeur de la résistance donne la chute de tension IR, dans cette résistance particulière.
La somme des chutes de tension IR le long de ce jeu de résistances est aussi égale à la tension appliquée aux bornes de l'ensemble.
Dans la branche 1, la chute de tension I1R1 est de 8 V, tandis que la chute de tension I2R2 est de 4 V.
Ces chutes de tension s'additionnent pour former les 12 V appliqués. La tension aux bornes de la branche de R3 est également de 12 V.
Calcul de IT
Le courant total de la ligne principale est la somme des courants dans toutes les branches parallèle. Ici, IT est de 3 A, c'est-à-dire la somme de 1 A pour la branche 1, et de 2 A pour la branche 2.
Calcul de RT
La résistance totale du circuit mixte aux bornes de la source de tension est égale au quotient de la tension appliquée par le courant total de la ligne.
Sur la figure 5-3, RT est égal à 12 V/3 A, soit 4 Cl.
Figure 5-3 Groupement série monté en parallèle avec une autre branche: (a) schéma; (b) circuit équivalent.
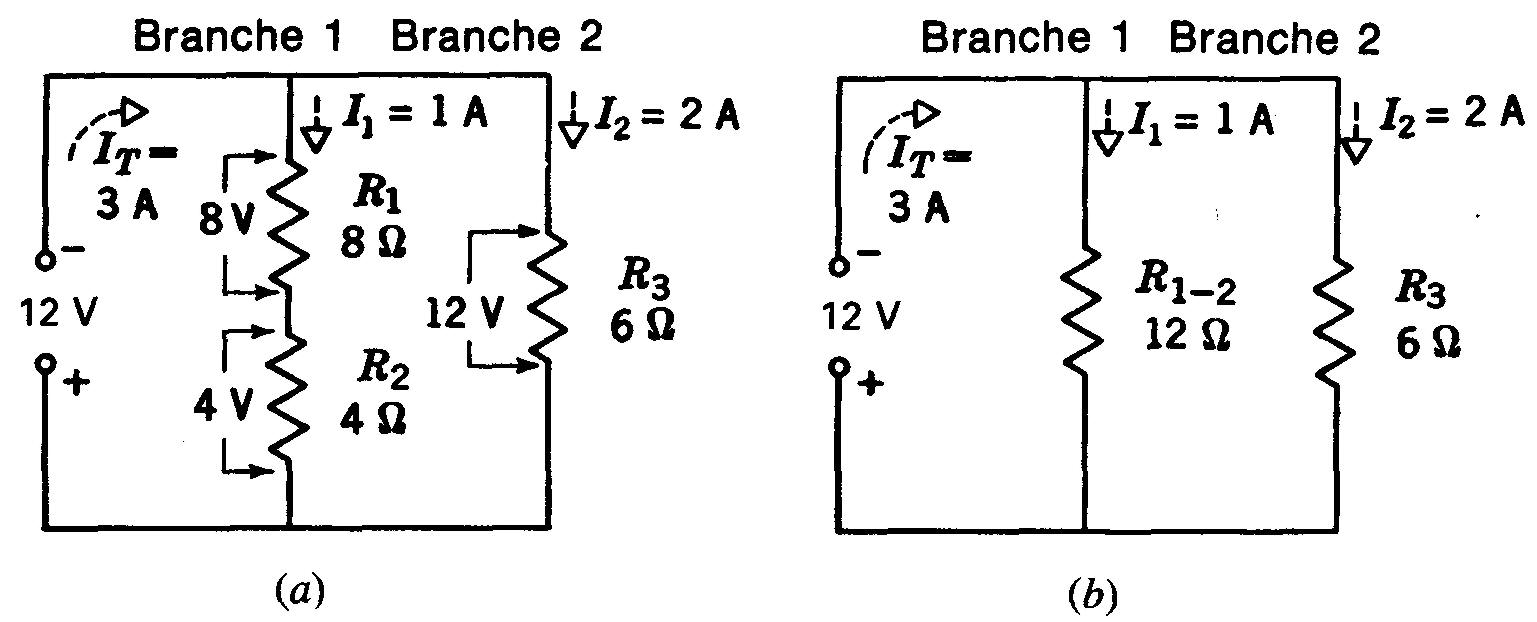
On peut aussi calculer cette résistance comme la combinaison de 12 Ω en parallèle avec 6 Ω, ce qui est équivalent à une résistance combinée de 72 / 18 = 4 Ω, en considérant la formule du produit sur la somme.
Application de la loi d'Ohm
II peut y avoir en parallèle un nombre quelconque de jeux série, et plus de deux résistances en série dans chaque jeu. On peut toujours appliquer la loi d'Ohm de la même manière aux éléments en série et en parallèle du circuit.
Les parties en série ont le même courant.
Les parties en parallèle la même tension.
Se rappeler que dans la formule V/R, la valeur R doit inclure toute la résistance entre les bornes d'application de V.
Problèmes pratiques 5.2 (réponses à la fin du chapitre) Considérer la figure 5-3a:
(a) Si le courant dans R2 était de 6 A, quel courant circulerait dans R1 ?
(b) Si la tension de la source était de 72 V, quelle serait la tension V3 aux bornes de R3 ?
5.3 JEUX DE RÉSISTANCES EN PARALLÈLE MONTÉS EN SÉRIE
Sur la figure 5-4a, le groupement des résistances R2 et R3 en parallèle est appelé un jeu de résistances en parallèle. Ce jeu de résistances est en série avec Ri car tout le courant traversant le jeu de résistances doit traverser R1.
Figure 5-4 Groupement parallèle de R2 et de R3, en série avec R1. (a) schéma; (b) circuit équivalent.
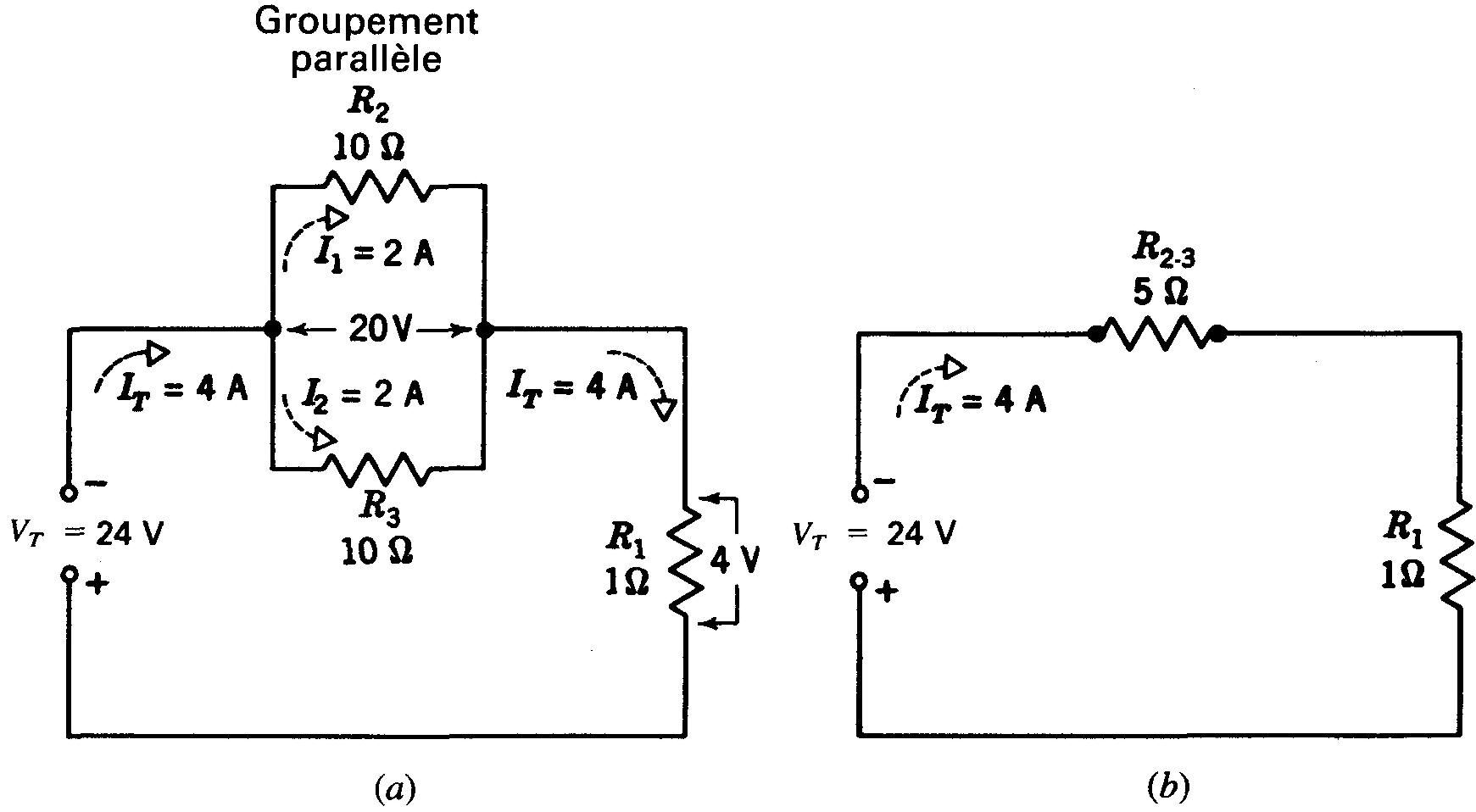
Ce circuit permet de brancher R2 et R3 en parallèle pour que ces deux résistances aient la même différence de potentiel de 20 V à leurs bornes. La source délivre 24 V, mais il y a une chute de tension de 4 V dans R1.
Les deux chutes de tension en série, 4 V dans R1 et 20 V dans le jeu de résistances en parallèle, s'additionnent pour former la tension appliquée de 24 V.
Un tel circuit a pour but d'appliquer la même tension à deux résistances ou plus d'un jeu de résistances en parallèle, quand la tension aux bornes de ce jeu de résistances doit être inférieure à la tension appliquée d'une quantité égale à la chute de tension IR dans une résistance en série.
Pour trouver la résistance de tout le circuit, on doit combiner les résistances en parallèle dans chaque jeu, puis ajouter la résistance en série.
Comme l'indique la figure 5-4b, les deux résistances R2 et R3 de 10 Ω chacune, montées en parallèle, sont équivalentes à 5 Ω.
Puisque la résistance de 5 Ω équivalente aux résistances en parallèle est en série avec la résistance R1 de 1 Ω, la résistance totale de 6 Ω se trouve aux bornes de la source de 24 V. Le courant dans la ligne principale est de 24 V/6 Ω, soit 4 A.
Le courant total de 4 A dans la ligne se partage en deux courants de 2 A circulant dans chacune des résistances en parallèle R2 et R3.
Remarquer que chaque courant partiel est égal à la tension aux bornes du jeu de résistances en parallèle divisée par la résistance de chaque branche. Pour ce jeu, I de chaque branche = 20/10 = 2A.
Les courants partiels se combinent pour former les 4 A qui circulent dans R1. C'est le même courant total qui circule dans la ligne principale et la source, qui arrive au jeu de résistances et qui sort de ce jeu de résistances.
Il peut y avoir plus de deux résistances dans un jeu de résistances en parallèle et un nombre quelconque de jeux de résistances en série.
La loi d'Ohm peut toujours s'appliquer de la même manière aux composants du circuit mixte. La méthode générale applicable aux circuits de ce type consiste à trouver la résistance équivalente à chaque jeu de résistances en parallèle et d'ajouter ensuite toutes les résistances en série.
Problèmes pratiques 5.3 (réponses à la fin du chapitre)
Considérer la figure 5-4a:
(a) Si la tension V2 aux bornes de R2 était de 40 V, quelle serait la tension V3 aux bornes de R3?
(b) Si le courant circulant dans R2 était de 4 A, pour un courant dans R3 de 4 A, quel serait le courant dans R1.
5.4 JEUX DE RÉSISTANCES EN PARALLÈLE ET EN SÉRIE EN MONTAGE MIXTE
Pour trouver la solution de ces circuits, le plus important est de savoir quels sont les composants connectés en série et quels sont les composants du circuit qui forment des branches en parallèle.
Les composants en série doivent constituer un passage unique pour le courant sans aucun noeud. Un noeud comme le point A ou B de la figure 5-5 est commun à deux passages de courant ou plus.
Figure 5-5 Réduction d'un circuit mixte en un circuit série équivalent, pour trouver RT:
(a) circuit réel; (b) R3 et R4 en parallèle équivalent à R7;
(c) R7 et R6 en série équivalent à R13; (d) R13 et R5 en parallèle équivalent à R18;
e) R18, R1 et R2 en série s'additionnent pour former une résistance totale du circuit égale à 50 Ω.
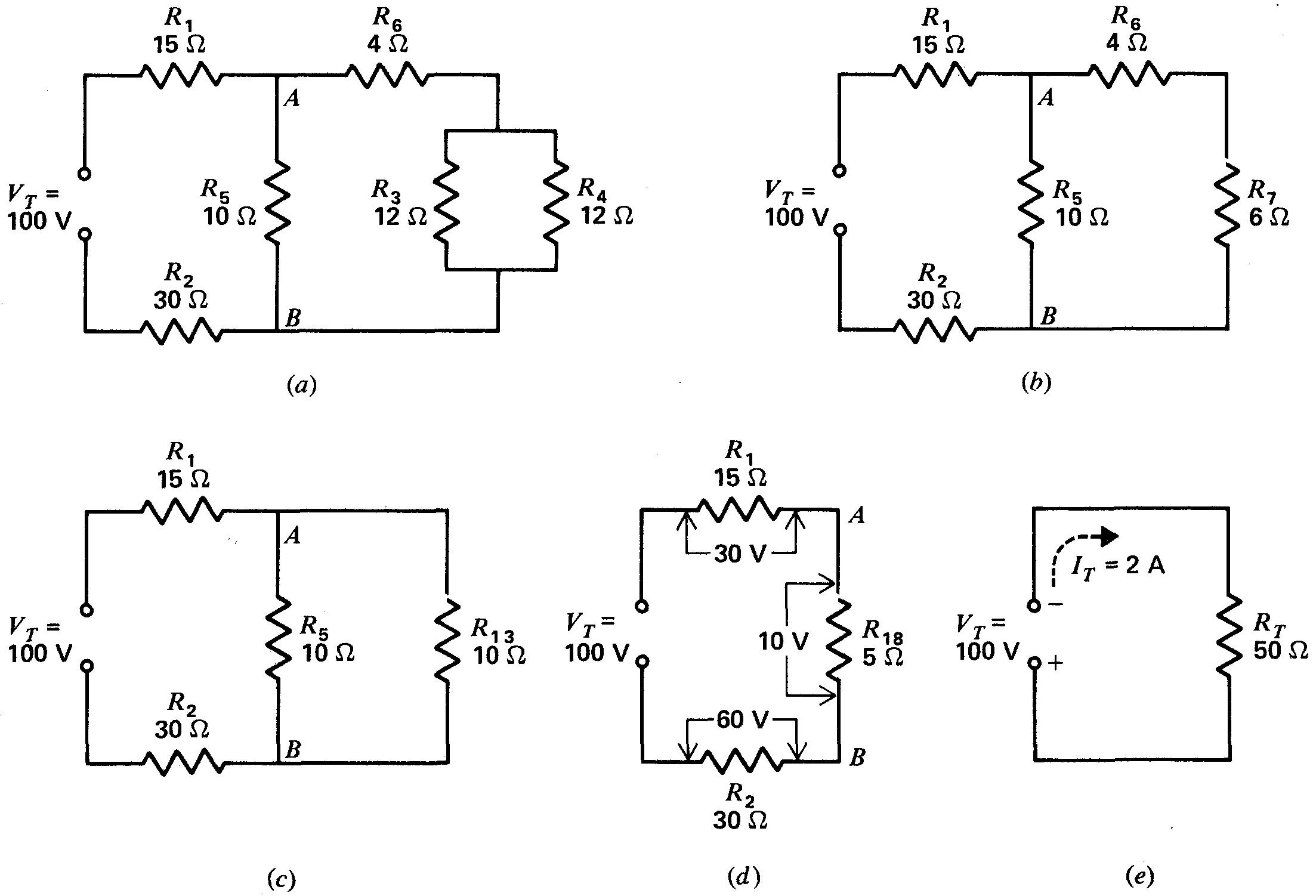
Par exemple, R1 et R6 ne sont pas en série. Ces résistances ne sont pas parcourues par le même courant, puisque le courant circulant dans R1 se partage, au point A, en deux courants de branche. De même, R5 n'est pas en série avec R2, à cause du noeud B.
Pour trouver les courants et les tensions de la figure 5-5, il faut d'abord trouver RT pour calculer le courant IT circulant dans la ligne principale, égal à VT/RT.
Pour calculer RT, il faut commencer par réduire la branche la plus éloignée de la source et travailler en se rapprochant de la source appliquée.
On opère ainsi parce qu'on ne peut pas dire quelle est la résistance en série avec R1 et R2 avant d'avoir réduit les branches en parallèle à leur résistance équivalente.
S'il n'y a pas de source représentée, on peut encore calculer RT en procédant de l'extérieur vers les bornes ouvertes entre lesquelles une source pourrait être branchée.
Pour calculer RT, sur la figure 5-5, les opérations à faire sont les suivantes:
1. En (a), l'ensemble des résistances en parallèle R3 de 12 Ω et R4 de 12 Ω est équivalent à la résistance R7 de 6 Ω, en (b).
2. Les résistances R7 de 6 Ω et R6 de 4 Ω, en série sur le même passage de courant, font au total une résistance R13 de 10 Ω, en (c).
3. La résistance R13 de 10 Ω est en parallèle avec la résistance R5 de 10 Ω, entre les noeuds A et B. Leur résistance équivalente est donc la résistance R18 de 5 Ω en (d).
4. Le circuit (d) ne comprend plus que les résistances en série:
R1 de 15 Ω, Ri8 de 5 Ω et R2 de 30 Ω. Ces résistances font un RT de 50 Ω, comme l'indique la figure 5-5 (e).
5. La résistance RT de 50 Ω est branchée aux bornes de la source de 100 V, le courant IT dans la ligne est donc de 2 A.
Pour obtenir les courants et les tensions individuels, nous pouvons partir du courant IT de 2 A et du circuit équivalent (d). Nous pouvons oeuvrer maintenant en partant de la tension V de la source vers les branches.
Et ce, parce que IT peut servir au calcul des chutes de tension dans la ligne principale. Les chutes de tension IR sont, dans ce cas, les suivantes:
V1 = ITR1 = 2 x 15 = 30 V
V18 = ITR18 = 2 x 5 = 10 V
V2 = ITR2 = 2 x 30 = 60 V
La chute de tension de 10 V aux bornes de R18 est la différence de potentiel réelle entre les noeuds A et B. Ceci signifie qu'il y a 10 V aux bornes de R5 et de R13 en (c).
Les 10 V créent un courant de 1 A dans la branche de R5 de 10 Ω. Les mêmes 10 V sont aussi appliqués à la branche de R13.
Il faut se rappeler que la branche de R13 résulte de la mise en série du jeu de résistances en série R6 et du jeu de résistances en parallèle R3 R4.
Puisque la résistance équivalente à cette branche est de 10 V et que la tension à ses bornes est de 10 V, le courant qui y circule est de 1 A.
Ce courant de 1 A, circulant dans la résistance R6 de 4 Ω, produit une chute de tension de 4 V. La chute de tension IR de 6 V restante est aux bornes du jeu de résistances R3R4.
Les 6 V aux bornes de la résistance R3 de 12 Ω font circuler un courant de 0,5 A dans cette résistance; le courant dans R4 est aussi de 0,5 A.
En suivant tous les trajets du courant depuis la source, on voit que le courant est de 2 A, au travers de R1 sur la ligne principale.
Au noeud A, ce courant se partage en 1 A pour R5 et 1 A pour le montage série contenant R6. Il y a un courant de 1 A dans R6 qui se partage en 0,5 A dans R3 et 0,5 A dans R4.
Au noeud B, le courant total du jeu de résistances en parallèle, soit 1 A, se combine avec le courant de 1 A qui traverse la branche de R5 pour former le courant total de ligne de 2 A qui traverse R2, c'est-à-dire le même courant que celui de R1, du côté opposé de la ligne.
Problèmes pratiques 5.4 (réponses à la fin du chapitre) Considérer la figure 5-5a:
(a) Quelle résistance est en série avec R2?
(b) Quelle résistance est en parallèle avec R3?
(c) Quelle résistance est en série avec le jeu R3R4?
5.5 ANALYSE DES CIRCUITS MIXTES
Nous allons maintenant étudier les circuits des figures 5-6 à 5-10 en illustrant les principes suivants:
1. Lorsque des jeux de résistances en série sont en parallèle sur la ligne principale, on peut trouver les courants individuels ainsi que IT sans connaître RT (voir les figures 5-6 et 5-7).
2. Lorsque des jeux de résistance en parallèle ont des résistances en série avec la ligne principale, il faut calculer RT pour trouver IT en supposant tous les courants de branche inconnus (voir la figure 5-9).
3. La tension de la source est appliquée aux bornes de la résistance RT, équivalente à tout le circuit, et produit un courant IT qui ne circule que dans la ligne principale.
4. Toute résistance en série individuelle a sa propre chute de tension IR qui doit être inférieure à la tension totale VT. De plus, tout courant individuel circulant dans une dérivation doit être inférieur à IT.
Solution de la figure 5-6
Le problème consiste ici à calculer les courants de branche I1 et I2-3» Ie courant total IT et les chutes de tension V1, V2 et V3.
Figure 5-6 Trouvez tous les courants et toutes les tensions. Voir dans le texte la solution en calculant d'abord les courants des différentes branches.
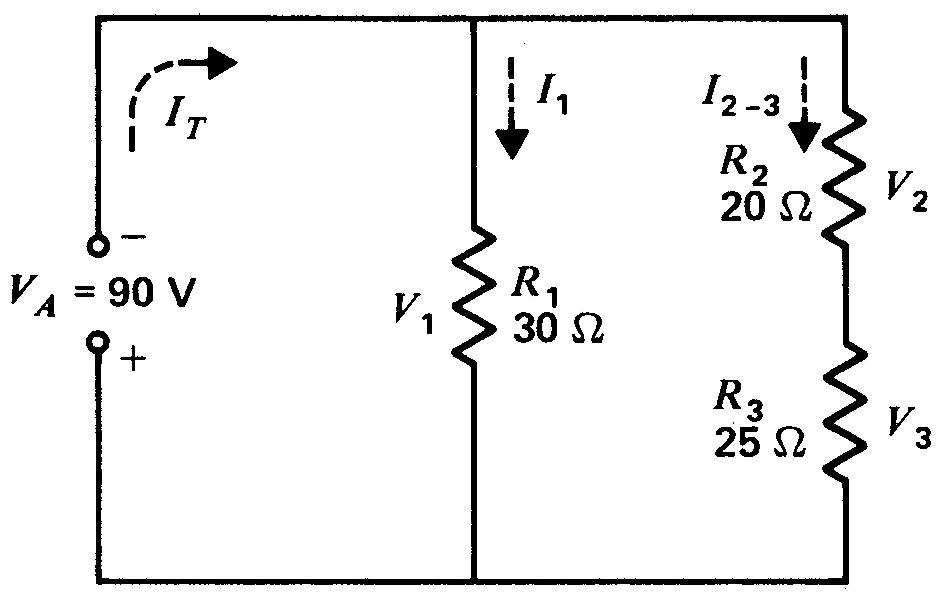
Nous allons suivre l'ordre précédent dans les calculs, puisque l'on peut trouver les courants de branche à partir de la tension de 90 V appliquée aux bornes des branches formées des résistances connues.
Dans la branche R1 de 30 Ω, le courant de branche est de 90 V / 30 Ω, soit I1 = 3 A.
L'autre branche a une résistance totale de 20 Ω pour R2 plus 25 Ω pour R3, soit 45 Ω.
Le courant I2_3 est donc de 90 V / 45 Ω, c'est-à-dire 2 A.
Le courant IT dans la ligne principale est donc de 3 A + 2 A, soit 5 A.
En ce qui concerne les tensions aux bornes des branches, V1 doit être égal à VA c'est-à-dire 90 V.
Ou encore V1 = I1R1, c'est-à-dire 3 x 30 = 90 V.
Dans l'autre branche, le courant I2-3 de 2 A circule dans la résistance R2 de 20 Ω et la résistance R3 de 25 Ω.
Par conséquent, V2 est de 2 x 20 = 40 V et V3 est de 2 x 25 = 50 V.
Remarquer que ces chutes de tension IR en série de 40 V et de 50 V dans une branche font au total 90 V, soit la tension de la source.
Nous pouvons calculer RT comme le quotient de VA par IT, ou 90 V / 5 A, soit 18 Ω.
On peut aussi calculer RT en combinant les résistances des deux branches en parallèle, soit 30 Ω et 45 Ω.
On a alors RT = (30 x 45/30 + 45). La réponse est 1350 / 75, c'est-à-dire les 18 Ω trouvés pour RT.
Solution de la figure 5-7
Figure 5-7 Trouvez VA, V4 et R4. Voir la solution dans le texte par le calcul de I2 et de la tension aux bornes des branches en parallèle.
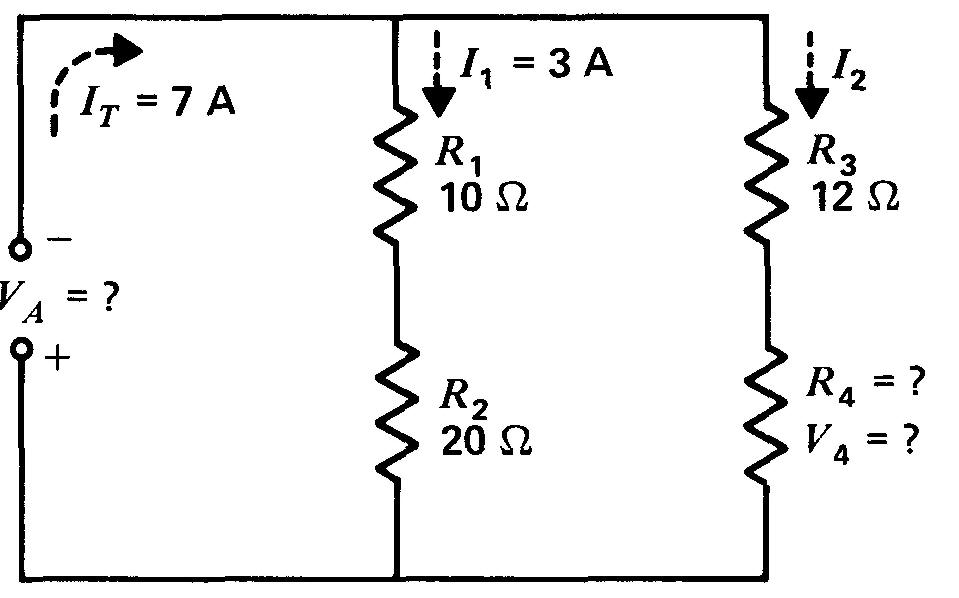
Pour trouver la tension appliquée d'abord, le courant partiel I1 est connu.
Ce courant de 3 A circulant dans la résistance R1 de 10 Ω crée une chute de tension V1 de 30 V dans R1.
Ce même courant de 3 A crée une tension V2 de 60 V dans la résistance R2 de 20 Ω.
Les chutes de tensions de 30 V et de 60 V sont en série aux bornes de la tension appliquée.
Par conséquent, VA est égal à la somme de 30 + 60, ou 90 V.
Ces 90 V sont aussi appliqués aux bornes de l'autre branche comprenant R3 et R4, en série.
Le courant I2 dans la seconde branche de la figure 5-7 doit être égal à 4 A, c'est-à-dire au courant IT de 7 A moins le courant I1 de 3 A.
Avec un courant I2 de 4 A, la chute de tension dans la résistance R3 de 12 Ω est de 48 V pour V3.
La tension aux bornes de R4, étant donné que la somme de V3 et V4 doit être égale aux 90 V appliqués, est donc de 90 - 48, soit 42 V pour V4.
Finalement, avec 42 V aux bornes de R4 et un courant de 4 A dans cette résistance, R4 est de 42/4, soit 10,5 Ω.
Remarquer que 10,5 Ω pour R4, ajoutés aux 12 Ω de R3, font un total de 22,5 Ω qui laissent passer un courant I2 de branche de 90/22,5 ou 4 A.
Solution de la figure 5-8
Figure 5-8 Trouvez R2 et I2. Voir la solution dans le texte.
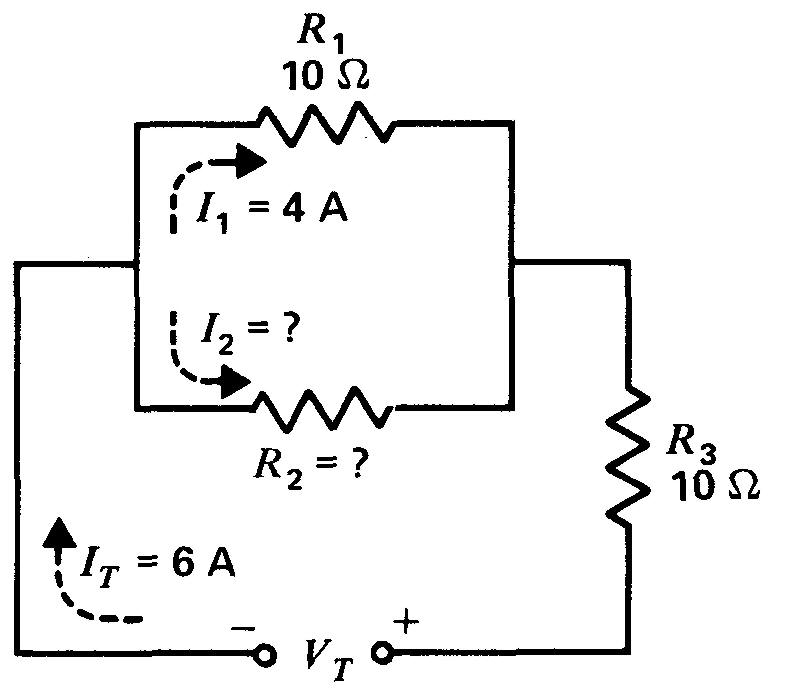
La séparation en courants de branche s'applique aussi à la figure 5-8, mais, dans ce cas, le principe fondamental est que la tension doit être la même aux bornes des résistances parallèle R1 et R2.
Parmi les courants partiels, I2 est de 2 A, c'est-à-dire égal au courant total IT de 6 A moins le courant I1 de 4 A.
La tension aux bornes de la résistance R1 de 10 Ω est de 4 x 10, soit 40 V.
Cette même tension se trouve aussi aux bornes de R2.
La tension aux bornes de R2 étant de 40 V et le courant I2 de 2 A, R2 est de 40/2, soit 20 Ω.
En calculant VT, sur la figure 5-8, on obtient 100 V.
Le courant IT de 6 A produit dans la résistance R3 de 10 Ω une chute de tension V3 de 60 V.
Comme la tension aux bornes des deux résistances en parallèle Ri et R2 a été calculée égale à 40 V, ces 40 V en série avec les 6 V aux bornes de R3 font au total 100 V pour la tension appliquée.
Solution de la figure 5-9
Figure 5-9 Trouvez tous les courants et toutes les tensions. Voir dans le texte la solution par le calcul de RT, puis de IT pour trouver V6 d'abord.
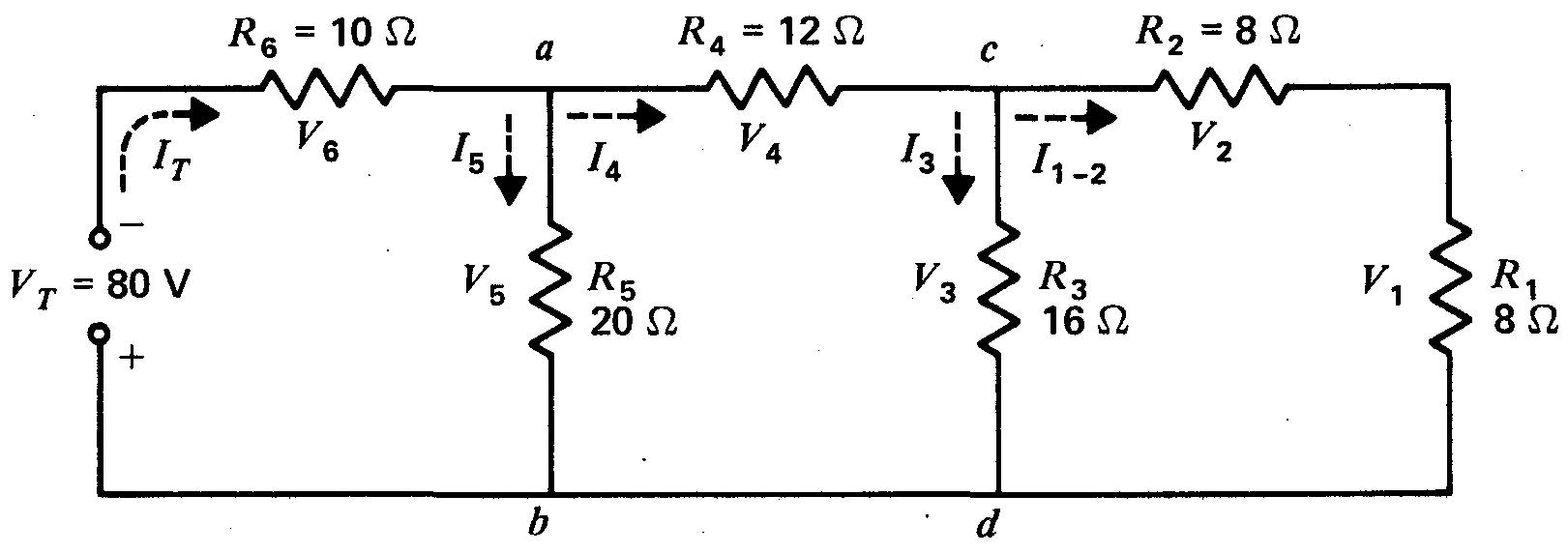
Pour calculer tous les courants et toutes les chutes de tension, il faut connaître RT de manière à obtenir le courant IT traversant R6 sur la ligne principale.
Pour obtenir RT, on commence par combiner R1 et R2 et on progresse vers la source.
On ajoute les 8 Ω de R1 et les 8 Ω de R2 pour obtenir la résistance série de 16 Ω.
Ces 16 Ω en parallèle avec la résistance R3 de 16 Ω ont une résistance équivalente de 8 Ω entre les points c et d.
En ajoutant ces 8 Ω en série avec la résistance R4 de 12 Ω, on obtient 20 Ω.
Ces 20 Ω en parallèle avec la résistance R5 de 20 Ω sont équivalents à 10 Ω entre les points a et b.
On ajoute ces 10 Ω en série avec la résistance R6 de 10 Ω pour obtenir une résistance totale RT du circuit mixte de 20 Ω.
Sur la ligne principale, le courant IT est de VT/RT ou 80/20 c'est-à-dire 4 A. Ce courant IT de 4 A circule dans la résistance R6 de 10 Ω en créant une chute de tension V6 de 40 V.
Maintenant que nous connaissons IT et V6, pour la ligne principale, nous utilisons ces valeurs pour calculer toutes les autres tensions et tous les autres courants.
Nous commençons alors par la ligne principale dont nous connaissons le courant et nous progressons, à partir de la source. Pour trouver V5, on retranche la chute de tension IR, V6 de 40 V dans la ligne principale, de la tension de la source.
En effet, V5 et V6 doivent s'additionner pour former les 80 V de VT.
Donc, V5 est de 80 - 40, soit 40 V.
Ces tensions V5 et V6 sont dans ce cas égales puisqu'elles divisent les 80 V en deux parties égales, car la résistance R6 de 10 Ω est égale à la résistance équivalente de 10 Ω entre les points a et b.
Connaissant la tension V5 de 40 V aux bornes de la résistance R5 de 20 Ω, le courant I5 est de 40/20 = 2 A.
Puisque I5 est de 2 A et IT de 4 A, I4 doit être égal à 2 A représentant la différence entre IT et I5.
Au noeud a, le courant IT de 4 A se divise entre 2 A dans R5 et 2 A dans R4.
Le courant I4 de 2 A produit dans la résistance R4 de 12 Ω une chute de tension IR, V4, égale à 2 x 12 = 24 V.
Il faut remarquer maintenant que V4 et V3 doivent s'additionner pour former V5.
En effet, V5 et l'ensemble V4 et V3 sont égaux à la tension entre les deux points ab ou ad. Puisque la différence de potentiel entre deux points est la même, quel que soit le trajet suivi, V5 = V4 + V3.
Pour trouver V3, on peut maintenant retrancher les 24 V de V4 des 40 V de V5. Donc, V3 est de 40 - 24 = 16 V.
La tension V3 étant de 16 V aux bornes de R3 qui est de 16 Ω, le courant 73 est de 1 A.
Le courant I1-2 dans la branche contenant R1 et R2 est aussi de 1 A. Le courant I4 de 2 A se partage au noeud c en deux courants partiels égaux à 1 A chacun puisque les résistances des deux branches sont égales.
Enfin, le courant qui circule dans la résistance R2 de 8 Ω et dans la résistance R1 de 8 Ω étant de 1 A, les chutes de tension V2 et V1 sont toutes deux de 8 V.
Remarquez que la tension V1 de 8 V s'ajoute à la tension V2 de 8 V, en série, pour former la différence de potentiel V3 de 16 V, entre les points c et d.
Toutes les réponses au problème de la figure 5-9 sont rassemblées ci-dessous:
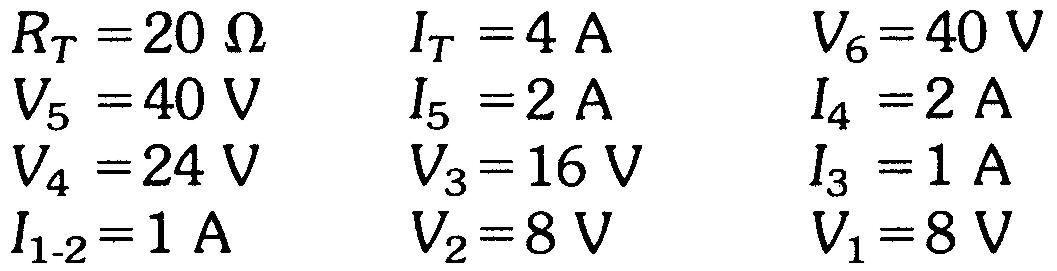
Problèmes pratiques 5.5 (réponses à la fin du chapitre)
(a) Soit la figure 5-6. Quelle résistance est en série avec R2?
(b) Soit la figure 5-6. Quelle résistance est aux bornes de VA?
(c) Soit la figure 5-7. Calculer le courant I2.
(d) Soit la figure 5-8. Calculer la tension V3.
5.6 LE PONT DE WHEATSTONE (Sir Charles Wheatstone (1802-1875), physicien et inventeur anglais.)
Un circuit en pont a quatre bornes: deux pour la tension d'entrée, deux pour la sortie.
Le but d'un tel montage est de réaliser un circuit dans lequel les chutes de tension sont équilibrées, si bien que la tension de sortie est nulle, alors qu'une tension est appliquée à l'entrée.
Sur la figure 5-10, les bornes d'entrée sont C et D, tandis que les bornes de sortie sont A et B.
Figure 5-10 Circuit du pont de Wheatstone.
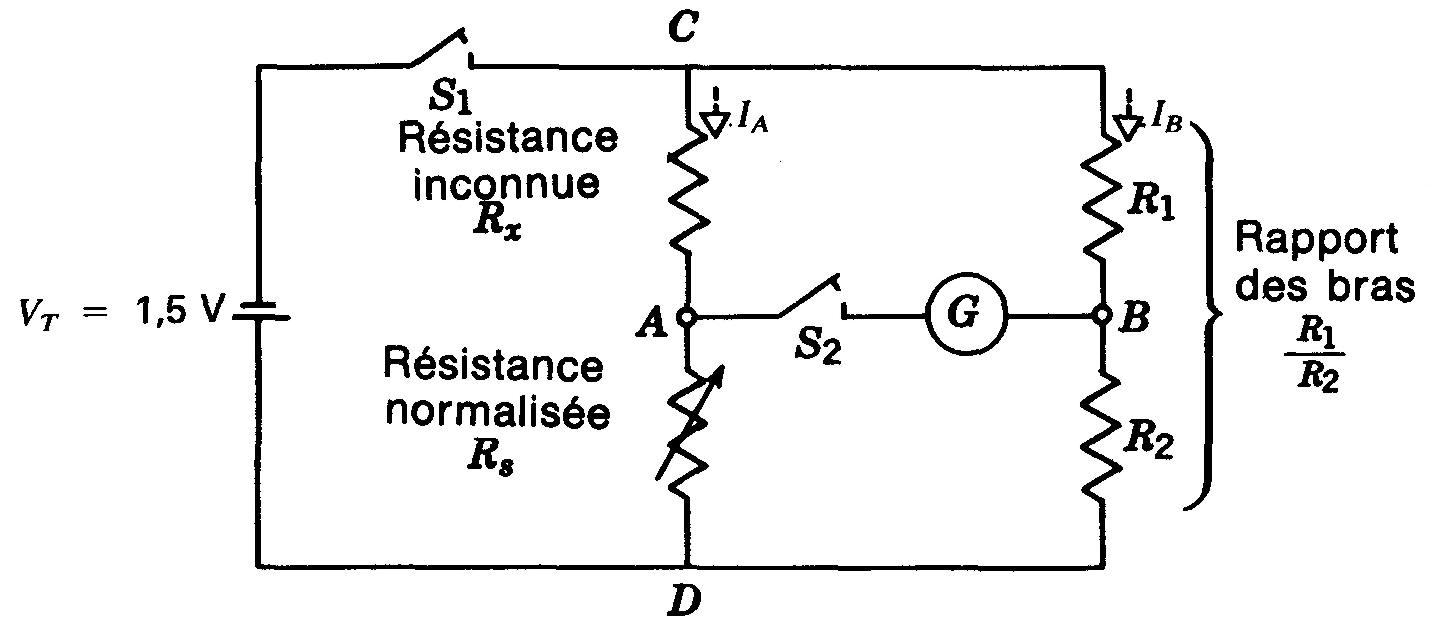
Ce circuit en pont a de nombreuses applications pour les mesures comparatives.
Dans le pont de Wheatstone, une résistance inconnue Rx est équilibrée par une résistance étalon précise R, pour obtenir une mesure précise de la résistance.
Sur la figure 5-10, S1 applique la tension de la pile aux quatre résistances du pont.
Pour équilibrer le pont, on fait varier la valeur de Rs.
On a atteint l'équilibre quand le courant est nul dans le galvanomètre G. L'interrupteur à ressort que l'on ferme seulement pour vérifier l'indication du galvanomètre est représenté par S2.
On comprend pourquoi le courant est nul dans le galvanomètre en analysant les chutes de tension dans les résistances. La résistance Rs, en série avec Rx, forme un diviseur de tension aux bornes de VT; l'ensemble parallèle des résistances en série R1 et R2 forme aussi un diviseur de tension aux bornes de la même source.
Quand les rapports de tension sont les mêmes dans les deux branches en parallèle, la chute de tension dans R, en série avec Rx, forme un diviseur de tension aux bornes de VT; l'ensemble parallèle des résistances en série R1 et R2 forme est égale à la chute de tension dans R2.
Alors la tension aux bornes de Rx est aussi égale à la tension aux bornes de R1.
Dans ce cas, les points A et B doivent être au même potentiel. La différence de potentiel aux bornes de l'appareil de mesure est donc nulle et il n'y a pas de déviation.
A l'équilibre, on peut écrire l'égalité des tensions dans les deux branches du pont de Wheatstone sous la forme:
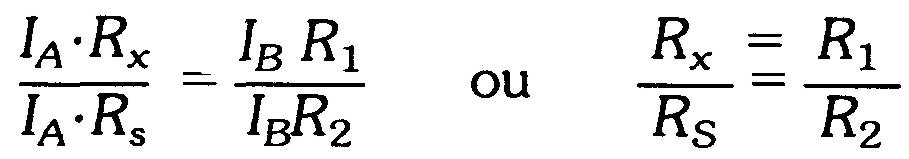
Remarquer que IA et IB s'éliminent. En multipliant par Rs, on obtient:
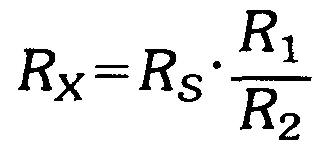 (5.1)
(5.1)
Habituellement, la somme des résistances R1 et R2 est fixe mais on peut choisir un rapport quelconque en déplaçant le point B sur le bras de réglage des rapports.
On équilibre le pont en faisant varier Rs pour obtenir un courant nul dans l'appareil de mesure. A l'équilibre, on peut donc obtenir la valeur de Rx en multipliant Rs par le rapport R1/R2.
Si, par exemple, le rapport est de 1/100 et Rs de 248 Ω, la valeur de Rx est égale à 248 x 0,01, soit 2,48 Ω.
On peut analyser le circuit en pont équilibré comme s'il s'agissait simplement de deux séries de résistances en parallèle, quand le courant est nul dans l'appareil de mesure.
En l'absence de courant entre A et B, tout se passe comme si le trajet correspondant était ouvert.
Mais, quand un courant circule dans le circuit de l'appareil de mesure, il faut analyser le circuit en pont en appliquant les lois de Kirchhoff ou les théorèmes des circuits, comme l'indiquent les chapitres 8 et 9.
Problèmes pratiques 5.6 (réponses à la fin du chapitre)
(a) Un circuit en pont comporte combien de paires de bornes?
(b) Soit la figure 5-10. Que vaut la tension Vas à l'équilibre?
5.7 CONNEXIONS À UNE MASSE COMMUNE
Dans le câblage des circuits usuels, un côté de la source de tension est habituellement mis à la masse.
Dans le cas du câblage domestique, sur le secteur alternatif à 120 V, la masse est en réalité la masse du sol et on réalise une liaison avec une canalisation métallique d'eau froide.
Dans le cas des appareils électroniques, la masse est celle d'un châssis métallique qui sert de retour commun à toutes les liaisons revenant à la source.
Quand le câblage est imprimé sur une plaquette de matière plastique, en remplacement du châssis métallique, un passage conducteur entourant toute la plaquette sert de retour commun.
La masse générale peut ou non être connectée à la masse du sol. Dans l'un ou l'autre cas, le côté mis à la masse est le côté de tension nulle ou côté «bas» de la tension appliquée tandis que le côté qui n'est pas à la masse est le côté sous tension ou côté «haut».
Mise à la masse d'un côté de la source de tension
La figure 5-11 donne trois exemples.
Figure 5-11 Mise à la masse d'un côté d'une source de tension:
(a) ligne d'alimentation en courant alternatif; (b) côté négatif de la batterie relié à la masse générale;
(c) côté positif de la batterie relié à la masse générale.
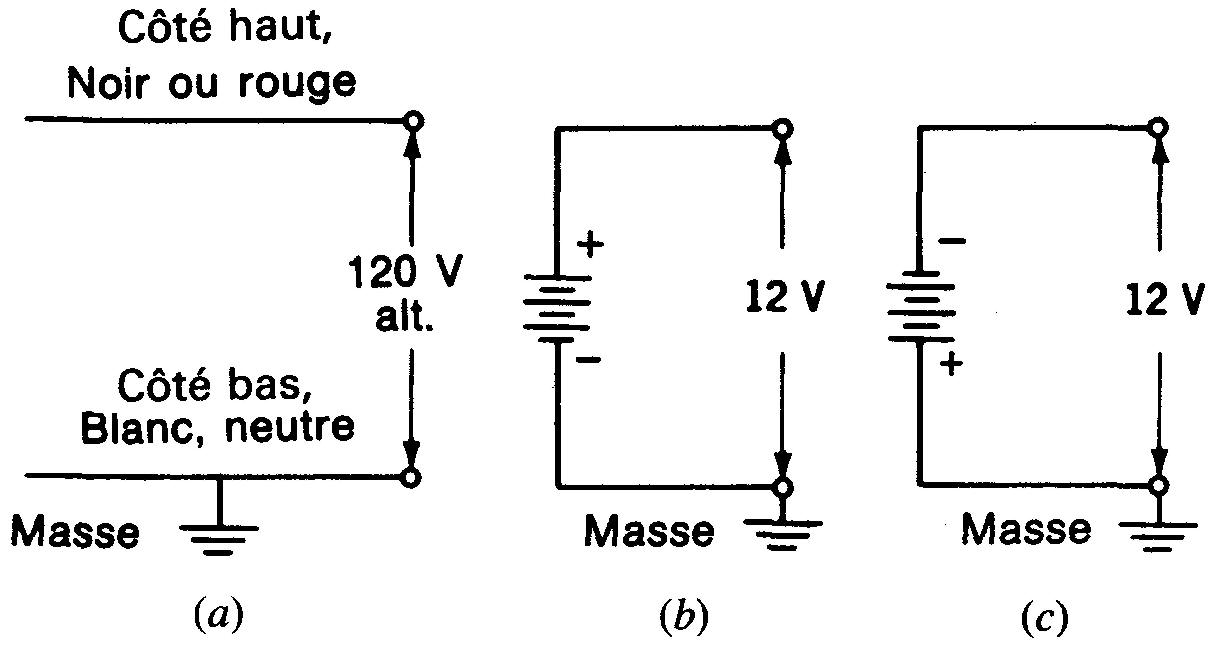
En (a), un côté du secteur
alternatif à 120 V est mis à la masse. Remarquer le symbole
![]() utilisé pour indiquer la masse.
utilisé pour indiquer la masse.
Ce symbole indique aussi une masse générale qui est reliée à un côté de la source de tension.
Dans les appareils électroniques, on utilise généralement un fil noir pour les retours à la masse générale et un fil rouge pour le point haut de la source de tension. Voir le tableau F-1 de l'Annexe F.
Sur les figures 5-11b et c, on utilise la batterie de 12 V comme exemple de source de tension reliée à un châssis de masse mais non reliée à la terre.
Dans une automobile, par exemple, un côté de la batterie est relié au châssis métallique de la voiture.
En (b), le côté négatif est mis à la masse, tandis qu'en (c), le côté positif est mis à la masse. Certaines personnes pensent que la masse doit être négative, mais il n'en est pas nécessairement ainsi.
On connecte un côté du secteur alternatif à 120 V à la masse pour réduire les risques de secousses électriques. Mais, dans un appareil électronique, le châssis de masse est surtout une connexion commune de retour.
Lorsque l'équipement fonctionne à partir du secteur, le châssis métallique devra être au potentiel de la masse et non relié au côté haut de la prise en alternatif.
Cette connexion diminue la possibilité de recevoir des secousses électriques venant du châssis. De plus, le ronflement dû au secteur est réduit dans les équipements audio, radio et de télévision.
Problèmes pratiques 5-7 (réponses à la fin du chapitre)
(a) Soit la figure 5-11b. Donner la valeur et la polarité de la tension par rapport à la masse.
(b) Mêmes questions pour la figure 5-11e.
5.8 TENSIONS MESURÉES PAR RAPPORT À LA MASSE DU CHÂSSIS
Si, dans un circuit, on utilise le châssis comme retour commun, on mesure généralement les tensions par rapport à ce châssis.
Considérons le diviseur de tension de la figure 5-12, sans aucune masse, en (a), puis, analysons l'effet produit par la mise à la masse de différents points du diviseur.
Figure 5-12 Tensions par rapport à la masse générale:
(a) diviseur de tension sans mise à la masse;
(b) le côté négatif de la source VT étant à la masse, toutes les tensions sont positives par rapport à la masse générale;
(c) tensions positives et négatives par rapport à la masse au point B;
(d) le côté positif de la source étant mis à la masse, toutes les tensions sont négatives par rapport à la masse générale.
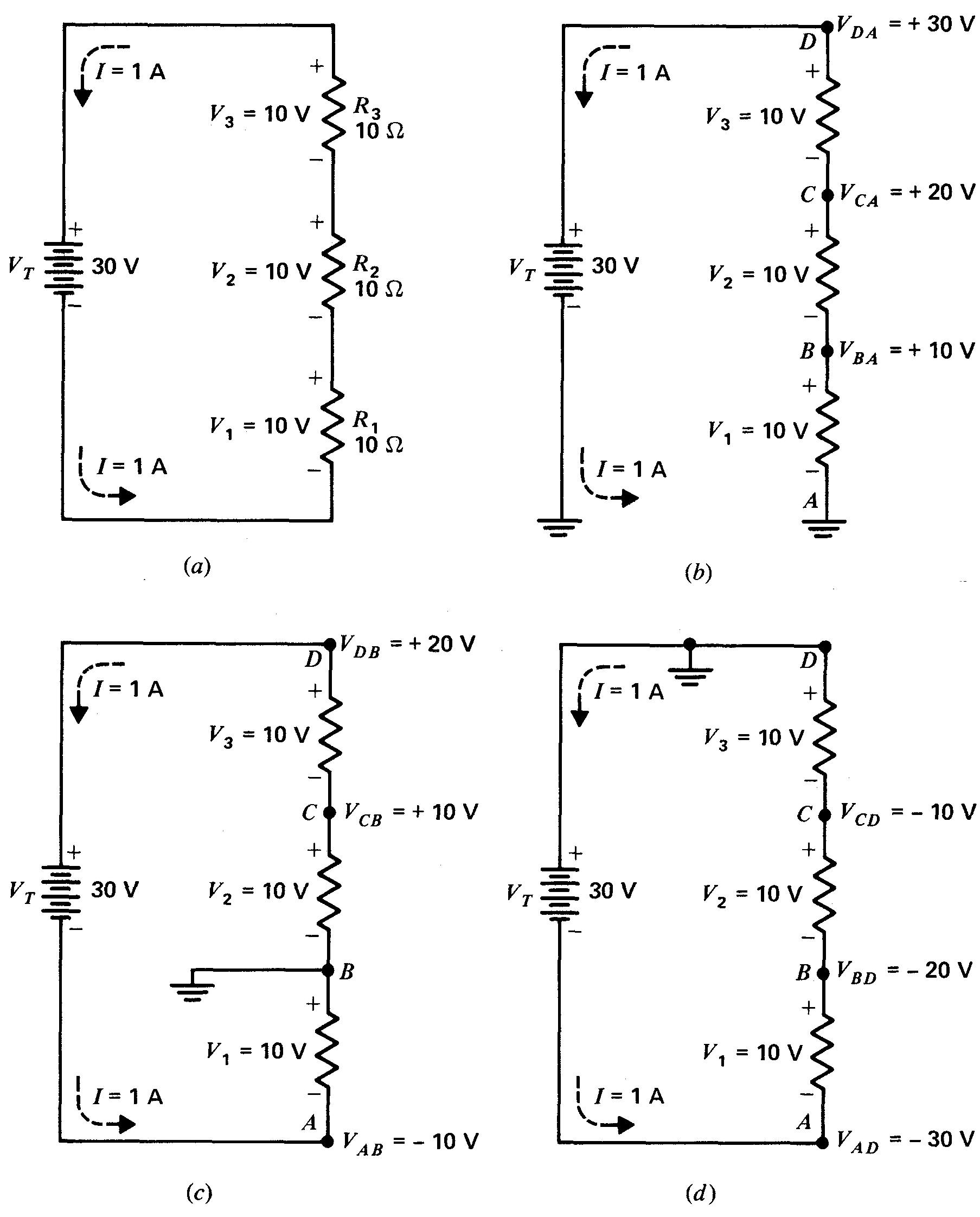
Il est important de comprendre que ce circuit fonctionne de la même manière avec ou sans masse. Seul le point de référence utilisé pour la mesure des tensions varie.
Les trois résistances de 10 Ω, R1, R2, R3 de la figure 5-12a, divisent la tension de la source de 30 V en parties égales. Chaque chute de tension, V1, V2 et V3, est donc égale à 30/3 = 10 V.
La polarité de chaque résistance est positive en haut et négative en bas, de même que la source VT.
Quant au courant I, il est de 30/30 = 1 A. Chaque chute IR est de 1 x 10 = 10 V pour V1, V2 et V3.
Tensions positives par rapport à la masse négative
Sur la figure 5-12b, le côté négatif de VT est mis à la masse et l'extrémité inférieure de R1 est également mise à la masse pour fermer le circuit.
La masse est au point A.
Remarquer que les tensions individuelles V1, V2 et V3 sont toujours de 10 V chacune. Le courant reste aussi égal à 1 A.
La direction est toujours la même, à partir du côté négatif de VT, en passant par le châssis métallique, pour atteindre l'extrémité inférieure de R1.
Le châssis de masse a dans ce cas pour unique effet de constituer un passage conducteur depuis un côté de la source jusqu'à un côté de la charge.
Mais, comme il existe une masse sur la figure 5-12b, il est utile de considérer les tensions par rapport au châssis de masse.
Autrement dit, la masse au point A sera maintenant la référence pour toutes les tensions. Quand on indique la tension pour un point seulement d'un circuit, on suppose, en général, que l'autre point est le châssis de masse.
Il faut deux points pour définir une différence de potentiel.
Considérons les tensions aux points B, C et D.
La tension entre B et la masse est VBA.
Ce double indice montre que nous mesurons 3a tension en B, par rapport à A.
En général, la première lettre désigne le point de mesure et la seconde lettre, le point de référence.
Donc VBA est de +10 V.
Le signe positif est utilisé ici pour préciser la polarité. La valeur de 10 V, pour VBA, est la même que celle de V1 aux bornes de R1 puisque les points B et A coïncident avec les extrémités de R1.
En réalité, V1, tension aux bornes de R1 ne peut, sans point de référence, être accompagnée d'une polarité.
Mais la tension en C est VCA dont la valeur est de +20 V.
Cette tension est égale à V1 + V2, qui sont connectées avec des polarités en conjonction.
Au point D, en haut, VDA est de + 30 V, soit V1 + V2 + V3.
Tensions positives et négatives par rapport à une prise mise à la masse
Sur la figure 5-12c, le point B du diviseur de tension est mis à la masse.
Cette mise à la masse permet au diviseur de délivrer des tensions négatives et positives par rapport au châssis de masse.
Ici, la tension négative est VBA qui est de —10 V.
C'est la même tension V1 de 10 V, mais V1 est la tension à l'extrémité négative A par rapport à l'extrémité positive B.
Les autres tensions du diviseur sont VCB= + 10 V, et VDB = +20 V.
Nous pouvons considérer la masse en B comme le point qui sépare les tensions négatives et les tensions positives.
Pour tous les points se trouvant dans la direction du côté positif de VT, la tension est positive par rapport à la masse; dans l'autre direction, vers le côté négatif de VT, une tension quelconque est négative par rapport à la masse.
Tensions négatives par rapport à une niasse positive
Sur la figure 5-12d, c'est le point D, en haut du diviseur, qui est mis à la masse, ce qui est identique à une mise à la masse du côté positif de la source VT.
Dans ce cas, la tension de la source est inversée par rapport au cas (a), puisque c'est le côté opposé qui est à la masse.
En (d), toutes les tensions du diviseur sont négatives par rapport à la masse.
Dans ce cas, VCD = -10 V, tandis que VBD= -20 V et VAD = -30 V.
Un point quelconque du circuit doit être plus négatif que la borne positive de la source, même si cette borne est à la masse.
Problèmes pratiques 5.8 (réponses à la fin du chapitre)
Considérer la figure 5-12c. Donner la tension et la polarité de:
(a) A par rapport à la masse;
(b) B par rapport à la masse;
(c) D par rapport à la masse;
(d) VDA aux bornes de VT.
5.9 CIRCUITS OUVERTS ET COURTS-CIRCUITS DANS LES CIRCUITS MIXTES
Un court-circuit a une résistance pratiquement nulle. Il a donc pour effet de laisser passer un courant excessif. Un circuit ouvert a l'effet inverse puisqu'il a une résistance infiniment grande ne laissant passer pratiquement aucun courant.
En outre, dans les circuits mixtes, un court-circuit ou un circuit ouvert modifient le circuit des autres résistances.
Par exemple, sur la figure 5-13, le circuit mixte de (a) devient un circuit en série comprenant uniquement R1 quand il y a un court-circuit entre les bornes A et B.
Figure 5-13 Effet d'un court-circuit sur des connexions mixtes:
(a) circuit normal avec Si ouvert; (b) circuit court-circuité entre A et B quand S1 est fermé. R2 et R3 sont en court-circuit.
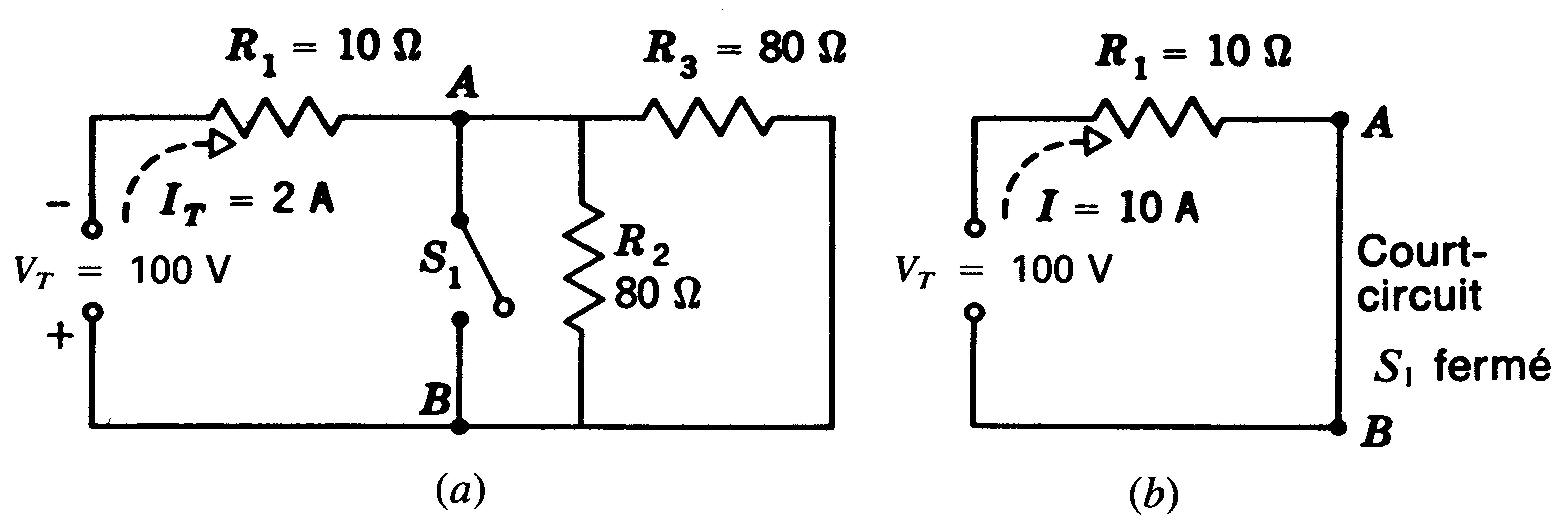
Comme exemple de circuit ouvert, le circuit mixte de la figure 5-14a devient un circuit série comprenant uniquement R1 et R2, quand il y a une coupure entre les bornes C et D.
Effet d'un court-circuit
On peut étudier le circuit mixte de la figure 5-13a pour voir l'influence d'un court-circuit. Quand le circuit est normal et que S1 est ouvert, R2 et R3 sont en parallèle.
Bien que R3 soit dessiné horizontalement, ses deux extrémités coïncident avec celles de R2. Le commutateur S1 ne joue pas ici le rôle d'une branche en parallèle, puisqu'il est ouvert.
La résistance équivalente à la combinaison des résistances R2 de 80 Ω et R3 de 80 Ω en parallèle est de 40 Ω. Cette résistance équivalente de 40 Ω est en série avec la résistance R1 de 10 Ω.
La résistance RT est donc de 40 + 10 = 50 Ω.
Dans la ligne principale, le courant IT est donc de 100/50 = 2A.
La tension V1 aux bornes de la résistance R1 de 10 Ω, dans la ligne principale, est de 2 x 10 = 20 V.
Les 80 V restants se trouvent aux bornes de l'ensemble R2 et R3, en parallèle.
Donc, V2 = 80 V, et V3 = 80V.
Considérons maintenant l'influence de la fermeture du commutateur S1.
Un commutateur fermé a une résistance nulle. Non seulement R2 est court-circuité, mais R3 dans le groupement avec R2 est aussi court-circuité. Le commutateur fermé court-circuite tout ce qui est branché entre les bornes A et B.
Il en résulte un circuit série qui est représenté sur la figure 5-13b.
Dans ce cas, seule la résistance R1 de 10 Ω s'oppose au passage du courant; I est égal à V/R1 c'est-à-dire 100/10 = 10 A. Ce courant de 10 A traverse R1 le commutateur fermé et la source.
Comme R1 est traversé par 10 A au lieu de son courant nominal de 2 A, cet excès de courant peut provoquer un dégagement de chaleur trop important dans R1.
Il ne passe aucun courant dans R1 ni R3 qui sont court-circuités.
Effet d'une coupure de circuit
La figure 5-14a représente le même circuit que la figure 5-13a, mais le commutateur S2 est maintenant utilisé pour brancher R3 en parallèle avec R2.
Figure 5-14 Influence d'une coupure dans un circuit mixte:
(a) circuit normal avec S2 fermé; (b) circuit série avec R1 et R2, quand S2 est ouvert.
Dans la branche coupée, R3 ne reçoit pas de courant et ne crée pas de chute de tension IR.
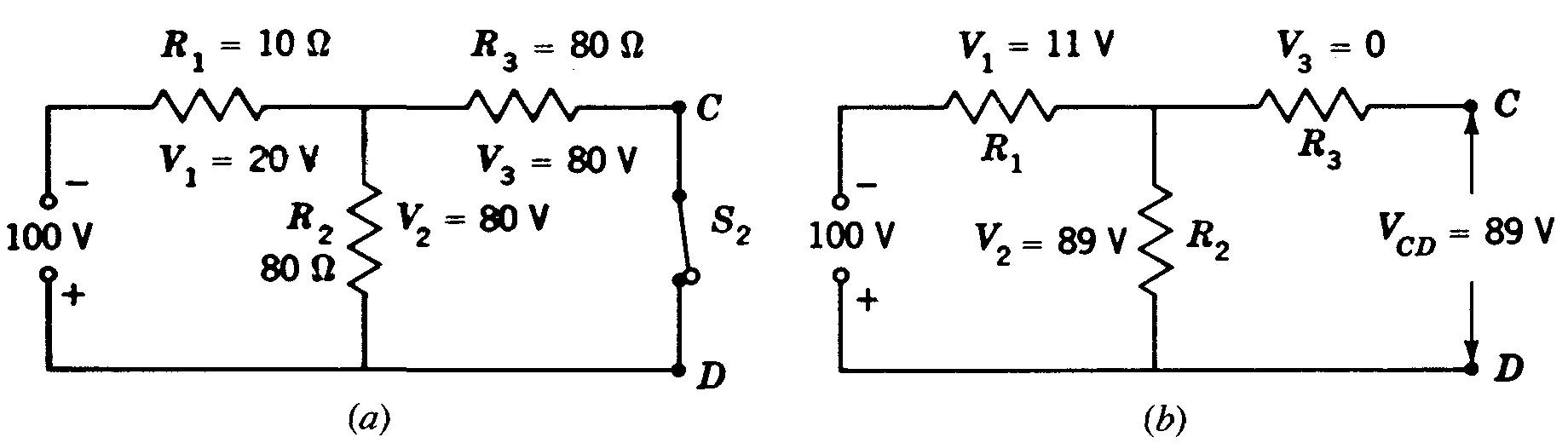
Quand S2 est fermé, en fonctionnement normal, tous les courants et toutes les tensions ont les valeurs calculées pour le circuit mixte.
Mais considérons l'effet de l'ouverture de S2, comme l'indique la figure 5-14b.
Un commutateur ouvert a une résistance infinie. Il y a maintenant une coupure entre les bornes C et D.
En outre, comme R3 se trouve sur le circuit ouvert, on ne peut plus considérer que ses 80 Ω sont en parallèle avec R2.
Le circuit représenté sur la figure 5-14b, avec S2 ouvert, est identique au circuit comprenant uniquement R1 et R2 en série avec la source de 100 V.
La branche ouverte comprenant R3 ne joue pas le rôle d'une branche en parallèle. Cela est dû au fait qu'aucun courant ne circule dans R3.
On peut considérer les deux résistances R1 de 10 Ω et R2 de 80 Ω en série comme un diviseur de tension, dans lequel chaque chute I est proportionnelle à sa résistance.
La résistance série totale R est de 80 + 10 = 90 Ω.
La résistance R1 de 10 Ω est les 10/90, soit 1/9, de la résistance totale R et V1 est égal à 1/9 de la tension appliquée VT; V1 est donc de 1/9 x 100 = 11V, tandis que V2 est de 8/9 x l00 = 89 V environ.
La chute de 11 V pour V1 et celle de 89 V pour V2 s'additionnent pour donner les 100 V de la tension appliquée.
Remarquez que V3 est nul. Comme aucun courant ne traverse R3, il ne peut pas y avoir de chute de tension dans R3.
En outre, la tension entre les bornes C et D qui ne sont pas reliées est égale à V2, soit 89 V.
Comme il n'y a pas de chute de tension aux bornes de R3, la borne C est au même potentiel que la borne supérieure de R2.
La borne D est directement reliée à la borne inférieure de R2. La différence de potentiel entre C et D est donc de 89 V, aux bornes de R2.
Problèmes pratiques 5.9 (réponses à la fin du chapitre)
(a) Soit la figure 5-13. Le court-circuit augmente IT de 2 A à quelle valeur?
(b) Soit la figure 5-14. La branche ouverte réduit IT de 2 A à quelle valeur?
Résumé
1. Le tableau 5-1 résume les principales caractéristiques des circuits série et parallèle. Dans les circuits associant des branchements série et parallèle, les composants qui se trouvent sur le même passage du courant, sans qu'il y ait de noeud, sont en série; les composants du circuit, connectés entre les deux mêmes noeuds, sont en parallèle.
Tableau 5-1 Comparaison entre les circuits série et les circuits parallèle

2. Pour calculer RT dans un circuit mixte comprenant R dans la ligne principale, combiner les résistances depuis l'extérieur, en revenant vers la source.
3. On utilise couramment un châssis servant de masse comme liaison de retour vers un côté de la source de tension. Les tensions mesurées par rapport au châssis de masse peuvent avoir soit une polarité négative, soit une polarité positive.
4. Quand le potentiel est le même aux deux extrémités d'une résistance, la chute de tension dans cette résistance est nulle. Ou encore, si aucun courant ne circule dans une résistance, il ne peut pas y avoir de chute de tension IR dans cette résistance.
Exercices de contrôle
(Réponses aux exercices de contrôle)
Voici un moyen de contrôler si vous avez bien assimilé le contenu de ce chapitre. Ces exercices sont uniquement destinés à vous évaluer vous-même.
Choisir (a), (b), (c) ou (d).
1. Dans le circuit mixte de la figure 5-1b:
a) R1 est en série avec R3; (b) R2 est en série avec R3; (c) R4 est en parallèle avec R3; (d) R1 est en parallèle avec R3.
2. Dans le circuit mixte de la figure 5-2b:
(a) R1 est en parallèle avec R3; (b) R2 est en parallèle avec R4; (c) R1 est en série avec R2; (d) R2 est en série avec R4.
3. Dans le circuit mixte de la figure 5-5, le total des courants individuels de toutes les branches arrivant au noeud A et sortant du noeud B est de:
(a) 0,5 A; (b) 1 A; (c) 2 A; (d) 4 A.
4. Dans le circuit de la figure 5-2 comprenant quatre lampes d'éclairage de 120 V, 100 W, la résistance de chaque lampe est de:
(a) 72 Ω; (b) 100 Ω; (c) 144 Ω; (d) 120 Ω
5. Dans le circuit mixte de la figure 5-4a:
(a) R2 est en série avec R3;
(b) R1 est en série avec R3;
(c) la résistance équivalente à R2R3 est en parallèle avec R1,
(d) la résistance équivalente à R2R3 est en série avec R1
6. Dans un circuit série à résistances inégales:
(a) la plus grande tension est aux bornes de la plus faible résistance;
(b) la plus grande tension est aux bornes de la plus grande résistance;
(c) le plus grand courant parcourt la plus petite résistance;
(d) le plus grand courant parcourt la plus grande résistance.
7. Dans un circuit parallèle à branches de résistances inégales:
(a) le courant le plus élevé circule dans la plus grande résistance;
(b) le courant est le même dans toutes les branches;
(c) la tension est la plus élevée aux bornes de la résistance la plus faible;
(d) le courant est le plus élevé dans la résistance la plus faible.
8. Sur la figure 5-14, quand S2 est ouvert, RT est égal à:
(a) 90 Ω; (b) 100 Ω; (c) 50 Ω, (d) 10 Ω.
9. Sur la figure 5-12c, VDA est égal à:
(a) +10 V; (b) -20 V; (c)-30V; (d) +30V.
10. Dans le pont de Wheatstone de la figure 5-10, à l'équilibre:
(a) IA = 0; (b) IB = 0; (c) V2 = 0; (d) VAB = 0.
Questions
1. Dans un circuit mixte, comment pouvez-vous trouver quelles sont les résistances en série et les résistances en parallèle?
2. Dessinez le schéma de deux résistances en parallèle, placées en série avec une autre résistance.
3. Dessinez un schéma montrant comment relier trois résistances de valeurs égales pour que la résistance équivalente à. l'ensemble soit une fois et demie la résistance de l'une d'elles.
4. Dessinez un schéma représentant deux circuits série en parallèle aux bornes d'une source de tension, chaque circuit série comprenant trois résistances.
5. Expliquez pourquoi des composants sont connectés en montage mixte, en donnant un circuit comme exemple à vos explications.
6. Indiquez deux différences entre un court-circuit et une coupure de circuit.
7. Indiquez la différence entre un diviseur de tension et un diviseur de courant.
8. Donnez un exemple dans lequel une tension est négative par rapport à la masse du châssis.
9. Dessinez un circuit comprenant neuf lampes d'éclairage de 40 V, 100 W, branchées à une source de 120 V.
10. (a) Deux résistances de 10 Ω sont en série avec une source de 100 V. Si on ajoute une troisième résistance de 10 Ω en série, expliquez pourquoi I diminue,
(b) Les deux mêmes résistances de 10 Ω sont en parallèle avec une tension de 100 V. Si on ajoute une troisième résistance R de 10 Ω, en parallèle, expliquez pourquoi IT augmente.
Problèmes
(Réponses aux problèmes de numéro impair)
1. En vous reportant à la figure 5-1:
(a) calculez la résistance totale du circuit quand toutes les résistances sont de 10 Ω.
(b) Quel est le courant dans la ligne principale si VT est de 100 V?
2. Calculez, dans le cas de la figure 5-2, la puissance totale fournie par la source aux quatre lampes de 100 W.
3. En vous reportant au schéma de la figure 5-15:
Figure 5-15 Pour le problème 3.
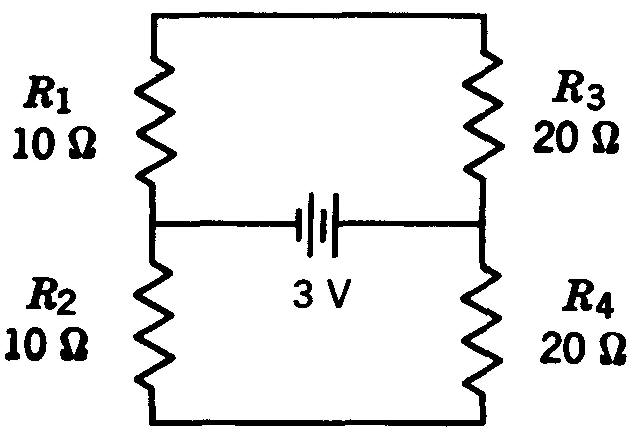
(a) pourquoi la résistance R1 est-elle en série avec R3 mais pas avec R2?
(b) Trouvez la résistance totale du circuit aux bornes de la pile.
4. Deux résistances R1 et R2 de 60 Ω en parallèle doivent être soumises à une tension de 60 V pour qu'un courant de 1 A circule dans chaque branche.
Montrez comment il faut brancher une résistance en série dans la ligne principale pour abaisser la tension de 100 V appliquée à 60 V aux bornes du jeu de résistances en parallèle,
(a) Quelle doit être la tension aux bornes de R3?
(b) Quel est le courant qui doit traverser R3?
(c) Quelle doit être la valeur de la résistance R3?
(d) Si R3 est coupé, quelle est la tension aux bornes de R1 et de R2?
(e) Si R1 est coupé, quelles seront les tensions aux bornes de R2 et de R3?
5. En vous reportant au schéma de la figure 5-16,
Figure 5-16 Pour le problème 5
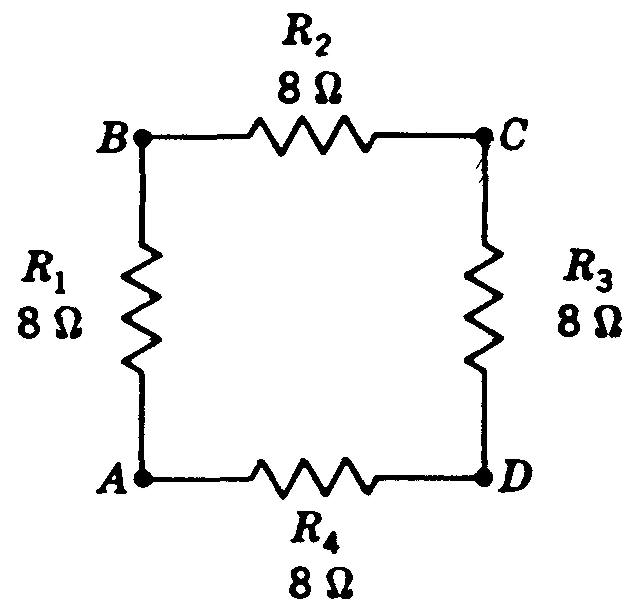
(a) calculez la résistance R entre les points A et D.
(b) Quelle est la valeur de la résistance R entre les points A et D quand la résistance R4 est coupée?
6. Montrez comment connecter quatre résistances de 100 Ω dans un circuit mixte ayant une résistance équivalente de 100 Ω.
(a) Si l'ensemble est branché aux bornes d'une source de 100 V, quelle est la puissance fournie par la source?
(b) Quelle est la puissance dissipée dans chaque résistance?
7. Les quatre résistances suivantes sont en série avec une source de 32 V: R1 = 24 Ω, R2 = 8 Ω, R3 = 72 Ω et K4 = 240 Ω.
(a) Trouvez la chute de tension aux bornes de chaque résistance,
(b) Calculez la puissance dissipée dans chaque résistance,
(c) Quelle est la résistance dans laquelle la chute de tension est la plus élevée?
(d) Quelle est la résistance qui dissipe la puissance la plus élevée?
8. Les quatre mêmes résistances sont branchées en parallèle aux bornes de la source de 32 V.
(a) Trouvez le courant dans chaque résistance,
(b) Calculez la puissance dissipée dans chaque résistance.
(c) Quelle est la résistance parcourue par le courant le plus élevé?
(d) Quelle est la résistance qui dissipe la puissance la plus élevée?
9. Trouvez les résistances R1 et R2 d'un diviseur de tension qui reçoit 10 mA d'une source de 200 V, avec une chute de tension de 50 V dans R2.
10. En vous reportant à la figure 8-2 du chapitre 8, calculez RT, IT, chacune des tensions et chacun des courants.
11. Dans le circuit en pont de Wheatstone de la figure 5-17, trouvez chacune des tensions, indiquez la polarité, et calculez Rx. Le pont est équilibré.
12. Trouvez V et I pour chacune des quatre résistances de la figure 5-18.
13. Calculez RT sur la figure 5-19.
Figure 5-19 Pour le problème 13.
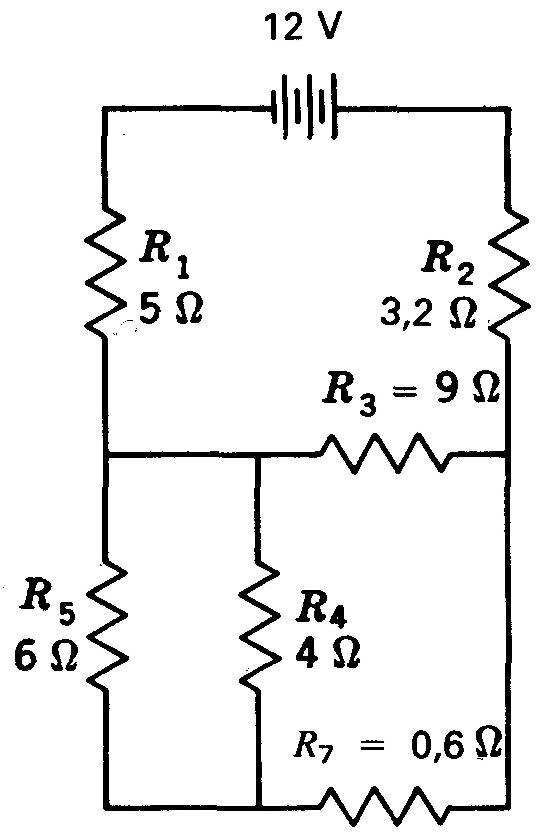
14. Trouvez V6, sur la figure 5-20.
Figure 5-20 Pour le problème 14.
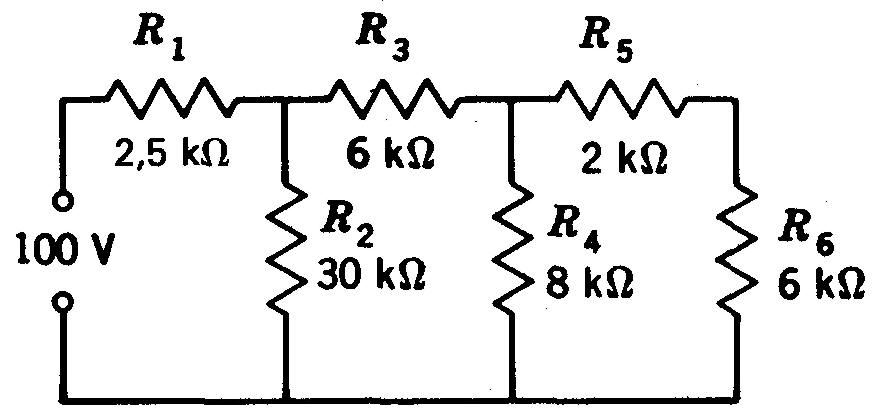
15. D'après la figure 5-21: (a) calculez V2; (b) trouvez V2 quand R3 est coupé.
Figure 5-21 Pour le problème 15.
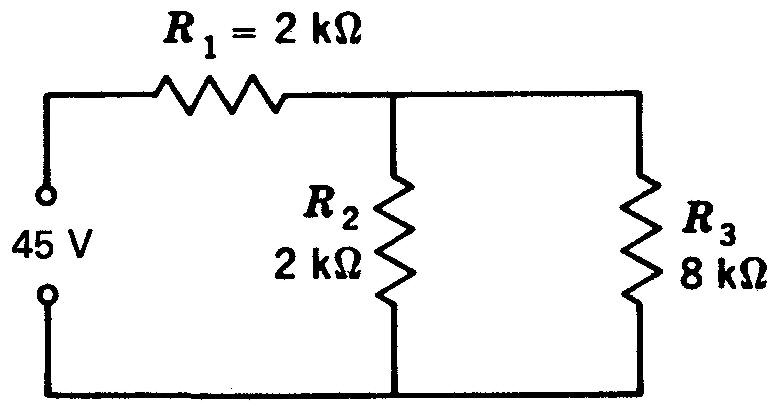
16. D'après la figure 5-22, trouvez I et V pour les cinq résistances et calculer la tension appliquée VT.
Figure 5-22 Pour le problème 16.
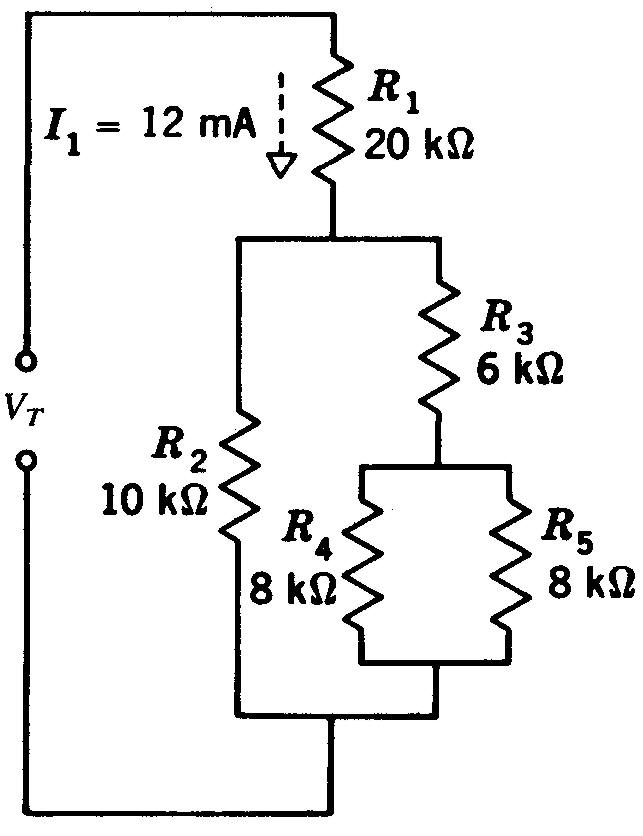
17. D'après la figure 5-23:
Figure 5-23 Pour le problème 17.
(a) trouvez V1; V2, V3, Jl5 J2, /3 et IT dans le circuit représenté,
(b) Reliez maintenant le point G à la masse. Donnez les tensions avec la polarité, aux bornes A, B et C par rapport à la masse. Donnez aussi les valeurs de I1, I2, I3 et IT, quand le point G est à la masse.
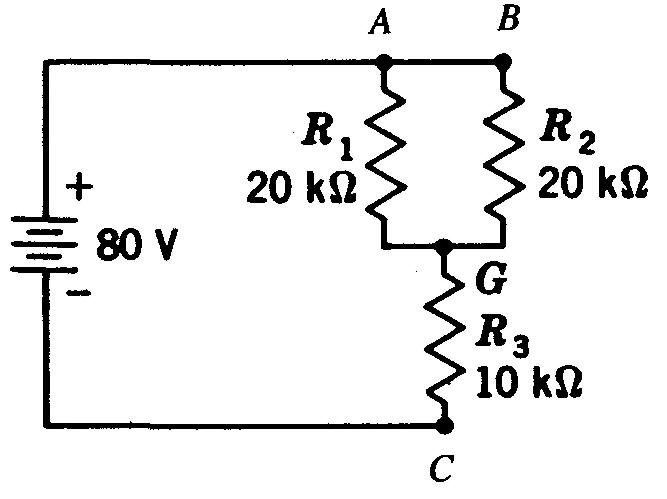
D'après la figure 5-24,
Figure 5-24 Pour le problème 18.
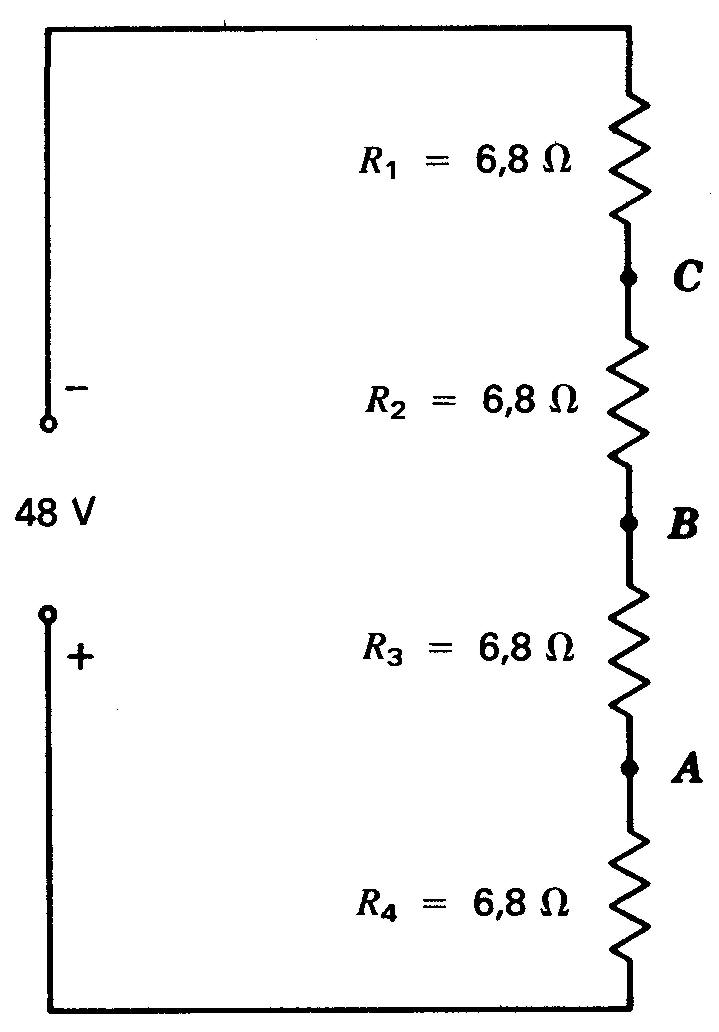
donnez les tensions aux points A, B et C, avec leur polarité par rapport à la masse, quand:
(a) le point A est à la masse; (b) le point B est à la masse; (c) le point C est à la masse.
