
Quelques applications pratiques du palan
Les palans servent à une foule de travaux comportant le déplacement ou l'élévation des fardeaux. Les cinq ou six combinaisons qu'on en peut faire prêtent à une multitude d'opérations aussi bien sur la terre ferme qu'à bord des navires. Les machines lourdes, le chargement des marchandises à bord des navires, les chaloupes de sauvetage et une foule d'autres fardeaux sont déplacés, soulevés ou descendus à l'aide de ces machines.

Les palans d'étai (yard and stay tackles) servent surtout dans les circonstances où, en plus de soulever une charge, il faut la déplacer sur une courte distance. La fig. 23 montre de quelle manière la charge est d'abord soulevée par le palan de vergue pendant que le palan d'étai reste inactif. Une fois que la charge a été hissée au niveau voulu pour éviter toute obstruction, le palan d'étai est mis à contribution pendant que l'autre est relâché, permettant ainsi à la charge de se déplacer latéralement.
Un coup d'œil sur la disposition du câble vous permet de constater que ces deux palans ne confèrent qu'un avantage mécanique de 2. On serait porté à croire que ce n'est guère la peine d'installer deux palans pour l'obtenir que le double de puissance en vue de mouvoir une caisse de 400 livres. Mais les quelques minutes consacrées à cette installation peuvent épargner plusieurs heures d'inactivité à celui qui, à force de bras, risquerait de se donner un tour de rein en déplaçant cette même caisse.
Lorsqu'on veut multiplier les avantages mécaniques, il est toujours avantageux d'avoir recours au double palan volant (luff upon luff). Ce dispositif permet de soulever de très lourdes charges. La fig. 24 fait voir comment les câbles y sont employés.
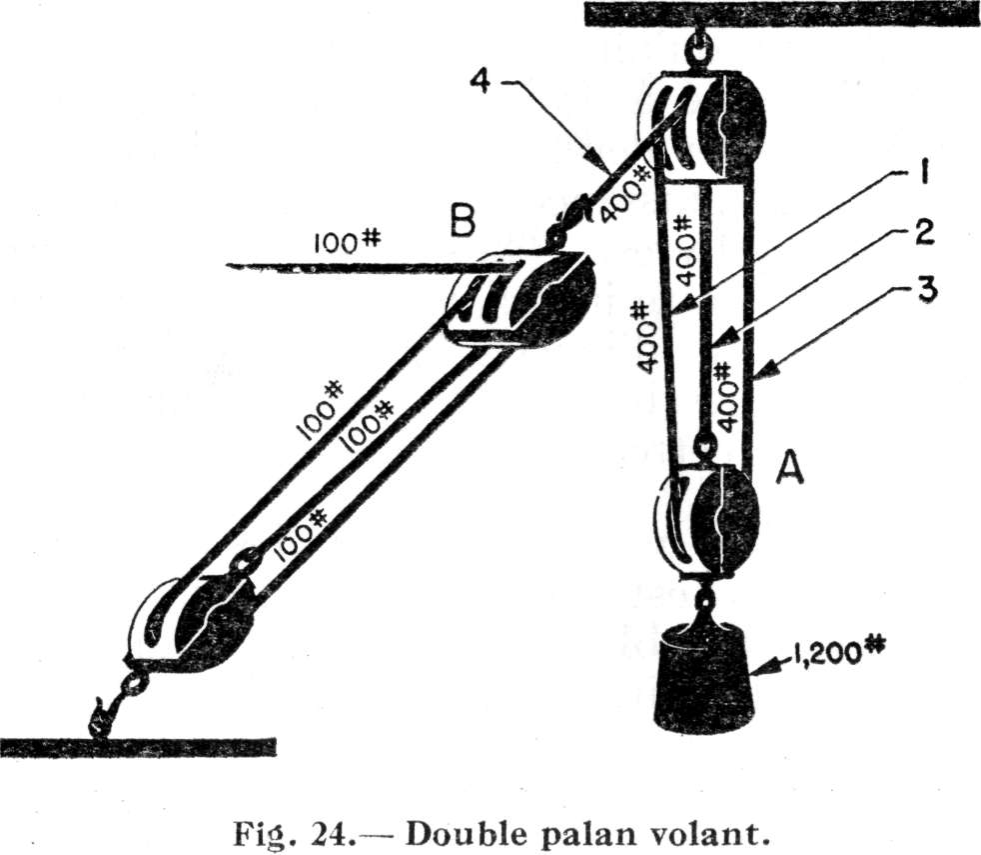
En se basant sur la règle empirique de compter les brins qui aboutissent à la poulie libre pour calculer les avantages mécaniques obtenus par ce type de palan, on se rend compte que la poulie "A" assure un avantage de 3 à 1, tandis que la poulie "B" en assure un de 4 à 1. L'avantage mécanique obtenu du palan "A" se trouve multiplié par 4 par le palan "B", de sorte que le gain total d'un double palan volant est le produit de l'avantage de chacune des deux poulies, soit 12. Il ne faut pas se contenter d'additionner les avantages mécaniques de chaque poulie, il faut les multiplier l'un par l'autre.
Il est facile de calculer les A.M. de l'installation que fait voir la fig. 24. Supposons que la charge à soulever pèse 1,200 livres. Puisqu'elle est supportée par les brins 1, 2 et 3 qui passent par la poulie mobile "A", il s'ensuit que chacun des brins supporte le tiers de la charge, soit 400 livres chacun. Et si le brin 3 subit une traction de 400 livres, le brin 4, qui est fixé à la poulie mobile "B" du deuxième palan, subit également une traction de 400 livres. Quatre brins aboutissent à la poulie mobile "B" du deuxième palan et chacun de ces brins doit supporter une part égale de la traction de 400 livres, soit 100 livres. Par conséquent, il suffira d'exercer une traction de seulement 100 livres sur le brin de garant du palan "B" pour soulever la charge totale de 1,200 livres suspendue au palan "A", ce qui représente un avantage mécanique de 12.
Dans nombre d'ateliers on rencontre des palans dits à chaîne (chain hoist) ou palans de Weston (differential pulley). D'ordinaire, ces palans sont suspendus à un rail aérien (overhead trolley), et l'on s'en sert pour soulever les objets lourds, ainsi que pour les transporter d'un endroit de l'atelier à l'autre.
Afin qu'il soit plus facile de comprendre le fonctionnement d'un palan de Weston, il importe de bien examiner notre fig. 25.

Si vous tirez sur la chaîne "E" jusqu'à ce que la poulie "A" ait fait un tour complet, il est clair que votre effort aura permis à la chaîne de parcourir toute la circonférence de cette poulie, soit 2πR. Dans ce cas, de combien la poulie inférieure et la charge qu'elle supporte auront-elles été soulevées ?
Voici comment on résout le problème:
Du fait que la poulie "C" est une simple poulie mobile, son centre sera élevé de seulement la moitié de la distance qu'a parcourue la chaîne "E", soit l'équivalent de πR. Toutefois, la poulie "B", plus petite que la poulie "A"mais rigidement assujettie à cette dernière, accomplit un tour complet en même temps que "A", de sorte que "B" va donner un peu plus de chaîne à "C". La longueur de la chaîne ainsi cédée sera égale à la circonférence de "B", ou de 2πR. En outre, puisque "C" est une poulie simple mobile, le mouvement descendant de son centre sera égal à seulement la moitié de la longueur de la chaîne qui lui sera cédée, soit πr.
Naturellement, "C" ne tourne pas d'une distance de πR en montant, pour redescendre ensuite d'une distance πr. En fait, son mouvement vers le haut est soutenu et correspond à la différence entre les deux (πR— πr). Le diamètre de la poulie mobile "C" importe peu: il n'affecte en rien les calculs. D'habitude, il est un peu plus grand que "B" et un peu plus petit que "A".
L'avantage mécanique obtenu par le palan à chaîne correspond donc à la distance que parcourt la chaîne "E" divisée par la distance que parcourt le fardeau soulevé. On appelle cela une relation de vitesse, ou un avantage mécanique théorique. Cet avantage est purement théorique, en effet, car la résistance résultant de la friction en réduit la valeur. Il ne faut pas oublier que tous les organes mobiles perdent une partie de l'effort qu'ils doivent transmettre par suite de la résistance provenant de la friction.
Pour trouver le pourcentage d'un avantage mécanique théorique, on peut avoir recours à l'équation suivante

et dans le cas actuel

Si "A" est une roue d'un grand diamètre et "B" d'un diamètre légèrement plus petit, la valeur de 2R devient importante et celle de (R-r) devient moindre. On obtient alors un chiffre important pour

qui est l'avantage mécanique théorique.
Il est possible de soulever de fortes charges à l'aide d'un palan à chaîne. A seule fin de donner une idée de l'avantage mécanique qu'il assure, supposons que la roue la plus grande a un rayon R de 6 pouces et la plus petite un rayon r de 5¾ pouces. Pour trouver l'avantage mécanique théorique, on utilise la formule
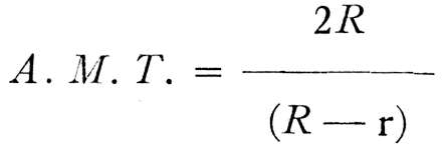
et en substituant des chiffres aux lettres, on obtient la solution suivante:
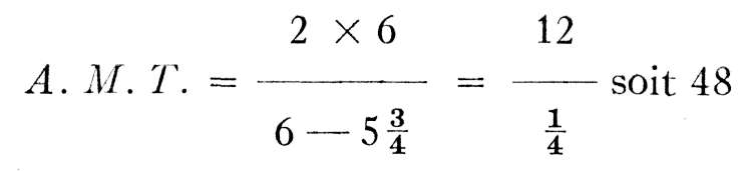
Du fait .qu'une friction considérable s'exerce dans ce type de machines, l'avantage mécanique réel n'est assurément pas aussi élevé que le fait voir l'équation théorique. Ainsi, dans le cas que nous venons d'exposer, il faudrait conclure qu'avec une traction de 1 livre on peut soulever 48 livres. Dans la pratique, toutefois, une traction de 1 livre ne devrait guère soulever plus qu'une vingtaine de livres, le reste de l'effort appliqué se perdant à neutraliser la friction.
