Puissance des machines hydrauliques

Dans l'utilisation des machines hydrauliques, il importe de connaître quelle relation existe entre la force appliquée et le résultat obtenu.

La fig. 89 va nous permettre de bien saisir cette relation. Le tube replié en forme de U que l'on y aperçoit, a un diamètre interne correspondant à un pouce carré. Dans chacun des bras du tube se trouve un piston du même diamètre, mais qui peut librement se mouvoir verticalement en flottant au-dessus du liquide que contient le coude. Si vous placez un poids d'une livre sur l'un des pistons, l'autre s'élèvera immédiatement au sommet du bras où il se trouve. Mais si vous placez un poids d'une livre sur chacun des pistons ils resteront tous deux à leur niveau original, comme permet de le constater le croquis de la fig. 90

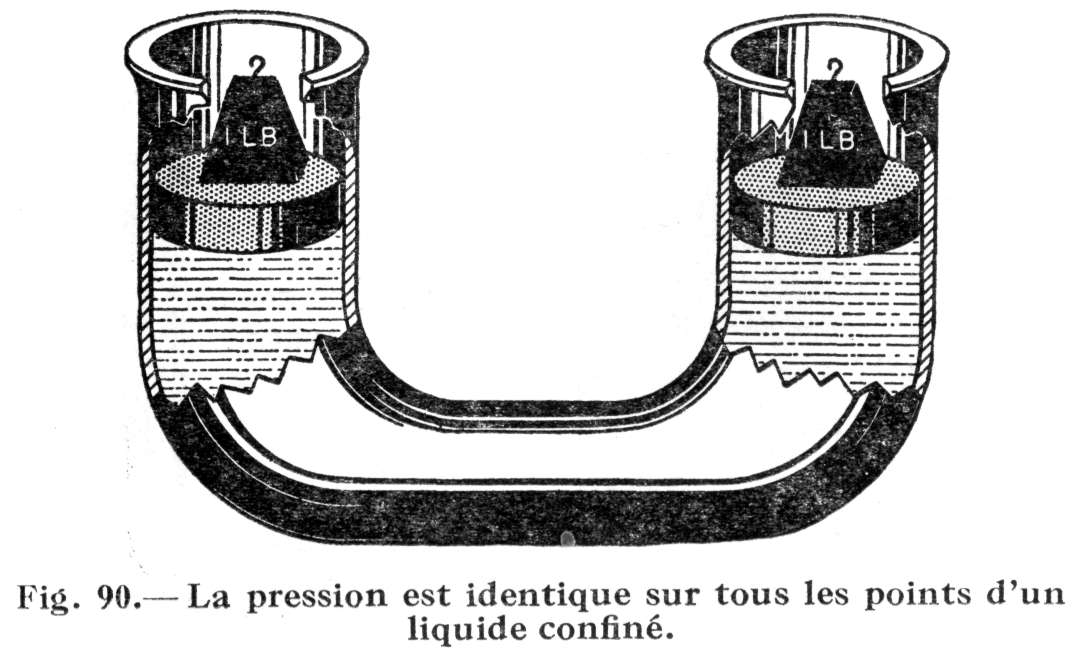
On en conclut qu'une pression d'une livre par pouce carré qui s'exerce de haut en bas sur le piston de droite produit une pression d'une livre par pouce carré, mais cette fois de bas en haut, dans le piston de gauche. En d'autres termes, non seulement la force est-elle transmise par le liquide à travers la courbe en U du tube, mais encore cette force est la même à chaque point d'un pouce carré de la surface interne du contenant. La longueur du tube importe peu; le nombre des courbes qu'il décrit n'a aucune importance non plus.

Ce qui compte principalement, c'est que le contenant soit rempli de liquide; une machine hydraulique ne peut fonctionner normalement s'il y a de l'air de logé dans les canalisations ou les cylindres du système.

Jetons maintenant un coup d'œil sur la fig. 91. Le piston de droite a une surface d'un pouce carré, tandis que celui de gauche en a une de 10 pouces carrés. Si vous placez un poids d'une livre sur le piston du petit cylindre, le liquide transmettra une pression équivalente à ce poids contre chaque pouce carré de la surface interne de tout le système. Du fait que le piston de gauche a une surface de 10 pouces carrés, et que chacun de ces pouces carrés reçoit une poussée d'une livre, il s'ensuit que le piston de grand diamètre reçoit une poussée totale de 10 livres. Si l'on pose un poids de 10 livres sur ce piston il sera équilibré par la force d'une livre appliquée au petit piston.

Par conséquent, dans le cas qui nous occupe, une poussée d'une livre se transforme en une force de 10 livres. L'avantage mécanique obtenu est de 10. C'est la preuve que les machines hydrauliques peuvent jouer un rôle important. Voici une formule qui permet de calculer quelles sont les forces à l'œuvre dans une machine de ce genre:

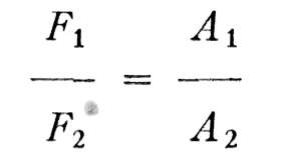
dans laquelle:

Fi = la force, en livres, qui est appliquée au petit piston ;

F2 = la force, en livres, qui est appliquée au grand piston;

A1 = la surface du petit piston, en pouces carrés;

A2 = la surface du grand piston, en pouces carrés.

Mettons cette formule à l'essai afin de trouver le rendement de la presse hydraulique dont notre fig. 92 fait voir schématiquement le mécanisme.

Le grand piston a une surface de 90 pouces carrés et le petit une surface de seulement 2 pouces carrés. Le bras de la pompe exerce une force de 15 livres sur le petit piston. Essayons de trouver avec quelle force totale le grand piston sera poussé de bas en haut.

Appliquons la formule :

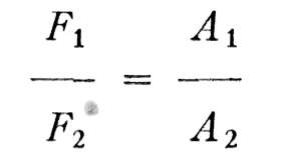
Par substitution, on obtient:

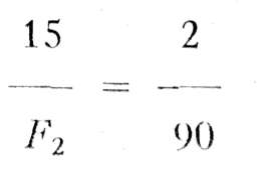
et nous obtenons:

Recherche personnalisée