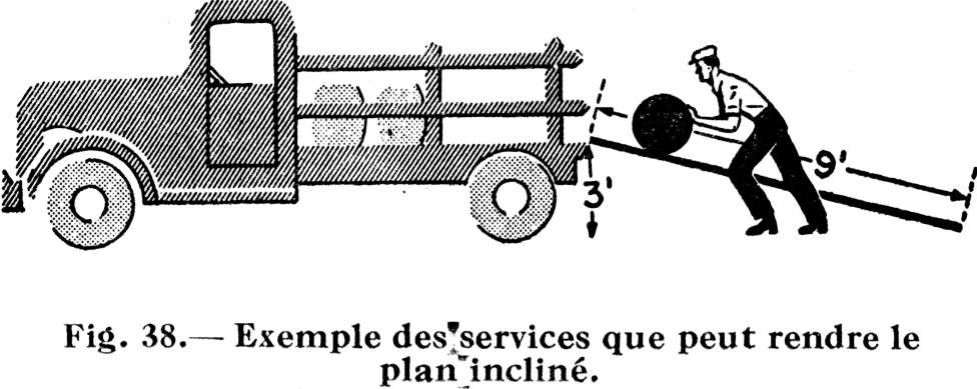
Le plan incliné

Vous avez sans doute eu l'occasion de voir à l'œuvre les livreurs de bière lorsqu'ils chargent des barils sur leur camion. Le camion est reculé jusqu'à la chaîne de trottoir. Le livreur installe une plate-forme ou une échelle à deux montants en pente du trottoir sur l'arrière de son camion de manière à former une rampe, puis il roule les barils «amont» cette rampe.

Un baril de 32 gallons peut peser dans les alentours de 300 livres s'il est rempli, et ce serait toute une tâche d'en faire le chargement

à force de bras. C'est pourquoi les livreurs se munissent d'une de ces machines élémentaires qu'on appelle un plan incliné (inclined plane). Les plans inclinés servent à une multitude d'autres fins. Une passerelle de navire, une route de montagne construite en pente douce, une rampe à bestiaux, en sont des exemples courants.

Le plan incliné permet de vaincre une résistance relativement forte en appliquant un effort beaucoup moindre sur une distance plus grande que la hauteur dont on veut élever une charge.

On se rend compte, en examinant la fig. 38, que le livreur, pour élever un baril de 3 pieds au-dessus du trottoir et le charger dans son camion, se sert d'une rampe de 9 pieds. S'il ne disposait pas de cette rampe, il serait obligé d'appliquer un effort de 300 livres afin d'élever verticalement le baril de 3 pieds. Grâce à la rampe, cependant, il peut exercer son effort sur toute la longueur des 9 pieds à mesure que le baril se rapproche de la plate-forme du camion. Dans ces conditions, il est tout naturel qu'il ne dépense que les 3/9 de l'effort qu'il devrait appliquer directement. Les 3/9 de 300 donnent 100 livres et c'est précisément l'effort qu'il déploie.

En fait, si nous revenons à la formule dont il a été question au Chapitre I, on a:

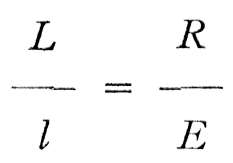
dans laquelle

L = la longueur de la rampe,

l = la hauteur au-dessus du sol,

R = le poids de l'objet à soulever ou abaisser,

E = l'effort requis pour soulever ou abaisser l'objet.

En appliquant cette formule au cas actuel, on trouve:

L = 9 pieds; l = 3 pieds; et R = 300 livres

Si l'on substitue ces chiffres aux lettres de la formule, on obtient:

Du fait que la rampe est trois fois plus longue que haute, elle assure un avantage mécanique de trois. Pour trouver l'avantage mécanique théorique, il suffit de diviser la distance totale sur laquelle s'exercera l'effort appliqué, par la distance verticale que devra parcourir l'objet qu'on veut élever ou abaisser.