La roue mandrinée ou manivelle

Avez-vous déjà essayé d'ouvrir une porte dont la poignée est absente ? Si jamais cette expérience vous a été imposée, vous savez jusqu'à quel point il est difficile de faire tourner avec les doigts le petit axe carré qui actionne le pêne à ressort de la porte. Cette expérience assez fâcheuse vous a sans doute permis de mieux apprécier l'avantage que procure le bouton ou poignée (door knob) dans le fonctionnement normal d'une serrure. La poignée de porte est un exemple courant des services que rend cette autre machine simple qu'on appelle la roue mandrinée ou emmanchée sur un axe.

Le volant d'une automobile, la manivelle d'une baratte à beurre, le vilebrequin, voilà autant d'applications familières de ce genre de machine élémentaire. Comme vous avez pu vous en rendre compte par l'emploi de ces divers appareils, la roue emmanchée sur son axe contribue à amplifier de beaucoup l'effort appliqué. Lorsqu'il est impossible de poser une vis à l'aide d'un tournevis ordinaire parce que le bois est trop dur, il suffit de placer ce même instrument dans le mandrin d'un vilebrequin pour obtenir un avantage mécanique marqué et vaincre la résistance du bois à la pénétration de la vis.

Un principe doit être établi dès le début. La machine formée d'une roue emmanchée sur son axe est constituée d'une roue ou d'une manivelle rigidement assujettie à ce même axe de façon à rendre les deux absolument solidaires pour ne former qu'un tout. Il découle de ce principe que les roues avant d'une automobile, par exemple, ne sauraient être assimilées à ce genre de machines du fait que leur axe ne tourne pas solidairement avec elles.

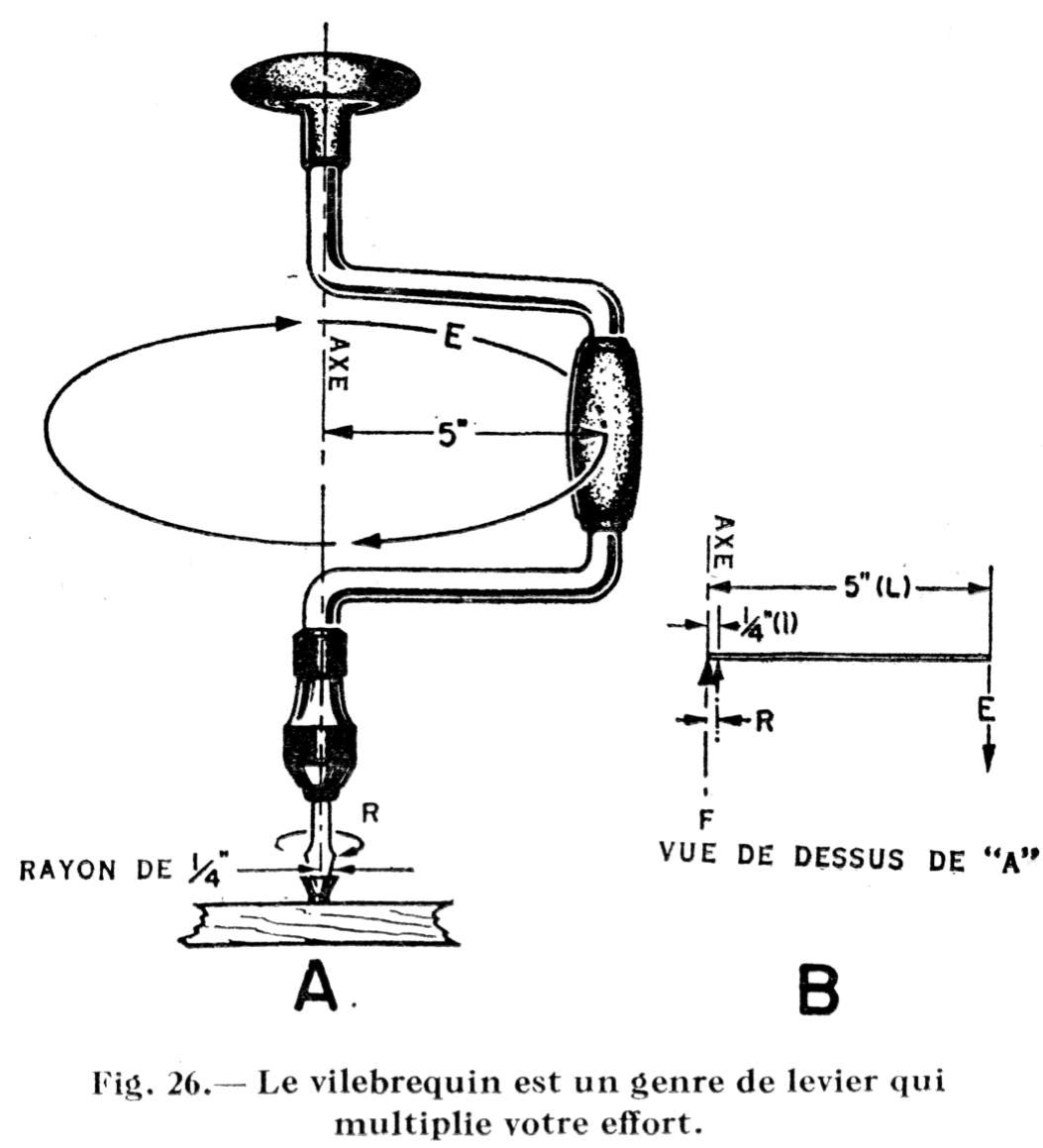
Comment le dispositif de la roue mandrinée accroît-il l'effort appliqué ? Commençons par examiner la fig. 26A.

On y voit un vilebrequin dans le mandrin duquel est emmanchée une pointe de tournevis. L'effort de l'ouvrier portera sur la manivelle, qui décrira un mouvement circulaire dont le rayon est de 5 pouces. Si Ton suppose qu'un effort de 10 livres soit appliqué sur cette manivelle, essayons de trouver quelle force s'exercera contre la résistance offerte par la vis, en admettant que le rayon de la lame du tournevis est de ¼ de pouce.

Le vilebrequin peut être considéré dans le présent cas comme un levier du deuxième genre. (Voir fig. 26B).

On trouvera le degré de résistance à vaincre en ayant recours à la formule suivante

dans laquelle

L = le rayon du cercle que décrit la manivelle, l = la moitié de la largeur de la lame du tournevis, R = la force de résistance offerte par la vis, E = l'effort appliqué contre la manivelle par l'ouvrier.

Si l'on substitue les chiffres réels aux lettres de la formule, on obtient:

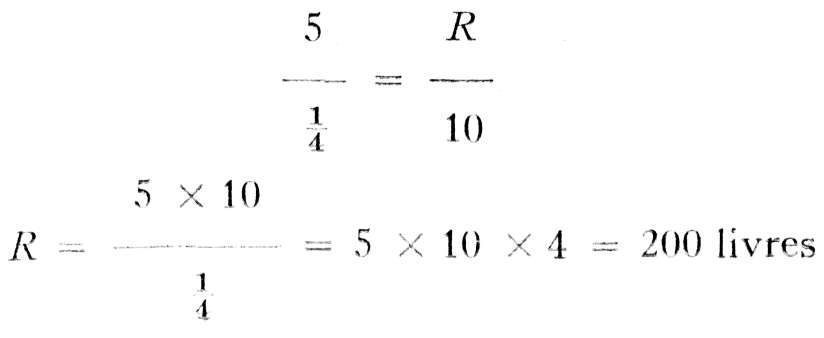
En d'autres termes, la lame du tournevis exercera sur la tête de la vis une force de torsion correspondant à 200 livres. La relation qui existe entre les rayons ou diamètres, ou entre les circonférences d'une roue mandrinée avec ceux du mandrin ou axe qui forme avec elle un tout, donne une idée de l'avantage mécanique résultant de ce type de machine élémentaire.

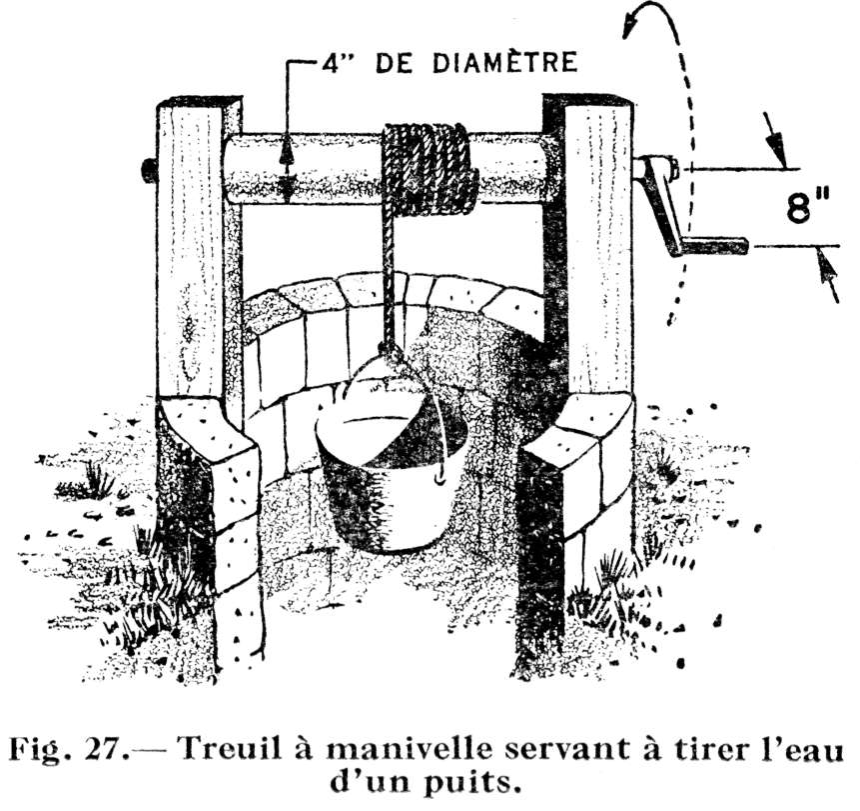
Prenons un autre cas. Autrefois, on tirait l'eau des puits au moyen d'un seau qu'un treuil permettait de descendre et de remonter avec relativement peu d'efforts. En admettant, comme le fait voir notre fig. 27, que la distance du centre de l'axe à la poignée de la manivelle du treuil soit de 4 pouces, et que le tambour autour duquel s'enroule le câble ait un rayon de 2 pouces, on obtient un avantage mécanique de 4. Cet important avantage explique l'emploi généralisé des appareils de ce genre.

Accélération

Dans une multitude d'applications, on se sert du principe de la roue mandrinée dans le but d'accélérer le mouvement. La roue dentée sur laquelle s'enroule la chaîne d'une bicyclette, agissant solidairement avec la roue arrière, constitue l'un de ces applications. En pédalant, le cycliste applique un effort contre la roue dentée d'un diamètre plus petit que la roue motrice à laquelle elle est assujettie. En admettant que la roue dentée ait 8 pouces de circonférence et la roue motrice 80 pouces, il est clair qu'à chaque tour accompli en une seconde, la roue dentée avancera de 8 pouces. Mais comme la roue motrice lui est solidaire, un point quelconque du pneu se déplacera pendant la même durée de 80 pouces sur la route. Il s'ensuit qu'à la même vitesse de rotation des deux roues on obtient un gain ou accélération de 10 dans la vitesse circonférentielle, du fait de leur différence de diamètre.

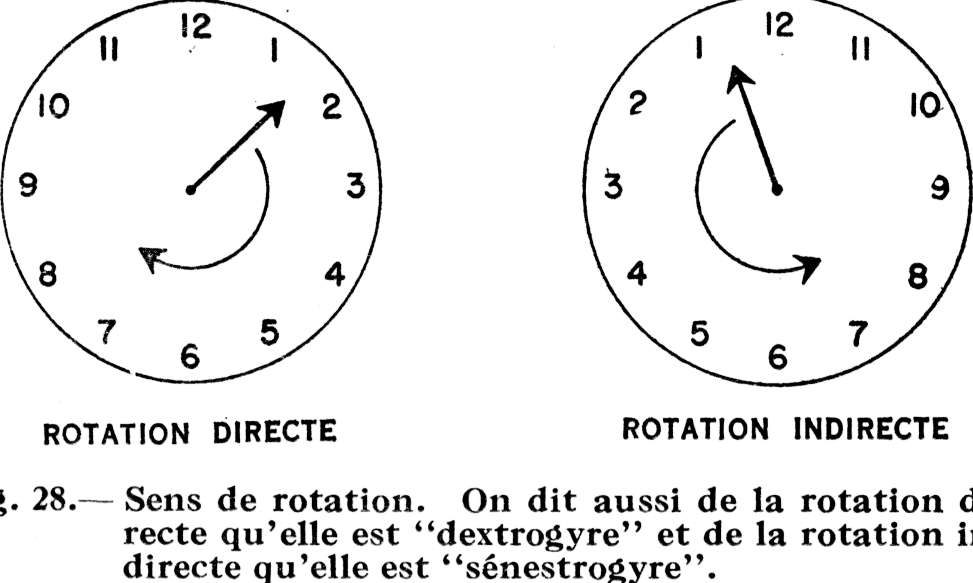
Voici une suggestion qui vous permettra sans doute de mieux saisir les avantages mécaniques obtenus grâce à la roue mandrinée aussi bien qu'avec d'autres genres de machines. Vous avez probablement observé que l'effort appliqué contre un levier tend à le faire tourner autour de son point d'appui. Vous avez également vu qu'en tirant sur le câble d'un palan on provoque la rotation de sa poulie, et qu'en tournant le volant d'une auto on provoque la rotation de la colonne de direction. Toutes les fois qu'on applique un effort contre un levier ou la jante d'une roue, on provoque une rotation autour du point d'appui ou de l'axe dans un sens ou dans l'autre. Si cette rotation s'accomplit dans le même sens que les aiguilles d'une montre, on dit qu'elle est positive (clockwise), si elle s'accomplit dans le sens opposé, on dit qu'elle est négative (counterlockwise). Un coup d'œil sur la fig. 28 fait immédiatement comprendre ce qu'on entend par ces termes.

Nous avons vu que le résultat d'un effort agissant sur la poignée d'un vilebrequin dépend non seulement de la puissance de cet effort, mais aussi de la distance qui sépare la poignée du centre de rotation. Dorénavant, ce résultat sera désigné sous l'appellation de moment de torsion ou couple (torque).

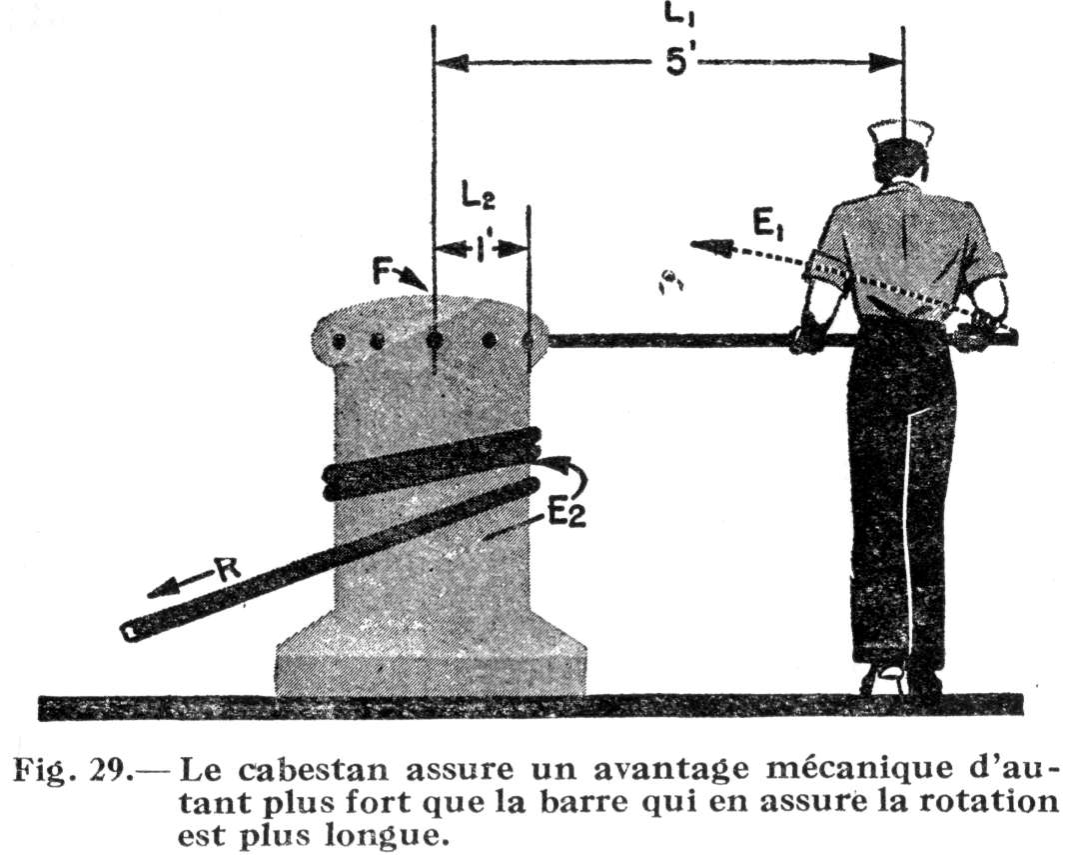
Réfléchissez un instant sur l'effet du mouvement contraire aux aiguilles d'une montre qu'accomplit la barre du cabestan dans notre fig. 29. Ici, le moment de torsion est désigné par E₁ et la distance qui sépare le point où cet effort est appliqué du centre de l'axe par L₁ Par conséquent, E₁ x L₁ est le moment de torsion. Il convient de noter que cette expression comprend à la fois la somme d'effort et la distance qui sépare le point où l'effort est appliqué du centre de l'axe.

D'ordinaire, la distance est mesurée en pieds et la force appliquée en livres. Par conséquent, les moments de torsion (moment of force) s'expriment en pieds/livres. Au lieu d'écrire moment de torsion, on se contente le plus souvent, de désigner ce phénomène par moment.

En se servant d'une barre plus longue, le matelot de notre fig. 29 peut augmenter l'efficacité de son effort sans dépenser une seule once d'énergie supplémentaire. Par contre, s'il applique toujours le même effort, mais à un point plus rapproché du tambour de son cabestan, le moment de torsion sera moindre.

Équilibre des forces

S'il arrivait que le câble "R" qui s'enroule autour de son cabestan vienne à se rompre, le matelot de notre fig. 29 s'étendrait de tout son long sur le pont du navire. Mais du moment que le câble résiste, le matelot peut continuer à pousser sur la barre du cabestan. Il travaille à rencontre d'un moment positif de torsion qui est égal en magnitude, mais en sens opposé, à son propre moment négatif de torsion. Le moment de résistance, tout comme le moment d'effort, dépendent de deux facteurs. Dans le cas du moment de résistance, ces facteurs sont:

1° la force R₂ avec laquelle le fardeau tire sur le câble et,

2° la distance L₂ qui sépare le centre du cabestan de la périphérie du tambour.

L'existence de cette force de résistance se révélerait immédiatement si le matelot laissait la barre du cabestan à elle-même. Le poids du fardeau suspendu au bout du câble forcerait celui-ci à se dévider d'autour du cabestan en imprimant au tambour de ce dernier un rapide mouvement positif. Le principe en jeu ici c'est que des moments positifs et négatifs étant équilibrés, la machine reste inactive ou avance à une vitesse constante.

Cet équilibre des forces peut se résumer par l'expression:

UN MOMENT POSITIF = UN MOMENT NÉGATIF

et puisqu'un moment de torsion est le produit de la somme du nombre de fois que le moment s'éloigne du centre de rotation, cette expression d'équilibre peut se résoudre dans la formule

dans laquelle:

E₁ = le moment de l'effort

L₁ = la distance du point d'appui ou de l'axe au point où s'applique l'effort

E₂ = le moment de résistance

L₂ = la distance du point d'appui ou centre de l'axe au point où la résistance se fait sentir

Premier exemple :

Appliquons cette formule à un problème se rapportant au cabestan. Une barre de cabestan ayant 5 pieds de longueur est fichée dans le tambour d'un cabestan ayant un rayon de 1 pied. On veut soulever un fardeau de ½ tonne avec ce cabestan. Quel sera l'effort que devra déployer le marin pour actionner la barre du cabestan ?

Nous venons de voir que

Ici, L₁ = 5; E₂ = 1,000 livres; et L₂ = 1.

Substituons ces valeurs aux lettres de la formule et nous trouvons:

donc

Deuxième exemple:

Examinons à présent le cas pénible dont la fig. 30 nous relate discrètement l'histoire.

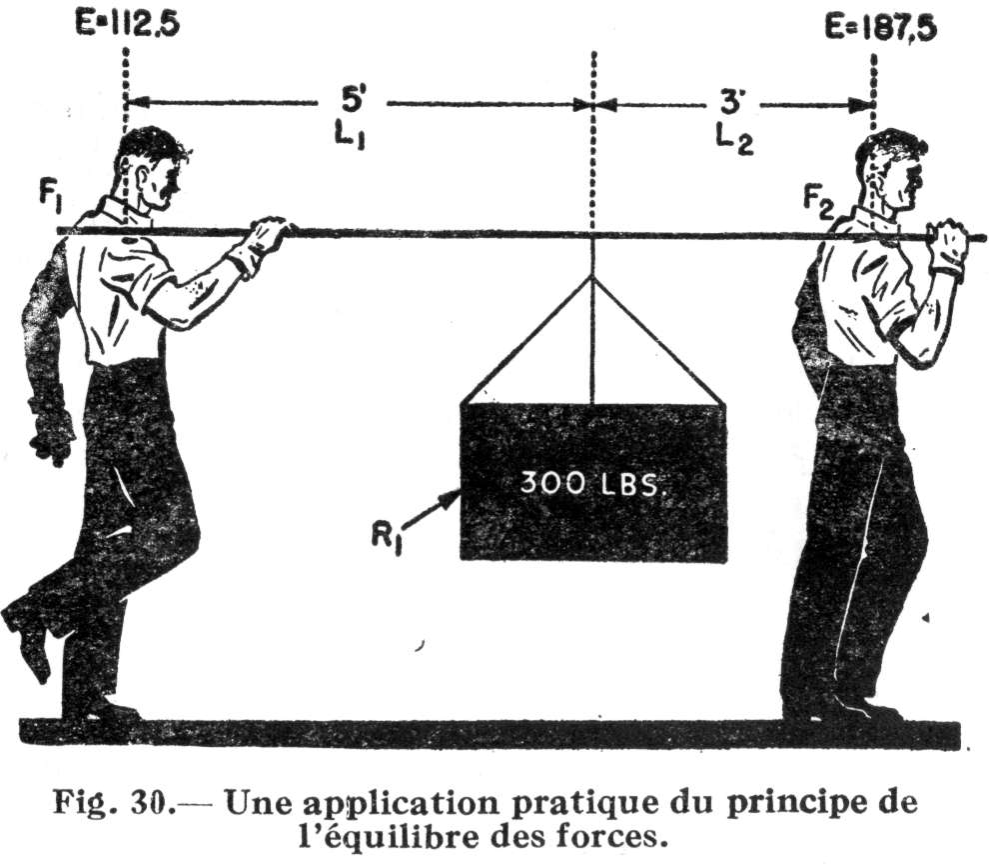
Ayant à transporter une caisse de 300 livres, Pitre a suggéré à Jacques qu'on la suspende à une barre de fer longue de 10 pieds. Mais au moment de soulever la charge, Pitre, d'un geste adroit mais peu charitable, fit glisser la barre vers lui de façon à ce que la charge ne se trouve plus qu'à 3 pieds de Jacques. Il sait fort bien que Jacques, ainsi «attelé», portera une partie passablement plus forte que lui-même de la charge.

Et voici l'explication de ce truc. Considérons l'épaule de Pitre comme un point d'appui F₁ puis le moment positif (dans le sens des aiguilles d'une montre) que provoque la charge de 300 livres. Cette charge est à 5 pieds de l'épaule de Pitre. Si R₁ est la charge, et L₁ la distance séparant l'épaule de Pitre de la charge, le moment positif M_a est

L'épaule de Pitre agissant encore comme point d'appui, la résistance créée par l'effort de Jacques provoque un moment négatif (dans le sens opposé au mouvement des aiguilles d'une montre) et qui agit contre le moment de la charge. Ce moment négatif M_b est égal à l'effort de Jacques multiplié par E₂ fois la distance L₃ de son épaule au point d'appui F₁ constitué par l'épaule de Pitre. Du fait que L₂ = 8 pieds, la formule devient:

Mais aucune rotation ne se produit, de sorte que le moment positif et le moment négatif sont équivalents. M_a = M_b. Par conséquent:

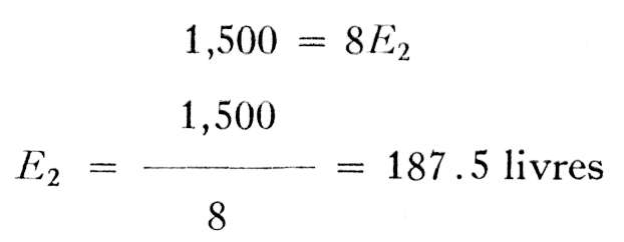
Ainsi donc, ce pauvre Jacques supporte 187.5 livres de la charge de 300 livres.

Mais quel est donc le poids que supporte Pitre ? Naturellement, la différence entre 187.5 et 300, soit 112.5 livres. Mais vous pouvez vérifier en ayant recours au calcul suivant:

Cette fois, c'est l'épaule de Jacques qu'il va falloir prendre comme point d'appui F₂. Le moment négatif M_c est égal à la charge de 300 livres multipliée par Ri fois la distance L₂ soit 3 pieds, qui la sépare de l'épaule de Jacques, ce qui donne: Mc = 300 X 3 - 900 pieds/livres. Le moment positif M_d est le résultat de l'effort de Pitre, E₁, qui agit à une distance L₃ du point d'appui. L₃ = 8 pieds. Donc, puisque le moment négatif égale le moment positif, on a

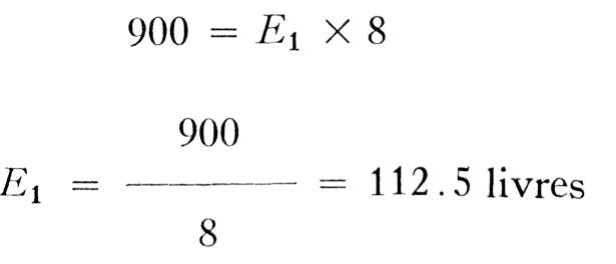
Pitre, qui sans doute souffre d'un tour de rein et n'a pas voulu taxer ses forces au-delà de leurs limites, ne se trouve à porter que 112.5 livres par le simple fait qu'il a su tirer avantage de ses connaissances en mécanique appliquée.

Le couple

Examinez bien la fig. 31.

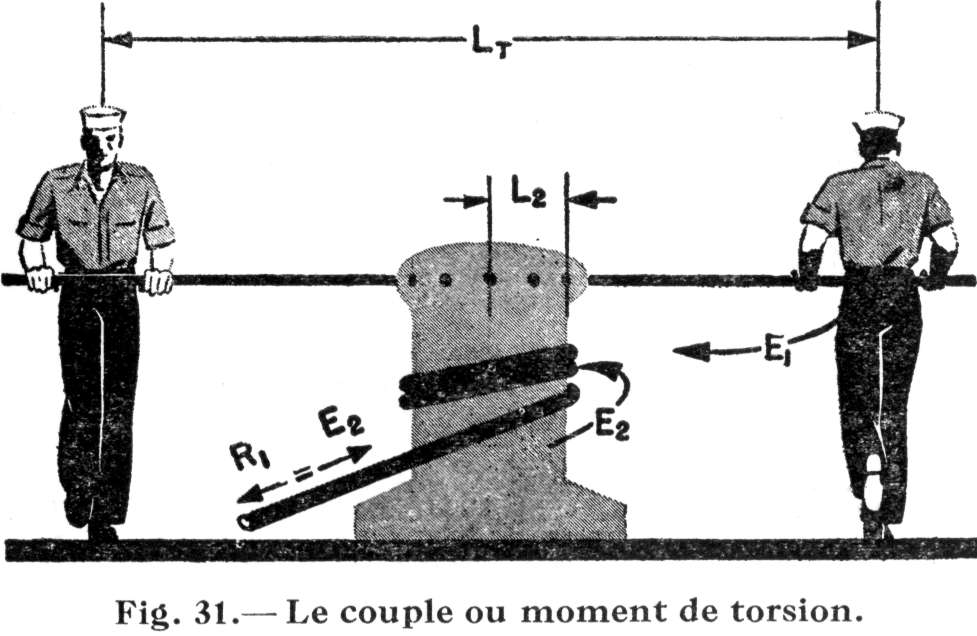
On y voit un autre problème concret que présente l'utilisation du cabestan. Afin d'accroître l'effort appliqué, on a inséré une deuxième barre dans le tambour du cabestan, à l'opposé de celle qui s'y trouvait tout à l'heure, et un autre marin a été installé. Selon toute apparence, si l'on se base sur la place que chacun occupe, ces deux marins poussent dans des directions opposées. Mais du fait qu'ils sont placés de chaque côté de l'axe tournant constitué par le cabestan, leur effort produit effectivement une rotation en sens unique. Et si les deux marins exercent leur poussée respective avec une force égale, le moment de torsion qu'ils produisent sera deux fois plus fort que si un seul d'entre eux accomplissait ce travail. En termes techniques, nous avons là un couple.

On s'en rend compte, le couple est une application particulière de la roue mandrinée sur un axe. Le moment de torsion qui résulte du couple est égal au produit de la distance totale L_t entre les deux points où l'effort est appliqué et la force Et appliquée par UN marin. Cette équation s'écrit comme suit:

Pour résumer

Voici, en résumé, les principaux points qu'il importe de retenir au sujet du principe de la roue mandrinée sur un axe

•—Une machine élémentaire de ce genre doit être constituée d'une roue solidement assujettie à un axe. La roue et l'axe doivent tourner solidairement.

•—La roue mandrinée à son axe peut servir soit à augmenter votre effort, soit à l'accélérer.

•—L'effet d'un effort qui tend à faire tourner un objet autour d'un axe ou point d'appui est appelé moment de torsion ou couple, ou simplement moment.

•—Lorsqu'un objet est stationnaire ou se déplace à un rythme soutenu, les moments positifs sont égaux et opposés aux moments négatifs.

•—Les moments de torsion dépendent de deux facteurs; l'effort appliqué et la distance qui sépare le point d'appui, ou axe, du point où l'effort est appliqué.

•—Lorsque deux efforts d'égale force sont appliqués à égale distance de chaque côté de l'axe et se déplacent en sens contraire de manière à provoquer une rotation autour de l'axe, on obtient un couple.

Recherche personnalisée