Efficacité

Efficacité, rendement

Jusqu'ici, il n'a guère été question de l'effet que produit la friction sur les machines. En ne tenant pas compte de la friction, le fonctionnement théorique des machines s'explique avec plus de facilité, mais tout le monde sait par expérience que la friction entre en jeu chaque fois que deux surfaces glissent l'une contre l'autre. Naturellement, l'effort servant à vaincre la résistance engendrée par la friction reste perdu en tant qu'est concerné le travail utile. Puisqu'il en est ainsi, il devient évident que l'on doit faire entrer dans une machine une somme plus grande de force qu'il n'en sortira en travail utile. Autrement dit, une machine n'est jamais efficace à 100 pour cent.

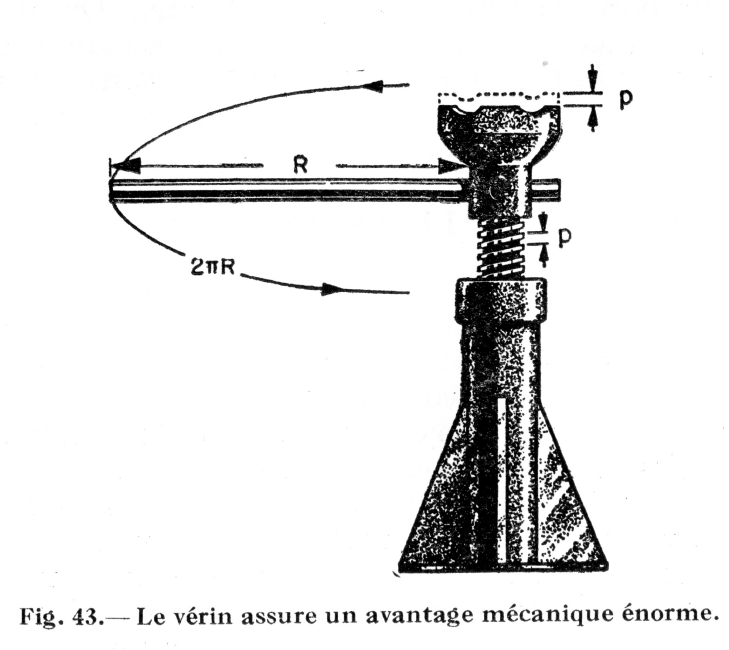
Prenez le vérin de la fig. 43, par exemple. Il est fort possible qu'en appliquant un effort de seulement 2 livres sur son levier on ne parviendra pas à soulever le fardeau du tout et qu'il faudra plutôt exercer sur ce même levier un effort de 10 livres. Dans ce cas, il faudrait conclure que seulement 2 livres sur 10, soit 20 pour cent de l'effort appliqué, servent effectivement à accomplir un travail utile. Les autres 8 livres d'effort sont dépensées à vaincre la résistance de friction engendrée par la machine. Sous les circonstances, le vérin n'aurait que 20 pour cent d'efficacité. En fait, la plupart des vérins sont des machines à très faible rendement utile, mais en dépit de leur faible efficacité, on exerce grâce à eux une poussée énorme en n'y appliquant qu'un effort modéré.

Un moyen très simple de calculer quelle est l'efficacité d'une machine quelconque consiste à diviser ce qu'on y met par ce qui en sort:

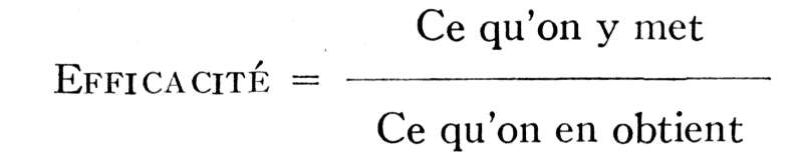
Si l'on veut bien, à présent, se reporter au problème du palan illustré par la fig. 66,

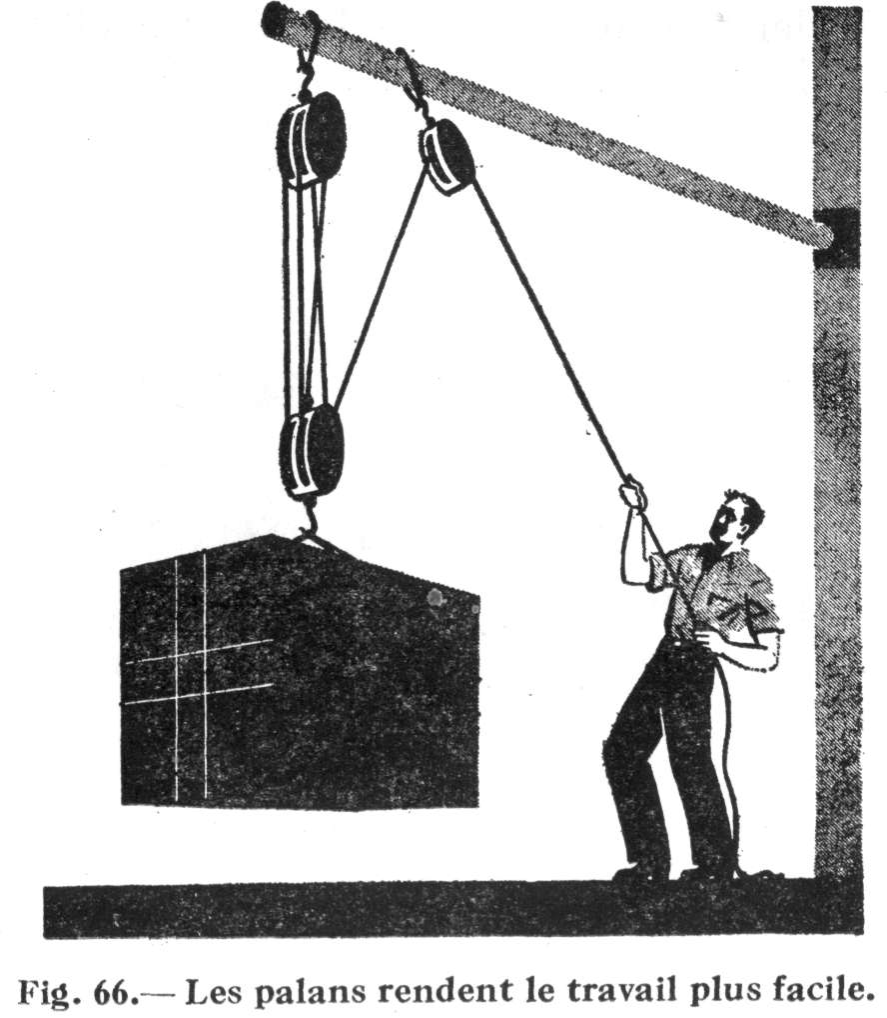
on verra qu'au lieu d'exercer une traction de seulement 120 livres, le manœuvre devra tout probablement mettre 160 livres de traction en halant 100 pieds de câble pour soulever sa caisse de 600 livres à 20 pieds de hauteur. Pour se rendre compte de l'efficacité du palan employé à cette fin, on peut recourir à la formule suivante:

En substituant les chiffres réels aux lettres de la formule, on obtient:

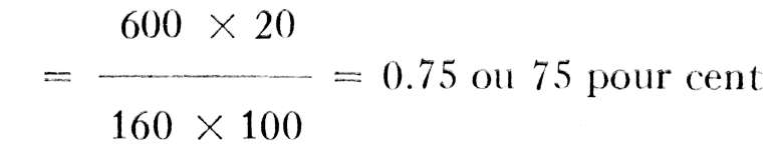
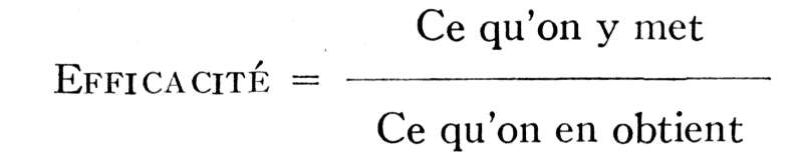
Théoriquement, avec l'avantage mécanique de 12 qu'assure le treuil de la fig. 57, on devrait être en mesure de soulever une charge de 600 livres en n'exerçant qu'un effort de 50 livres sur la manivelle. Mais si cette machine ne possède que 60 pour cent d'efficacité, quel effort faudra-t-il exercer réellement pour obtenir le résultat désiré ? Pour le trouver, il suffit de prendre 60 pour cent de 50 livres, soit 50 / 0.60 = 83.3 livres. On peut cependant vérifier en ayant recours à la formule:

Une révolution du tambour élèvera la charge de 600 livres d'une hauteur de S2 de 2 π r ou de 7.85 pieds. Pour faire accomplir UN tour au tambour, le petit engrenage doit faire SIX tours, et comme la manivelle qui lui est fixée a un rayon plus grand, elle parcourt une distance de S1 de 6 X 2 π R, ou de 94.2 pieds. Alors, par substitution, on obtient:

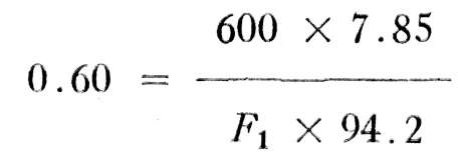
et:

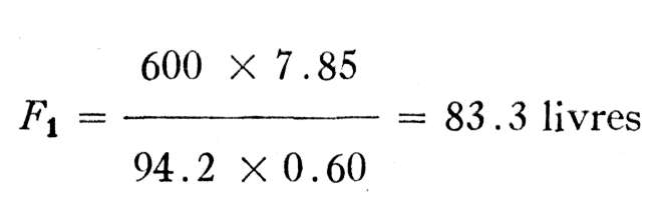
Parce que cette machine ne possède que 60 pour cent d'efficacité, il va falloir y mettre un effort de 94.2 X 83.3 ou de 7,847 pieds/livres de manière à en obtenir un rendement utile de 4,710 pieds/livres. La différence entre le rendement mécanique théorique et le rendement mécanique réel, 7,857 - 4,710 = 3,137 pieds/livres, se perd à vaincre la friction qui se produit entre les divers organes de la machine.

Recherche personnalisée