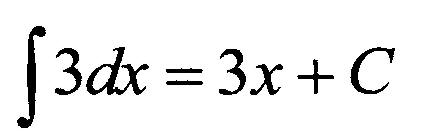
Champs de pente

La pente d'une équation linéaire quantifie sa variation de y pour chaque augmentation unitaire de x.

Par exemple, considérons cette fonction linéaire :

f(x) = 3x + 1

La pente de cette fonction est de trois : pour trois unités, le graphique se déplace vers le haut (montée), il se déplace d'une unité vers la droite (course).

La dérivée d'une fonction révèle sa pente. Ainsi, la dérivée de f(x) = 3x +1 est

confirmant que la pente de la fonction est de trois. Mais concentrons-nous maintenant sur cette équation :

f'(x) = dy/dx =3

Appelée équation différentielle, toute fonction ayant une pente de trois satisfait l’équation.

Ainsi, en plus de f(x) = 3x +1, nous pourrions avoir f(x) = 3x - 1, ou f(x) = 3x + 6, ou f(x) =3x + C, où C est un terme constant.

Et en effet, la primitive de trois est donnée par:

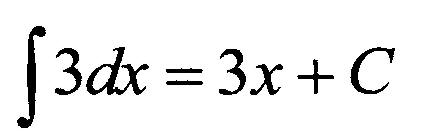
Ainsi, toute fonction linéaire sous la forme f(x) = 3x + C satisfait l'équation différentielle indiquée ci-dessus.

Nous pourrions représenter graphiquement la fonction différentielle dy/dx = 3 sur le plan de coordonnées ; ces types de graphiques sont appelés champs de pente, qui montrent la pente de la fonction à des coordonnées sélectionnées dans tout le plan.

Un champ de pente de dy/dx = 3 montrerait des segments de ligne courts, tous inclinés avec une pente égale à trois, dispersés dans tout le plan.

Supposons plutôt que notre équation différentielle ait été

dy/dx =3x

Nous recherchons maintenant une fonction qui a une pente de 3x pour n'importe quel ensemble de coordonnées donné.

Par exemple, la pente de la fonction au point (2,4) serait 3 * (2) = 6 , et la pente de la fonction au point (-5,2) serait égale
3 * (- 5) = -15.

Grâce à l'intégration, on peut trouver la fonction (ou plus précisément, la famille de fonctions) qui satisfait à ce critère :

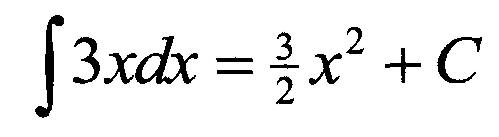
Cette famille de fonctions est parabolique. Un champ de pente de dy/dx = 3x montrerait des segments de ligne courts de pente variable répartis de manière parabolique à travers le plan de coordonnées.

Notez que les champs de pente peuvent être constitués de toutes les équations différentielles, mais que toutes les équations différentielles ne peuvent pas être intégrées.

Le programme DIFF.BAS, qui dessine les champs de pente à l'écran, vous offre des options lors de la saisie de votre équation différentielle, bien que, comme vous n'avez pas besoin de saisir l'équation directement dans le code, il existe des limitations.

 Cependant, vous pouvez saisir deux équations à la fois.

Lors de l'exécution, il vous sera demandé de saisir vos équations sous la forme suivante : (C1*Y1^P1) + (C2*Y2^P2), où C1 et C2 sont les coefficients et PI et P2 sont les puissances des deux variables.

Une fois que tous les coefficients et puissances des deux équations ont été saisis, DIFF.BAS mappe le champ de pente. En appuyant sur la touche ESCAPE, vous terminez le programme.

Notez que, comme XYGRAPH.BAS (Graphiques d'équations), le code doit convertir un écran graphique en plan de coordonnées, qui possède à la fois des coordonnées négatives et positives. les lignes 74 et 75 traitent les calculs quelque peu complexes.

Même si c'est un bon début, DIFF.BAS a besoin de plus d'options de visualisation afin de le rendre vraiment utile.

Les échelles de x et y, ainsi que la fenêtre de visualisation, ne doivent pas simplement être définies sur des valeurs fixes. Et les familles d’équations différentielles que le programme peut représenter graphiquement sont également extrêmement limitées.

DIFF.BAS

10 KEY OFF:SCREEN 9:COLOR 15,0:CLS
20 PRINT"DEUX ÉQUATIONS DIFF SERONT SOUS LA FORME SUIVANTE:"
21 REM ---(C1*Y1^P1) + (C2*Y2^P2) POUR Y1 ET Y2
30 PRINT"Sous la forme:(C1*Yl^P1) + (C2*Y2^P2) POUR Y1 ET Y2"
40 INPUT "C1";C1:INPUT"P1";P1:INPUT"C2";C2:INPUT"P2";P2
45 INPUT "C3";C3:INPUT"P3";P3:INPUT"C4";C4:INPUT"P4";P4
50 REM--LA PARTIE AFFICHAGE
55 CLS
56 PSET(0,175),4:DRAW"R650":PSET(320,0),4: DRAW"D350"
57 LOCATE 1,46:PRINT "Y1=";C1;"Y1^";P1;" + ";C2;"Y2^";P2
58 LOCATE 2,46:PRINT"Y2=";C3;"Y1^";P3;" + ";C4;"Y2^";P4
65 FOR R=1 TO 349 STEP 20:Y1L=T:Y2L=R
70 FOR T=1 TO 639 STEP 20:Y1L=T:Y2L=R
71 FOR U=1 TO 10
74 Y2=(C3*-((T-320)/(10+(-T-320)/10*P3))^P3)+(C4*-((R-175)/(10+(-R-175)/10*P4))^P4)+R
75 Y1=(C1*-((T-320)/(10+(-T-320)/10*P1))^P1)+(C2*-((R-175)/(10+(-R-175)/10*P2))^P2)+T
76 LINE(Y1L,Y2L)-(Y1,Y2),14:Y1L=Y1:Y2L=Y2
78 NEXT U
90 NEXT T,R
100 I$=INKEY$
110 IF I$<>CHR$(27) THEN 100
120 CLS