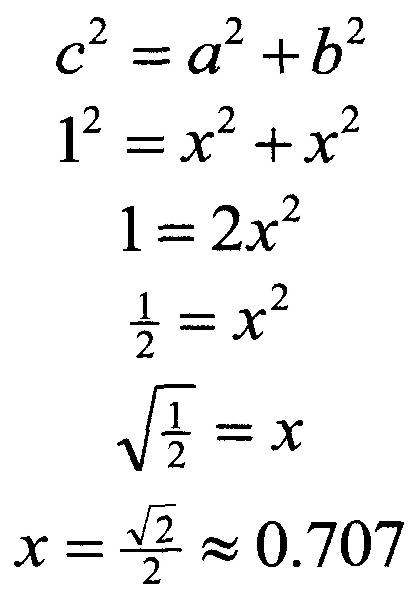
Rotation avec la trigonométrie

La rotation des graphiques autour de l'écran est un peu plus délicate que le simple déplacement d'images, inchangées, à gauche ou à droite ou vers le haut ou vers le bas.

Dans la section suivante, nous examinerons une manière simple, intégrée à GW-BASIC, de faire pivoter des images, mais dans cette section, nous approfondirons un peu les mathématiques de la rotation.

Imaginez un cercle unité, c'est-à-dire un cercle d'un rayon d'une unité (les unités peuvent être n'importe quoi : pouces, mètres, miles, années-lumière, cela ne fait aucune différence).

Imaginez également que le centre de ce cercle unité soit situé à l'origine du plan de coordonnées.

Chaque paire de coordonnées sur le cercle peut non seulement être représenté par un (x,y) ; chaque paire de coordonnées peut également être donnée sous la forme (cosθ,sinθ), où la lettre grecque θ (prononcée « theta ») représente l'angle de rotation en radians (vous vous souviendrez peut-être que 2π équivaut à 360 degrés, ou une rotation complète dans le sens inverse des aiguilles d'une montre sur le plan de coordonnées).

Pour comprendre pourquoi, il faut un peu de trigonométrie.

Supposons qu’à partir de la base de l’axe des x positif, nous traçons une ligne formant un angle de 45 degrés qui traverse le cercle unité.

Considérons le segment de ligne qui part de l'origine au point d'intersection (x, y) sur le cercle unité à l'hypoténuse d'un triangle rectangle.

À partir de (x, y), tracez une ligne vers le bas et perpendiculairement à l'axe des x positif.

 Cela nous donnera un triangle rectangle situé dans le cercle unité. Plus précisément, un triangle rectangle spécial : un 45-45-90, ce qui signifie que les angles intérieurs sont de 45, 45 et 90 degrés.

On connaît déjà la longueur de l'hypoténuse de ce triangle particulier : c'est une unité, puisque l'hypoténuse sert aussi de rayon au cercle unité.

Dans cet esprit, utilisons le théorème de Pythagore pour trouver les deux autres côtés (qui, bien sûr, ont la même longueur, puisqu'ils sont des angles opposés avec la même mesure) :

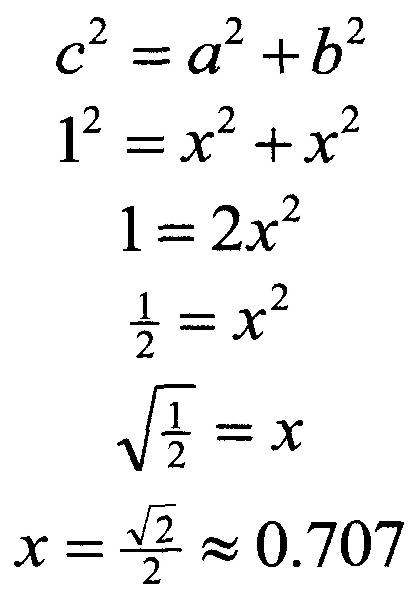
Puisque les deux côtés (non hypoténuse) du triangle rectangle spécial ont des longueurs d'environ 0,707, nous pouvons dire que
le point (x,y) qui, rappelons-le, est le point du cercle unité que traverse la ligne tracée à un angle de 45 degrés – est en réalité à:

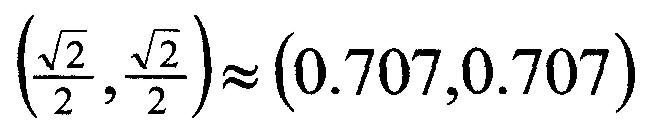
De même, nous pourrions trouver les coordonnées d’angles de n’importe quel multiple de 45 degrés.

Et comme il existe également un triangle spécial 30-60-90, les angles multiples de 30 degrés sont également faciles à trouver.

Ces détails, ainsi que la trigonométrie derrière la recherche des coordonnées d'angles plus compliqués, sont laissés au lecteur intrépide.

Mais, même si nous venons de trouver les coordonnées d'un seul point, cela ne relie toujours pas les deux rapports trigonométriques sinus et cosinus au point (x, y), ce que nous essayions initialement de faire.

Vous vous souvenez des définitions du sinus et du cosinus de l’école ?

Sinon, les voici :

sinθ = côté opposé / hypoténuse

cosθ = côté adjacent / hypoténuse

Les termes « opposé » et « adjacent » font référence respectivement au côté opposé et au côté adjacent (c'est-à-dire à côté) de l'angle d'intérêt sur un triangle rectangle.

Cependant, avec le cercle unité, l'hypoténuse est un rayon et a donc la valeur un. On peut donc réexprimer les deux rapports comme:

sinθ = côté opposé / 1 = côté opposé

cosθ = côté adjacent / 1 = côté adjacent

En reconsidérant les coordonnées d'angle de 45 degrés ci-dessus, qui ont été calculées à partir d'un triangle à l'intérieur du cercle unité, cela signifie que :

Avec un peu plus d'expérimentation (en trouvant les coordonnées des angles en dehors du premier quadrant), on se rend compte qu'en tout point (x, y) du cercle unité :

(x, y) = (cos θ, sin θ)

qui relie parfaitement toutes les paires de coordonnées aux rapports trigonométriques.

Bien que le mode graphique de SCREEN 7 ne soit pas configuré comme un axe de coordonnées (par exemple, lorsque vous descendez sur l'écran de votre ordinateur, les valeurs y augmentent plutôt que diminuent) nous pouvons nous appuyer sur la trigonométrie pour faire pivoter un point autour d'un cercle au centre de l'écran, laissant dans son sillage des traînées multicolores de pixels.

Après une courte pause, l'écran s'efface et vous verrez une ligne blanche tourner autour de l'écran.

 Exécutez UNITCIR.BAS et SINCOS.BAS pour voir les spectacles circulaires et colorés.

Une matrice de rotation peut également permettre des rotations de coordonnées sur un plan (ou dans l'espace) par rapport à un angle θ.

Considérons cette matrice de rotation :

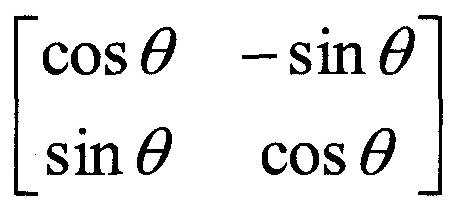
Par exemple, si nous souhaitons faire pivoter le point (5,5) d’un angle de 45 degrés par rapport à l’origine, l’opération de multiplication matricielle suivante aboutit aux nouvelles coordonnées.

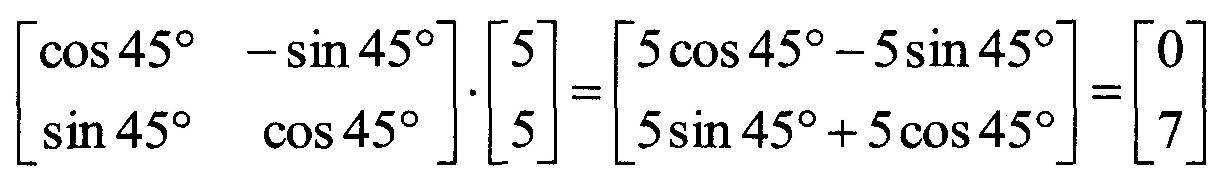
Ainsi, les coordonnées (5,5) pivotées d'un angle de 45 degrés par rapport à l'origine aboutissent à (0,7).

En général, alors, on peut dire que toute rotation sous un angle θ autour de l'origine est donnée par:

Le programme ROTATION.BAS démontre l'utilité de la matrice de rotation.

Notez que UNITCIR.BAS et SINCOS.BAS utilise les fonctions SIN et COS, qui prennent en entrée les radians (plutôt que les degrés).

Notez également que, dans les deux programmes, le STEP est petit ; augmentez un peu le facteur et le cercle ne sera pas continu.

Le programme ROTATION.BAS, bien que similaire à ses frères, utilise la matrice de rotation et l'instruction LINE pour tracer des motifs colorés.

Bien que la rotation d’une ligne soit facile, la rotation d’une forme plus complexe peut s’avérer fastidieuse en utilisant une méthode purement trigonométrique.

UNITCIR.BAS

5 PI=3.14159
10 KEY OFF:SCREEN 7:COLOR 15,0:CLS
20 FOR T=0 TO 2*PI STEP .01
30 PSET(150+COS(T)*30,100+SIN(T)*30),INT(1+15*RND(1))
40 NEXT T
50 FOR PAUSE=1 TO 10000:NEXT PAUSE
60 CLS
70 FOR T=0 TO 2*PI STEP .01
80 LINE (156,100)-(150+COS(T)*30,100+SIN(T)*30),15
85 FOR PAUSE= 1TO 100:NEXT PAUSE
86 CLS
90 NEXT T
100 FOR PAUSE=1 TO 10000:NEXT PAUSE
110 CLS:END

SINCOS.BAS

5 screen 9: COLOR 15,0: key off
10 CLS
20 PRINT"Appuyez <ESC> POUR VOIR LE PROCHAINE DÉMO DE CERCLE"
30 CIRCLE(COS(R)*45+340,SIN(R)*35+140),20,INT(1+15*RND(1))
40 R=R-3.14159/50
45 FOR PAUSE=1 TO 100:NEXT PAUSE
46 IF INKEY$=CHR$(27) THEN 60
50 GOTO 30
60 CLS
62 FOR STEPPER=.1 TO .001 STEP -.01
65 FOR SPIRAL=1 TO 400 STEP STEPPER
70 PSET(COS(R)*SPIRAL+340,SIN(R)*SPIRAL+140),INT(1+15*RND(1))
80 R=R-3.14159/50
90 FOR PAUSE=1 TO 100: NEXT PAUSE
100 NEXT SPIRAL
110 NEXT STEPPER

ROTATION.BAS

10 KEY OFF:SCREEN 9:COLOR 15,0:CLS
20 X=300:Y=200
30 PSET(X,Y),15
35 FOR ANGLE=1 TO 2.32*3.14159 STEP .001
40 X1=(COS(ANGLE)*(X)+(-SIN(ANGLE)*(Y)))
50 Y1=((-SIN(ANGLE))*(X)+(COS(ANGLE)*(Y)))
60 LINE(X,Y)-(X1+200,Y1+200),INT(1+2*RND(1))
70 NEXT ANGLE