Bootstrap

Bootstrap

GW-Basic, utilisé par PC-Basic

Si nous souhaitons estimer un paramètre de population, tel que la taille moyenne des individus dans une population (qu'il s'agisse de personnes, de chiens ou de voitures), un intervalle de confiance est généralement utilisé.

À l'aide d'un petit ensemble de données recueillies (de préférence de manière aléatoire) auprès de la population d'intérêt, un intervalle de confiance d'un seul ensemble de données quantitatives (comme les hauteurs), estimant les limites supérieure et inférieure de la valeur du paramètre, est calculé comme suit :

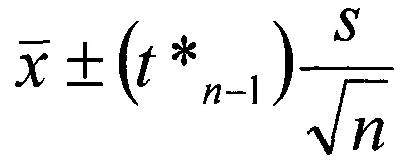
Le X est la moyenne (la moyenne arithmétique) obtenue à partir de l'échantillon de données ;

s représente l'écart type (une mesure de la dispersion moyenne des points de données par rapport à la moyenne) ;

n représente la taille de l'échantillon (le nombre de points de données dans l'échantillon) ;

et t est le score t, qui est extrait de la distribution t, une distribution symétrique en forme de monticule avec une forme variable, en fonction de la taille de l'échantillon ainsi que du niveau de confiance souhaité ;

un niveau de confiance de 95 % est généralement la norme, mais des niveaux de confiance de 90 % (résultant en un score t plus petit) ou de 99 % (un score t plus élevé) sont également courants.

Par exemple, si nous souhaitons estimer le temps moyen que tous les adultes américains passent à regarder la télévision, il est impossible d'échantillonner tous les adultes américains. Un échantillon est donc prélevé dans la population d'intérêt.

Supposons que sur 31 personnes interrogées au hasard, le temps de télévision moyen s'est avéré être de 275 minutes avec un écart type de 16 minutes. Après avoir trouvé le score t approprié, l'intervalle de confiance à 95 % est calculé comme suit :

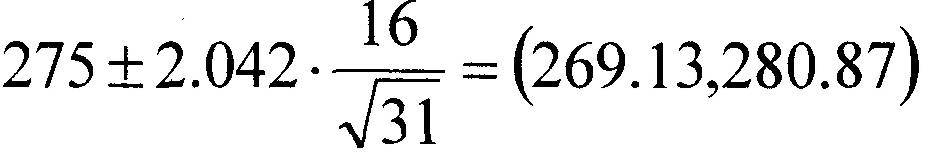
Le problème clé de cette méthode d'estimation réside dans la taille de l'échantillon : bien qu'un résultat statistique important appelé théorème central limite garantisse que l'utilisation de la distribution t avec des tailles d'échantillon supérieures à 30 est mathématiquement valable, des tailles d'échantillon plus petites posent un problème - ce n'est pas toujours évident d'après quel type de répartition de la population ils dérivent.

Ainsi, avec de si petits échantillons, nous pourrions supposer à tort la normalité (c'est-à-dire que la distribution de la population hôte est une courbe en cloche) alors qu'en fait, la variabilité nous a induits en erreur.

Une solution consiste à traiter l'échantillon comme la population d'intérêt et à tirer à plusieurs reprises (avec remplacement, afin que les éléments puissent se répéter) de nombreux échantillons (généralement un millier) de cette « population ».

Ensuite, ces échantillons - appelés réplications ou rééchantillons ou échantillons bootstrap - sont mélangés par ordre croissant, classés par une certaine valeur d'échantillon.

Par exemple, avec l'exemple de télévision ci-dessus, lorsque nous générons chaque rééchantillonnage, le temps de télévision moyen de ce rééchantillonnage particulier est calculé ; lorsque les 1 000 moyennes d'échantillons ont toutes été trouvées, les moyennes d'échantillons sont disposées dans l'ordre du plus bas au plus élevé.

Enfin, pour obtenir un intervalle de confiance de 95 % à partir des données, le 2,5e centile et le 97,5e centile sont trouvés, servant respectivement de bornes inférieure et supérieure de l'intervalle. (Les centiles pour un intervalle de confiance à 90 % seraient le 5e et le 95e ; pour un intervalle de confiance à 99 %, le 0,5e et le 99,5e.)

Bien que le processus de recherche du t-score dépasse la portée de ce texte, si vous êtes intéressé par une explication détaillée de celui-ci et de nombreuses autres techniques statistiques, veuillez vous référer au livre Apophenia's Antidote.

L'avantage de cette méthode de rééchantillonnage, appelée bootstrap, est qu'elle n'est pas paramétrique, c'est-à-dire qu'elle ne suppose aucune distribution de population sous-jacente.

Il y a cependant deux inconvénients:

(1) Le bootstrap gaspille potentiellement des informations, ne produisant pas un intervalle de confiance aussi précis que possible si la distribution de la population pouvait en fait être établie;

et (2) le bootstrap ne peut pas être facilement mis en œuvre à la main : c'est un travail bien adapté à un ordinateur, bootstrapping est relativement nouveau, ayant été découvert il y a seulement quatre décennies par le mathématicien de l'Université de Stanford Bradley Efron.)

Heureusement, vous avez probablement un ordinateur devant vous. Encore plus heureusement, cet ordinateur connaît GW-BASIC, car le programme d'amorçage ci-dessous y est écrit.

Étant donné que la méthode de rééchantillonnage par bootstrap nécessite finalement de trier une liste de données, l'algorithme du tri par sélection - traité en détail dans la section Tri par sélection - est utilisé.

Avec 1 000 échantillons à mettre en ordre croissant, cependant, ne vous attendez pas à ce que votre intervalle de confiance soit calculé rapidement ; selon la vitesse de l'ordinateur, vous devrez peut-être attendre jusqu'à quinze minutes avant de voir le résultat.

Notez également que chaque fois que vous démarrez avec les mêmes données, vos intervalles de confiance ne seront pas nécessairement les mêmes (bien qu'ils soient similaires).

Voici un exemple que vous pourriez envisager d'essayer avec le programme : la participation aux matchs de football à domicile de votre école secondaire locale cette saison, dont il n'y a eu que sept matchs jusqu'à présent, a une répartition inconnue de la population hôte.

Les chiffres de fréquentation sont de 1546, 1790, 908, 893, 1012, 704 et 1310 personnes. À l'aide du bootstrap, calculez les intervalles de confiance à 90 %, 95 % et 99 % pour la fréquentation moyenne de la population. (Le programme BOOT.BAS affichera par défaut les trois intervalles de confiance.)

Les lignes 400 à 470 génèrent les rééchantillons à partir de l'échantillon de données saisies par l'utilisateur. Le problème, encore une fois, est un problème de vitesse : l'algorithme de tri par sélection est mal adapté pour organiser efficacement 1 000 éléments, vous devez donc attendre interminablement vos intervalles de confiance.

Idéalement, l'utilisateur devrait pouvoir demander n'importe quel niveau de confiance, pas seulement 90 %, 95 % et 99 %. L'écriture d'une routine pour capturer les centiles corrects (et, par conséquent, les éléments du tableau) améliorerait considérablement le programme.

De plus, le programme devrait être capable de faire varier le nombre de réplications, et pas simplement de se contenter d'en générer 1 000 à chaque fois.

De plus, il pourrait être avantageux d'ajouter des routines pour amorcer d'autres paramètres de population, tels que la variance, l'écart type et le coefficient de corrélation.

Au fait : pour utiliser le programme pour estimer une proportion de la population, l'ensemble de données d'origine doit être codé avec des zéros pour représenter les échecs et des uns pour représenter les succès ; les moyennes de ces rééchantillonnages binaires dicteront l'intervalle de confiance.

Mais accélérer BOOT.BAS doit être votre priorité absolue. Cela signifie, peut-être, utiliser un tri rapide au lieu d'un tri par sélection.

5 REM BOOT,BAS
10 KEY OFF:CLS
15 DIM ARRAY(1000):DIM DAT(30) 'Déclaration les deux tableaux
16 ELEM=1:I=0
20 PRINT "--- BOOTSTRAPPING POUR TROUVER LA MOYENNE DE LA POPULATION
30 PRINT
32 BOOT=1000 'Génére 1000 rééchantillonnages
40 PRINT "Saisissez vos données, un chiffre à la fois. Entrez un nombre négatif pour terminer."
50 PRINT "Il y a un maximum de 30 points autorisés."
60 WHILE I>=0
70 PRINT "Element #";ELEM;":";
80 INPUT I:DAT(ELEM)=I
90 ELEM=ELEM+1
100 IF ELEM>30 THEN I=-1
120 WEND
130 ELEM=ELEM-2 'Obtient le nombre total d'éléments du tableau
131 TOTAL=ELEM
132 GOSUB 400 'Génère des rééchantillonnages
200 'Mettre en œuvre l'algorithme de tri de sélection
202 FIRST=2 'Définir le "premier" élément
203 ELEM=BOOT
205 WHILE FIRST<=ELEM
210 SMALL=FIRST
220 FOR SEARCH=FIRST TO ELEM
230 'Trouvez le plus petit de ces éléments
240 IF ARRAY(SMALL)>ARRAY(SEARCH) THEN SMALL=SEARCH
250 NEXT SEARCH
260 'Échangez les éléments, si nécessaire
265 IF ARRAY(FIRST-1)>ARRAY(SMALL) THEN GOTO 270 ELSE GOTO 280
270 TEMP=ARRAY(FIRST-1):ARRAY(FIRST-1)=ARRAY(SMALL):ARRAY(SMALL)=TEMP
280 FIRST=FIRST+1 'Incrémenter jusqu'à l'élément "actuel" suivant
290 WEND
300 'Sort l'intervalle de confiance
301 PRINT "Les valeurs des rééchantillons sont "
302 FOR T=1 TO BOOT:PRINT ARRAY(T);" "::NEXT T
303 PRINT
305 PRINT "Un intervalle de confiance à 95 % pour la moyenne est:"
310 PRINT "Borne inférieure:";ARRAY(25) 'Sort le 2,5e centile
320 PRINT "Limite supérieure:";ARRAY(975) "Génére le 97,5e centile
325 PRINT "Un intervalle de confiance à 90 % pour la moyenne est:"
326 PRINT "Borne inférieure:";ARRAY(50) 'Sort le 5e centile
327 PRINT "Limite supérieure:";ARRAY(950) 'Sort le 95e centile
328 PRINT "Un intervalle de confiance à 99 % pour la moyenne est:"
329 PRINT "Borne inférieure:";ARRAY(5) 'Génére le 0,5e centile
330 PRINT "Limite supérieure:";ARRAY(995) 'Génére le 99,5e centile
331 END
400 'Algorithme pour générer les rééchantillonnages
405 RANDOMIZE TIMER
410 FOR A=1 TO BOOT
415 SUM=0
420 FOR B=1 TO TOTAL
430 SUM=SUM+DAT(INT(1+TOTAL*RND(1)))
440 NEXT B
450 ARRAY(A)=SUM/TOTAL
455 PRINT ARRAY(A);" ";
460 NEXT A
465 PRINT "Tri des 1000 rééchantillonnages... Veuillez patienter....."
470 RETURN

Recherche personnalisée