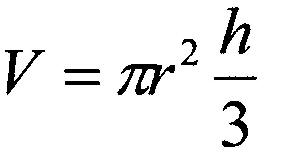
Approximation du cône

GW-Basic, utilisé par PC-Basic

Programme avec Texte Seulement

PC-BASIC

Archimède, un ancien mathématicien grec, a d'abord trouvé l'aire d'un cercle en inscrivant des polygones réguliers d'un nombre croissant de côtés à l'intérieur d'un cercle - essentiellement, il est arrivé au résultat en se rapprochant avec des formes plus simples. Ce processus est courant en mathématiques; par exemple, considérons la règle de Simpson et la règle trapézoïdale, qui se rapprochent de l'intégration numérique.
Supposons que nous souhaitions approximer le volume d'un cône, qui a une base circulaire et converge vers un seul point à son sommet. L'utilisation de cylindres empilés horizontalement finement tranchés - en commençant par la base, et chacun devenant légèrement plus petit - serait probablement la meilleure approche. Le volume d'un cône, soit dit en passant, est donné par

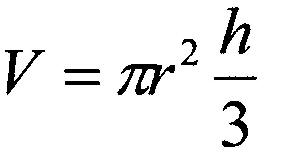
et nous utiliserons cette formule pour voir à quelle distance nos approximations des volumes de cône sont dans CONE.BAS.

Lorsque vous exécutez le programme, on vous demande d'abord à quel point vous souhaitez trancher chaque cône - plus vous tranchez finement, meilleure est l'approximation. Ensuite, après avoir entré le rayon de la base du cône, les résultats apparaissent à l'écran.

Une boucle FOR/NEXT nommée X gère les (peut-être) nombreuses itérations nécessaires pour l'approximation du volume du cône. Des entrées de plus en plus petites pour H, la hauteur du cylindre, prennent sans surprise de plus en plus de temps à traiter par l'ordinateur.

Étant donné que CONE.BAS est construit sur l'estimation du volume d'un cône tridimensionnel, le fait de montrer le cône, ainsi que les cylindres plus simples utilisés pour l'approximer, serait beaucoup plus intéressant visuellement. De plus, d'autres sortes de formes plus complexes - qui n'ont pas de formules toutes faites comme les cônes - pourraient voir leurs volumes estimés par ces méthodes d'approximation, qui font remonter leurs origines à l'Antiquité.

10 KEY OFF
20 SCREEN 9:COLOR 15:CLS
25 R=0:H=0:S=0
29 COLOR 1: PRINT "Programme d'approximation du cône—basé sur des cylindres empilés":COLOR 15
30 INPUT "Hauteur de chaque cylindre utilisé pour approximation du cône ";H
40 INPUT "Rayon du cylindre inférieur (sera aussi égal à la hauteur du cône) ";R
50 FOR X=0 TO (R/H)
60 S=S+(R-(X*H))^2:PRINT "(";R;"-(";X;"*";H;"))^2 = ";(R-(X*H))^2
70 NEXT X
80 PRINT "Cône réel avec rayon de ";R;"
90 PRINT "L'approximation du même cône est: ";S*H;"PI."
100 INPUT "Un autre? (O ou N)";I$:PRINT:PRINT
110 IF I$="O" OR I$="o" THEN 25