Convertisseur de base

GW-Basic, utilisé par PC-Basic

Programme avec Texte Seulement

PC-BASIC

Dans l'épisode "11001001" de la première saison de Star Trek: The Next Generation, les Bynars, une race d'aliens galactiques réputés pour leur savoir-faire technique, sont amenés à bord de l'Enterprise pour mettre à niveau les systèmes informatiques du vaisseau, mais l'équipage réalise rapidement que les aliens ont leur propre ordre du jour.

 Mais mettez tous ces trucs narratifs de côté. Si vous êtes comme moi, alors la seule question pressante qui vous restera après avoir vu l'épisode est : Quel est le titre de l'épisode réécrit en décimal ?

Bien sûr, le décimal n'était pas la première incursion des humains dans les systèmes numériques. Les anciens Égyptiens avaient un système de numération, tout comme les anciens Babyloniens.

Les Romains sont célèbres pour leurs chiffres romains, qui sont encore utilisés aujourd'hui pour des choses telles que des cadrans d'horloge fantaisistes. Mais le système de numération hindou-arabe a prévalu pour trois raisons, selon Charles Petzold, auteur de Code: The Hidden Language of Computer Hardware and Software :

1. Il n'y a pas de symbole spécial pour 10;

2. La position du chiffre compte autant que la quantité qu'il exprime; et

3. La présence du chiffre zéro, qui est utilisé comme espace réservé.

Les ordinateurs sont des machines binaires, donc la base 2 est le pain quotidien d'un ordinateur; binaire est le système de numérotation le plus simple possible, utilisé pour de nombreuses applications du monde réel telles que les codes-barres UPC.

Les êtres humains, bien sûr, ne sont pas des utilisateurs naturels de la base 2 - principalement parce que la plupart d'entre nous n'ont pas que deux doigts - et la conversion entre la base 2 (binaire) et la base 10 (décimal), dans les deux sens, est fastidieuse et chronophage.

Le plus grand nombre possible que vous pouvez afficher en utilisant uniquement vos doigts ? Si vous levez tous vos doigts, c'est 10 en décimal, mais 1111111111 en binaire (1023 lorsqu'il est reconverti en décimal).

Le mieux est de s'appuyer sur un algorithme informatique pour rendre les conversions à la fois faciles et rapides. Mais avant de pouvoir construire un tel algorithme, nous devons d'abord comprendre le processus de conversion mathématique entre les bases.

Rappelons tout d'abord le fonctionnement des espaces réservés décimaux. Chaque chiffre décimal représente une certaine puissance de 10. Considérez le nombre 2461, qui est:

= 2x10³+4x10² +6x10¹ +1x10⁰

Dans la même veine, les nombres binaires sont construits à partir de puissances de 2 plutôt que de puissances de 10. Par exemple, considérons le nombre binaire 1010100₂ (l'indice indique la base). Chaque chiffre binaire représente un espace réservé pour une puissance de 2 :

= 1x2⁶ + 0x2⁵ + 1x2⁴ + 0x2³ + 1x2² + 0x2¹ + 0x2⁰ =84

Ainsi, 1010100₂ converti en base 10 est égal à 84₁₀.

Notez que toute puissance décimale de deux se traduira automatiquement par un nombre binaire de 1 suivi de zéros, car lors de la conversion de chiffres binaires en décimal, seul le plus élevé la puissance de deux est multipliée par 1, tandis que toutes les puissances décroissantes de deux sont multipliées par zéro.

Il est plus facile de convertir un nombre de base 2 en base 10 que l'inverse. Étant donné que lorsque nous travaillons en binaire, nous ne comptons que par deux avant de déplacer une valeur de position vers la gauche, les nombres binaires ont tendance à être plus longs que leurs nombres décimaux associés.

Nous devrons tenir compte des restes, qui peuvent devenir désordonnés. Reconsidérez 84₁₀; nous devons déterminer combien de fois 2 se divise dans le nombre - puis nous devons diviser 2 en ce quotient, et ainsi de suite, jusqu'à ce que le quotient soit 0. Les restes - qui ne peuvent être que 0 ou 1 - des nombreuses divisions forment le chiffres binaires de la conversion de base de 84₁₀, mais dans l'ordre inverse :

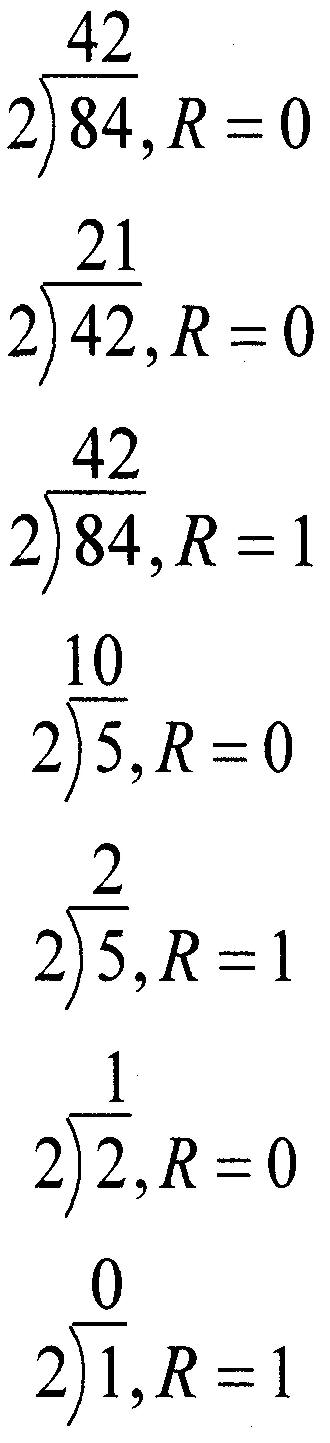
Notez que ces règles s'appliquent également, avec quelques modifications, à toutes les conversions de base.

Et, après avoir exécuté BASE.BAS, vous pourrez enfin décoder la signification décimale de l'épisode "11001001" de Star Trek.

Le nombre que vous entrez pour convertir est stocké sous la forme d'une variable de chaîne appelée NUMBER$; les variables de chaîne, plutôt que numériques, permettent une manipulation caractère par caractère plus facile à l'aide de fonctions telles que LEN, qui calcule la longueur de la chaîne, et MID$, qui permet l'extraction de sous-chaînes.

Pour obtenir des restes, BASE.BAS utilise la fonction INT, coupant la composante fractionnaire du quotient; voir ligne 240 pour les détails.

Bien que le programme fonctionne parfaitement avec les conversions de décimal en binaire et inversement, il présente de nombreux problèmes avec des conversions de base plus non conventionnelles, telles que de la base 7 à la base 4 ou de la base 8 à la base 9. Appelé octal (0-7, 8 chiffres); compter avec octal ressemble à ceci : 0, 1, 2, 3, 4, 5, 6, 7, 10 (puisque nous avons manqué de symboles uniques), 11, 12, 13, 14, 15, 16, 17, 20,. ...

Améliorer le programme signifie supprimer ces problèmes, et peut-être même écrire du code pour les conversions hexadécimales (base 16). Notez que GW-BASIC a une fonction, appelée HEX$, qui convertit le décimal en hexadécimal.

Exemple pour la fonction HEX$

10 CLS:P=0
20 FOR X= 32 TO 255
25 IF P=60 THEN P=0
30 PRINT TAB(P)X;"HEX= "HEX$(X);
35 P=P+15
40 NEXT X

5 REM BASE.BAS
10 KEY OFF
20 CLS
30 PRINT "CONVERTISSEUR BASE À BASE -- POUR BASES 2 à 10"
40 PRINT:INPUT "SUR QUELLE BASE EST VOTRE CHIFFRE (BASE 2 A 10)";BASEIN
45 IF BASEIN<2 OR BASEIN>10 THEN 40 ELSE 50
50 INPUT "EN QUELLE BASE SOUHAITEZ-VOUS CONVERTIR (BASE 2 A 10)";BASEOUT
55 IF BASEOUT<2 OR BASEOUT>10 THEN 50 ELSE 60
60 PRINT "EN BASE ";BASEIN;", QUEL EST VÔTRE NOMBRE";:INPUT NUMBER$
70 IF BASEIN=BASEOUT THEN PRINT"EN BASE ";BASEOUT;", VOTRE NOMBRE EST ";NUMBER$:END
90 PRINT
110 LENGTH=LEN(NUMBER$)
120 IF BASEIN<BASEOUT THEN 130 ELSE 200
130 FOR T=(LENGTH-1) TO 0 STEP -1
140 SUM=SUM+VAL(MID$(NUMBER$,T+1,1))*BASEIN^(POWER)
145 POWER=POWER+1
150 NEXT T
160 PRINT "EN BASE ";BASEOUT;", Votre Nombre est "; SUM
170 END
200 INDEX=1:DIVIDEND=VAL(NUMBER$)
205 DIM DIGITS(30)
210 WHILE DIVIDEND>0
230 QUOTIENT=INT(DIVIDEND/BASEOUT)
240 REMAINDER=BASEOUT*(DIVIDEND/BASEOUT-INT(DIVIDEND/BASEOUT))
245 DIGITS(INDEX)=CINT(REMAINDER) 'LA FONCTION CINT ARRONDI LE NOMBRE
250 INDEX=INDEX+1
260 DIVIDEND=QUOTIENT
270 WEND
280 PRINT "EN BASE ";BASEOUT;",VOTRE NOMBRE EST";
290 FOR T=(INDEX-1) TO 1 STEP -1
300 PRINT DIGITS(T);
310 NEXT T
320 END