Trouver des dérivés

GW-Basic, utilisé par PC-Basic

Programme avec Texte Seulement

PC-BASIC

Utiliser des dérivées est une opération fondamentale en calcul. Une dérivée d'une fonction est son taux de variation, ou sa pente, par rapport à une variable.

Il est simple de trouver la pente d'une fonction linéaire, qui représente une ligne droite, puisque la pente - la montée / course, ou les unités y parcourues (rise) divisées par les x unités parcourues (run) lors de la construction de la ligne - est constante partout sur une ligne.

Si nous avons deux points uniques sur une ligne, (x1, y1) et (x2 ,y2), la pente peut être trouvée en utilisant la formule:

Mais que se passe-t-il si notre fonction n'est pas linéaire ? Peut-on encore trouver sa pente ?

Avec quelques réserves, la réponse est oui. La clé est d'examiner des segments de plus en plus petits de la fonction:

À savoir : les discontinuités, les arêtes vives et certains types de points d'inflexion, car une ligne tangente ne peut être correctement tracée à aucun de ces points.

Sans ligne tangente - une ligne calculant la pente de ces segments étroitement délimités. En utilisant Δ (prononcé "delta") pour représenter une petite quantité, et en réécrivant la formule de la pente, on obtient:

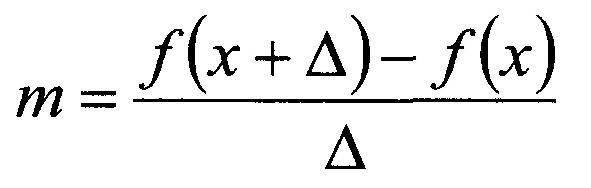
qui trouvera la pente d'une fonction sur un intervalle de taille Δ.

Plus Δ est petit, mieux c'est.

Mais à quel point Δ doit-il être petit ?

Il ne peut certainement pas être nul, puisque Δ est au dénominateur de l'équation de la pente. Au lieu de cela, les mathématiciens utilisent le concept de limite pour "s'approcher" d'une valeur - dans ce cas zéro - aussi près que possible.

La réécriture de la formule de la pente avec une notation limite donne :

Cette limite particulière est formellement appelée la définition de la dérivée.

Prenons un exemple. Le dérivé de:

f(x) = 4x²

peut être obtenu en branchant la fonction fx) dans la définition de la limite :

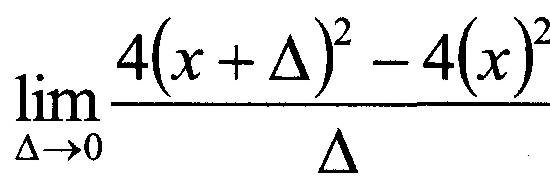
qui "touche" à peine la fonction en un point précis - vous ne pouvez pas déterminer la pente ou le signe de la pente en un point d'intérêt.

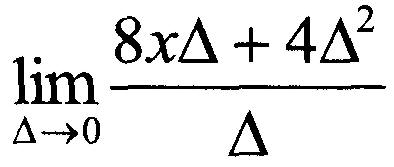
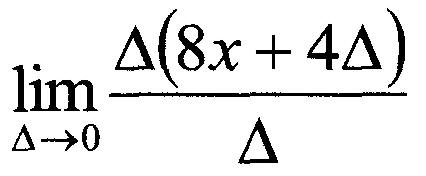
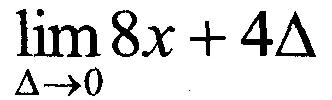
Cette limite simplifiée est facile à trouver : il suffit de mettre zéro pour Δ .* Ainsi:

Les notations f prime et df/dx signifient toutes deux une dérivée première de la fonction f(x). La pente de f(x) n'est pas un nombre fixe, mais change en fonction de la valeur de x.

Prenez X = 6, par exemple. La pente de f(x) en X — 6 est f'(6) = 8 x 6 = 48 . Ainsi, une droite tangente tracée en (6,f(6)) sur un graphe de f(x) a une pente de 48.

Notez que nous n'avons pas pu avoir zéro jusqu'à la simplification finale car delta était logé dans le dénominateur de la limite - nous aurions donc toujours tenté de diviser par zéro, toujours un non-non mathématique.

Cependant, l'utilisation de la définition de la dérivée peut entraîner beaucoup de travail de simplification. La même dérivée de f(x) aurait également pu être trouvée en multipliant simplement l'exposant par le coefficient (ici, en multipliant deux par quatre) puis en soustrayant un de l'exposant.

Notez que f(x) est un monôme ; parce que les dérivés des monômes des variétés garden sont relativement simples à obtenir, un programme informatique, comme DERIVE.BAS, peut facilement modéliser le processus mathématique. (Bien que, techniquement, les exposants entiers négatifs empêchent la fonction d'être un monôme, le programme peut également trouver des dérivées de ces fonctions.)

Lorsqu'il est exécuté, le programme DERIVE.BAS vous demande un monôme sous la forme k*x^n, où k est le coefficient et n est la puissance (les deux valeurs doivent être des nombres entiers), puis affiche sa dérivée.

Plusieurs instructions conditionnelles gèrent les cas particuliers (voir lignes 36 à 38) mais, sinon, les calculs sont très simples ici.

5 KEY OFF:SCREEN 9:COLOR 15,0:CLS
7 PRINT"Trouver des dérivées simples\"
10 LOCATE 4,5:PRINT"Entrer une fonction en utilisant ce format: K*x^n":PRINT
15 PRINT"Veuillez utiliser uniquement des nombres entiers pour les valeurs de K et n":PRINT
20 INPUT "Quelle est la valeur de K ";K
30 INPUT "Quelle est la valeur de n";N
35 NW=N-1
36 IF NW=0 THEN 60
37 IF NW=-1 THEN 45
38 IF NW=-1 THEN 65
39 IF NW<-1 THEN 55
40 PRINT "d/dx(";K;"x^";N;") = ";K*N;"x^";NW
43 END
45 PRINT "d/dx(";K;"x^";N;") = ";K*N;" x"
50 END
55 PRINT "d/dx(";K;"x^";N;") = ";K*N;"/ x^ ";-(NW)
57 END
60 PRINT "d/dx(";K;"x) = ";K*N
63 END
65 PRINT "d/dx(";K;"= ";0
70 END

Bien que le défi puisse être apparent, il est incroyablement difficile à relever : écrire un programme pour trouver la dérivée de n'importe quelle fonction (si une telle dérivée peut être obtenue).

Différentes classes de fonctions nécessiteraient leurs propres algorithmes de calcul de dérivées : outre les monômes, les fonctions polynomiales, exponentielles, trigonométriques et hyperboliques ne sont que quelques-unes des nombreuses classes de fonctions possibles à prendre en compte.

De plus, des procédures étape par étape pour gérer les règles du produit, du quotient et de la chaîne devraient être écrites. La tâche, bien que redoutable en raison du grand nombre de permutations de fonctions, n'est pas impossible pour l'intrépide programmeur GW-BASIC.