Factorisation des trinômes
GW-Basic, utilisé par PC-Basic
Programme avec Texte Seulement
PC-BASIC
Les trinômes sont des polynômes de la forme ax² + bx + c , où a ≠ 0. Pour simplifier, nous ne considèrerons que les trinômes factorisables où a > 0. De plus, les trinômes produisant des facteurs imaginaires ne seront pas traités ici.
Mais comment déterminer si un trinôme a des facteurs entiers ?
Rappelons la formule quadratique, qui se trouve en complétant le carré sur ax² + bx + c = 0 :
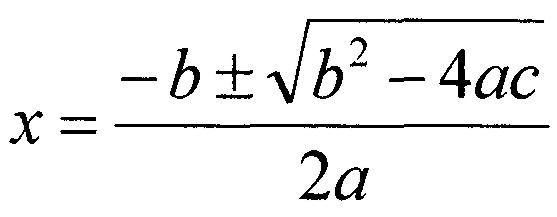
La formule quadratique permet de trouver les solutions d'un trinôme, que ce trinôme soit factorisable ou non. On s'intéresse au radicante de la formule quadratique : b - 4ac.
Ce radicante est appelé le discriminant. Si le discriminant est négatif, alors les solutions sont imaginaires ; si le discriminant est nul, alors les solutions sont toutes les deux X = -b/2a ; et si le discriminant est positif, il y a deux cas à considérer :
1. Le discriminant est un
carré parfait ; ou
2. Le discriminant n'est pas
un carré parfait.
Si le discriminant est un carré parfait, le radical disparaîtra, laissant deux solutions rationnelles. Mais si le discriminant n'est pas un carré parfait, le radical reste en place, laissant deux solutions irrationnelles.
Seules les solutions rationnelles conduisent à des trinômes factorisables, nous ne considèrerons donc que des discriminants au carré parfait.
Nous pouvons en outre résumer les trinômes factorisables en deux types :
1. Trinômes de
coefficient 1 devant x² de la forme x² + bx + c ; et
2. Trinômes avec un
coefficient entier supérieur à 1 devant le x² .
Pour le premier type, vous devrez trouver deux nombres qui totalisent le coefficient du deuxième terme (appelé le terme linéaire) du trinôme et multiplier au troisième terme (appelé le terme constant) du trinôme.
Ensuite, vous remplissez (x + ___)(x +____) avec ces deux nombres.
Par exemple, x -6x-40, lorsqu'il est factorisé, devient (x-10)(x+4) puisque -10 ajouté à 4 est -6 et -10 multiplié par 4 est 40.
Pour le deuxième type de trinôme factorisable, vous aurez besoin de trouver deux nombres qui totalisent le coefficient du second terme (appelé le terme linéaire) du trinôme mais qui se multiplient également par le produit du premier terme (appelé le coefficient dominant) et troisième terme (appelé terme constant) du trinôme.
Après avoir trouvé ces deux termes, un nombre rationnel peut être écrit sous la forme d'une fraction ou sous la forme d'un nombre décimal répétitif ou final.
Un nombre irrationnel ne peut pas être écrit sous forme de fraction ; son expansion décimale est sans fin, chaque chiffre étant imprévisible en fonction de ceux qui l'ont précédé.
Vous allez réécrire le trinôme en remplaçant le moyen terme par les deux termes que vous avez trouvés ci-dessus, puis factoriser l'expression en regroupant.
Par exemple, pour factoriser 2x²-7x+6, vous devez d'abord trouver deux termes dont la somme est -7 et également multiplier par 12 (douze est le produit du coefficient principal et du terme constant). Les nombres -3 et -4- satisfont ces conditions.
Nous pouvons réécrire le polynôme sous la forme 2x²-3x-4x+6 et le factoriser en regroupant les termes :
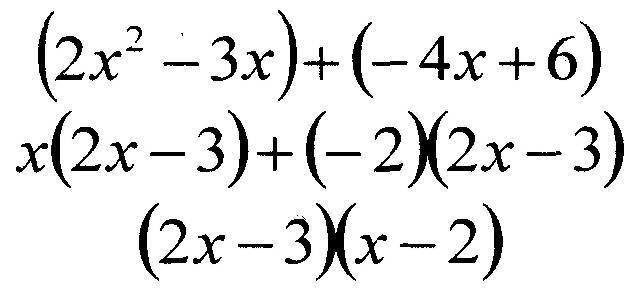
Il existe une alternative plus visuelle à la factorisation des trinômes avec un coefficient autre que 1 devant le x²; c'est ce qu'on appelle la méthode X. Factorisons à nouveau 2x² -7x + 6, cette fois en utilisant la méthode X.
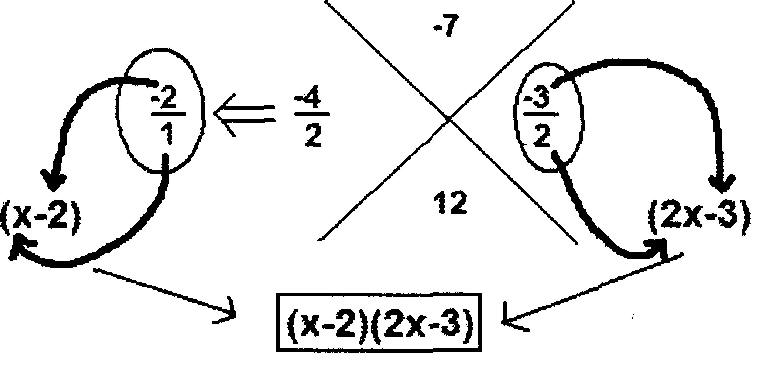
Le X au centre du diagramme divise votre espace de travail en quatre quadrants. Le nombre supérieur (-7) est le coefficient devant le terme x du polynôme, qui est -7.
Le nombre dans la partie inférieure du X est le premier terme du polynôme multiplié par le dernier terme du polynôme (ainsi, 2 multiplié par 6 donne 12).
Ensuite, trouvez deux nombres qui se multiplient pour vous donner 12 et additionnez-les pour vous donner -7 - ces deux nombres sont, bien sûr, -4 et -3, donc -4 et -3 sont placés de chaque côté du X.
Divisez ces deux nombres par le coefficient devant le terme x² (qui est 2), puis réduisez les fractions. Les fractions réduites sont encerclées dans le diagramme.
Les dénominateurs des fractions réduites sont les coefficients devant x dans les binômes qui factorisent le trinôme, tandis que les numérateurs des fractions réduites sont les termes constants des binômes.
Après avoir entré votre trinôme, le programme trouve le discriminant sur la ligne 100 ; pas besoin de chercher inutilement dans des combinaisons d'entiers s'il n'y en a pas à trouver.
Ensuite, deux boucles FOR/NEXT recherchent des paires d'entiers, ne s'arrêtant que s'ils s'ajoutent au terme linéaire du trinôme et correspondent également au produit du coefficient principal du trinôme et du terme constant.
Le reste du programme réduit les facteurs, trouvés à l'aide de la méthode X détaillée ci-dessus, en recyclant l'algorithme FACTOR.BAS.
Le problème majeur avec le programme est la vitesse - lorsque les coefficients augmentent, l'algorithme s'exécute plus lentement. Une recherche par force brute à travers les facteurs possibles n'est pas particulièrement efficace et entrave gravement l'utilité du programme.
Par exemple, essayez de factoriser 20x²-3x-35. Vous allez attendre longtemps la réponse.
Outre la vitesse, l'autre problème avec FACTOR.BAS est la portée : pourquoi sommes-nous limités uniquement aux trinômes ?
Il existe des classes entières d'autres polynômes factorisables similaires que GW-BASIC serait bien adapté pour aborder. Mettez-vous au travail.
