Matrice
GW-Basic, utilisé par PC-Basic
Programme avec Texte Seulement
Travail sur les matrices
Les matrices sont des arrangements rectangulaires de nombres (ou de variables) en lignes et en colonnes, et en mathématiques sont très utiles pour organiser des données ainsi que pour résoudre des équations.
Par exemple, supposons que vous vouliez résoudre ce système d'équations :
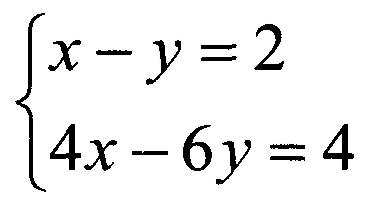
Mise en place d'une équation matricielle, comme indiqué ci-dessous,

vous met en position d'isoler la matrice x-y d'un côté, ce qui résout finalement les deux variables :
Bien que l'utilisation de matrices ne soit pas particulièrement difficile, de nombreux calculs les impliquant sont assez fastidieux.
Par exemple, pour trouver une matrice inverse (notée par l'exposant -1 dans l'équation ci-dessus) qui est de deux lignes sur deux colonnes, vous devrez d'abord trouver ce qu'on appelle le déterminant - calculé uniquement à partir d'une matrice carrée, le déterminant est une valeur qui révèle certaines propriétés de la matrice, comme si elle est singulière ou non, puis transpose et inverse les signes des autres éléments de la matrice. (Trouver le déterminant d'une matrice de trois lignes sur trois colonnes est vraiment fastidieux.)
Les algorithmes informatiques fonctionnent généralement bien lorsque les étapes d'une procédure (surtout mathématique) sont non ambigües et exhaustives. C'est le cas des opérations matricielles abordées par la MATRICE.
Le programme MATRIX.BAS ci-dessous. En plus de trouver des inverses et des déterminants simples, le programme permet également la transposition (transformation des lignes en colonnes et des colonnes en lignes).
Il n'y a pas de lignes de code compliquées ici; une fois que les éléments de la matrice sont entrés, tout n'est qu'un travail fastidieux, juste plug-and-chug, et GW-BASIC s'acquitte bien encore une fois en tant que calculatrice programmable.
Le programme pourrait être rationalisé un peu sans perdre aucune de ses fonctionnalités. Par exemple, un seul sous-programme doit être consacré à l'entrée dans une matrice, et les éléments de la matrice doivent se voir attribuer des valeurs dans le cadre d'un tableau, plutôt que d'avoir leurs propres variables séparées (comme A, B, C, etc. , car le programme est maladroitement écrit maintenant). De cette façon, plus de flexibilité serait permise et des opérations matricielles plus difficiles pourraient être effectuées.
