Simplifier les radicaux

GW-Basic, utilisé par PC-Basic

Programme avec Texte Seulement

PC-BASIC

Lorsque vous êtes confronté à √8 , qui n'a pas de solution entière, vous pouvez être tenté de simplement taper l'expression dans une calculatrice. La calculatrice rapportera consciencieusement : 2,8284....

Mais une expansion décimale ne simplifie pas l'expression, parce que √8 est un nombre irrationnel - qui ne peut pas être écrit comme un décimal de fin ou de répétition (ou une fraction).

Ainsi, simplifier une racine carrée telle que √8 consiste à trouver le plus grand carré parfait qui soit un facteur du radicante (le nombre à l'intérieur du signe radical √ ). Le plus grand facteur carré parfait est 4, puisque 4 se divise en 8 de manière égale.

La suppression du carré parfait nous laisse avec un radicante de 2, qui est le quotient de 8 et 4 :

Notez que 2√2 peut s'écrire de manière équivalente en utilisant un exposant fractionnaire au lieu d'un signe radical : 2 • 2½ .

En utilisant la même logique, nous pouvons simplifier d'autres types de radicaux en plus des racines carrées. Par exemple, considérons le ³√54 , lu comme la racine cubique de 54. Puisqu'il n'y a pas d'entier multiplié par lui-même deux fois égal à 54, ³√54 aura également une expansion décimale non répétitive et non terminale.

Cependant, l'expression peut être simplifiée en factorisant le plus grand cube parfait possible qui se divise uniformément en 54 :

La même procédure de base fonctionne pour simplifier d'autres radicaux avec des radicantes entiers et des indices de nombres entiers.

Après avoir entré le radicante entier et l'indice de nombre entier, le programme détermine d'abord la plus grande puissance d'indice parfait possible (carré, cube, quatrième, etc.) pour potentiellement factoriser le radicante (voir les lignes 60 à 80), et puis divise à plusieurs reprises pour trouver le plus grand facteur de puissance d'indice parfait (à partir de la ligne 100).

Veuillez noter à quel point la fonction INT s'avère utile ici ; la fonction INT supprime ou tronque tous les chiffres après la virgule. Donc, si le quotient des nombres a et b est égal au quotient tronqué de ces deux mêmes nombres, alors b se divise uniformément en a et est donc un facteur de a.

Écrire ce programme, et bien d'autres, sans recourir à la fonction INT serait très difficile.

L'indice du radical détermine sa racine. Pour les racines carrées, l'indice implicite est 2 ; pour les racines cubiques, l'indice est 3, écrit à côté du signe radical ; pour les quatrièmes racines, l'indice est 4 ; etc.

10 KEY OFF:CLS
15 COUNTER=2
20 PRINT"--- SIMPLIFY RADICALS (WITH INTEGER RADICANDS ---"
25 INPUT"WHAT IS THE RADICAL'S INDEX (2 - SQUARE ROOT)";INDEX
27 IF INDEX<>INT(INDEX) THEN 25
28 IF INDEX<2 THEN 25
30 INPUT"WHAT IS THE INTEGER RADICAND INSIDE THE RADICAL";RAD
40 IF RAD<>INT(RAD) THEN 30
50 'Find the biggest perfect [index-power] which is not greater than the radicand/2
60 WHILE COUNTER^INDEX<=RAD
70 COUNTER=COUNTER+1
80 WEND
90 COUNTER=COUNTER-1 'Resets to the correct number
100 'Now search for the biggest perfect [index-power] which is a factor of the radicand
110 'and divide out that factor, simplifying the radical
120 FOR X=COUNTER TO 1 STEP -1
130 IF RAD/X^INDEX=INT(RAD/X^INDEX) THEN 150
140 NEXT X
150 PRINT"The simplified radical of (";RAD;")^l/" INDEX;" is:"
155 PRINT
160 IF RAD/X^INDEX<>1 AND X<>1 THEN PRINT X;"*(";RAD/X^INDEX;")^l/";INDEX
170 IF RAD/X^INDEX=1 AND X<>1 THEN PRINT COUNTER
175 IF X=1 THEN PRINT "(";RAD;"')^l/";INDEX
180 PRINT:PRINT:PRINT
190 END

RADICAL. BAS, tel qu'il est codé maintenant, ne simplifie pas toujours complètement un radical. Bien qu'il gère facilement les simplifications les plus simples, telles que tourner ³√320 en 4³√5 — les autres radicaux ne s'en sortent pas aussi bien. Par exemple, considérons ⁶√512 .

RADICAL.BAS le simplifie en 2 x 8^1/6, ce qui semble logique à première vue. Cependant, notez que 2 x 8^1/6 peut être réécrit un peu, résultant en une forme plus simple :

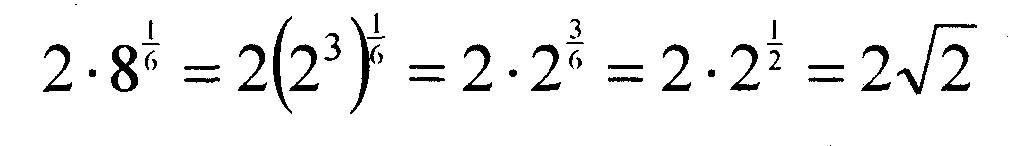
Reconnaître quand ces sortes de manipulations mathématiques s'appliquent vous tiendra très occupé dans votre quête pour améliorer le programme.