Notion sur le calcule des roulements

Notion sur le calcule des roulements

Sous charge et au cours du mouvement de rotation les chemins des bagues de roulements reçoivent de la part des éléments roulants, billes ou rouleaux, des millions de compressions élastiques intermittentes. Il en résulte, avec le temps, des fissurations amenant progressivement un écaillage des surfaces. C'est le phénomène de fatigue.

1. Durée de vie normalisée L₁₀

La durée de vie L₁₀ d'une série de roulements identiques, soumis à la même charge, est égale au nombre de tours, ou de révolutions, réalisés par 90 % des roulements de la série avant qu'apparaissent les premiers signes de fatigue.

Unités : la durée de vie normalisée se calcule en millions de tours, parfois par commodité en heures de fonctionnement.

Remarques :

-La fatigue est un phénomène aléatoire ou statistique. Autrement dit, des roulements identiques, de mêmes dimensions, de mêmes matériaux, appartenant à un même lot, tous chargés de la même façon, auront, après le même essai, des durées de vie différentes.

-L₁₀ est la durée de vie (moyenne statistique) basée sur une fiabilité de 90 %, c'est-à-dire 90 % de survie après essai sur un même lot. L₁₀ sert de référence à tous les roulements de la série.

2. Durée de vie corrigée Ln : fiabilité différente de 90 %

Si l'on désire obtenir une durée de vie L_n supérieure à L₁₀, ou à une fiabilité supérieure, celle-ci peut être obtenue par L_n = a_1.L₁₀ avec a₁ = 4,48 [ln(100/F)]^2/3 ; avec F = fiabilité en %.

Remarques :

L₅₀ = 5L₁₀.

- La durée de vie moyenne (fiabilité de 50 %) d'un lot L₅₀ est égale à environ 5 fois la durée L₁₀. Elle est de 15.L10 avec 10 % de survie.

-En pratique on utilise L_n = a₁.a₂-a₃.L₁₀

L'étude des coefficients correcteurs a2 (liée à la géométrie et à la matière du roulement) et a3 (fonction des conditions de fonctionnement : lubrification...) sort du cadre de cet ouvrage. Dans certains cas parfaitement bien maîtrisés, la durée de vie peut devenir infinie.

3. Fiabilité F et probabilité de défaillance D (L < L10)

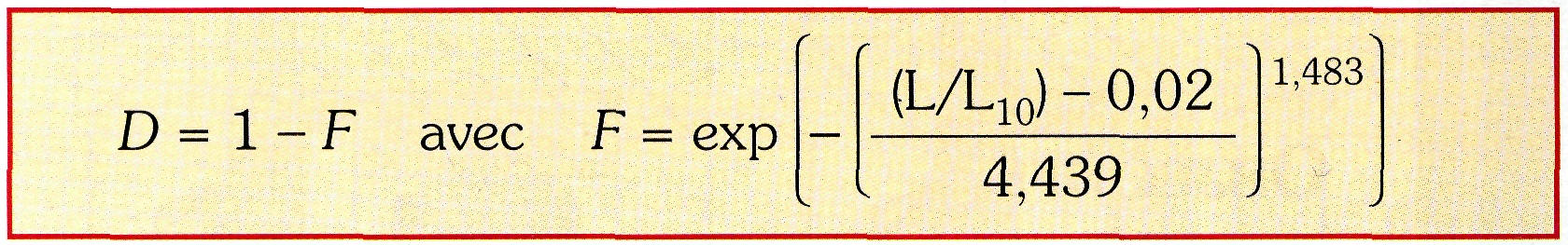
Exemple :

la durée de vie prévue d'un roulement est L₁₀ = 10 000 heures. On souhaite connaître la fiabilité après 5 000 heures de fonctionnement juste avant extinction de la garantie commerciale.

L = 5 000 et L/L₁₀ = 5 000/10 000 = 0,5

L'équation précédente donne F = 0,963 7 (fiabilité de 96,37 %)

Pourcentage de défaillance : D = 1 - F = 0,036 3 (3,63 %).

4. Durée de vie d'un ensemble ou d'une association de roulements

Lorsqu'un ensemble de roulements (E) comprend plusieurs roulements fonctionnant en même temps (exemple : arbre avec plusieurs roulements), la durée de vie LE10 de l'ensemble est fonction de la durée de vie Lj 10 de chacun des n roulements. Elle est définie par la relation suivante :

Exemple : deux roulements à rouleaux coniques d'un même arbre ont des durées respectives de 15 000 et 25 000 heures. Calculons la durée de vie probable du montage.

Cette durée est toujours inférieure à la plus petite des valeurs L{ 10, ici 15 000 heures.

II - Capacité de charge dynamique C

En dépit de l'utilisation d'aciers spéciaux très résistants, les roulements ont une durée de vie limitée. Cette durée dépend principalement de la charge supportée. Plus la charge est faible, plus la durée de vie est longue, et inversement.

Définition : la charge dynamique de base C, d'une série de roulements identiques, est la charge radiale (axiale pour une butée), constante en intensité et en direction, que peut endurer 90 % des roulements du groupe<pendant 1 million de tours, avant qu'apparaissent les premiers signes de fatigue.

Autrement dit, si un lot de 100 roulements identiques est soumis au cours d'un essai à sa charge de base C [Fr = C), 90 roulements du lot (90 %) auront une durée de vie qui atteindra ou dépassera 1 million de tours (L₁₀ = 1).

Remarques :

-La capacité C est une des caractéristiques de base des roulements ; elle est indiquée dans les catalogues des fabricants en même temps que ci, D, B et r.

-Pour une même référence normalisée de roulement, la valeur de C peut varier sensiblement d'un fabricant à l'autre.

III - Relation entre durée de vie L₁₀ et charge dynamique C

L₁₀ = (C/P)ⁿ

L₁₀ : durée de vie du roulement en millions de tours

C : charge dynamique de base

P : charge équivalente exercée sur le roulement (voir paragraphe IV)

n = 3 pour les roulements à billes

n = 10/3 pour les roulements à rouleaux

Durée de vie L10H en heures de fonctionnement

L_10h = L₁₀.10⁶ / 60.N

L10 : millions de tours

N : vitesse de rotation en tr/min.

Exemple : un catalogue de roulements donne, pour un roulement à billes à contact radial, une capacité de charge dynamique C égale à 6 300 daN. Le roulement supporte une charge P de 2 100daN.

Déterminons les durées L₁₀ et L_10H si la vitesse de rotation de l'arbre est de 150 tr/min.

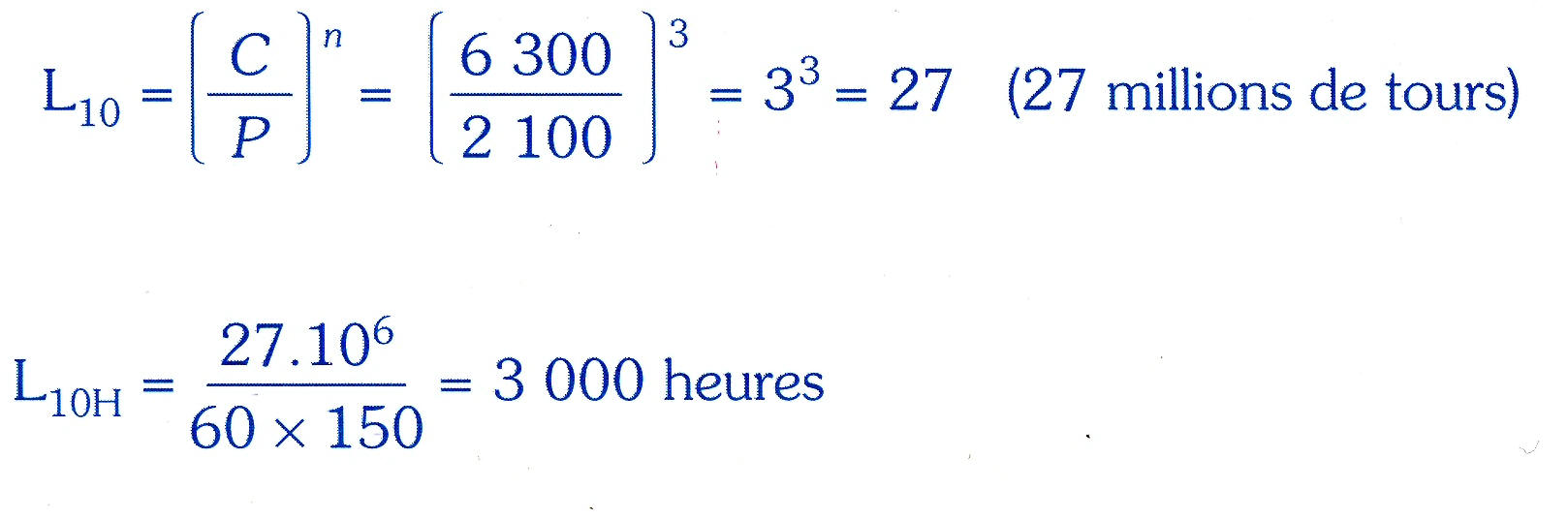
IV - Calcul de la charge dynamique équivalente P

La charge équivalente P est une charge radiale pure, donnant exactement la même durée de vie que la combinaison charge axiale F_a plus charge radiale F_r réellement exercée sur le roulement. P est différent de la charge combinée F.

1. Charge équivalente P et charges exercées F_a et F_r.

1.Cas particuliers

Dans le cas des roulements à aiguilles et des roulements à rouleaux cylindriques avec bagues séparables : F_a = 0 et P = F_r.

Avec des butées ne supportant que des charges axiales : F_r = 0 et P = F_a.


2. Valeur de P dans le cas des roulements à rouleaux cylindriques.	3. Valeur de P dans le cas des butées.

2. Cas général d'une charge combinée

F_a et F_r étant connues, la charge P est calculée à l'aide de la relation :

P = XFr + YFa

X et Y sont des coefficients normalisés liés à la nature du roulement et à ses dimensions (tableau des Valeurs des coefficients X et Y).

Remarques :

- Si la bague extérieure tourne par rapport à la direction de la charge la valeur de P est calculée par :

P=l,2.X.F_r+Y.F_a

- Les relations précédentes sont obtenues à partir des courbes expérimentales d'équidurée.

4. Principe des courbes d'équidurée.

Sous l'action des charges F₁, F₂, F₃ ou F₄ le roulement a la même durée de vie.

La courbe d'équidurée est obtenue en traçant la courbe passant par les extrémités des charges précédentes, toutes tracées à partir du même point d'application O.

Cette courbe est ensuite approximée par des droites pour en simplifier l'exploitation (permet de définir les coefficients X, Y, e = tan β...).

V - Capacité de charge statique C₀ et charge statique équivalente P₀

Pour un roulement chargé à l'arrêt, ou dans le cas de mouvements de faible amplitude et de petites oscillations, C₀ représente la charge statique limite à ne pas dépasser. Au-delà de cette charge, les déformations des éléments roulants deviennent inadmissibles.

La plupart des fabricants admettent une déformation maximale admissible égale à 0,0001 du diamètre moyen de l'élément roulant (conformément à l'ISO 76).

C₀ est une grandeur caractéristique du roulement indiquée dans les catalogues de fabricants en même temps que d, D, B, C...

Comme C, C₀ est une charge radiale pure. Si le roulement est soumis à une charge combinée F_a plus F_r, il est nécessaire de calculer au préalable la charge statique équivalente P₀ (analogie avec P).

P₀ = X₀.F_r + Y₀.F_a avec P₀.S₀ ≤ C₀

Remarque : si le roulement est soumis à une charge radiale pure F_r alors P₀=F_r avec P₀.s₀ ≤ C₀.

5. Méthode de calcul ISO.
Pour appliquer la méthode, appeler A le roulement supportant F_a

VI - Calcul des roulements

Données nécessaires : F_a, F_r et N, la vitesse de rotation. La durée de vie L₁₀ dépend de ces paramètres.

Autres paramètres usuels : diamètre minimal d_mini de l'arbre, fourni par la résistance des matériaux, et D_maxi, qui résulte de l'encombrement général et de la place disponible.

Faire le choix d'un type de roulement ou du moins en limiter le nombre.

1. Calculs de vérification

Ils sont destinés à vérifier la durée de vie d'un roulement dont les dimensions {d, D, B, C, C₀, e, Y...) sont connues.

2. Calculs de détermination

L'objectif est de choisir un roulement et ses dimensions connaissant une durée de vie souhaitée. Il est nécessaire de procéder par itération (calculs de vérification successifs à partir de roulements judicieusement choisis) avant d'envisager un choix définitif.

Il existe de nombreux logiciels d'assistance permettant d'effectuer rapidement ce type de calcul.

3. Cas des roulements à contact oblique et à rouleaux coniques

Pour ces roulements, le calcul de la charge axiale F_a présente une différence du fait de la géométrie particulière des bagues. Pour chaque roulement, l'action de la charge radiale F_r entraîne par « effet de cône », la création d'une charge axiale induite (F_ai) s'ajoutant ou se retranchant à celle déjà exercée par l'arbre (F_aE).

Dans la méthode de calcul normalisé ISO, F_ai = 0,5.F_r/Y. Cette méthode permet de calculer les charges axiales totales F_aA et F_aB résultant de F_aE et des charges axiales induites F_ai, puis de déduire les charges équivalentes P_A et P_B. Les autres calculs (L₁₀...) ne sont pas différents de ceux des autres roulements.

4. Exemples

Exemple 1

Un roulement à billes à contact radial de dimensions d = 50, D = 110, B = 27, C = 6 200 daN, C₀ = 3 800 daN, supporte la charge combinée F_a = 400 daN et F_r = 1 000 daN. Quelle durée de vie peut-on attendre si la vitesse de rotation de l'arbre est de 150 tr/min ?

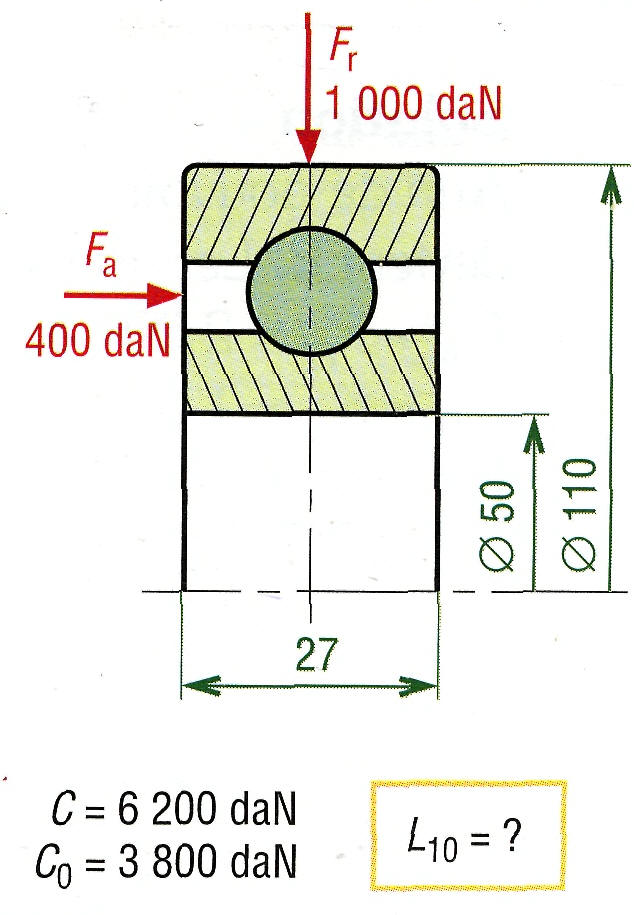
Solution

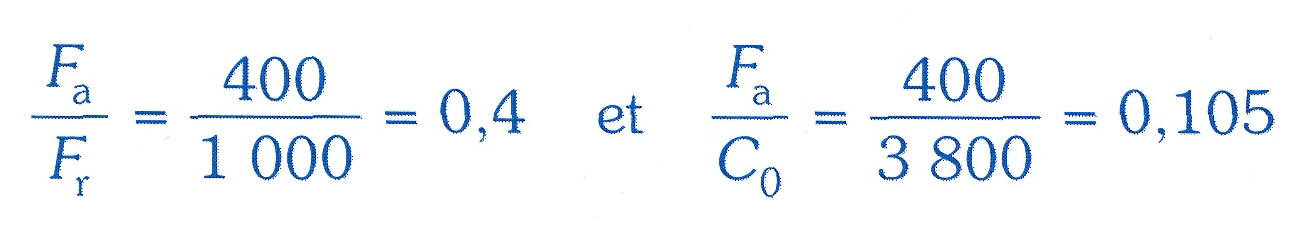
Pour ces roulements les valeurs de e et Y dépendent de la valeur de F_a/C₀.

D'après le tableau page des valeurs des coefficients X et Y : F_a/C₀ = 0,105 est située entre 0,084 et 0,110.

Par correspondance la valeur de e sera située entre 0,28 et 0,30 et celle de Y entre 1,45 et 1,55.

Les valeurs précisent sont obtenues par proportionnalité ou interpolation.

Exemple 2

Déterminer la durée de vie L_10E d'un montage de deux roulements à rouleaux coniques 1 et 2, montés en X, tel que F_r1 = 1 500 daN, F_r2 = 2 000 daN et F_ae = 1 000 daN. L'effort axial F_ae est supporté par le roulement 2.

Dimensions : d = 60, D = 95, B = 27, C = 7 850 daN, C₀ = 7 650 daN, e = 0,33, Y = 1,83 pour le roulement 1

d = 90, D = 140, B = 39, C = 18 600 daN, C₀ = 19 600 daN, e = 0,27, Y = 2,2 pour le roulement 2.

Solution

Afin de pouvoir appliquer la méthode ISO, le roulement 2 est baptisé A et le roulement 1 devient B. Les données deviennent alors :

F_rA = F_r2 = 2 000 daN ; e_A = 0,27 ; Y_A = 2,2 ; C_A = 18 600 daN

F_rB = F_r1 = 1 500 daN ; e_B = 0,33 ; Y_B = 1,83 ; C_B = 7 850 daN

Par la méthode ISO les charges axiales induites sont :

C'est le cas d'application n° 1 de la méthode. Les charges axiales F_a et les charges équivalentes P sur les roulements sont :

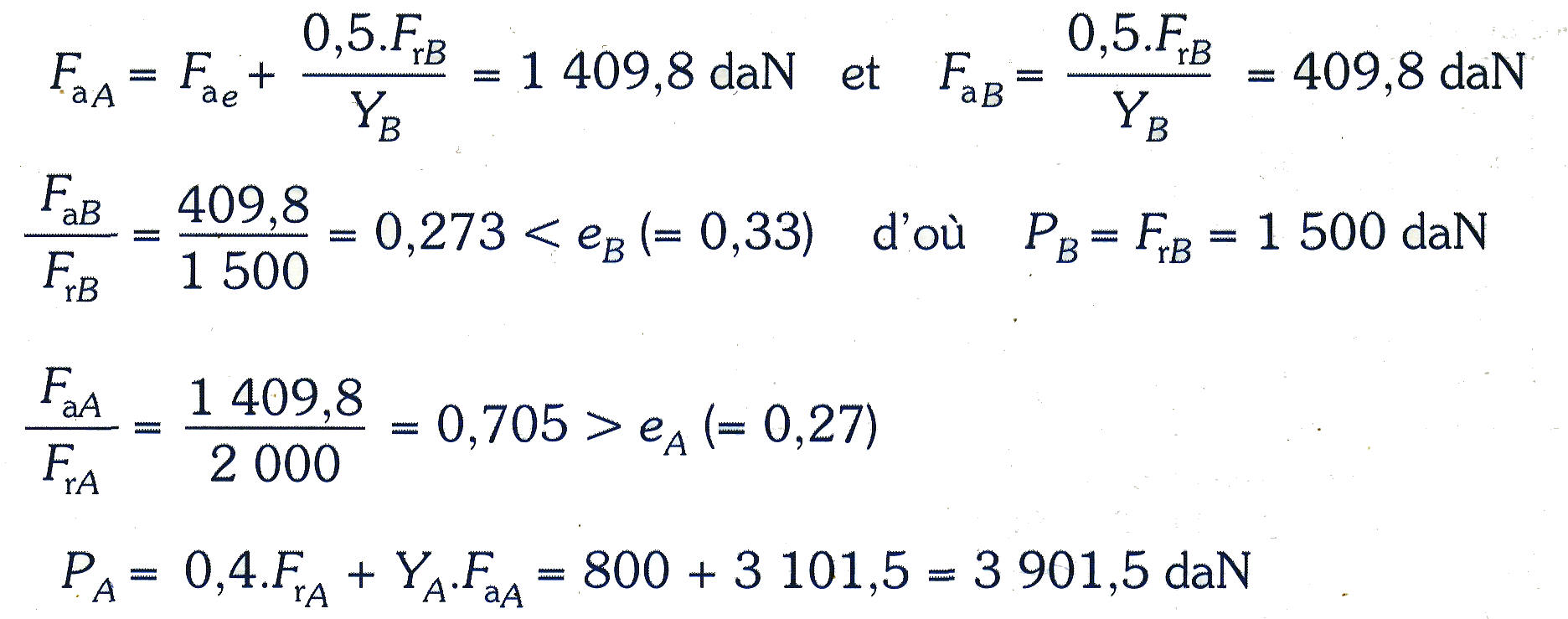
Durées de vie correspondantes :

VII - Exercice

Exercice 1

Reprendre les données de l'exemple 1 avec un roulement à contact oblique à deux rangées de billes, d = 50,D= 110 (voir autres caractéristiques Tableau Roulement à contact oblique). Déterminer la durée de vie du roulement.

Réponse : L₁₀ = 235,3 ; L_{10 H} = 26 146 heures.

Exercice 2

Reprendre les données de l'exemple 1 avec un roulement à rotule sur rouleaux, d = 50, D = 110 (voir autres caractéristiques Roulement à rouleaux cylindriques).

Déterminer la durée de vie du roulement.

Réponse : L₁₀ = 3 197 ; L_10H = 355 240 heures.

Exercice 3

Reprendre les données de l'exemple 2 avec F_rA = 1 000 daN ; F_rB = 900 daN ; F_aE = 400 daN ; N = 500 tr/min ; C_A = 9 500 daN ; e_A = 0,43 ; Y_A = 1,38 ; C_B = 8 190 daN ; e_B = 0,46 ;Y_B= 1,31. Déterminer les durées de vie des roulements et celle de l'ensemble.

Réponse : L_10A = 18 545 heures ; L_10B = 65 550 heures ; L_10E = 16 890 heures.