 |
 |
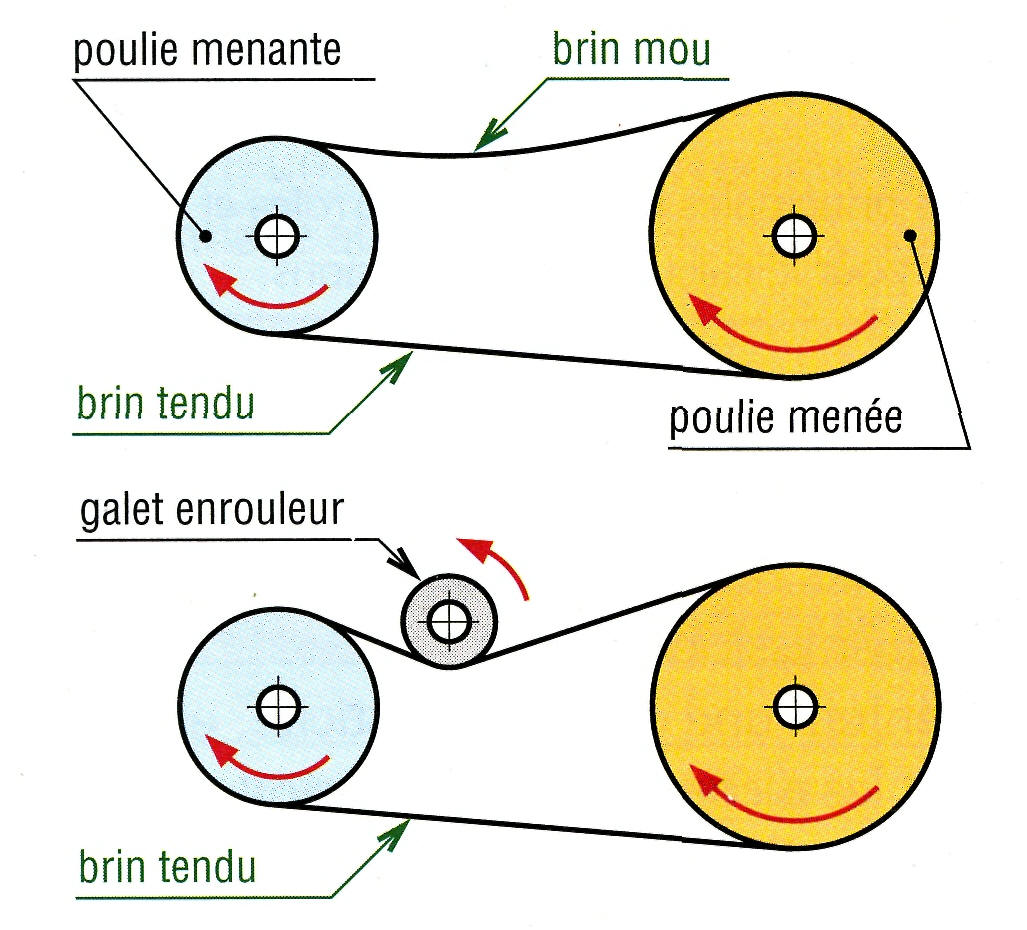
| 1. Principe
d'une transmission par poulie courroie. |
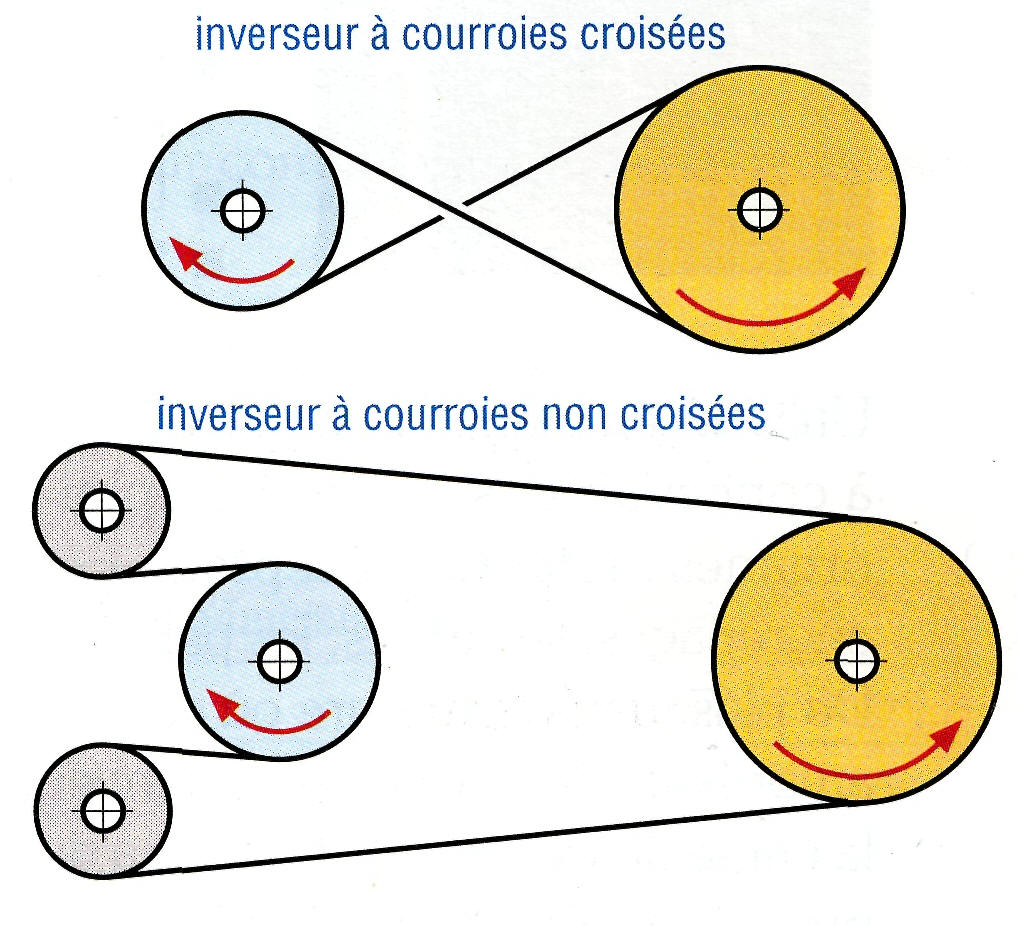
2. Inverseurs. |
I - Transmissions par poulies et courroies
Transmission par courroies et chaînes
Silencieuses, elles sont surtout utilisées aux vitesses élevées avec de grands entraxes possibles entre poulies.
La tension initiale des courroies est indispensable pour garantir l'adhérence et assurer la transmission du mouvement.
Un système à entraxe réglable ou un dispositif annexe de tension (galet enrouleur, etc.) est souvent nécessaire pour régler la tension initiale et compenser l'allongement des courroies au cours du temps.
À l'exception des courroies crantées, en fonctionnement normal, il existe un léger glissement de la courroie sur les poulies amenant une imprécision du rapport de transmission ; celui-ci n'est pas exactement égal au rapport des diamètres des deux poulies.
 |
 |
| 1. Principe
d'une transmission par poulie courroie. |
2. Inverseurs. |
Règle : quand une courroie quitte une poulie elle doit se trouver dans le plan médian de la poulie réceptrice.
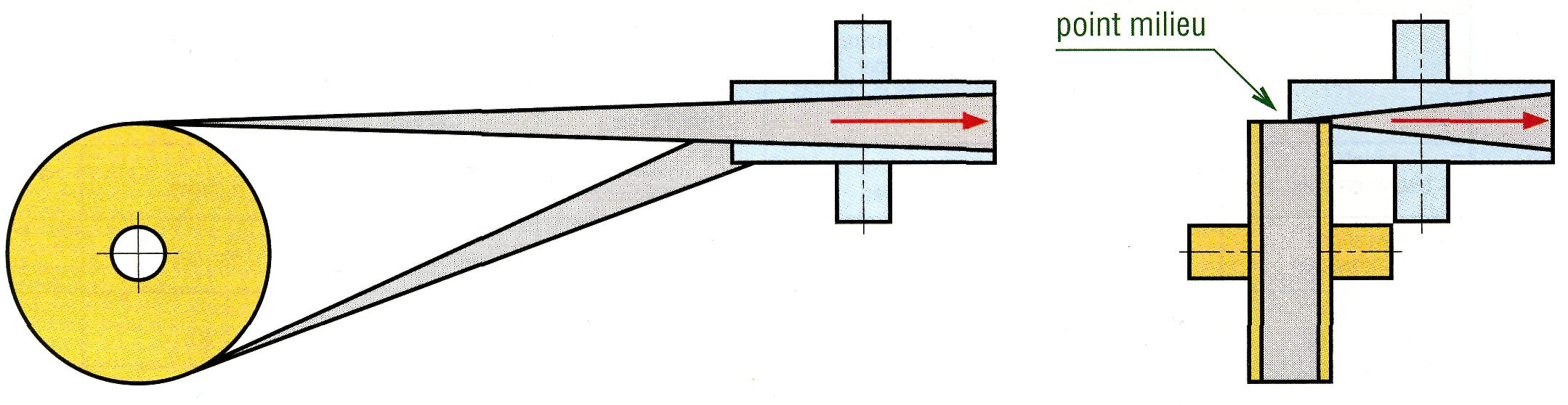
3. Cas d'arbres perpendiculaires.
Courroies rondes : elles sont surtout utilisées dans les petits mécanismes.

4. Courroies rondes :. exemple de configuration.
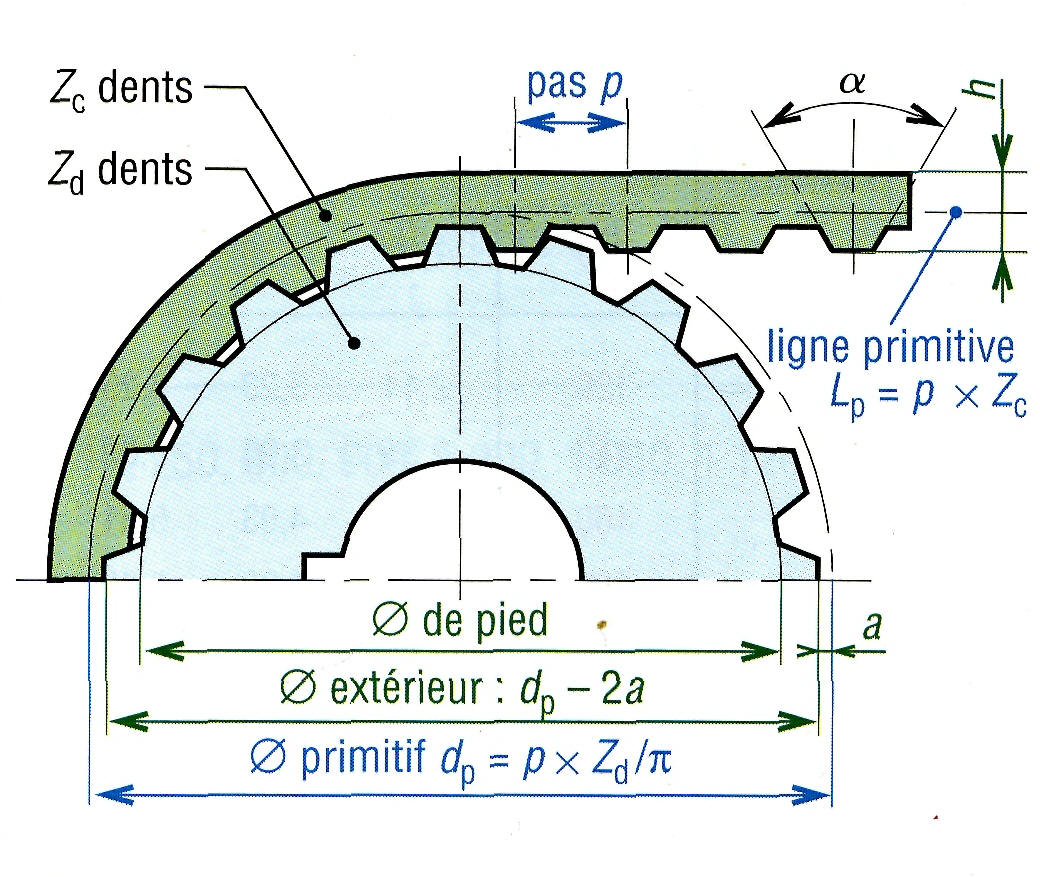
1. Courroies plates
Très silencieuses, elles permettent de grands rapports de réduction et sont surtout utilisées aux grandes vitesses (80 à 100 m/s) sous de faibles couples.
Elles absorbent bien les vibrations torsionnelles, ce qui autorise les grands entraxes et les grandes longueurs. Elles ont un très bon rendement (≈ 98 %, comparable aux engrenages). Le bombé des poulies permet un meilleur guidage et une meilleure stabilité de la courroie et compense dans une certaine mesure un désalignement initial.
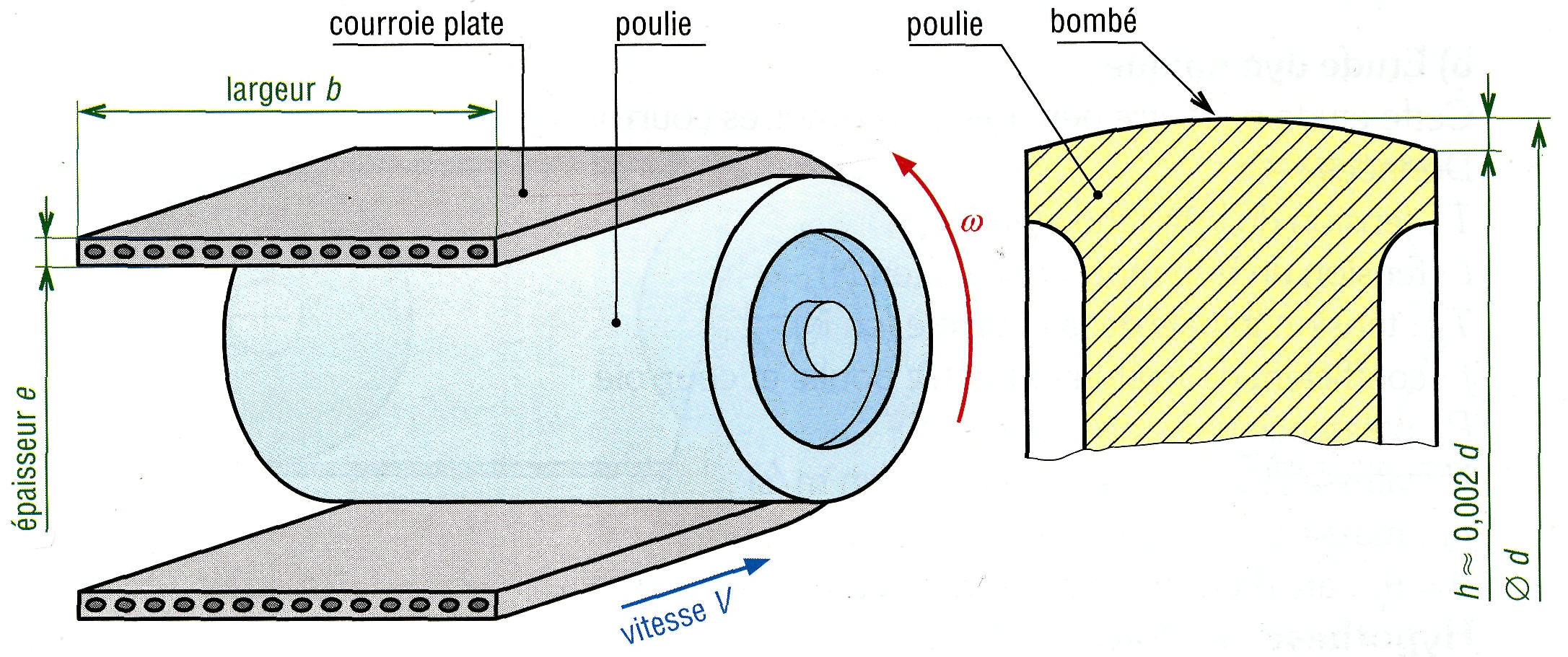
5. Courroie plate. Matériaux :
polyuréthane (< 25 m/s), polyester, aramide revêtu silicone (< 80 m/s)...
a) Rapport de transmission

Nd : vitesse de la petite poulie en tr/min
ND : vitesse de la grande poulie en tr/min
ωd et ωD : vitesses en rad/s
d : diamètre d'enroulement petite poulie
D : diamètre d'enroulement grande poulie
Cd : couple sur la petite poulie en N.m
CD : couple sur la grande poulie en N.m b)

6. Cinématique.

b) Étude dynamique
Cette étude peut être généralisée aux autres courroies.
Données :
T : tension du brin tendu (en N)
t : tension du brin mou « t <T » (en N)
T0 : tension initiale de la courroie (en N)
f: coefficient de frottement entre poulie et courroie
P : puissance transmissible (en W)
V : vitesse (linéaire) de la courroie (en m/s)
m : masse de 1 m de courroie (kg/m)
θ= θd: arc d'enroulement sur la petite poulie (en rad)
Hypothèse : les forces de frottement entre poulie et courroie sont supposées uniformes sur toute la longueur de l'arc d'enroulement.
Rapport entre les tensions T et t
Cas 1 : effets de la force centrifuge sur la courroie négligés
Après une étude statique on obtient :

Cas 2, en tenant compte de la force centrifuge (F) sur la courroie


7. Efforts de tension.
Couples transmis

Tension t maximale admissible (Tmaxi)
Si T0 est la tension initiale (appliquée au moment de l'installation) lorsque la courroie tourne à vide (T ≈ t ≈ T0), en fonctionnement sous charge on a :
T = T0 + ζf(pour le brin tendu)
t = T0- ζF (pour le brin mou)
Après addition des deux : T0 = ½(T + t) .
T est maximale lorsque t est minimale (t = 0) : Tmaxi = 2T0
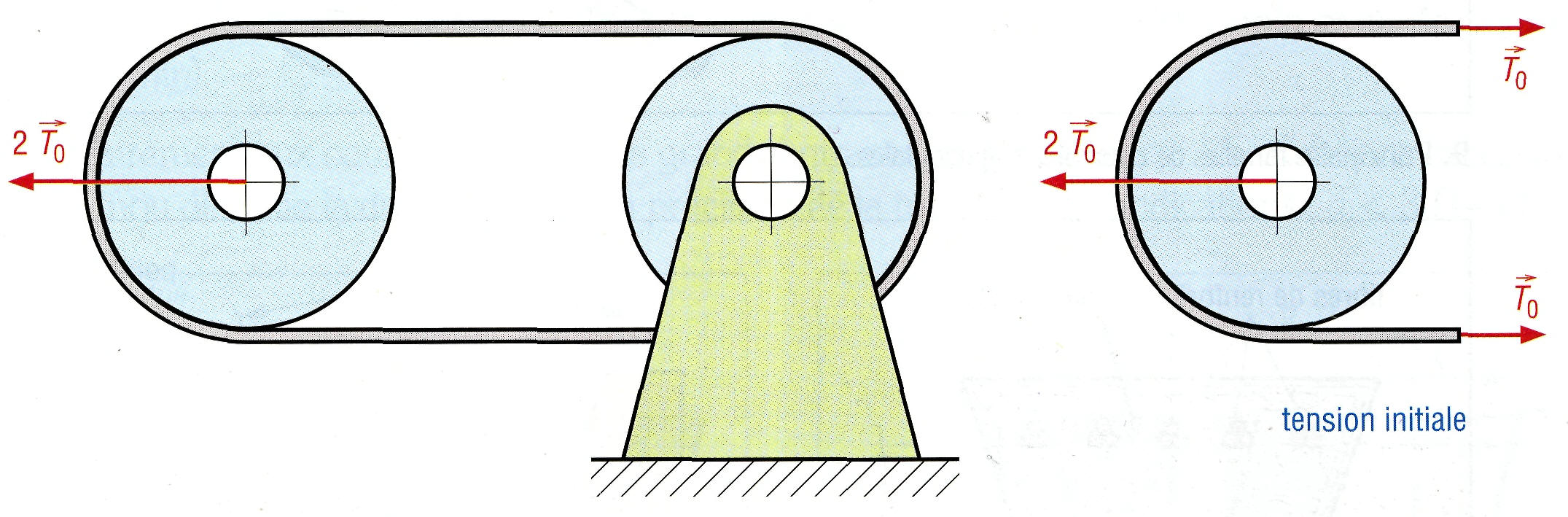
8. Tension initiale d'une courroie.
Puissances transmissibles
En fonctionnement normal : P = (T - t).V
Puissance maximale transmissible (cas ou Tmaxi = 2T0) :
P = (Tmaxi-tmini).V=(2T0-0).V=2T0.V
En pratique on pose : P = 2.KP.Kv.T0.V / Ks
P en watts
T0 en N
V en m/s
Kp : coefficient correcteur fonction du diamètre de la poulie
Kv : coefficient correcteur fonction de la vitesse (V) de la courroie
Ks : coefficient correcteur fonction des conditions de service (tableau 1. ci-après)
On peut poser Pb = 2.Kp.Kv.T0.V = puissance de base de la courroie avec la condition [P.Ks ≤ Pb].

2. Courroies trapézoïdales
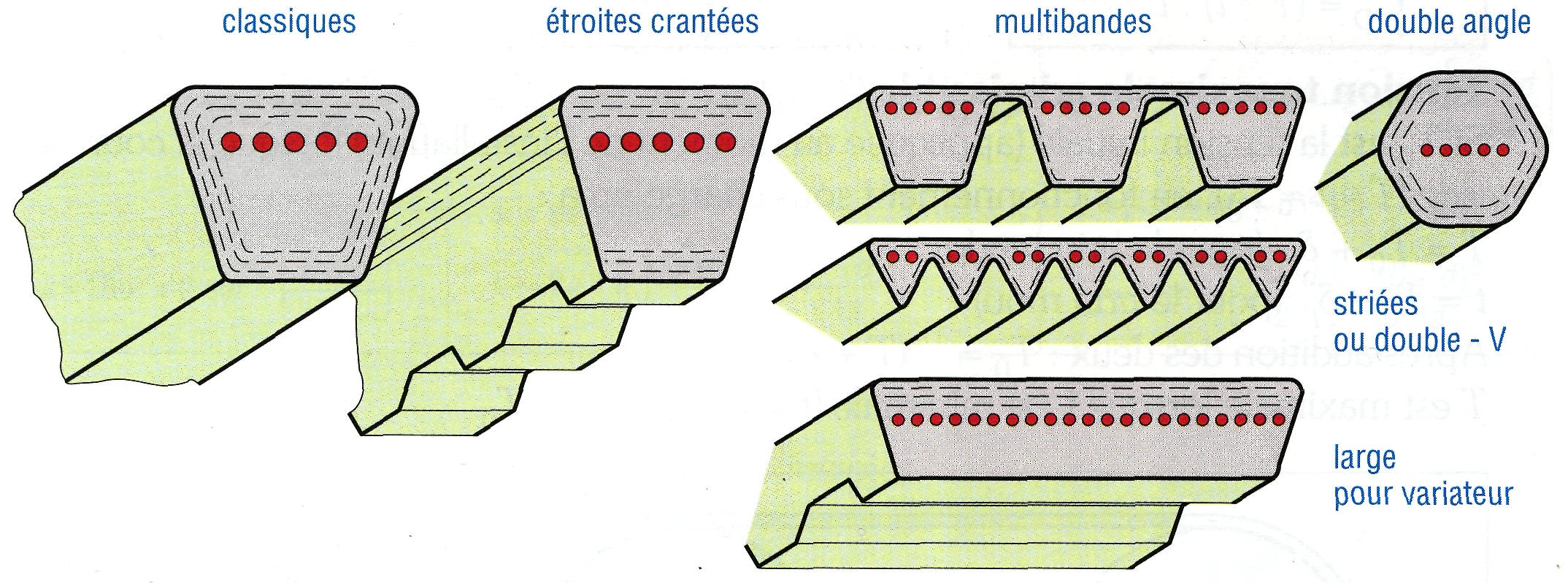
9. Principales familles de courroies trapézoïdales.

10. Efforts presseurs exercées par la gorge d'une poulie
sur une courroie trapézoïdale.

11. Exemples d'application des courroies trapézoïdales.
Les courroies trapézoïdales sont les plus utilisées ; à tension égale elles transmettent une puissance plus élevée que les courroies plates (conséquence de la forme en V augmentant la pression de contact et par là l'effort transmissible).
Si une puissance élevée doit être transmise on peut utiliser plusieurs courroies en parallèles sur la même poulie (avec 1, 2, 3..., 10 gorges).
Le montage nécessite un bon alignement des poulies et un réglage de l'entraxe pour le montage et le démontage.
Remarques:
- Pour obtenir de bons résultats et une bonne transmission, la courroie doit aller suffisamment vite (environ 20 m/s).
Les problèmes apparaissent au-dessus de 25 m/s et en dessous de 5 m/s (schématiquement 4 000 tr/min est une bonne vitesse ; des problèmes au-dessus de 5 000 tr/min et au-dessous de l000 tr/min).
- Contrairement aux courroies plates, les grands entraxes sont à éviter car les vibrations excessives du brin mou diminue la durée de vie et la précision de la transmission [indications : α < 3(D+d)].
 |
 |
| 12. Séries classiques et étroites. | 13. Montage sur une poulie
(β = 32°, 34°, 36°, 38°). |
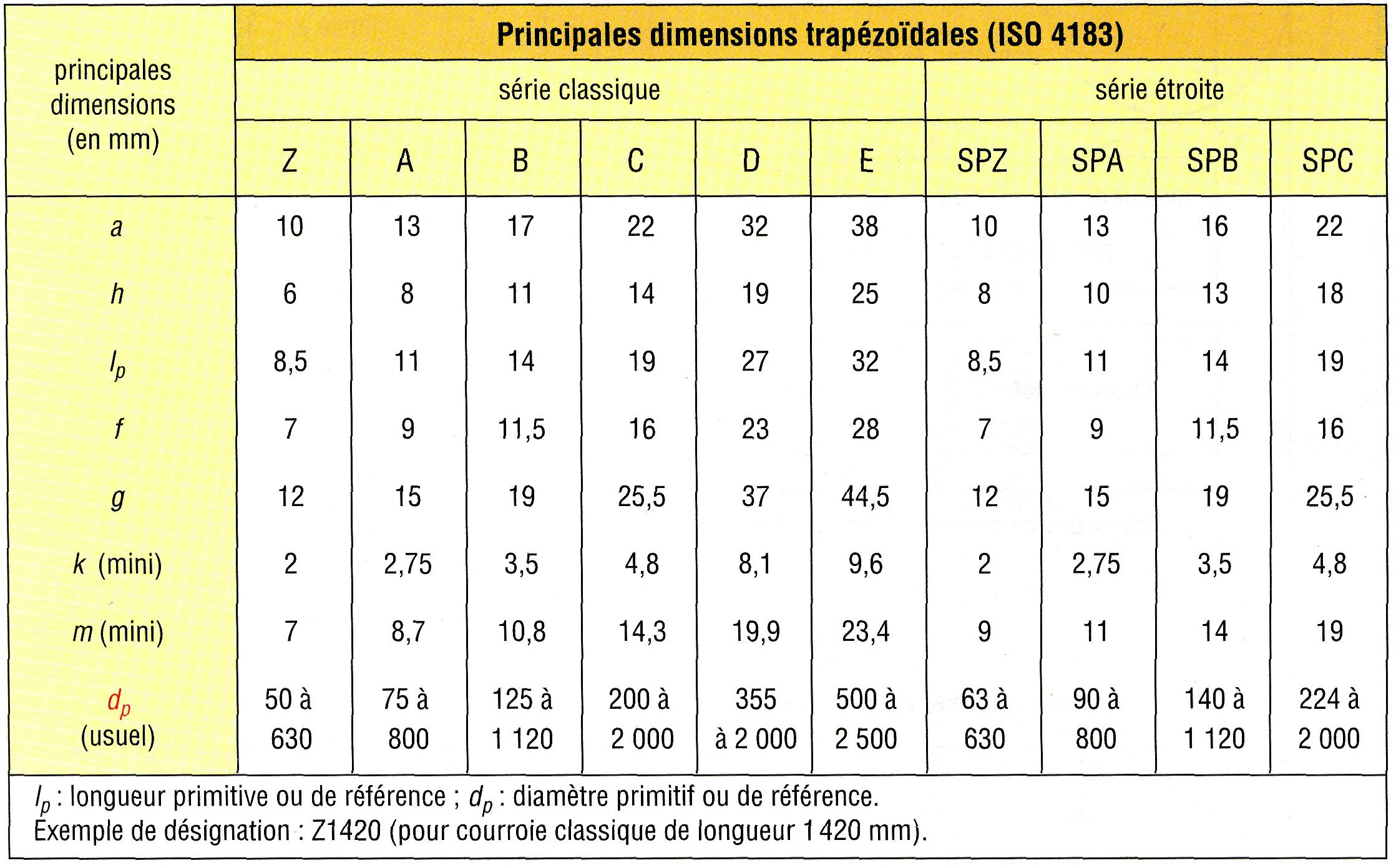
La série étroite (SPZ, SPA...) permet des transmissions plus compactes que la série classique (Z, A, B...) ; les courroies sont plus flexibles et les calculs identiques. Un crantage intérieur augmente la flexibilité et la capacité à dissiper la chaleur aux hautes vitesses.
Les courroies striées ont une action coinçante moins marquée et leur fonctionnement se rapproche plus de celui des courroies plates.
a) Étude générale
Elle est identique à celle des courroies plates sauf que d et D sont remplacés par dp et Dp , diamètres primitifs des poulies, et que β intervient.
Indication : 3 ≤ T/t ≤ 5 et le plus souvent T≈5t
b) Calcul des courroies trapézoïdales
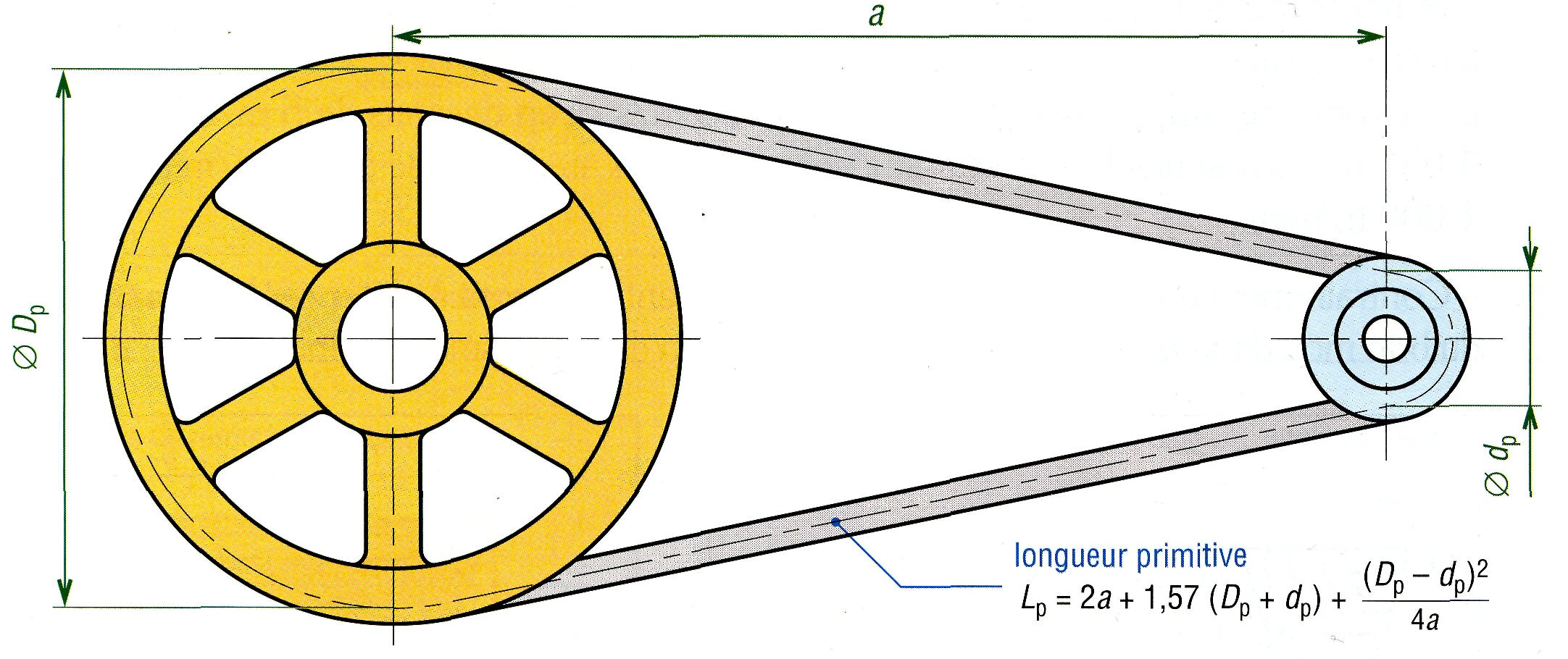
14. Ligne primitive d'une courroie trapézoïdale.

15. Principe de calcul des courroies trapézoïdales.
Le principe est résumé par l'organigramme de la figure 15.

16. Graphe 1 : gamme des puissances transmissibles par type de courroie.
Remarques :
- Plus le diamètre des poulies est grand, plus la durée de vie est grande. Les puissances de base (Pb) indiquées tableau 4, en tiennent compte et sont déterminées pour un angle d'enroulement de 180°. Le coefficient Kθ permet de faire les corrections pour des angles d'enroulement différents.

17. Graphe 2.
- Plus la longueur de la courroie est grande, plus la durée de vie est élevée (chaque tronçon de courroie travaillant moins) ; le coefficient KL permet de faire les corrections.

18. Graphe 3.
Données :
Nd : vitesse de la petite poulie (tr/min)
ND : vitesse de la grande poulie (tr/min)
dp : diamètre primitif de la petite poulie
Dp : diamètre primitif de la grande poulie
L : longueur primitive de la courroie
lp : largeur primitive de la section de la courroie
V : vitesse linéaire de la courroie (m/s)
P : puissance réelle à transmettre (W)
Ps : puissance de service ou puissance corrigée
Pb : puissance de base de la courroie
Pa puissance admissible par la courroie
KL : coefficient correcteur fonction de la longueur primitive Lp
Ks : coefficient correcteur lié aux conditions de service de la transmission
Kθ coefficient correcteur fonction de l'angle d'enroulement θ
θ= θd: angle d'enroulement sur la petite poulie





c) Exemple de calcul
Soit à déterminer les courroies transmettant une puissance de 10 kW entre un moteur électrique (1 500 tr/min) et une machine de production (600 tr/min) travaillant de 6 à 15 h/jour.
Résolution
On adopte un Ks de 1,3 pour l'installation.
Ps = P.Ks= 10.1,3 = 13 kW
Le graphe 1 (fig. 16) permet de sélectionner les courroies de type B.
Diamètres primitifs
dp = 140 mm est imposé pour la petite poulie.
Pour la grande poulie :

Vitesse linéaire de la courroie

Entraxe α
avec Dp/dp = 2,5 on prend a ≥ ½(Dp+dp)+dp = 385 mm = αmini
limite supérieure : α < 3(Dp + dp ) = 1 470 = αmaxi
Pour des raisons d'encombrement et compte tenu du tableau 3, on retient α = 437 mm
Longueur primitive courroie :
Lp = 2 x 437 + 1,57(350 + 140) + (350 - 140)2/(4.437) = 1 668 mm
Puissance de base de la courroie
(tableau 4, avec dp = 140 et V = 11 m/s) :
Pb = 4,16 kW (obtenue par interpolation entre 3,95 et 5,02)
Puissance admissible de la courroie choisie
Pa = Pb.KL.Kθ KL
KL ≈ 0,94 (graphe 3 avec Lp = 1668) ;
Kθ ≈ 0,93 (graphe 2 avec θ = 152,19°)
θ = 180° - 2 sin-1((Dp - dp)/2a)
=
180° - 2 sin-1((350 - 140)/2 x 437)) = 152,19°
Pa = 4, 16.0, 94.0, 93 = 3,64 kW
Nombre nécessaire de courroies : nc = 13/3,64 = 3,57 (soit 4 courroies)
3. Courroies crantées (ou synchrones)
On peut les considérer comme des courroies plates avec des dents. Elles fonctionnent par engrènement, sans glissement, comme le ferait une chaîne mais avec plus de souplesse.
Contrairement aux autres courroies, elles supportent bien les basses vitesses et exigent une tension initiale plus faible.
 |
 |
| 19. Exemple de
transmission par courroie crantée. |
20. Caractéristiques des courroies crantées. |


 |
 |
| 21. Graphe 4 : (gammes) puissances transmissibles des courroies crantées. | 22. Graphe 5 : puissance de base des courroies crantées. |
Calcul des courroies crantées
II est analogue à celui des autres courroies.
Rapport de transmission

Zd : nombre de dents de la petite poulie
ZD : nombre de dents de la grande poulie
Puissance de service : Ps = P.Ks (Ks par tableau 1)
Détermination du pas, ou du type de la courroie par l'intermédiaire du graphe 4 (à partir de Ps et Nd la vitesse de la petite poulie).
Vitesse linéaire V de la courroie : V = Nd.p.Zd/60
Remarque π.d =p.Zd = circonférence primitive de la petite poulie
Puissance de base (Pb) de la courroie choisie par l'intermédiaire du graphe 5 ; les Pb indiquées le sont pour une largeur de référence de 5 mm.
Choix de la largeur de la courroie sachant que Pb.Kb ≥ Ps
Kb coefficient correcteur fonction de la largeur des courroies (tableau ci-dessous)

Remarque : si l'on a moins de 6 dents en prise (Zpr < 6) sur la petite poulie, il faut utiliser le coefficient correcteur supplémentaire Kz (PbKb.Kz ≥ Ps)