Formules pratiques
Chaudière, Machines à Vapeur, 4e et 3e Classes 1954
ARITHMÉTIQUE DE LA MACHINE À VAPEUR
Problème de la chaudière
Comment trouver la surface de chauffe d'une chaudière horizontale à tubes de flamme (HRT)?
Du fait qu'un seul côté de la chaudière est exposé au feu, prenez la moitié du diamètre de la chaudière, en pouces, et multipliez par 3.1416.
Vous multipliez le produit ainsi obtenu par la longueur de la chaudière en pieds et vous divisez par 12. Vous avez ainsi la surface de chauffe de l'enveloppe.
Ensuite, vous multipliez le diamètre intérieur d'un tube ; en pouces, par 3.1416 et vous multipliez le produit ainsi obtenu par la longueur du tube en pieds, puis par le nombre de tubes, et vous divisez le produit par 12.
Dans le cas des chaudières autres que les HRT, on multiplie le diamètre extérieur ou externe.
La réponse vous donne la surface de chauffe des tubes en pieds carrés.
Ajoutez la surface de chauffe de l'enveloppe. La réponse vous donnera la surface de chauffe totale de la chaudière.
On peut plus commodément se servir du tableau suivant :
Problème:
II s'agit de trouver la surface de chauffe d'une chaudière ayant 5 pieds de diamètre, 15 pieds de longueur et contenant 82 tubes de 3 pouces.
L'installation de cette chaudière permet à la moitié de son enveloppe de venir en contact avec la flamme du foyer.
Du fait que la moitié seulement de l'enveloppe est soumise à l'action du feu, sa surface de chauffe sera:
1/2 x 5 x 3.1416 x 15 = 117.8 pieds carrés
On ne tient pas compte des extrémités de la chaudière, dont la surface de chauffe est négligeable.
La longueur totale des tubes est:
82 X1 5 = 1230 pieds
D'après le tableau ci-contre, il faut 1.373 pieds de longueur à un tube de 3" pour représenter 1 pied carré de surface de chauffe à l'intérieur.
Donc, la surface de chauffe de tous les tubes sera de:
1230 / 1.373 = 896 pieds carrés
La surface totale de chauffe de la chaudière en question sera de:
117.8 + 896 = 1,013.8 pieds carrés
Pression de marche et facteur de sécurité
On entend par facteur de sécurité d'une chaudière le rapport qui existe entre sa pression normale de fonctionnement et le point de rupture de ses parois (bursting pressure).
Connaissant la résistance du joint (effi-ciency of the joint), on obtient la pression à laquelle une chaudière peut être employée en toute sécurité au moyen de la formule suivante:
Pression de sécurité = 2 x Fm x T x Rj /F x D
Dans cette formule:
Fm = Force moléculaire (tensile strength) en livres par pouce carré.
Rj = Résistance du joint (Efficiency of the joint).
F = Facteur de sécurité
D = Diamètre de l'enveloppe du réservoir (drum).
T = Épaisseur de la paroi en pouces.
On trouve la résistance d'un joint (efficiency of the joint), au moyen de la formule suivante :
P - D / P
Dans cette formule:
P = l'espacement de centre en centre qui sépare chaque rivet, en pouces;
D = le diamètre du rivet.
La résistance des joints à recouvrement (lap joint) s'établit selon le module suivant:
joint à rangée de rivets unique, 56%; joint à deux rangées de rivets, 70%; à trois rangées 85-87%; à quatre rangées 94%.
Problème :
Quelle est la pression de marche de tout repos (safe working pressure) d'une chaudière dont l'enveloppe est faite d'une tôle ayant 5/8" d'épaisseur, avec une force moléculaire (tensile strength) de 60000.
Étant donné que la chaudière a 60" de diamètre et que ses joints sont faits à trois rangées de rivets, le facteur de sécurité étant 5 ?
En vous servant de la formule I, page 238, vous constaterez que:
La pression de marche (safe working pressure) égale:
(2 X 60000 X 0.625 X 0.87) / (5 X 60) = 217.5 lbs
0.625 en décimales = 5/8
0.87= résistance d'un joint à trois rangées de rivets.
CHEVAUX-VAPEUR (H.P.)
Un cheval-vapeur (H.P.) représente l'évaporation de 34.5 livres d'eau par heure à une température de 212° Fahrenheit, de manière que cette vapeur se transforme en vapeur sèche saturée à la même température.
On assume que 10 pieds carrés de surface de chauffe produisent nominalement UN cheval-vapeur.
Problème :
Quelle est la force en chevaux-vapeur d'une chaudière ayant 42" de diamètre et 18 pieds de longueur, ladite chaudière ayant 2 tubes-foyer de 12" chacun ?
Si l'on estime que la moitié de la circonférence de la chaudière constitue sa surface de chauffe, on trouvera ladite surface de chauffe par l'opération suivante:
0.5 X 42 X 3.1416 X 18 / 12 = 99 pieds carrés
0.5 en fractions décimales = 1/2
La surface de chauffe des tubes-foyer est de:
(12 x 3.1416 x 18 x 2) / 12 =113 pieds carrés
La surface de chauffe est donc: 99 + 113 = 212 pieds carrés.
Si l'on accorde 10 pieds carrés de surface de chauffe par cheval-vapeur, la force nominale de la chaudière en question sera de
212 / 10 = 21.2 H.P.
FACTEUR D'ÉVAPORATION
Le facteur d'évaporation est la proportion de B.T.U. requises pour évaporer une livre d'eau sous diverses températures d'alimentation et pressions de vapeur, par rapport au nombre de B.T.U. nécessaire pour évaporer une livre d'eau à 212°F en vapeur sèche saturée à la même température.
Sous ces conditions, il faut 970.4 B.T.U. pour évaporer une livre d'eau. On notera que ce chiffre correspond à la chaleur latente de la vapeur sous une pression atmosphérique normale de 14.7 lbs, absolue.
On obtient le facteur d'évaporation en soustrayant la température de l'eau d'alimentation de la chaleur totale de la vapeur telle que donnée dans les tables de vapeur, puis en divisant le produit par 970.4.
Problème:
Quel est le facteur d'évaporation d'une chaudière opérant à 120 lbs de pression absolue et dont l'eau d'alimentation accuse une température de 160°F ?
L'eau d'alimentation ayant une température de 160°, on trouve par la table de vapeur que ceci correspond à 127.9 B.T.U. par livre.
À 120 livres de pression absolue, la vapeur contient 1,191.4 B.T.U. par livre de chaleur totale. La chaleur accumulée dans la chaudière est donc de 1191.4 —127.9 = 1063.5 B.T.U. par livre de vapeur.
Maintenant, pour trouver le facteur d'évaporation, il suffit de diviser la chaleur accumulée par livre de vapeur dans la chaudière, par 970.4 (la chaleur requise pour produire une livre de vapeur dès et à 212°F), ce qui donne:
1063.5 / 970.4 = 1.097 — c'est le facteur d'évaporation
Si l'on voulait trouver combien de chevaux-vapeur cette chaudière développe, il faudrait connaître, en plus des données ci-dessus, ce que produit la chaudière en évaporation.
Et en admettant que son évaporation soit de 8,760 livres de vapeur à même une eau d'alimentation dont la température est de 160°, on trouverait le nombre de chevaux-vapeur développés au moyen de l'équation suivante:
8760 X 1.097 / 34.5= 278.5 H.P.
EFFICACITÉ OU RENDEMENT D'UNE CHAUDIÈRE
Le rendement d'une chaudière est le rapport de la quantité de chaleur utilisée à la quantité de chaleur produite par le combustible brûlé.
La formule pour trouver l'efficacité d'une chaudière est la suivante:
Problème I :
Supposons une chaudière de 250 H.P. qui produit la vapeur à 150 livres de pression absolue à même une eau d'alimentation de 200° et à raison de 10 livres de vapeur par livre de charbon utilisée.
En admettant que ce charbon donne 13000 B.T.U. par livre, il s'agit de trouver l'efficacité ou rendement de la chaudière.
La chaleur totale de la vapeur à 150 livres de pression absolue est de 1194.7 B.T.U. par livre.
La température de l'eau, au-dessus de 32°, est, à 200°, de 168 B.T.U. La chaleur accumulée de la chaudière se trouve donc de 1194.7 - 168 + 1026.7 B.T.U.
Du fait que l'évaporation est de 10 livres de vapeur par livre de charbon, un total de 10 x 1026.7, soit 10267 B.T.U. est absorbé par la chaudière par livre de charbon consumée.
Du fait que le charbon contient 13000 B.T.U. par livre, l'efficacité de la chaudière sera de:
10267 / 13000 soit 0.788, ou 78.8 pour cent.
Problème II:
Au cours d'une épreuve qui a duré 10 heures, une installation de chaudière à vapeur a consommé 5350 livres de charbon.
Du fait que ce charbon contenait 13,500 B.T.U. par livre et qu'au cours de la période du test 35120 livres de vapeur sèche saturée ont été produites à une pression de 150 livres par pouce carré au manomètre, avec une température de 210° pour l'eau d'alimentation, on veut savoir quelle est l'efficacité ou rendement de la chaudière.
La chaleur totale que contient la vapeur à 150 livres de pression au monomètre est de 1195 B.T.U. par livre.
La température de l'eau d'alimentation, au-dessus de 32° à 210°F. est de 178 B.T.U. La chaleur absorbée par la chaudière par livre de vapeur est donc :
1195 - 178 = 1017 B.T.U.
On a consommé un total de 5350 livres de charbon qui ont produit 35120 livres de vapeur.
La chaleur totale de la vapeur produite, divisée par la chaleur totale du combustible dépensé, donnera l'efficacité ou rendement, de la chaudière, des grilles et du foyer, soit:
(35120 x 1017) / (13500 X 5350) = 0.495 ou 49.5%
PROBLÈMES RELATIFS AU POMPAGE TÊTE D'EAU
La tête d'eau totale d'une pompe alimentaire est représentée par la vitesse de l'eau ajoutée à la friction et au poids total de la colonne d'eau.
On trouve la pression d'une colonne d'eau en multipliant sa hauteur en pieds par la constante .434. Cette constante est établie sur le fait qu'une colonne d'eau d'un pouce carré et haute d'un pied pèse .434 de livre.
Problème :
Trouver le nombre de chevaux-vapeur requis pour actionner une pompe, ordinaire à vapeur de manière qu'elle fournisse 200 gallons à la minute contre une tête d'eau de 250 pieds.
En admettant que la pompe ait une efficacité mécanique de 100%, elle exigerait:
200 x 8.3 x 25 / 33000 = 12.6 H.P.
mais vu qu'en pratique, l'efficacité mécanique n'atteint guère que 63%, l'énergie qui sera nécessaire pour faire fonctionner cette pompe sera de:
12.6 / 0.6 = 20 H.P.3
Pour trouver les dimensions de la pompe qui suffira à alimenter une chaudière, il importe de calculer combien de vapeur on aura besoin par heure.
On arrive à ce résultat en multipliant par 30 la puissance établie — en chevaux-vapeur (rated horse-power) — de la chaudière, puis en ajoutant de 15 à 20% comme facteur de sécurité.
La pompe doit être assez puissante pour alimenter la chaudière dans les conditions normales à une vitesse, disons, de 30 à 40 mouvements du piston par minute.
Connaissant la consommation en eau et le nombre de coups de piston par minute, il est facile ensuite de déterminer quelles devront être les dimensions du cylindre.
En admettant, par exemple, qu'on veuille trouver les dimensions du piston qui devra délivrer 4800 livres d'eau par heure, le nombre de coups de piston étant de 30 par minute, on effectuera les opérations suivantes :
II y a 62½ livres d'eau dans un pied cube d'eau, de sorte qu'en pieds cubes, l'alimentation en eau par minute sera:
4800 / (62.5 X 60) = 1.28 pied cube
Par conséquent, à chaque coup de piston de la pompe, il faudra déplacer:
1.28 pied cube / 30 ou 1.28 / (30 X 1728) = 73.73 pouces
— ce qui exige approximativement une course de 6 pouces pour le piston dans un cylindre ayant un diamètre de 4 pouces.
En effet, la capacité d'un cylindre de ces dimensions en pouces cubes, est:
4" X 3.1616 X 6" = 75.3984
PROBLÈMES RELATIFS AUX MACHINES À VAPEUR
RENDEMENT THERMIQUE
On entend par rendement thermique des machines à vapeur le rapport qui existe entre la chaleur utilisée par la machine et celle qui sert à produire la vapeur.
Problème :
Admettons qu'il faille trouver le rendement thermique de deux machines à vapeur.
La première consomme par heure 20 livres de vapeur par cheval-vapeur à 125 livres de pression par pouce carré (absolue), tandis que la deuxième consomme 19 livres de vapeur par heure par cheval-vapeur à 225 livres de pression absolue par pouce carré.
Toutes les deux ont un échappement à la pression atmosphérique et utilisent la vapeur saturée.
La chaleur utilisée par livre de vapeur à 125 livres de pression est 2545 / 20 = 127.3 B.T.U. pour la première de ces deux machines.
Elle est de 2545 / 19 = 134 B.T.U. pour la seconde. (Une heure/cheval-vapeur représente 2545 B.T.U.).
La chaleur du liquide est, dans les deux cas, 180 B.T.U., du fait que l'échappement se fait à la pression atmosphérique et donne à la vapeur de sortie une température de 212°.
La chaleur totale de la vapeur à 125 psi. est 1190.03 B.T.U.; à 225 psi. elle est de 1199.1 B.T.U.
Le rendement thermique de la machine opérant à 125 livres de pression sera donc:
127.3 / (1,190.3—180) = 0.126 = 12.6%
Celui de la machine opérant à 225 livres par pouce carré sera, à son tour de :
134 / (1199.1 - 180) = 0.131 = 13.1%
D'où l'on conclut que le rendement thermique de la machine opérant à 225 psi. ou livres par pouce carré de pression est plus haut de 0.5 pour cent que celui de la machine opérant à 125 livres de pression par pouce carré.
RENDEMENT MÉCANIQUE DES MACHINES À VAPEUR
On entend par rendement mécanique d'une machine à vapeur la force qu'elle développe réellement en regard de celle qu'on lui attribue.
En d'autres termes, c'est le pourcentage d'énergie mécanique produite dans le cylindre qui sert à accomplir un travail utile.
Problème:
Quel est le rendement mécanique d'une machine à vapeur qui donne 180 chevaux-vapeur au frein, alors qu'elle est censée en donner 200 ?
Rendement mécanique = 180 / 200 = 0.90 ou 90%
Pm = Pression de marche (Working pressure).
T = Épaisseur de la tôle d'acier.
Fm = Force moléculaire (Tensile Strength).
E = Pourcentage d'efficacité de l'acier dont les parois sont fabriquées.
R = Rayon.
F = Facteur de sécurité.
I
Pour trouver la pression de marche :
Pm = (Fm x T x E) / (R X F)
II
Pour trouver l'épaisseur que doit avoir la tôle d'acier d'une chaudière:
T = (R x F x Pm) / (Fm X E)
III
Pour trouver le module de force moléculaire (Tensile Strength) :
Fm = (Pm x E x RF) / (T X E)
IV
Pour trouver le pourcentage d'efficacité de l'acier employé:
E = (R x F x Pm) / (Fm X T)
V
Pour trouver le rayon:
R = (Fm X T X E) / (Pm X F)
VI
Pour trouver le facteur de sécurité :
(Fm x T x E) / (R X Pm)
Extraction manuelle de racine
Les carrés parfaits de 1 à 100 sont les carrés des 9 premiers nombres.
Nombres: 1 2 3 4 5 6 7 8 9
Carrés: 1 4 9 16 25 36 49 64 81
Règle
Pour extraire la racine carrée d'un nombre, on partage ce nombre en tranches de deux chiffres à partir de la droite.
On extrait d'abord la racine carrée de la dernière tranche à gauche, ce qui donne le chiffre des plus hautes unités de la racine et un premier reste ;
on abaisse à la droite de ce reste la tranche suivante du nombre, et on divise les dizaines du nombre ainsi formé par le double de la racine déjà trouvée ; ce qui donne, après essai, le deuxième chiffre de la racine et un deuxième reste;
on abaisse à la droite de ce reste la tranche suivante du nombre, et on opère sur le nombre ainsi formé comme sur le nombre précédent; ce qui donne le chiffre suivant de la racine ; et, ainsi de suite, on continue jusqu'à ce qu'on ait abaissé la dernière tranche du nombre.
Le dernier reste est le reste de la racine.
Racine carrée d'un nombre entier
Pour extraire à 0.1, à 0.01, à 0.001 près, la racine d'un nombre entier on extrait la racine du nombre entier, on place une virgule à la racine et on continue l'opération en abaissant deux zéros sur la droite des restes successifs de la racine jusqu'à ce qu'on ait à la racine le nombre des chiffres décimaux demandés.
Racine carrée d'un nombre décimal
Pour extraire la racine carrée d'un nombre décimal, on extrait d'abord la racine carrée de la partie entière du nombre, on place une virgule à la racine, puis on continue l'opération en abaissant à la droite des restes successifs, par tranche de deux, les chiffres décimaux du nombre, jusqu'à ce qu'on ait à la racine le nombre des chiffres décimaux demandés.
Racine carrée d'une fraction
Pour extraire la racine carrée d'une fraction, on extrait la racine carrée de chacun des termes de cette fraction.
Si possible convertir la fraction en décimales, et procéder ensuite comme ci-dessus.
Extraction abrégée de la racine carrée
On calcule d'abord par la méthode ordinaire la moitié plus un du nombre des chiffres de la racine entière ; puis on divise le reste par le double de la racine trouvée suivie d'autant de zéros qu'il reste de chiffres à obtenir.
Le quotient entier est le complément de la racine entière.
Exemple : Extraire la racine carrée de 189 225
Pour extraire manuellement la racine carrée d'un nombre "n" :
Partager votre feuille de travail en deux colonnes.
premiers. La valeur obtenue s'appelle "x". Écrire "x" en dessous de "n".
virgule à "v".
Exemple détaillé : Calculer la racine de 2
 |
 |
 |
 |
 |
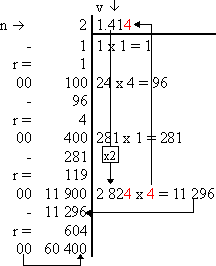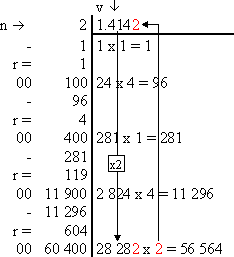Exemple non détaillé : Calcul de la racine de 54.321
La racine cubique de 1 881 365 963 625 = 12345
