Développement en traits parallèles

Les objets formés de lignes parallèles qui s'opposent les unes aux autres, ou qui présentent la même forme dans leur coupe en longueur, se développent facilement à l'aide de traits parallèles.

Développer la surface d'un solide, c'est étendre cette surface sur un plan, sans plis ni déchirures. La surface à développer est d'ailleurs considérée comme inextensible — autrement dit, elle n'accuse aucun changement dans sa superficie.

Nous venons de le voir, les surfaces cylindriques (prismes et cylindres), ainsi que les surfaces coniques (pyramides et cônes) sont développables, tandis que les surfaces sphériques ne le sont guère.

Le développement des surfaces nécessite le développement des lignes de contour; c'est pourquoi il est utile d'expliquer tout d'abord ce qu'on entend par développer et rectifier une ligne.

Développer une ligne brisée ou une ligne courbe, c'est appliquer ces lignes dans toute leur longueur soit sur une ligne droite, soit sur une autre courbe donnée. Le développement rectiligne, qu'on appelle aussi rectification, consiste à porter bout à bout, sur une droite unique, les parties successives d'une ligne brisée ou d'une ligne courbe.

Fig. 168.— Rectification d'une ligne brisée et d'une ligne courbe.

Ainsi, pour rectifier le contour ou périmètre du polygone que fait voir notre fig. 168, il suffit de porter consécutivement sur une droite indéfinie a . . .a les côtés AB, BC, CD, DE, EF et FA en ab, bc, cd, de, ef et fa.

De même, pour rectifier le contour de la pièce N, on partage ce contour, à l'aide du compas, en un certain nombre de parties sensiblement rectilignes; puis, sur une droite indéfinie m ... N, on reporte ces mêmes longueurs avec le compas. Dans le cas que fait voir notre fig. 168, on a partagé le contour en 15 parties, mais comme l'unité de mesure ne se trouve pas contenue un nombre exact de fois dans la courbe totale, on y a ajouté la partie restante 15¹.

Enfin, si l'on reporte les divisions 1 2, 2 3, etc., sur une autre courbe r ... S, on obtient une sorte de développement curviligne qui prend parfois le nom de transformée de la courbe.

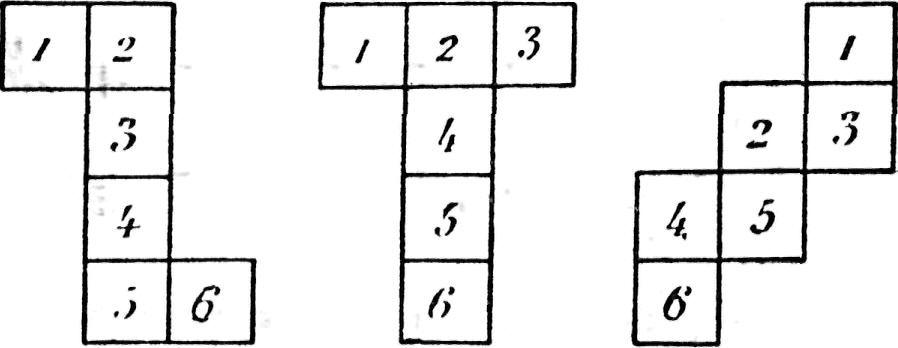
Fig. 169.— Trois autres développements du cube dont le procédé de développement le plus usité est donné en fig. 167.

La fig. 168 nous fait voir la manière de procéder pour développer sur une droite: l°le périmètre d'un hexagone ayant 1/2" de rayon, et 2° une circonférence ayant 7 lignes de rayon, enfin en 3° le développement de cette même circonférence sur un arc.

Nous avons vu tout à l'heure (fig. 167), comment on peut développer un cube en s'y prenant d'une certaine manière. La fig. 169, ci-contre, nous montre trois autres manières d'arriver au même résultat. Les six carrés formant le développement du cube peuvent en effet être contigus de plusieurs manières différentes.

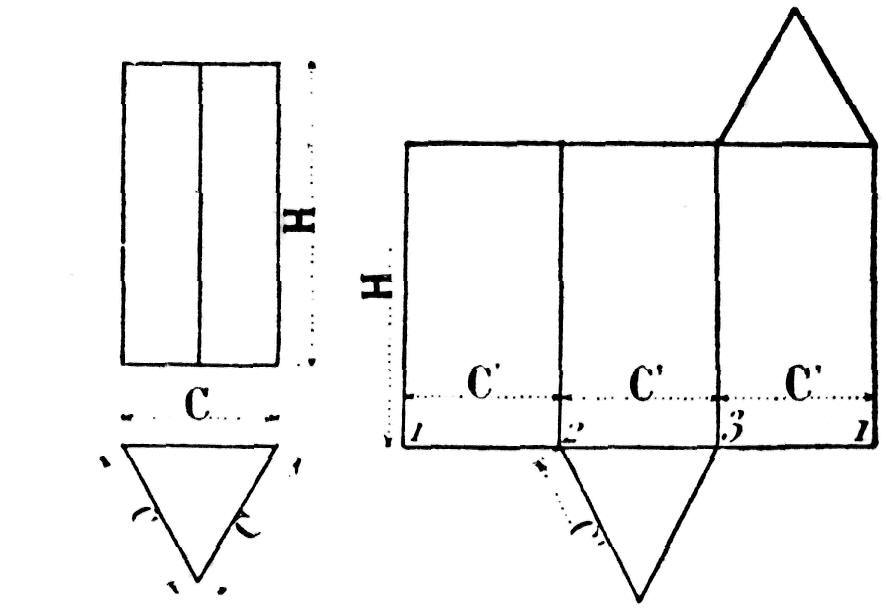
Fig. 170.— Développement d'un prisme régulier à base triangulaire.

Développement d'un prisme

Pour la construction de ce modèle en carton mince, représentant un prisme régulier à base triangulaire, (fig. 170), on donnera à l'arête C de la base 2", et à la hauteur du prisme H 5".

Le développement de ce solide se compose de trois rectangles égaux qui forment la surface latérale, et de deux triangles équilatéraux qui forment les bases.

Fig. 171.— Développement d'un prisme régulier à base carrée.

Cette fois (fig. 171) il s'agit d'un prisme régulier à base carrée. On pourra donner au côté C une dimension de 2" et à la hauteur de la construction 4". Le développement de la surface latérale se compose de quatre rectangles égaux. Sur le prolongement d'un des rectangles, on juxtapose les deux carrés de base.

Fig. 172.— Développement d'un prisme droit à base rectangulaire.

Voici maintenant (fig. 172) un prisme droit à base rectangulaire. On donnera au côté C 2", au côté D 1", et à la hauteur H 4".

Pour construire le prisme droit ayant pour base un losange que fait voir notre fig. 173, on donnera à la diagonale a, c 4" et  A la diagonale b, d 2", tandis que la hauteur du prisme sera de 3".

Le développement de la surface latérale du solide se compose de quatre rectangles ayant pour grande base la hauteur du prisme et pour petite base le côté du losange. On procédera comme suit pour construire ce losange sur le développement:

du centre A, décrivez l'arc BD',

du centre B, l'arc AD'C,

enfin du centre C (ou D'), décrivez l'arc C

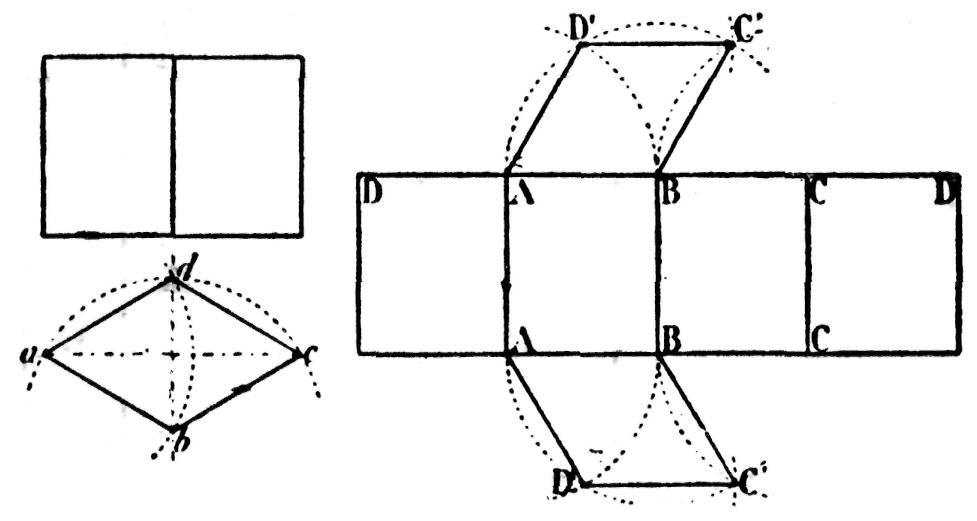
Fig. 173.— Construction d'un prisme droit ayant pour base un losange.

La fig. 174 nous montre l'application pratique des notions que nous venons de voir à la construction d'un prisme régulier à base hexagonale.

Fig. 174.— Développement d'un prisme hexagonal.

En (2), à gauche, on aperçoit  Les deux vues conventionnelles généralement fournies par le plan. Une ligne indéfinie AB est tracée à partir de la base de la vue de côté à angle droit de son axe vertical. Sur cette ligne, on porte six points également espacés correspondant chacun à la largeur de chacune des faces verticales du prisme.

La distance ainsi développée est égale au périmètre de l'hexagone. De chacun des points ainsi développés, on élève des perpendiculaires d'une hauteur égale à celle du prisme que montre la vue de face. Ceci est facilement obtenu en projetant la ligne CD, du sommet de l'élévation, parallèlement à la ligne AB. Chacune de ces perpendiculaires est numérotée 1, 2, 3, etc., pour correspondre aux chiffres inscrits sur la vue de dessus.

Les perpendiculaires élevées de AB à CD représentent les éléments du prisme. Le dessus et la base du prisme sont développés en reliant leurs contours respectifs à l'une quelconque des faces de n'importe quel des éléments. La technique que nous venons d'exposer s'applique au développement du prisme régulier à base pentagonale que fait voir notre fig. 175, ainsi qu'au prisme droit à base irrégulière, que montre la fig. 176.

Fig. 175.— Développement d'un prisme régulier à base pentagonale.

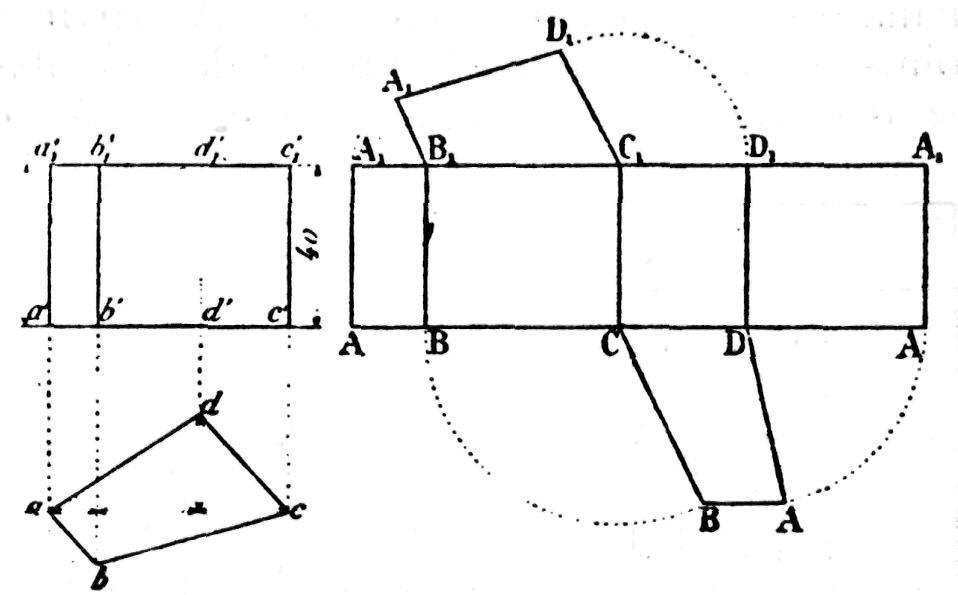
Fig. 176.— Développement d'un prisme droit à base irrégulière.

Coude hexagonal

Appliquons maintenant à un travail pratique ce qui vient d'être dit du prisme hexagonal. Il s'agit de développer un coude hexagonal coupé à 45° et dont les deux pièces servent à former un angle à 90°.

On commence par dessiner les vues de côté et de dessus (fig. 177), puis on projette une ligne horizontale AB, de longueur indéfinie, à partir de la base de la vue de côté.

A l'aide du compas à pointes sèches, on reporte la largeur des côtés sur cette ligne horizontale et, à partir des points ainsi repérés, on élève des perpendiculaires de longueur indéfinie.

A partir des points d'intersection de la vue de dessus, abaissez des verticales jusqu'à l'angle de 45° qui apparaît sur la vue de face. Des points ainsi repérés sur l'angle de la vue de face, projetez des lignes horizontales qui viendront recouper les perpendiculaires élevées tout à l'heure sur la ligne AB. Rejoignez ces points d'intersection par des droites qui vous donneront la forme du sommet de l'une des moitiés du coude. Une seule moitié étant ainsi développée, il n'est pas nécessaire de recommencer le même travail pour la seconde qui lui est absolument semblable.

Fig. 177.— Développement d'un coude hexagonal à 90°.

Cylindre droit

Un cylindre circulaire droit (right cylinder) offre des parois latérales perpendiculaires au plan de sa base. La largeur du patron du cylindre que fait voir la fig. 178 est la même sur toute la longueur du cylindre; de même, la longueur du patron, c'est-à-dire du développement de ce cylindre, est égale à la circonférence du cylindre à sa base.

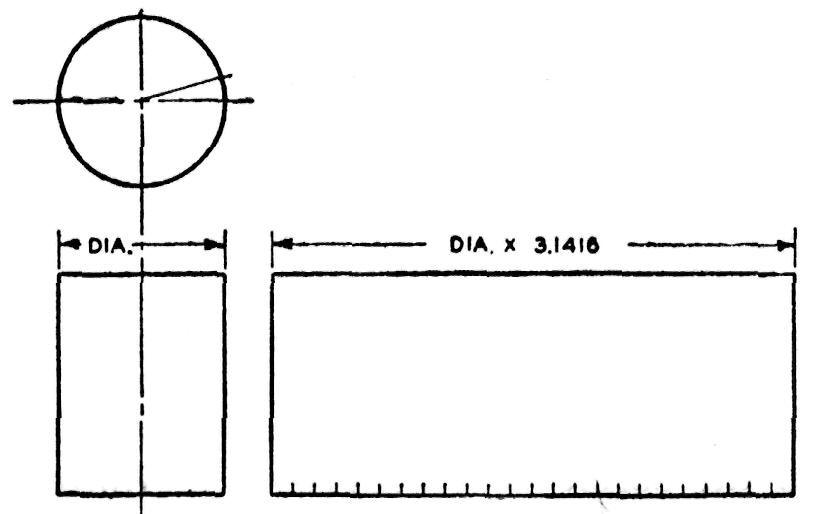
Fig. 178.— Développement d'un cylindre droit.

La circonférence d'un cylindre est toujours proportionnelle à son diamètre (3.1416 à 1).

Ainsi, un cylindre ayant 3" de diamètre aura une circonférence de

3 x 3.1416 = 9.4248

— et l'on choisira, sur la réglette à mesurer, la fraction de pouce qui se rapproche de plus de cette décimale.

On peut en outre obtenir comme suit la longueur que présentera le patron: décrivez un petit angle sur le cercle, lequel angle est contenu un nombre égal de fois dans la circonférence. Plus cet angle sera petit, plus près de la vraie circonférence se trouvera la longueur du patron.

Réglez l'écartement des pointes sèches du compas à la distance indiquée entre les points où les côtés de l'angle recoupent le cercle et reportez cette distance autant de fois sur la ligne de développement.

La précision de la longueur du patron sera vérifiée en en prenant la mesure et en comparant cette mesure avec la longueur calculée de la circonférence du cercle soit 3.1416 x le diamètre.

Cylindre tronqué

En admettant que l'on veuille obtenir le patron d'un cylindre tronqué à un certain angle (fig. 179), on dessinera les vues de côté et de dessus, et l'on projettera ensuite une ligne horizontale AB, de longueur indéfinie, à partir du bas de la vue de côté.

Puis, on divisera la vue de dessus en un nombre égal d'angles. On règle alors l'écartement des pointes du compas à la distance qui sépare les points où les côtés de l'angle recoupent le cercle et l'on reporte cette distance sur la ligne AB autant de fois qu'existent d'angles dans la vue de dessus. De chacun des points ainsi repérés sur la ligne AB on élève des verticales de longueur indéfinie.

Fig. 179.— Développement d'un cylindre tronqué.

Abaissez ensuite des verticales de la vue de dessus vers la vue de côté de manière à rejoindre l'angle formant le sommet de cette dernière. Des points ainsi repérés, projetez des lignes horizontales qui viendront recouper les verticales de longueur indéfinie élevées de la ligne AB en 1, 2, 3, 4, etc. En vous servant d'un pistolet, reliez les points de rencontre à l'aide d'une ligne légèrement courbe et vous obtiendrez le patron de votre cylindre.

Si, maintenant, vous voulez obtenir la forme que présentera la surface CD dans une vue auxiliaire, tracez la ligne d'axe EF à angle droit de CD, puis perpendiculairement à EF. Tracez la ligne d'axe GH parallèlement à CD. Sur GH tracez un demi-profil de la vue de dessus et sur cette demi-circonférence, reportez des divisions identiques à celles de la vue de dessus. Projetez alors des lignes parallèles à GH qui recouperont les lignes correspondantes de CD afin de repérer les points qui, dans la vue auxiliaire, vous donneront l'ellipse.

Si votre développement est bien exécuté, le patron, une fois assemblé, devrait présenter une surface angulaire qui s'appliquera exactement contre une surface plane sans laisser de «jour». N'oubliez pas, pour faire un patron de ce genre, de laisser suffisamment de carton pour que les joints chevauchent, ce qui permettra de les coller et de donner à votre patron une forme stable.

Les développements en parallèle de cylindres droits ne sont pas tous d'une facilité relative aussi apparente. Prenons, par exemple le cas d'un coude cylindrique à 90°, formé de trois sections, et dont notre fig. 180 fait voir la perspective.

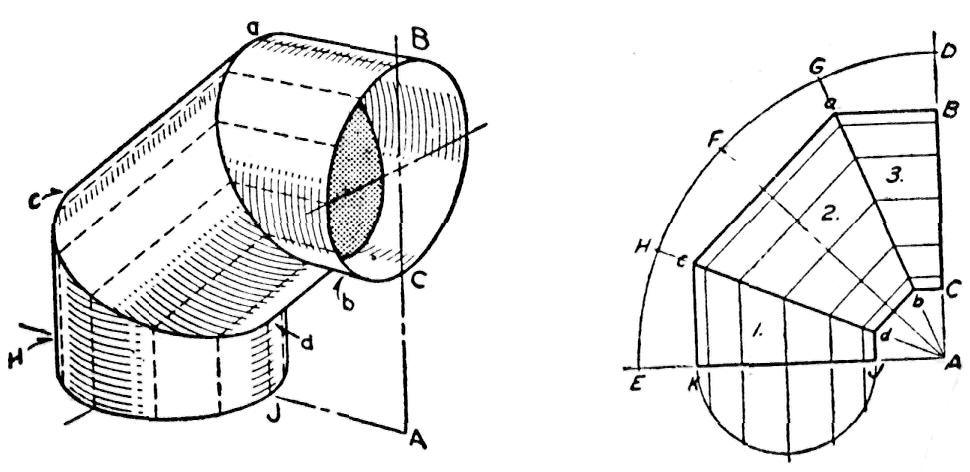
Fig. 180.— Perspective et vue de côté d'un coude cylindrique en trois sections.

Notez d'abord que les trois parties formant ce coude sont des portions de  Cylindre. Vous aurez recours au développement en parallèle dont nous avons parlé jusqu'à présent au sujet des cylindres droits, mais en y ajoutant certaines précautions.

Commencez par dessiner la vue de côté dont la fig. 180 donne le détail. Du point A construisez un angle droit. Mesurez la hauteur du coude le long de AD. Mesurez le diamètre du coude de B à C. Décrivez l'arc DE en prenant A comme centre à une distance convenable.

Maintenant, divisez l'angle EAD en quatre angles égaux en traçant les lignes FA, HA et GA. Des points B et C tirez des lignes horizontales qui viendront recouper la ligne de rayon GA. Repérez les points K et J à la même distance de A que sont B et C. De K et J   Tracez des verticales qui viendront recouper la ligne HA à c et d. Reliez les points a et c et les points b et d afin de compléter la vue de côté du coude.

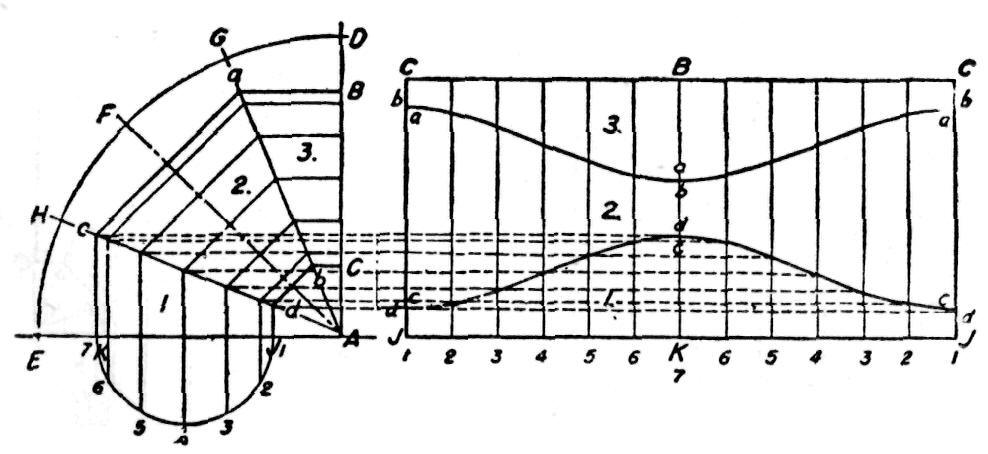
Fig.181.— Développement d'un coude cylindrique en trois sections.

Si, enfin, vous voulez faire le développement de ce coude, (fig. 181) voici comment vous allez procéder:

Le diamètre KJ de la demi-circonférence est le diamètre du cylindre formant ce coude.

On divise la demi-circonférence en six parties égales.

La longueur du développement JJ est la circonférence étendue d'un cercle ayant KJ pour diamètre.

La hauteur du développement JC est la somme de Jd, ca bc.

On obtient le contour inférieur du patron au moyen du développement parallèle. Le contour de la partie supérieure peut être reporté du contour inférieur au moyen du compas, mais, dans la pratique on l'obtient en se servant du premier comme gabarit.