Angles en perspective isométrique

Un objet possède rarement des faces parallèles au plan de projection en projection isométrique, de sorte qu'en général, les angles sur ces faces ne sont pas projetés en vraie grandeur sur les perspectives isométriques.

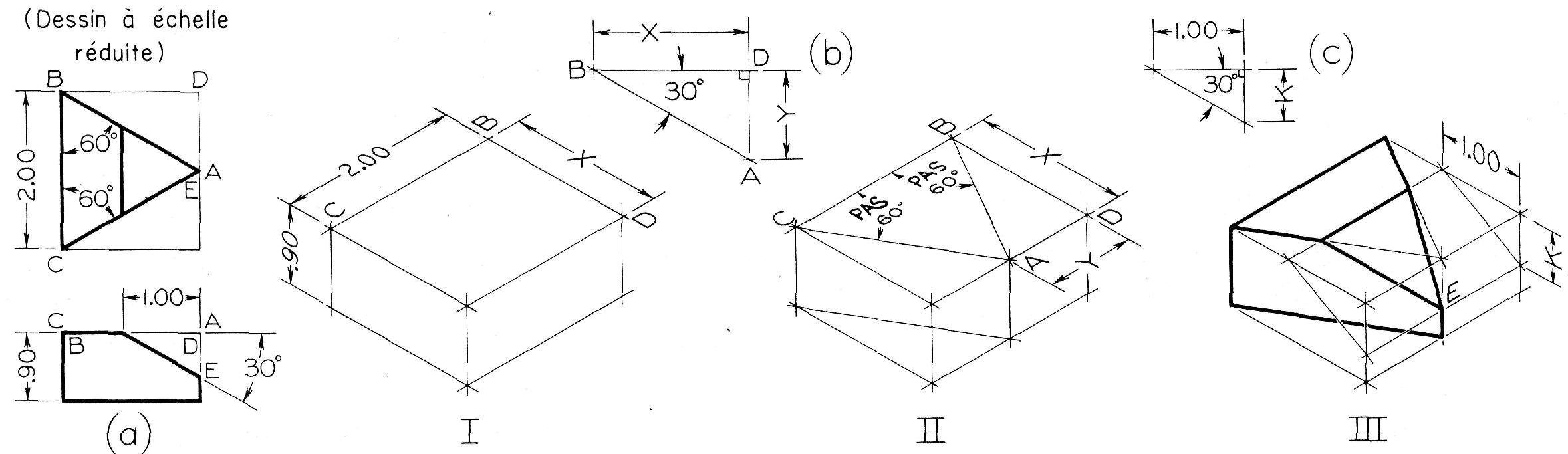
Ainsi, la perspective isométrique d'un cube ne comporte aucun angle droit. De même, à la figure 16.17.a, les angles aux sommets B et C de la vue de dessus ne seront pas de 60° en perspective, comme l'illustre la figure 16.17.1.

Figure 16.17
Angles en perspective isométrique

Par conséquent, on ne peut pas utiliser de rapporteur pour établir un angle en perspective isométrique. I1 existe, dans le marché, des rapporteurs spéciaux conçus pour les dessins en perspective isométrique. Il faut convertir les mesures angulaires en mesures linéaires le long des lignes isométriques.

A la figure 16.17.1, on peut tracer la boîte capable à partir des dimensions données en (a), excepté le côté X.

On le détermine graphiquement en construisant le triangle rectangle ABD à partir de l'hypoténuse AB et de l'angle de 30°. Cette construction fournit aussi la distance Y qui est utilisée, à l'étape II, pour localiser le point A.

À l'étape III, on complète la perspective en déterminant le point E à l'aide de la distance verticale K, laquelle est évaluée graphiquement en (c).

Les constructions graphiques (b) et (c) à la figure 16.17, destinées à déterminer les longueurs inconnues, peuvent aussi être effectuées directement sur le dessin en perspective (étapes I ou III de la figure 16.18). Naturellement, ces constructions deviennent superflues si, à la figure 16.18, la cote X est donnée au lieu de l'angle de 30°.

Figure 16.18
Angles en perspective isométrique