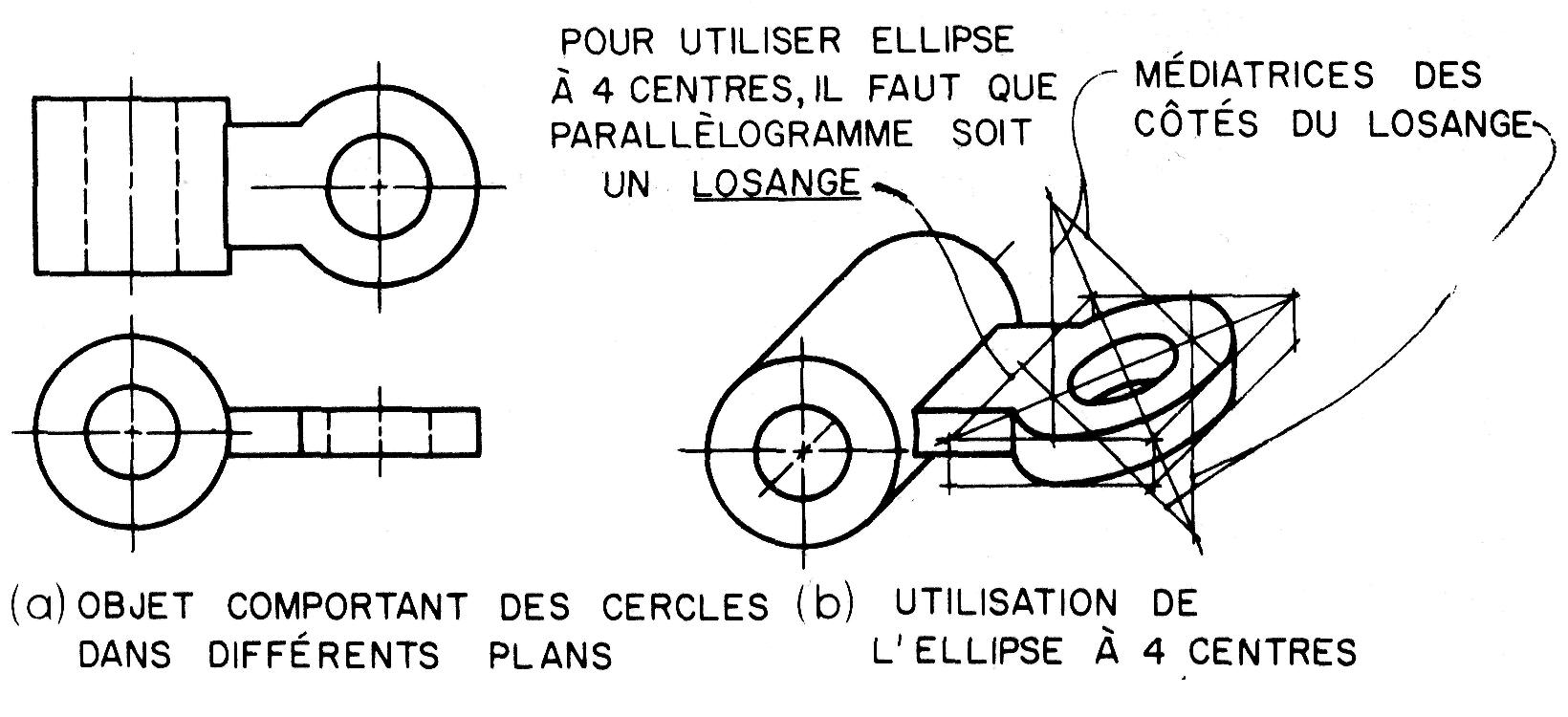
Ellipse à quatre centres

Il n'est pas toujours possible de placer toutes les caractéristiques circulaires d'un objet parallèles au plan de projection et, du même fait, de les représenter en vraie forme. L'objet illustré à la figure 17.14. a en fournit un exemple: les deux contours circulaires ne se trouvent pas sur des plans parallèles.

Figure 17.14
Tracé des ellipses

Dans la perspective oblique représentée en (b), la méthode des quatre centres (figure 16.24 section Problèmes sur les perspectives obliques) a été utilisée pour tracer les ellipses horizontales.

Cette méthode n'est applicable qu'aux perspectives cavalières, c'est-à-dire lorsque les fuyantes sont dessinées en vraie longueur. A la figure 17.14.b, l'angle de fuite (l'angle que font les fuyantes avec l'horizontale) est de 30°, de sorte qu'on peut utiliser une équerre à 30° et le té pour trouver les quatre centres.

Si l'angle de fuite est différent de 30°, il est préférable d'appliquer une autre méthode à quatre centres, basée sur les axes conjugués de l'ellipse (figure 17.15).

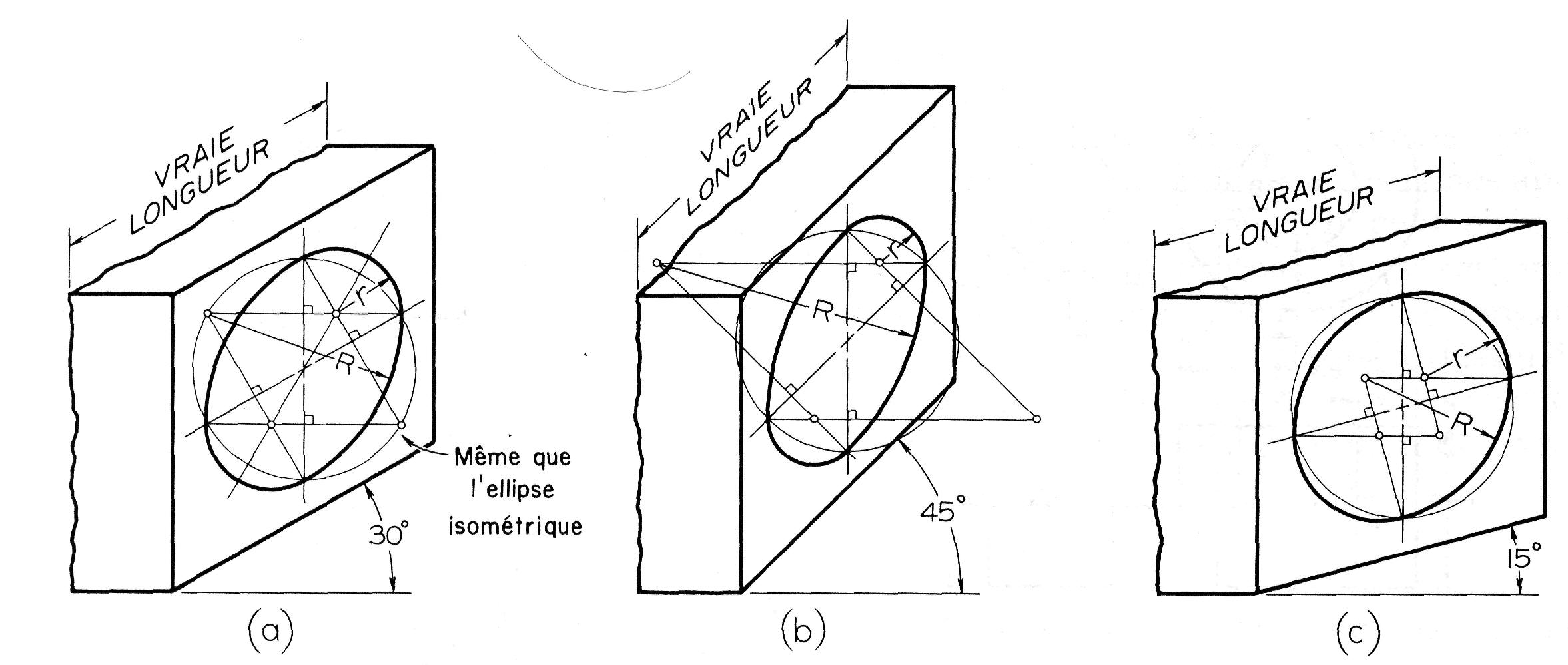
Figure 17.15
Ellipse à quatre centres — Méthode du cercle

Cette méthode est la même que celle illustrée à la figure 16.29 section perspectives isométriques dans Projection Axonométrique.

En premier lieu, on dessine les deux axes de l'ellipse. Ensuite, en traçant un cercle dont le rayon est égal au vrai rayon du trou, on obtient quatre points d'intersection sur les deux axes.

Comme l'illustre la figure 17.15, les autres perpendiculaires, dessinées à partir de ces points, se coupent en quatre points qui sont les centres à partir desquels les arcs de cercle seront tracés pour représenter l'ellipse.

Il faut se rappeler que l'ellipse à quatre centres n'est inscrite que dans un losange, son utilisation ne s'applique pas à toutes les perspectives obliques, mais seulement aux perspectives cavalières.