Rotation des cercles

Comme les figures 4.50.a à 4.50.c à la section Construction d'une ellipse dans Tracés géométriques l'illustrent, un cercle apparaît comme une ellipse quand il est vu obliquement. Dans ce cas, la pièce de monnaie est tournée par les doigts.

La construction géométrique de cette rotation est représentée à la figure 9.12.a.

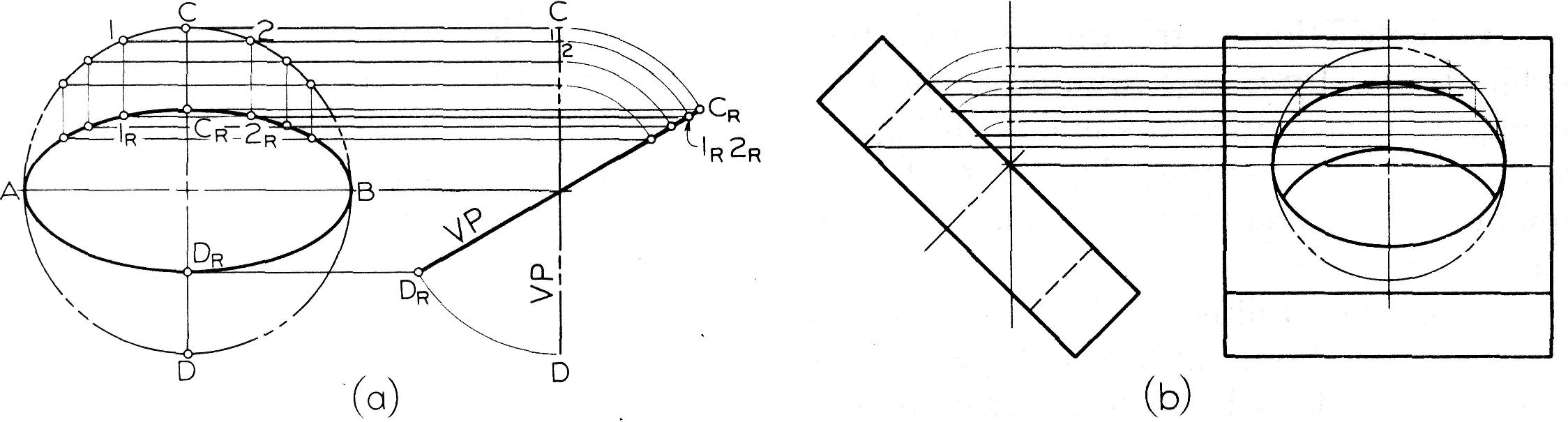
Figure 9.12
Rotation d'un cercle

Le cercle est en vraie grandeur, ABCD, dans la vue de face et en profil, CD, dans la vue de droite. Dans cette vue, CD est tourné d'un angle arbitraire jusqu'à Cr-Dr.

Pour obtenir différents points de l'ellipse, tracez une série de lignes horizontales qui traversent le cercle dans la vue de face.

Chaque horizontale coupe le cercle en deux points, 1 et 2 par exemple.

Projetez ces deux points sur CD de la vue de profil et faites-les tourner jusqu'à 1R2R, comme l'illustre la figure.

Projetez ce point sur la vue de face pour obtenir les points 1R et 2R de l'ellipse.

Déterminez autant de points qu'il en faut pour permettre la construction d'une courbe régulière.

La figure 9.12.b illustre une application de ce principe dans la représentation d'un grand trou vu obliquement.