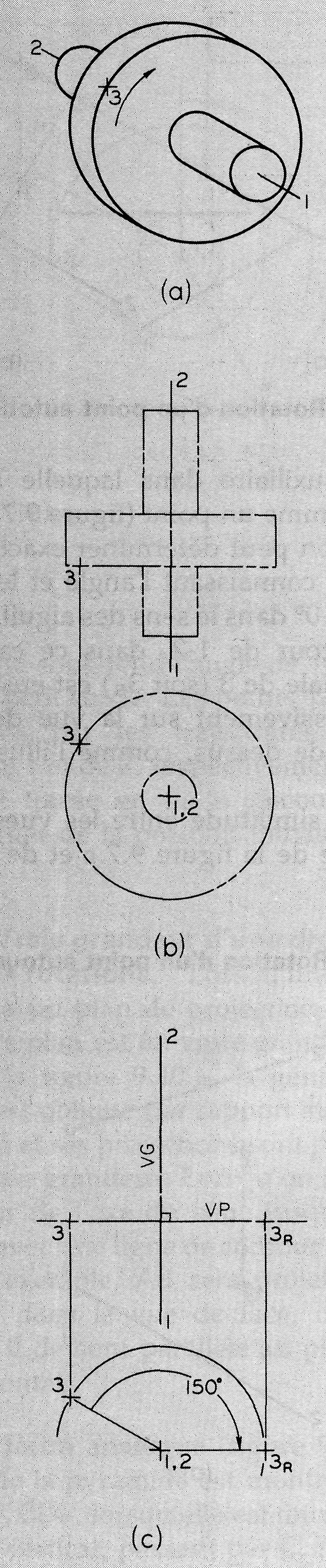
Figure 9.6
Rotation d'un point autour d'un axe normal
Rotation d'un point
Rotation d'un point — Axe normal à un des plans de projection principaux
La rotation d'un point autour d'un axe est un problème rencontré fréquemment lors de la conception de systèmes comportant des poulies, des engrenages, des manivelles, de la timonerie, etc.
Par exemple, lorsque le disque, représenté à la figure 9.6.a, tourne autour de l'arbre dont l'axe est 1-2, le point 3 se déplace le long d'un cercle perpendiculaire à 1-2.

Figure 9.6
Rotation d'un point autour d'un axe normal
Cette relation est clairement illustrée en (b), où deux vues du système sont représentées.
Les deux vues choisies sont les vues de face et de dessus, où l'axe de rotation 1-2 apparaît respectivement comme un point et comme sa vraie grandeur. Il en résulte deux propriétés fondamentales:
dans la vue où l'axe apparaît comme un point (vue de face dans ce cas-ci) la trajectoire est un vrai cercle et,
dans la vue où l'axe apparaît comme sa vraie grandeur (vue de dessus dans ce cas-ci), la trajectoire est une droite perpendiculaire à l'axe.
Ces deux propriétés existent toutes les fois qu'on est en présence de vues donnant ces mêmes caractéristiques de l'axe, en particulier lorsque l'axe est normal au plan horizontal ou au plan de profil.
Dans le cas général où l'axe a une direction quelconque (sections Axe incliné et Axe oblique), on doit déterminer d'abord les vues auxiliaires qui donnent lesdites caractéristiques.
La figure 9.6.c illustre la rotation du point 3, autour de l'axe 1-2, d'un angle de 150° dans le sens des aiguilles d'une montre.
Il est important de noter que le sens de la rotation est défini à partir du
sens de l'axe de rotation. Ainsi, dans l'exemple précédent, on peut aussi dire
que le point 3 tourne dans le sens contraire des aiguilles d'une montre autour
de l'axe 2-1.
Rotation d'un point — Axe incliné
A la figure 9.7.a, le point 3 doit tourner autour de l'axe incliné 1-2.
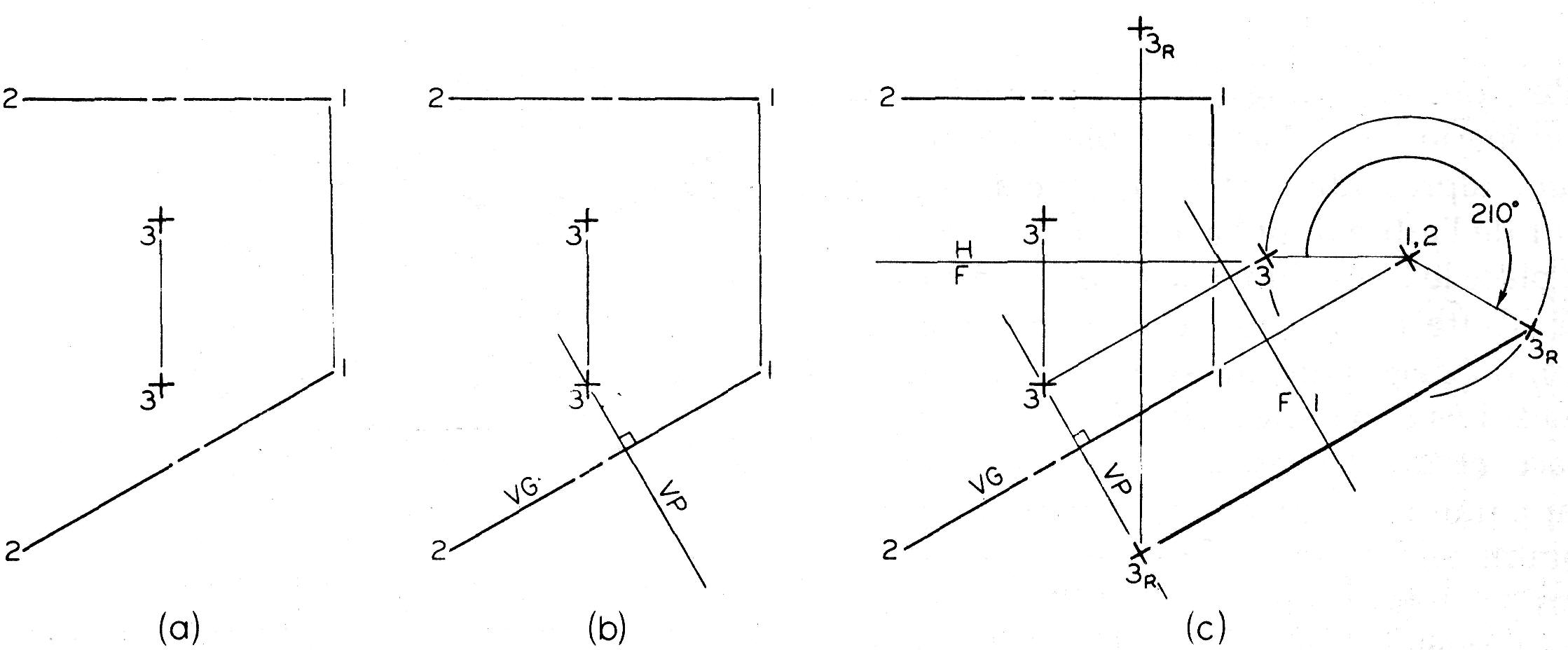
Figure 9.7
Rotation d'un point autour d'un axe incliné
Par définition, une droite est dite inclinée quand elle est parallèle à un seul des trois plans de projection principaux (section Surfaces et Arêtes inclinées dans Dessin à vues multiples).
Dans cet exemple, 1-2 est parallèle uniquement au plan frontal et, conséquemment, sa projection dans la vue de face est en vraie grandeur. De ce fait, la trajectoire de 3 dans la vue de face apparaît comme une droite perpendiculaire à 1-2 (figure 9.7.b).
Pour obtenir la vraie forme de la trajectoire circulaire de 3, il faut établir une vue auxiliaire dans laquelle l'axe 1-2 apparaît comme un point (figure 9.7.c).
Dans cette vue, on peut déterminer exactement la rotation en connaissant l'angle et le sens de rotation (210° dans le sens des aiguilles d'une montre autour de 1-2, dans ce cas-ci). La position finale de 3 (soit 3r) est ensuite projetée successivement sur la vue de face et sur la vue de dessus, comme l'illustre la figure.
Notez la similitude entre les vues de face et auxiliaire de la figure 9.7.c et de la figure 9.6.C.
Rotation d'un point — Axe oblique
Le point 3 de la figure 9.8.a doit tourner autour de l'axe oblique 1-2.

Figure 9.8
Rotation d'un point autour d'un axe oblique
Par définition, une droite est dite oblique quand elle n'est parallèle à aucun des trois plans de projection principaux (section Surfaces et Arêtes obliques dans Dessin à vues multiples).
L'axe 1-2 n'apparaît donc ni comme un point, ni en vraie grandeur dans aucune des vues principales. Pour obtenir ces deux caractéristiques nécessaires, il faut construire deux vues auxiliaires successives (figure 9.8.b).
La rotation requise du point 3 est alors déterminée dans la deuxième vue auxiliaire et, ensuite, projetée successivement sur les autres vues.
Notez qu'on obtiendrait les mêmes résultats si l'on choisissait des vues
auxiliaires adjacentes à la vue de dessus, à la place de la vue de face. Le
choix est simplement guidé par l'espace disponible sur la feuille de dessin.
