Arêtes parallèles

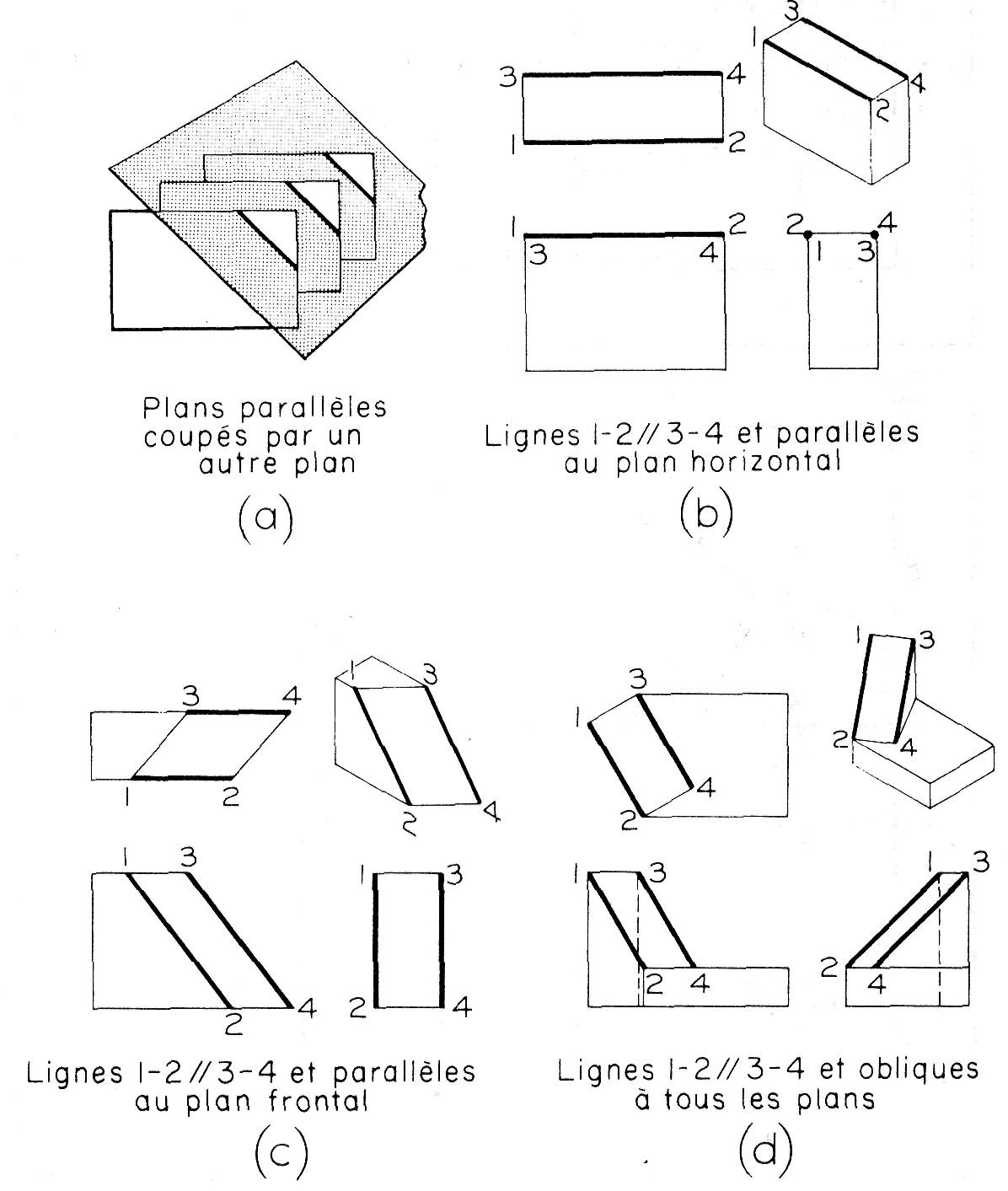
Les lignes parallèles dans l'espace sont projetées en des lignes parallèles sur toutes les vues. Les arêtes parallèles sont produites par l'intersection de plusieurs plans parallèles avec un plan quelconque (figure 6.27.a).

Figure 6.27
Droites parallèles

Les autres dessins de la figure 6.27 illustrent quelques exemples d'arêtes parallèles, du cas le plus simple (b) au cas le plus général (d).

A la figure 6.28.a, il faut établir les trois vues de l'objet donné, quand celui-ci est coupé par un plan (oblique) passant par les points A, B et C.

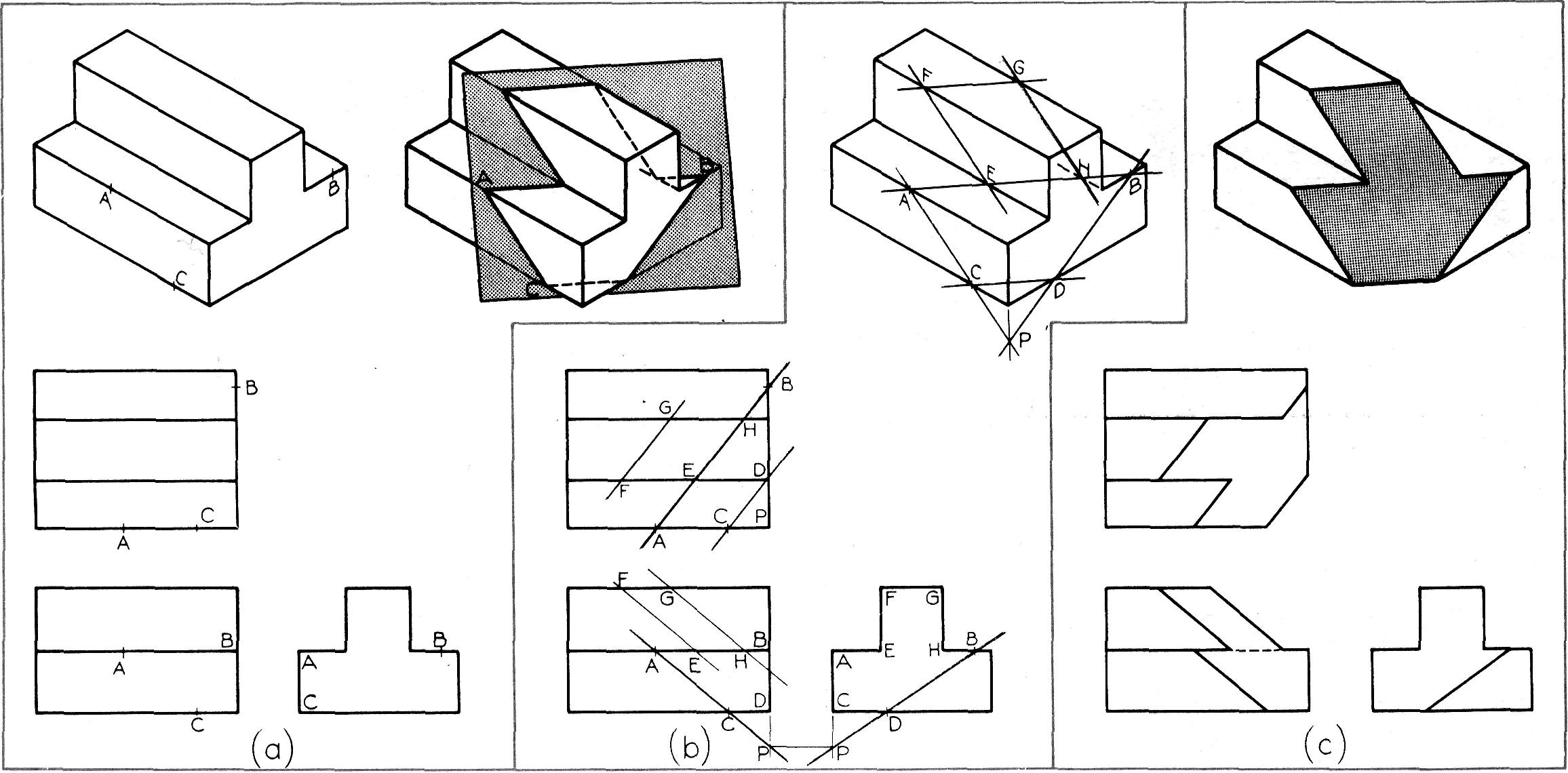
Figure 6.28
Surface oblique

Comme l'illustre la figure 6.28.b, le plan coupe, d'une part, les trois faces frontales de l'objet suivant trois lignes parallèles, AC, F E et G H et, d'autre part, les trois faces horizontales suivant trois autres lignes parallèles, FG, AB et DC.

Ainsi, dans la vue de dessus, on trace DC parallèle à AB.

Ensuite, dans la vue de face, on trace des parallèles à AC à partir de E et de H, qui sont déduits de leurs points correspondants dans la vue de dessus.

Ces parallèles déterminent F et G. Comme vérification, le point d'intersection P des prolongements de AC et de BD, dans les vues de face et de droite, doit se trouver sur la même ligne de rappel, puisque AC et BD se coupent réellement dans l'espace.