Le cube de référence

Si les plans de projections sont placés parallèlement aux faces principales de la pièce, ils forment un parallélépipède rectangulaire appelé cube de référence (voir la figure 6.3.a).

Figure 6.3
Le cube de référence

L'observateur regarde toujours la pièce de l'extérieur du cube. Comme le cube possède six faces, on obtient les six vues usuelles de la pièce.

L'objectif du dessin technique étant de placer les vues d'un objet tridimensionnel sur une feuille de papier, il faut déplier les faces du cube de façon à les rabattre toutes sur un même plan (figure 6.3.b).

Toutes les faces sont attachées à la face de front (plan frontal) à l'exception de la face arrière qui est attachée à la face de gauche.

Les lignes d'intersection entre les faces sont appelées charnières. Chaque face se rabat vers l'extérieur autour de chaque charnière jusqu'à ce qu'elle soit sur le même plan que celui de la face de front, qui est gardée fixe.

La figure 6.4 illustre la position des six faces du cube de référence, une fois déplié. primordial d'identifier soigneusement chacune des faces et les vues correspondantes par rapport à leurs positions originelles sur le cube, il importe de répéter mentalement ce rabattement, jusqu'à ce que le principe soit bien compris.

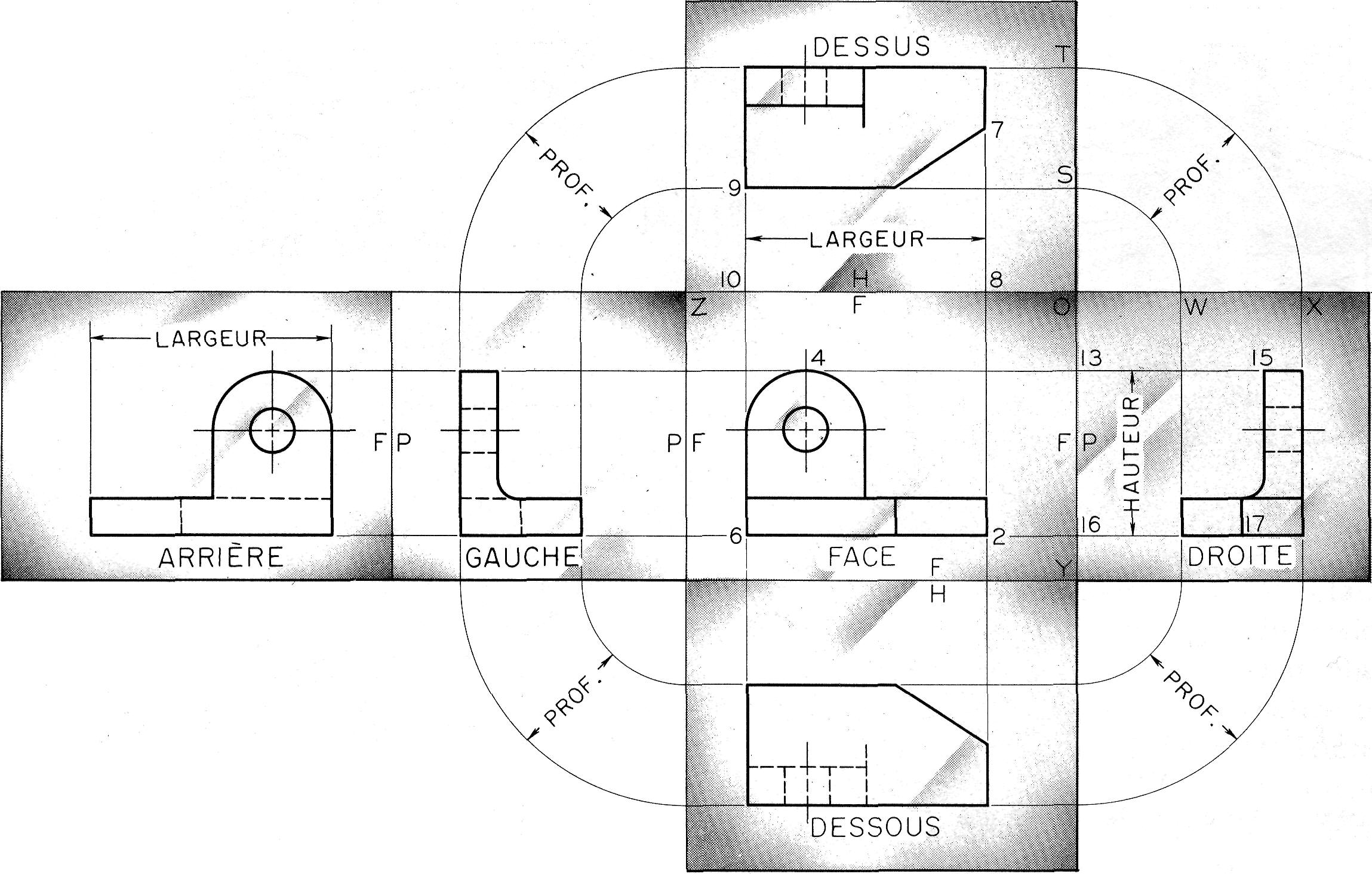
Figure 6.4
Le cube de référence déployé

A la figure 6.3.b, les lignes 7-8 et 9-10 sont respectivement les projections orthogonales des lignes 1 -2 et 5-6.

Quand la face de dessus est rabattue à la position verticale, 7-8 et 9-10 deviennent verticales et sont, par conséquent, les prolongements des lignes 8-2 et 10-6 (figure 6.4).

Ceci explique pourquoi la vue de dessus se trouve directement au-dessus de la vue de face et pourquoi elles ont la même largeur. Les droites 7-2 et 9-6 sont appelées lignes de rappel, tout comme les autres droites 4-15, 6-17, etc. (figure 6.4).

En appliquant le même raisonnement aux autres vues, on parvient à établir la relation qui existe entre les vues (figure 6.4):

les vues de dessus, de face et de dessous ont la même largeur et elles sont alignées verticalement;

les vues d'arrière, de gauche, de face et de droite ont la même hauteur et elles sont alignées horizontalement.

A la figure 6.3.b, on remarque que OS et OW sont égaux et que OT et OX sont aussi égaux.

Ces lignes sont illustrées dans la position dépliée à la figure 6.4. Ainsi, la distance entre la vue de dessus et la charnière ZO est la même que celle entre la vue de droite et la charnière OT, de plus, ces deux vues ont la même profondeur.

Ainsi, les vues de dessus, de droite, de dessous et de gauche sont à la même distance de leurs charnières respectives et elles ont la même profondeur.

On note enfin que les contours des six vues sont symétriques deux à deux, par exemple, le contour de la vue d'arrière est symétrique à celui de la vue de face.

Il est primordial d'identifier soigneusement chacune des faces et les vues correspondantes par rapport à leurs positions originelles sur le cube, il importe de répéter mentalement ce rabattement, jusqu'à ce que le principe soit bien compris.

A la figure 6.3.b, les lignes 7-8 et 9-10 sont respectivement les projections orthogonales des lignes 1 -2 et 5-6.

Quand la face de dessus est rabattue à la position verticale, 7-8 et 9-10 deviennent verticales et sont, par conséquent, les prolongements des lignes 8-2 et 10-6 (figure 6.4). Ceci explique pourquoi la vue de dessus se trouve directement au-dessus de la vue de face et pourquoi elles ont la même largeur.

Les droites 7-2 et 9-6 sont appelées lignes de rappel, tout comme les autres droites 4-15, 6-17, etc. (figure 6.4).

En appliquant le même raisonnement aux autres vues, on parvient à établir la relation qui existe entre les vues (figure 6.4):

les vues de dessus, de face et de dessous ont la même largeur et elles sont alignées verticalement; les vues d'arrière, de gauche, de face et de droite ont la même hauteur et elles sont alignées horizontalement.

A la figure 6.3.b, on remarque que OS et OW sont égaux et que OT et OX sont aussi égaux.

Ces lignes sont illustrées dans la position dépliée à la figure 6.4. Ainsi, la distance entre la vue de dessus et la charnière ZO est la même que celle entre la vue de droite et la charnière OT, de plus, ces deux vues ont la même profondeur.

Ainsi, les vues de dessus, de droite, de dessous et de gauche sont à la même distance de leurs charnières respectives et elles ont la même profondeur.

On note enfin que les contours des six vues sont symétriques deux à deux, par exemple, le contour de la vue d'arrière est symétrique à celui de la vue de face.