Intersections et tangences des surfaces

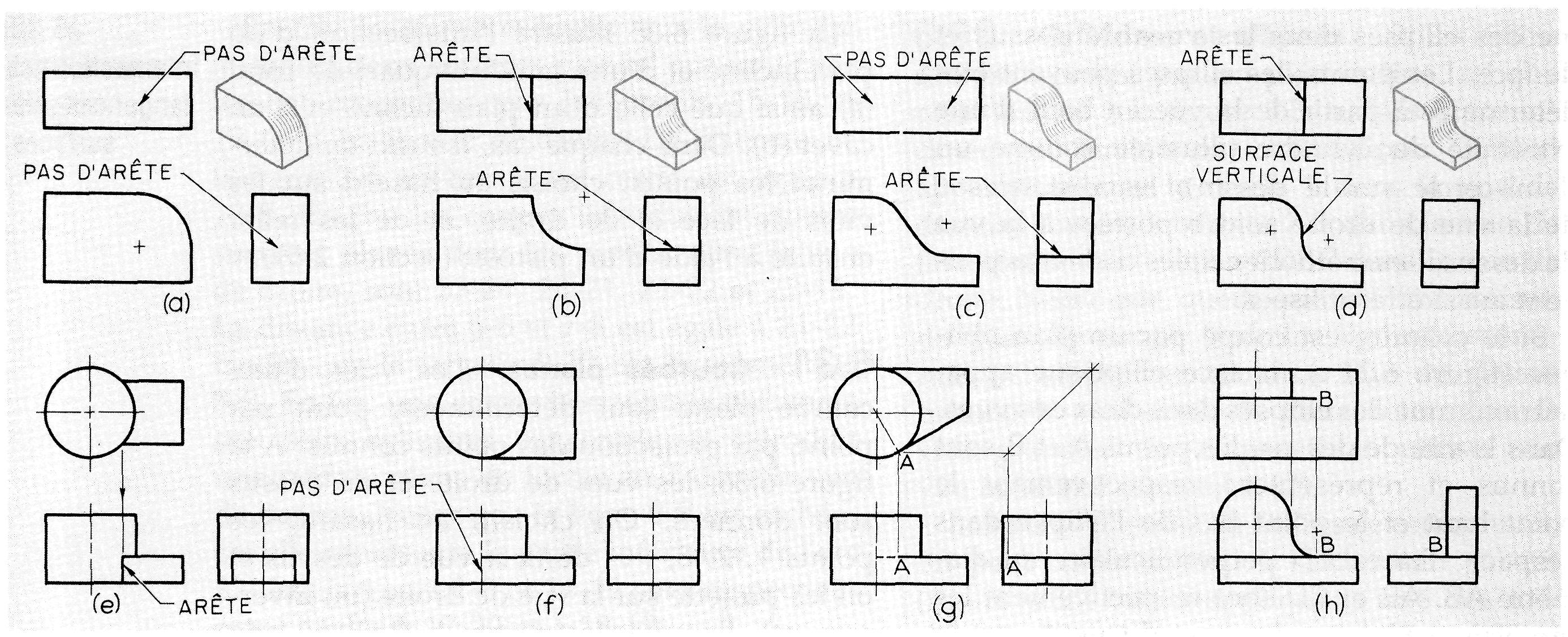
Quand une surface courbe est tangente à une surface plane (figure 6.37.a), on ne peut pas représenter le lieu de tangence par une ligne.

Figure 6.37
Intersections et tangences.

Par contre, quand une surface courbe coupe une surface plane (figure 6.37.b), il existe une arête bien définie.

Si les surfaces sont disposées comme celles à la figure 6.37.C, il n'y a qu'une seule arête dans la vue de droite. A la figure 6.37.d, l'arête dans la vue de dessus représente le contour apparent de la surface verticale. Les figures 6.37.e à 6.37.h fournissent d'autres exemples des intersections et des tangences possibles entre deux surfaces.

Différentes intersections entre deux cylindres sont illustrées à la figure 6.38.

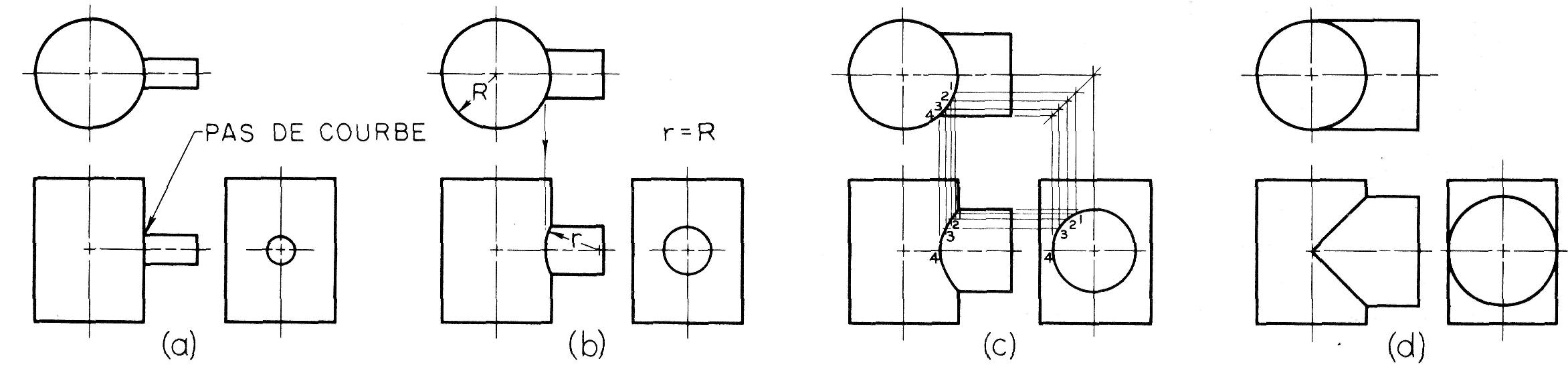
Figure 6.38
Intersections de cylindres.

En (a), l'intersection est tellement petite qu'il n'est pas nécessaire de tracer une vraie courbe, une ligne droite suffit.

En (b), l'intersection est un peu plus grande mais elle ne justifie pas encore la construction d'une courbe réelle. Dans ce cas, on trace symboliquement un arc de cercle dont le rayon r est égal au rayon R du grand cylindre.

En (c), on trace la courbe réelle d'intersection en projetant un nombre suffisant de points choisis dans les vues de dessus et de droite.

En (d), les deux cylindres ont le même diamètre et leurs intersections sont deux demi-ellipses qui apparaissent comme deux droites dans la vue de face.

Si les cylindres sont des trous, leurs intersections sont semblables à celles représentées à la figure 6.38.

A la figure 6.39.a, un prisme mince rencontre un cylindre.

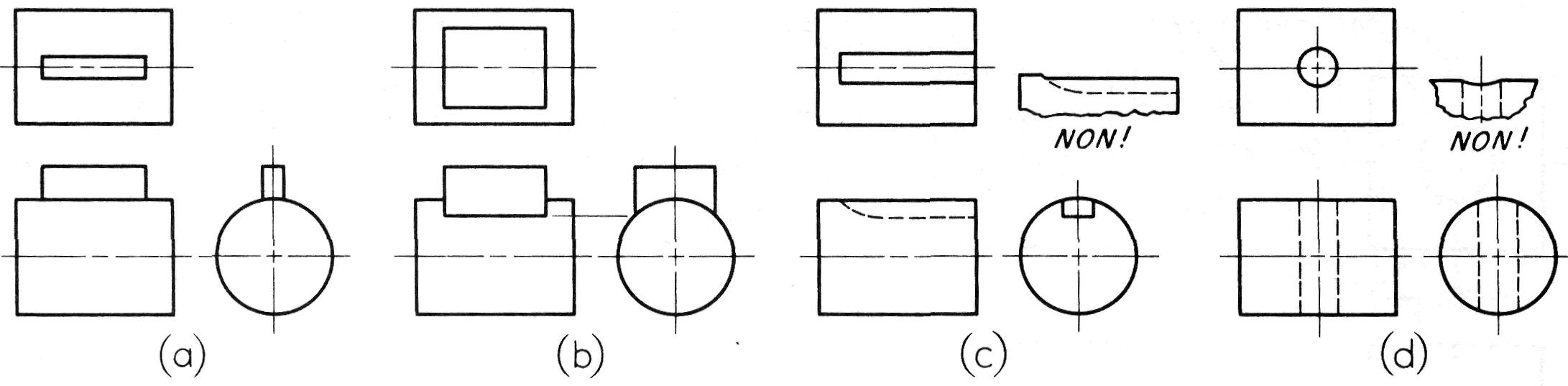
Figure 6.39
Intersections

La courbe d'intersection est négligeable de sorte que l'on n'en tient pas compte, ce qui n'est pas le cas de la situation illustrée en (b). De la même façon, il n'est pas nécessaire de tracer la vraie courbe d'intersection d'une rainure de clavetage (c) ou d'un petit trou (d).