Les nombres en informatique

Je n'ai jamais été très fort en math (ni dans les autres matières), et je me perds parfois avec les nombres dès que je dois les traiter dans le monde informatique. C'est pourquoi je me suis dit qu'il serait peut-être pratique de constituer une petite synthèse permettant de s'y retrouver un peu entre bits, octets, mots, surtout quand on doit s'attaquer à des conversions entre les différents types. Si j'ai fini par comprendre comment tout cela fonctionnait, je pense que vous aussi ne devriez pas avoir trop de difficulté pour y parvenir.

Codage des nombres en informatique

Dans le monde informatique, qui au niveau processeur ne sait reconnaitre que des valeurs logiques de type tout ou rien (0 ou 1), il est fréquent de travailler avec des nombres, catégorisés selon leur grandeur. Ainsi, on peut travailler avec un nombre qui ne peut prendre que deux valeurs comme le bit, tout comme on peut travailler avec des nombres qui peuvent prendre 256 valeurs différentes comme l'octet (byte en anglais, à ne pas confondre avec bit), ou encore avec des nombre de valeurs encore plus grandes. D'un point de vue machine, tous les nombres sont décrits par un nombre plus ou moins important de bits, car il n'y a pas moyen de faire autrement. Plus un nombre a une valeur élevée, et plus le nombre de bits nécessaires pour le "faire tenir" peut être important.

La catégorisation d'un nombre est simple : si on peut le faire tenir dans un petit "casier" (par exemple casier de type Octet), on se contente de ce type de casier, qui ne prend pas trop de place. S'il ne peut pas y tenir, on le met dans un casier plus grand (par exemple casier de type Word), qui prend certes plus de place mais qui devient nécessaire. Bien sûr, un nombre de faible valeur (par exemple 34) peut aussi bien tenir dans un petit casier (byte, dans lequel on peut ranger des nombres dont la valeur maximale est 255) que dans un grand casier (word, dans lequel on peut ranger des nombres dont la valeur maximale est 65535).

Élément binaire soliste : le bit

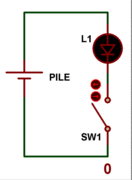
Comme déjà dit, l'élément binaire de base appelé bit peut prendre deux valeur, soit 0 soit 1. C'est une chose assez facile à assimiler, car comme le montrent les schémas suivants, on peut avec un seul fil, une pile, une ampoule et un interrupteur, transmettre visuellement l'information binaire 0 (ampoule L1 éteinte) ou l'information binaire 1 (ampoule L1 allumée) grâce à l'interrupteur SW1. 

 

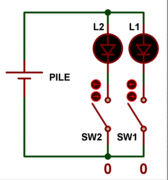
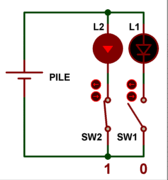
Premier élément binaire combiné à un second élément binaire : 2 bits

Si maintenant on ajoute au dispositif précédent une seconde ampoule L2 et un second interrupteur SW2, on multiplie par 2 le nombre de possibilités visuelles.

   

Le simple fait d'ajouter une troisième ampoule L3 et un troisième interrupteur SW3 va encore multiplier par deux le nombre de combinaisons possibles, et l'ajout d'une quatrième ampoule L4 et d'un quatrième interrupteur SW4 double encore le nombre de possibilités.

Bref, à chaque fois que l'on ajoute une composante de base (interrupteur + ampoule), on multiplie par deux le nombre de combinaisons. On ne dirait pas comme ça, mais avec quelques interrupteurs et quelques ampoules supplémentaires, on peut très vite atteindre un nombre de combinaisons très important.

A titre d'exemple, on peut atteindre 256 combinaisons possibles avec 8 ampoules (appelons-les désormais des bits), et 65536 combinaisons possibles avec 16 ampoules (16 bits). Il est aisé de dire qu'à chaque ampoule correspond le nombre 1 quand elle est allumée ou le nombre 0 quand elle est éteinte, mais ce n'est pas suffisant pour décrire pleinement le nombre que chaque combinaison représente. Si on reprend l'exemple précédent avec nos deux ampoules L1 et L2, on voit que l'on dispose d'un "code binaire brut" égal à 00, 01, 10 ou 11, mais ces nombres, qui correspondent à une notation en base 2, ne sont pas immédiatement représentatifs du nombre décimal (base 10) qui leur correspond et que l'on a plus d'aisance à manipuler car plus commun dans nos activités de tous les jours. C'est pourquoi on doit faire correspondre à chaque ampoule (à chaque bit) une valeur qui lui est sienne et qui n'appartient à aucune autre. A l'ampoule L1, on peut attribuer la valeur 1, et à l'ampoule L2 on peut attribuer la valeur 2. On peut ensuite additionner la valeur des ampoules allumées, et ne pas du tout tenir compte des ampoules éteintes. Cela pourrait donner la chose suivante :

   

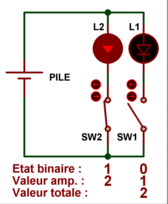
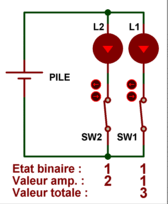
Si les deux ampoules sont éteintes, on obtient une valeur totale égale à 0 car aucune des valeurs propres à chaque ampoule n'est prise en compte, elles sont toutes ignorées. Si l'ampoule L1 est seule allumée, on ne tient compte que de sa valeur propre, qui est égale à 1. Si l'ampoule L2 est seule allumée, on ne tient compte que de sa valeur propre, qui est égale à 2. Et si les deux ampoules L1 et L2 sont allumées, on additionnent entre elles les deux valeurs de 1 et 2, ce qui donne 3. Nous disposons bien de 4 valeurs totales (décimales) possibles, avec 2 ampoules seulement (2 bits), ces valeurs peuvent être comprises entre 0 et 3. 

Écriture en 8 bits

Si maintenant nous utilisons 8 ampoules (8 bits), le nombre de combinaisons possibles est de 256. Nous n'allons pas dessiner toutes ces combinaisons car l'encre d'imprimante coûte cher, mais nous pouvons prendre un exemple parmi d'autres, schématisé sur le croquis suivant.



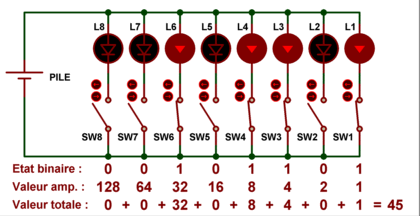
Si on ne prend en compte que les lampes allumées et que l'on additionne leurs valeurs respectives, on aboutit à la somme totale de 45. En effet, rien de plus simple, il suffit de raisonner de la façon suivante :

- La valeur totale vaut pour le moment 0 (zéro)

- La lampe L1 est allumée, on ajoute sa valeur qui est 1 à la valeur totale actuelle qui est 0 : on obtient la valeur totale de 1

- La lampe L2 est éteinte, on n'ajoute rien à la valeur totale actuelle qui est 1 : la valeur totale reste à 1

- La lampe L3 est allumée, on ajoute sa valeur qui est 4 à la valeur totale actuelle qui est 1 : on obtient la valeur totale de 5

- La lampe L4 est allumée, on ajoute sa valeur qui est 8 à la valeur totale actuelle qui est 5 : on obtient la valeur totale de 13

- La lampe L5 est éteinte, on n'ajoute rien à la valeur totale actuelle qui est 13 : la valeur totale reste à 13

- La lampe L6 est allumée, on ajoute sa valeur qui est 32 à la valeur totale actuelle qui est 13 : on obtient la valeur totale de 45

- La lampe L7 est éteinte, on n'ajoute rien à la valeur totale actuelle qui est 45 : la valeur totale reste à 45

- La lampe L8 est éteinte, on n'ajoute rien à la valeur totale actuelle qui est 45 : la valeur totale reste à 45

C'est ainsi qu'on en déduit qu'un nombre binaire écrit "00101101" (c'est ce qu'on lit pour les lampe en partant de L8 en allant vers L1) est équivalent en valeur au nombre décimal écrit "45". Autre exemple :



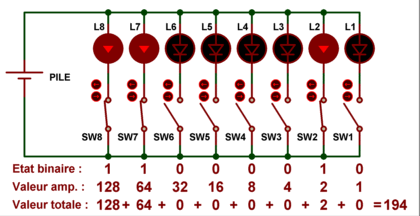
Si comme précédemment on ne prend en compte que les lampes allumées et que l'on additionne leurs valeurs respectives, on aboutit à la somme totale de 194. 

- La valeur totale vaut au départ 0 (zéro)

- La lampe L1 est éteinte, on n'ajoute rien à la valeur totale actuelle qui est 0 : la valeur totale reste à 0

- La lampe L2 est allumée, on ajoute sa valeur qui est 2 à la valeur totale actuelle qui est 0 : on obtient la valeur totale de 2

- La lampe L3 est éteinte, on n'ajoute rien à la valeur totale actuelle qui est 2 : la valeur totale reste à 2

- La lampe L4 est éteinte, on n'ajoute rien à la valeur totale actuelle qui est 2 : la valeur totale reste à 2

- La lampe L5 est éteinte, on n'ajoute rien à la valeur totale actuelle qui est 2 : la valeur totale reste à 2

- La lampe L6 est éteinte, on n'ajoute rien à la valeur totale actuelle qui est 2 : la valeur totale reste à 2

- La lampe L7 est allumée, on ajoute sa valeur qui est 64 à la valeur totale actuelle qui est 2 : on obtient la valeur totale de 66

- La lampe L8 est allumée, on ajoute sa valeur qui est 128 à la valeur totale actuelle qui est 66 : on obtient la valeur totale de 194

Ainsi, un nombre binaire écrit "11000010" est équivalent en valeur au nombre décimal écrit "194".

Remarques
- Les lampes et interrupteurs sont numérotés de 1 à 8, mais il est aussi commun dans la profession de les numéroter de 0 à 7. Cela ne change strictement rien à la façon de "décoder" la valeur binaire pour en obtenir son équivalent décimal, mais peut parfois embrouiller les esprits. Ne vous laissez pas faire !

- La lampe numérotée L1 est ce qu'on appelle le poids faible, car sa valeur propre est la plus petite de toutes les lampes. La lampe numérotée L8 est appelée le poids fort, car sa valeur propre est la plus grande de toutes les lampes. Si la lampe L8 est la seule allumée, le résultat final a plus de poids (128) que si seule la lampe L1 est allumée (résulta final de valeur 1).

Encore plus de bits !

Et on peut ainsi aller plus loin avec le nombre de bits, pour passer à 32 bits, 64 bits, 128 bits, 256 bits, etc. Avec 16 bits, nous disposons déjà de 65536 combinaisons (valeurs décimales) possibles, ce qui est déjà très confortable pour bien des applications. Comme la valeur (le poids) de la neuvième lampe L9 sera le double de celle qui la précède (lampe L8), sa valeur sera de 256 (128 ; 2). La valeur de L10 sera le double soit 512, et ainsi de suite jusqu'à la seizième ampoule L16 qui se voit attribuer la valeur de 32768.



Un nombre binaire écrit "0011001100000001" est équivalent en valeur au nombre décimal écrit "13057".

Notation hexadécimale

La notation hexadécimale permet d'écrire une valeur "longue" avec peu de caractères. Le principe de "réduction" visant à simplifier l'écriture d'un nombre binaire ou décimal est assez simple, il suffit de retenir qu'un caractère alphanumérique compris entre 0 et 9 ou compris entre A et F est attribuée à chaque paquet de 4 bits, ce qui explique que les octets sont toujours écrits sous la forme $xx (le symbole $ permet juste de spécifier qu'il s'agit d'un nombre exprimé en hexadécimal, il ne joue aucun rôle dans la valeur qui suit). Un octet comportant 8 bits, il est nécessaire d'utiliser deux caractères pour le décrire. La correspondance entre paquet de 4 bits, caractère hexadécimal et valeur décimale répond à ce qui suit :

0000 = 0 = 00
0001 = 1 = 01
0010 = 2 = 02
0011 = 3 = 03
0100 = 4 = 04
0101 = 5 = 05
0110 = 6 = 06
0111 = 7 = 07
1000 = 8 = 08
1001 = 9 = 09
1010 = A = 10
1011 = B = 11
1100 = C = 12
1101 = D = 13
1110 = E = 14
1111 = F = 15

Les exemples suivants montrent des correspondances entre nombres binaires, nombres hexa et nombres décimaux, il s'agit dans ce cas d'octets (8 bits) dont la valeur peut être comprise entre 0 et 255. 

00000000 = $00 = 0d
00111010 = $3A = 58d
11110001 = $F1 = 241d
11111111 = $FF = 255d

C'est bien gentil tout ça, il est effectivement très simple d'effectuer les conversions entre valeurs binaires et valeurs hexa. Mais comment effectuer la conversion directe entre hexa et décimal - dans un sens ou dans l'autre, sans passer par la valeur binaire ? 

Conversion hexa vers décimal d'un octet

C'est le plus simple. 

- on convertit le premier caractère alphanumérique (chiffre ou lettre) en son équivalent décimal grâce à la liste de conversion vue précédemment.

- on multiplie cette valeur par 16
- on convertit le second caractère alphanumérique en son équivalent décimal
- on additionne cette seconde valeur à celle obtenue ci-avant.

Exemple avec la valeur hexa $3F
- le caractère 3 en hexa correspond à la valeur 3 en décimal
- on multiplie la valeur décimale 3 par 16, on obtient 48
- le caractère F en hexa correspond à la valeur 15 en décimal
- on additionne les deux valeurs 48 et 15, on obtient la valeur 63.
$3F = 63d

Exemple avec la valeur hexa $B6
- le caractère B en hexa correspond à la valeur 11 en décimal
- on multiplie la valeur décimale 11 par 16, on obtient 176
- le caractère 6 en hexa correspond à la valeur 6 en décimal
- on additionne les deux valeurs 176 et 6, on obtient la valeur 182.
$B6 = 182d

Conversion décimal vers hexa d'un octet

Il existe plusieurs méthodes, voici la mienne :

- on divise la valeur décimale par 16, la partie entière correspond au premier caractère de la valeur hexa;

- on multiplie la partie fractionnaire (ce qu'il y a après la virgule) par 16, et on obtient le second caractère de la valeur hexa.

Exemple avec la valeur décimale 12

- on divise 12 par 16, on obtient une partie entière égale à 0, le première caractère hexa est donc 0.

- on multiplie la partie fractionnaire par 16, ce qui donne 0,75 ; 16 = 12, le second caractère hexa est donc C.

La valeur Hexa du nombre décimal 12 est donc $0C.

Exemple avec la valeur décimale 143

- on divise 143 par 16, on obtient une partie entière égale à 8, le première caractère hexa est donc 8.

- on multiplie la partie fractionnaire par 16, ce qui donne 0,9375 ; 16 = 15, le second caractère hexa est donc F.

La valeur Hexa du nombre décimal 12 est donc $8F.

Remarque : si la valeur décimale à convertir est strictement inférieure à 16, c'est encore plus simple, il suffit de convertir cette valeur en sa représentation hexa, et d'ajouter un 0 (zéro) devant. Par exemple, la conversion en hexa de la valeur décimale 8 est $08, et la conversion en hexa de la valeur décimale 15 est $0F.

Remplacement des ampoules par des fils d'entrée / sortie standards

Les petits schémas qui précèdent mettent en avant des lampes qui s'allument ou qui restent éteintes, mais on peut imaginer avoir à leur place, des pattes de circuits intégré (entrées logiques ou sorties logiques), par exemple. Dans ce cas, la mesure de tension faite sur chaque patte renseigne sur l'état logique de chacune d'elle, il est d'usage de trouver du +5 V pour un état logique haut (1, lampe allumée) et de trouver 0 V pour un état logique bas (0, lampe éteinte). Mais dans la pratique, ces valeurs peuvent bien sûr différer un petit peu (quelques millivolts d'écart), voir s'en écarter totalement si la tension d'alimentation des circuits intégrés n'est pas de 5 V mais de 3,3 V ou moins. Mais la règle générale veut qu'un circuit intégré logique alimenté sous une tension de X volts présente une tension égale à ou voisine de X volts sur ses sorties placées à l'état haut, et présente une tension égale à ou voisine de 0 V pour les sorties placées à l'état bas. Il en est de même pour les entrées, qui doivent recevoir une tension égale à ou voisine de X volts pour un état haut et une tension égale à ou proche de 0 V pour un état bas.