Appareils de mesure à courant continu
Dans cette section, nous couvrons le principe de fonctionnement de quelques appareils de mesure à courant continu qui sont souvent rencontrés dans l'industrie. Nous limiterons l'étude aux instruments à affichage analogique, c'est à dire ceux ayant une aiguille qui se déplace devant un cadran gradué.
Les appareils à affichage numérique possèdent essentiellement les mêmes propriétés, mais ils indiquent en chiffres la grandeur mesurée.
Le mouvement d'Arsonval
La plupart des voltmètres et des ampèremètres à courant continu contiennent un élément de base appelé mouvement d'Arsonval.
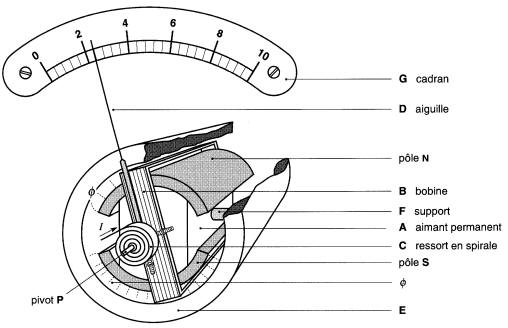
Ce mouvement sert à faire dévier l'aiguille de l'instrument et il comprend les parties suivantes (Fig. 6-1):
Figure 6-1 Composants d'un mouvement d'Arsonval

a) un aimant permanent A possédant deux pièces polaires N et S en fer doux.
L' aimant produit un champ magnétique 0;
b) une bobine mobile B en forme de cadre, composée de quelques centaines de spires de fil très fin.
La bobine est très légère et elle est soutenue par deux pivots d'acier P qui tournent entre deux diamants ;
c) deux ressorts en spirale C qui s'opposent à la rotation de la bobine.
Les deux ressorts sont reliés aux extrémités de la bobine et servent à y amener le courant I;
d) une aiguille D fixée au cadre;
e) un noyau de fer doux cylindrique E concentre le champ magnétique créé par l'aimant. L'aimant est fixé au noyau par le support F; un cadran gradué G. La position de l'aiguille devant les divisions du cadran donne la valeur du courant ou de la tension mesurée.
Si aucun courant ne traverse le cadre, les ressorts en spirale maintiennent celui-ci dans une position telle que l'aiguille indique zéro sur le cadran.
Lorsqu'un courant traverse les conducteurs de la bobine, les forces électromagnétiques qui résultent de l'action du champ magnétique 0sur le courant font tourner le cadre, tout en agissant contre la force de torsion des ressorts.
L' origine de ces forces électromagnétiques est expliquée dans la section Forces électromagnétiques.
La déviation du cadre, enregistrée par la déviation de l'aiguille, est d'autant plus considérable que le courant est plus fort: elle peut donc servir à la mesure du courant.
Si l'on inverse le sens du courant dans le cadre, le sens de rotation du cadre change.
On incorpore au mouvement un système d'amortissement afin que l'aiguille prenne rapidement sa position finale.
Sinon, il faudrait attendre plusieurs secondes avant qu'elle cesse d'osciller autour de sa position d'équilibre.
Selon sa construction, le mouvement d'Arsonval peut donner une déviation complète de l'aiguille pour des courants aussi faibles qu'un milliampère, parfois de 50 mA seulement.
Cependant, la bobine peut supporter des courants valant plusieurs fois celui qui provoque la pleine déviation.
Par exemple, la bobine d'un mouvement de 1 mA, possédant habituellement une résistance de 50 ohms, dissipe seulement 50 µW lorsqu'elle porte son courant nominal.
Une puissance aussi faible provoque une augmentation de température inférieure à 1 °C.
La bobine peut donc supporter, sans dommage thermique, des courants de l'ordre de 5 à 10 fois le courant nominal. Lorsque le cadran est gradué directement en milliampères, l'instrument porte le nom de milliampèremètre.
Mesure des courants intenses; ampèremètre
Il ne serait pas pratique de fabriquer une bobine de fil assez gros pour supporter les courants intenses que l'on rencontre dans l'industrie, car elle serait lourde et, par suite, très peu sensible.
On contourne la difficulté en plaçant en parallèle avec un mouvement d'Arsonval un conducteur de très basse résistance appelé shunt (Fig. 6-2).
Figure 6-2 Montage d'un shunt de 100 A et d'un milliampèremètre
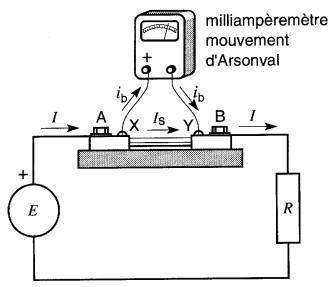
De cette façon, la plus grande partie du courant à mesurer passe par le shunt (qui offre moins d'opposition au passage du courant), et une fraction constante du courant total est déviée dans l'instrument de mesure. L'ensemble du shunt et du mouvement d'Arsonval porte le nom d'ampèremètre.
La Fig. 6-3a montre deux shunts constitués de deux blocs de cuivre portant des vis de serrage et reliés par plusieurs lames de manganine.
Figure 6-3a Shunts de 2000 A et de 100 A
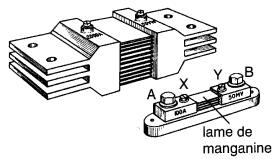
Ce matériau est utilisé car sa résistance demeure rigoureusement constante, quelle que soit la température. Le shunt se monte en série dans le circuit d'utilisation dans lequel on veut mesurer le courant, tandis que le milliampèremètre (mouvement d' Arsonval) est raccordé en parallèle avec le shunt.
La Fig. 6-2 montre les bornes A et B du shunt intercalées dans le circuit en question et le milliampèremètre raccordé entre les points X et Y du shunt. Lorsque le shunt porte son courant nominal, la chute de tension entre les bornes X et Y est généralement de 50 mV.
Le courant I qui traverse le circuit d'utilisation se divise en deux parties: la plus grande partie IS passe dans le shunt et une faible partie ib est dérivée dans le milliampèremètre.
Si le courant I dans le circuit double, les courants ib dans l'instrument et I, dans le shunt doublent également.
Le rapport des courants reste donc constant, quelle que soit la valeur de I. La déviation de l'aiguille causée par ib peut donc servir à la mesure de I. Pour les instruments usuels, le zéro de l'échelle est placé à l'extrémité gauche.
On ne peut donc faire passer le courant que dans un sens déterminé. Une des bornes est toujours marquée d'un signe (+):
si le courant entre par cette borne, l'aiguille dévie dans le bon sens;
si le courant circule en sens inverse l'aiguille tend à dévier vers la gauche, mais elle est arrêtée par une petite tige sans toutefois être endommagée.
Remarques sur les shunts
Pour des intensités de courant inférieures à 20 A, le shunt est logé à l'intérieur du boîtier de l'ampèremètre ; pour des intensités plus grandes, le shunt est placé à l'extérieur.
Dans le cas des ampèremètres de laboratoire, on utilise des jeux de shunts extérieurs.
Ceci permet la mesure des courants variant entre de très grandes limites (de 0,01 à 500 A par exemple) en changeant tout simplement les shunts, lesquels sont relativement peu coûteux.
Les shunts industriels sont construits pour mesurer des courants pouvant atteindre 10 000 A.
Même si la chute de tension correspondante n'est que de 50 mV, la puissance dégagée pour une telle intensité est de 500 W, ce qui requiert une bonne ventilation, assurée par la structure lamellée des plaques de manganine (Fig. 6-3b).
Figure 6-3b
Shunt de 10 000
A, 50 mV, ayant une précision de 0,25 %. Dimensions: 330 x 200 x 100 mm; masse:
32 kg

L' exemple numérique suivant illustre la méthode à suivre pour calculer un shunt, connaissant
1) la valeur du courant qui donne une déviation complète de l'aiguille;
2) la résistance du mouvement d'Arsonval et 3) l'intensité du courant à mesurer.
Exemple 6-1
L'aiguille d'un milliampèremètre se rend au bout de son échelle quand un courant de 10 mA circule dans la bobine.
Sachant que la résistance de cette bobine est de 15 ohms, quelle doit être la résistance du shunt qui permettra de transformer l'instrument en un ampèremètre calibré de 0 à 50 A?
Solution
On désire évidemment que l'aiguille se rende au bout de l'échelle quand il passe 50 A dans le circuit d'utilisation (Fig. 6-4).
Figure 6-4 Calcul d'un shunt (voir exemple 6-1)
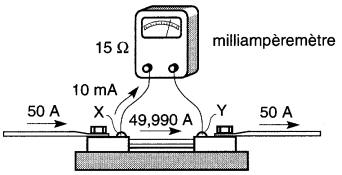
Puisqu'un courant de 10 mA donne une déviation complète, le courant principal de 50 A devra se partager comme suit:
10 mA (ou 0,010 A) dans la bobine et (50 -0,010) = 49,990 A dans le shunt.
La résistance de la bobine étant de 15 ohms, un courant de 10 mA y crée une chute de tension
E= RI = 15x0,010 = 0,15V
La bobine et le shunt étant en parallèle, cette même différence de potentiel existe aux bornes X, Y du shunt.
Le shunt traversé par un courant de 49,990 A sous une tension de 0,15 V doit avoir une résistance de:
R = E/I = 0,15 V / 49,990 A = 0,003Ω = 3 mΩ
Voltmètre
On obtient un voltmètre à courant continu en plaçant une résistance élevée en série avec un mouvement d' Arsonval (ou un milliampèremètre), identique à celui utilisé dans les ampèremètres.
Pour obtenir un ampèremètre, une basse résistance ou shunt était disposée en parallèle avec le milliampèremètre.
Pour mesurer la différence de potentiel entre les bornes d'une source, on branche le voltmètre directement entre les bornes (Fig. 6-5).
Figure 6-5 Composants d'un voltmètre
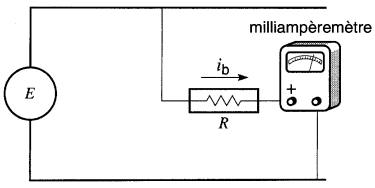
Une des bornes du voltmètre porte toujours un signe (+).
Lorsque cette borne est connectée du côté (+) de la tension que l'on veut mesurer, l'aiguille dévie dans le bon sens ; autrement, elle dévie dans le sens inverse. Le signe (+) sur le voltmètre permet donc d'identifier la polarité de la source.
D'après la loi d'Ohm I = E/R, si la tension E aux bornes de l'instrument double, le courant ib double, car la résistance de l'instrument est constante.
Ce courant ib, en doublant, produit une déviation de l'aiguille deux fois plus grande; la déviation de l'aiguille peut ainsi servir à la mesure de la tension.
La résistance R est ordinairement logée dans le boîtier du voltmètre.
Exemple 6-2
La bobine d'un milliampèremètre a une résistance de 10Ω et donne une déviation maximale de l'aiguille lorsqu'elle est parcourue par un courant de 5 mA.
Quelle résistance extérieure faut-il brancher en série avec cette bobine pour transformer l'instrument en un voltmètre calibré de 0 à 150 V?
Solution
On désire que l'aiguille donne une déviation complète pour une tension de 150 V appliquée entre les points A et B (Fig. 6-6).
Figure 6-6 Calcul de la résistance d'un voltmètre (voir exemple 6-2)
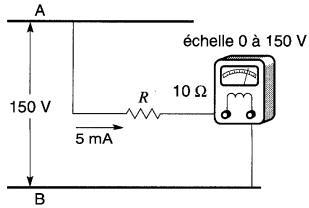
Pour cela, il faut qu'un courant de 5 mA (0,005 A) passe dans la bobine.
Alors, une tension de 150 V entre A et B doit faire circuler un courant de 0,005 A.
La résistance entre ces deux points doit donc être:
R = E/I = 150 V / 0,005 A = 30 000Ω = 30 kΩ
Puisque la résistance totale du voltmètre doit être de 30 000Ω et que celle de la bobine est de 10Ω, il faut disposer une résistance extérieure R de (30 000 - 10) = 29 990Ω en série avec le mouvement d'Arsonval.
En pratique, une résistance de 30 kΩ ayant une précision de 1 % serait acceptable.
Sensibilité d'un voltmètre
Du point de vue électrique, un voltmètre se comporte comme une résistance élevée lorsqu'il est raccordé à deux points d'un circuit pour la mesure de la tension entre ces points.
Considérons, par exemple, le circuit de la Fig. 6-7 composé de deux résistances RI et R2 raccordées en série sur une source E.
Figure 6-7 Mesure de la tension entre les points 1 et 2
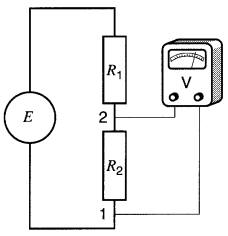
Lorsqu'on branche un voltmètre aux bornes de la résistance R2, on place effectivement une résistance élevée (voltmètre) en parallèle avec R2.
Bien que la présence du voltmètre ait un effet négligeable dans les circuits industriels, elle peut cependant entraîner des erreurs de mesure très appréciables dans les circuits électroniques où les résistances RI et R2, par exemple, auraient des valeurs très élevées.
Figure 6-8 Effet du voltmètre sur la tension à mesurer
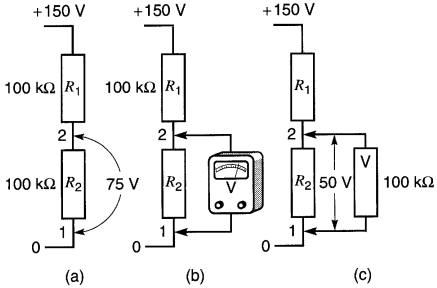
Pour illustrer, considérons le circuit composé de deux résistances de 100 kΩ groupées en série et alimentées par une source de 150 V (Fig. 6-8a).
Puisque les résistances ont la même valeur, la tension aux bornes de chacune est évidemment de 75 V.
Branchons maintenant aux bornes de R2 un voltmètre gradué de 0 à 100 V ayant une résistance totale de 100 kQ2. En étudiant les schémas des figures 6-8b et 6-8c, on constate que la résistance effective entre les bornes 1 et 2 n'est plus de 100 kΩ mais seulement de 50 kΩ.
La présence du voltmètre dans le circuit a donc modifié la résistance totale du circuit. Un calcul rapide nous indique que la tension aux bornes de la résistance R2 de la Fig. 6-8c tombe à 50 volts: c'est cette valeur qui sera indiquée par le voltmètre.
Une personne non avertie pourrait conclure, à tort, que la tension aux bornes deR2est de 50 volts même quand le voltmètre n'y est pas branché.
Si un voltmètre de même graduation, mais ayant une résistance beaucoup plus élevée (10 MΩ par exemple), avait été employé pour la mesure de la tension aux bornes de R2, son indication aurait été assez près de 75 V.
Ceci résulte du fait que la présence d'une résistance de 10 MΩ groupée en parallèle avec la résistance R2 de 100 kΩ n'aurait pratiquement pas modifié la valeur de la résistance entre les points 1 et 2 du circuit.
On dit alors que ce second voltmètre est plus sensible que le premier, parce que sa résistance est plus élevée.
La sensibilité d'un voltmètre dépend du courant requis pour produire une déviation complète. Elle est exprimée en ohms/volt et on la trouve par le rapport :

Ainsi, la sensibilité d'un voltmètre ayant une calibration de 0 à 100 V et une résistance de 100 000Ω est :
sensibilité = 100 000 Ω =100 V = 1000 ohms/volt.
La sensibilité d'un voltmètre à échelles multiples est la même pour chacune des échelles. La meilleure sensibilité que l'on puisse obtenir avec un voltmètre à mouvement d'Arsonval est de l'ordre de 50 000 Q/V.
Les voltmètres électroniques permettent d'obtenir des sensibilités bien supérieures, atteignant 10 MΩ/V, mais leur emploi n'est indispensable que pour mesurer des tensions aux bornes de résistances élevées comme celles rencontrées dans les montages électroniques (Fig. 6-9).
Figure 6-9
Multimètre
électronique à affichage numérique. Cet instrument, construit avec des circuits
à l'état solide, ne contient aucun mouvement d'Arsonval. Comme voltmètre, il a
une précision de 0,1 % et une résistance de 10 MΩ

Précision d'un voltmètre
La précision d'un appareil de mesure est l'exactitude avec laquelle l'instrument indique cette mesure. On l'exprime habituellement en % de la graduation maximale de l'échelle. Il ne faut pas confondre la sensibilité d'un instrument avec sa précision.
Ainsi, la sensibilité d'un voltmètre dépend de l'intensité du courant qui produit la déviation complète de l'aiguille tandis que sa précision dépend du soin apporté à sa fabrication.
L'exemple suivant illustre l'effet de la précision sur l'erreur maximale d'une lecture d'instrument.
Exemple 6-3
Un voltmètre calibré 0 - 150 V possède une précision de ± 2%.
S'il indique 60 V lorsqu'il est raccordé à un circuit, à quelle erreur maximale doit-on s'attendre
Solution
Étant donné que l'appareil est gradué de 0 à 150 V, l'erreur de l'instrument pour n'importe quelle indication sur le cadran est:
± 2 % x 150 V = ± 3 V.
Quand l'instrument indique 60 V, la tension réelle du circuit peut avoir toute valeur comprise entre:
(60+3) = 63V et (60-3) = 57V
Cela représente une erreur possible de 3V / 60V = ± 0,05 = ± 5 %
Cette erreur possible dans la lecture est 2,5 fois plus grande que la précision spécifiée par le manufacturier de l'instrument.
Cet exemple démontre que l'on doit se méfier des lectures fournies par un instrument lorsque la déviation de l'aiguille représente une faible portion de l'échelle complète.
Ohmmètre
Nous avons déjà expliqué, comment l'on peut déterminer la valeur de la résistance d'un corps au moyen d'un ampèremètre, d'un voltmètre et d'une source de courant.
Il est possible de mesurer directement sa résistance, sans recourir à une source extérieure, avec un instrument de mesure appelé ohmmètre.
La construction de cet appareil, dans sa forme la plus simple, est donnée à la Fig. 6-10.
Figure 6-10 Construction d'un ohmmètre
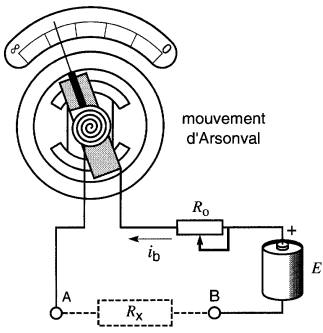
Il est constitué essentiellement d'un milliampèremètre dont l'échelle est calibrée de zéro ohm à l'infini (∞), d'une pile sèche de tension E et d'une résistance variable Ro.
Si l'on raccorde un élément extérieur Rx aux bornes A et B, l'aiguille s'arrêtera à une position intermédiaire entre les valeurs extrêmes 0 et ∞ et l'échelle indiquera directement la valeur de sa résistance.
Afin de mesurer avec assez de précision des résistances très différentes, on construit des ohmmètres à plusieurs échelles.
II faut calibrer l'appareil avant de l'utiliser, car la tension de la pile sèche varie avec le temps.
Pour la calibration, on procède comme suit:
on court-circuite les bornes A et B (ce qui équivaut à mesurer une résistance extérieure de valeur nulle) et on ajuste la résistance variable Ro pour que l'aiguille indique zéro (0). S'il est impossible d'obtenir ce résultat, il faut alors changer la pile.
Quand rien n'est raccordé entre A et B, l'aiguille doit indiquer une résistance infinie (∞); puisque la résistance est infiniment grande, il ne passe pas de courant dans l'instrument.
Mégohmmètre (Megger)
Le mégohmmètre est un ohmmètre conçu spécialement pour mesurer les résistances très élevées allant de 1 MΩ à 1000MΩ et plus.
On l'utilise pour vérifier la résistance à la masse des circuits électriques et pour tester la qualité de l'isolant des enroulements de machines.
Pour cette raison, la tension de la source interne, au lieu d'être de quelques volts seulement comme dans le ans d'un ohmmètre ordinaire, est plutôt de l'ordre de 500V et peut même aller jusqu'à 10 kV dans certains modèles.
Cette tension est générée en tournant une manivelle solidaire d'une petite génératrice à courant continu localisée à l'intérieur de l'appareil (Fig. 6-11).
Figure 6-11 Mégohmmètre de 500 V avec génératrice interne pouvant mesurer des résistances de zéro jusqu'à 100 MΩ

D'autres instruments développent la tension requise grâce à un circuit électronique qui multiplie plusieurs centaines de fois la tension générée par une pile sèche.
Pont de Wheatstone
Quand on doit mesurer la valeur d'une résistance avec une grande précision, on a recours au pont de Wheatstone.
Il est constitué d'une source à courant continu E, de trois résistances, R1, R2 et R3 de haute précision, et d'un microampèremètre (appellé galvanomètre).
La résistance inconnue Rx est connectée dans une des branches du pont comme le montre la Fig. 6-12.
Figure 6-12 Pont de Wheatstone pour mesurer la résistance avec une grande précision
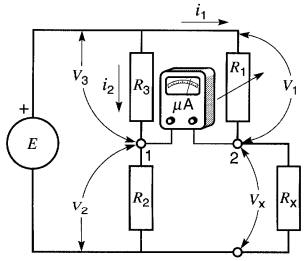
Pour mesurer sa valeur, on fait varier R1 jusqu'à ce que le courant passant dans le galvanomètre soit nul. On dit alors que le pont est équilibré. Les points 1 et 2 sont au même potentiel et on peut écrire les équations suivantes:
i2R2 = i1Rx (car V2 = Vx)
i2R3 = i1 R1 (car V3 = V1)
En résolvant ces équations, on trouve immédiatement que:
Rx = R1R2 / R3 (6-2)
La précision de la méthode de mesure dépend du fait que
1) la valeur de la résistance RX s'exprime en fonction de résistances connues avec une grande précision,
2) la valeur de la tension E de la source n'intervient pas dans le résultant et
3) la lecture sur le galvanomètre doit simplement être nulle.
Avec un pont de Wheatstone, on peut, sans difficulté, mesurer des résistances avec une précision de ± 0,01 %. 6.10
Résumé
Dans cette section nous avons appris comment sont construits les appareils de mesure à courant continu à affichage analogique.
Ils utilisent tous comme élément de base le mouvement d'Arsonval qui est un ampèremètre très sensible, donnant une pleine déviation pour des courants généralement inférieurs à 1 milliampère.
Pour obtenir un ampèremètre pouvant mesurer des courant supérieurs à celui donnant la pleine déviation du mouvement, on branche en parallèle avec celui-ci une résistance appelée shunt.
On réussit ainsi à mesurer des courants pouvant atteindre 100 kA. Ces shunts sont des résistances de précision ; les shunts prévus pour mesurer des courants intenses ( >20 A) sont branchés à l'extérieur du boîtier pour assurer une bonne ventilation.
Nous avons aussi appris comment calculer la résistance d'un shunt en utilisant la loi d'Ohm.
Pour obtenir un voltmètre, on branche en série avec le mouvement une résistance. La sensibilité d'un voltmètre est donnée en ohms/volt. C'est l'inverse du courant produisant la pleine déviation du mouvement.
Lorsqu'on effectue une mesure de tension dans un circuit comportant des résistances élevées on doit s'assurer que la sensibilité de l'appareil est suffisante pour ne pas perturber le circuit et fausser les mesures.
Nous avons vu aussi comment est construit l'ohmmètre utilisé pour mesurer les résistances. Cet appareil utilise une pile et une résistance branchées en série avec le mouvement.
La pile fait circuler un faible courant dans la résistance à mesurer et le mouvement affiche la valeur de la résistance en ohms.
Pour mesurer des résistances élevées (1 MΩ à 1000 MΩ) on utilise un mégohmmètre fonctionnant sur le même principe, mais dont la source de tension peut générer des tensions pouvant atteindre plusieurs kilovolts.
Enfin, pour mesurer des résistances avec une grande précision on utilise un pont de Wheatstone comprenant trois résistances de haute précision, un galvanomètre et une source de tension.
La mesure consiste à équilibrer le pont en faisant varier une de ses trois résistances. La résistance mesurée est alors fonction de trois résistances connues.
PROBLÈMES
Niveau pratique
6-1 Quelles sont les parties principales d'un mouvement d' Arsonval?
6-2 Comment peut-on déterminer la polarité d'une pile sèche?
6-3 À quoi servent les shunts? De quel alliage sont-ils constitués?
6-4 Comment un milliampèremètre peut-il servir à la mesure d'une tension?
6-5 Comment exprime-t-on la sensibilité d'un voltmètre?
6-6 Un instrument de mesure moins sensible qu'un autre peut-il être quand même plus précis?
6-7 À quoi sert l'ohmmètre? Quelles sont ses parties principales?
Niveau intermédiaire
6-8 Un voltmètre dont la sensibilité est de 100Ω/V a une précision de ± 0,1 %.
Quelle valeur de courant donne une déviation complète de l'aiguille?
6-9 La bobine d'un milliampèremètre a une résistance de 10Ω et un courant de 20 mA donne une déviation complète de l'aiguille.
Calculer les résistances des shunts à employer pour obtenir des déviations complètes avec des courants
a) de 100 mA et b) de 100 A?
6-10 La bobine d'un milliampèremètre a une résistance de 10 S2 et un courant de 20 mA donne une déviation complète de l'aiguille.
Quelle résistance doit-on raccorder en série avec ce milliampèremètre pour obtenir un voltmètre gradué de 0 à 150 V?
6-11 Un voltmètre gradué de 0 à 150 V donne une déviation complète lorsqu'il est parcouru par un courant de 1 mA. Sa résistance est de 150 kΩ. On désire le convertir en voltmètre gradué de 0 à 3 kV.
Trouver la valeur et la puissance de la résistance extérieure à ajouter.
6-12 Dans le problème 6-9, quelle doit-être la puissance de dissipation du shunt de 100 A?
Quelle est la puissance dissipée dans la bobine lors d'une déviation complète de l'aiguille?
6-13 Un voltmètre a une sensibilité de 2000 Ω/V.
Quel est le courant donnant une déviation complète?
6-14 Dans le circuit de la Fig. 6-7,R1=R2=200 kΩ et E = 240 V.
On désire mesurer la tension entre les points 1 et 2 au moyen d'un voltmètre à échelles multiples ayant une sensibilité de 1 kΩ,/V.
a) Quelle est la tension entre les points 1 et 2quand le voltmètre n'est pas raccordé?
b) Quelle sera la lecture du voltmètre si on utilise : 1) l'échelle 0-50 V? 2) l'échelle 0-300 V?
6-15 Dans le circuit de la Fig. 6-7, supposons que les résistances R1 et R2 aient maintenant une valeur de 100Ω et que E = 240 V.
On désire mesurer la tension entre les points 1 et 2 au moyen d'un voltmètre à échelles multiples ayant une sensibilité de 1 kΩ/V
Quelle est la tension mesurée entre les points 1 et 2 si on utilise l'échelle 0-50 V?
Niveau avancé
6-16 Deux voltmètres ayant une échelle de 0-150V ont une sensibilité de 10 kΩ/V et 20 kΩ/V respectivement. Si on les met en série aux bornes d'une source à 120 V, calculer la tension indiquée par chacun.
6-17 Les voltmètres électroniques à affichage numérique sont généralement plus précis et plus sensibles que les voltmètres à mouvement d' Arsonval.
Comment expliquer que ces voltmètres électroniques n'aient pas complètement remplacé les autres?
6-18 Un voltmètre gradué de 0 à 150V aune précision de ± 0,2 %. En vérifiant une pile sèche, on mesure une tension de 9,3 V.
Quelle est l'erreur maximale possible dans cette mesure (en volts)? Quel est le pourcentage d'erreur possible dans la lecture ?
6-19 Dans le problème 6-18, serait-il préférable de mesurer la tension de la pile avec un voltmètre de 0 à 15 V ayant une précision de ± 5 %?
Expliquer.
Réponses
8) 10 mA;
9a) 2,5Ω; 9b) 2Ω;
10) 7490Ω;
11) 2,85MΩ; 2,85 W;
12) 20W; 4 mW;
13) 500µA;
14a) 120 V; 14b) 40 V; 90 V;
15) 119,9 V;
16) 40 V et 80 V;
18) ± 0,3 V; ± 3,2%;
19) non, erreur = ± 8%
