Capacitance
Voir aussi : Condensateurs
On a vu à la section Phénomènes électrostatiques que lorsqu'on transfère une charge électrique d'un corps à un autre, une différence de potentiel ou tension s'établit entre eux.
De plus, la charge positive de l'un des corps est exactement égale à la charge négative de l'autre. Les expériences ont démontré que lorsque les corps demeurent fixes l'un par rapport à l'autre, la tension est proportionnelle à la quantité d'électricité transférée.
On peut donc écrire l'équation:
Ce rapport constant est appelé capacitance (symbole C). L'ensemble des deux corps et l'isolant qui les sépare constitue un condensateur.
Unité de capacitance - le farad
L'unité SI de capacitance est le farad(symbole F). Le farad est la capacitance d'un condensateur électrique entre les armatures duquel apparaît une différence de potentiel de 1 volt lorsqu'il est chargé d'une quantité d'électricité égale à 1 coulomb.
Plusieurs manuels français emploient le terme «capacité» au lieu de «capacitance», ce dernier étant plutôt employé dans les manuels américains. Cependant, nous utiliserons le terme capacitance pour caractériser l'effet capacitif, afin d'éviter toute confusion avec la capacité (puissance) des appareils électriques.
La relation donnant la capacitance est exprimée par la formule :
C = Q/E (21-1)
où
C= capacitance des deux corps, en farads [F]
Q = charge d'électricité sur chaque corps, en coulombs [C]
E = tension entre les deux corps, en volts 1[V]
Le farad est une unité beaucoup trop grande pour l'usage courant ; on emploie le plus souvent le microfarad (µF) ou le picofarad (pF), valant respectivement 1 µF =10-6 F et 1 pF =10-12 F.
Exemple 21-1
La différence de potentiel entre deux plaques ayant une capacitance de 100 microfarads (1 µF = 10-6 F) est de 200 volts. Combien de coulombs d'électricité ont été transférés'?
Solution
D'après la formule 21-1, on trouve :
Q = CE = (100 / 1 000 000) x 200 = 0.02 C
Formes de condensateurs
Le condensateur le plus simple est composé de deux plaques métalliques séparées par un isolant ou diélectrique (Fig. 21-1).
Figure 21-1 Deux corps conducteurs séparés par un isolant forment un condensateur
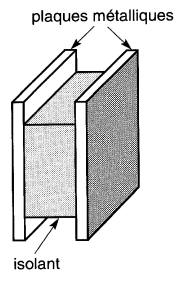
Le diélectrique peut être de l'air, du mica, du verre, du papier, etc., ou même le vide. La capacitance d'un tel condensateur dépend de trois facteurs:
1. la surface des plaques;
2. la distance entre les plaques;
3. la nature du diélectrique séparant les plaques.
La valeur de la capacitance de deux plaques séparées par un isolant est donnée par la formule:
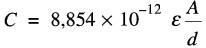(21-2)
où
C = capacitance, en farads [F]
ε = constante diélectrique de l'isolant [un nombre sans dimensions]
A = surface des plaques en regard, en mètres carrés [m²]
d = distance séparant les plaques, en mètres [m]
8,854 x 10-12 =permittivité du vide, une constante.
On peut donc doubler la capacitance d'un condensateur soit:
1. en doublant la surface de ses plaques ou
2. en réduisant de moitié la distance qui les sépare.
Noter que cette formule ne s'applique que si la distance d est petite par rapport aux dimensions des plaques.
Exemple 21-2
Deux plaques de 200 mm x 300 mm sont distantes de 1 cm dans l'air (Fig. 21-2).
Figure 21-2 Voir exemple 21-2
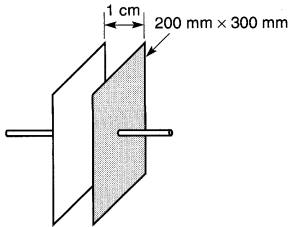
a) Calculer la capacitance en microfarads
b) Que devient la capacitance si la distance est réduite à I mm? (ε= 1 pour l'air)
Solution
a) D'après la formule (21-2),
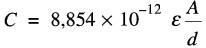
soit:
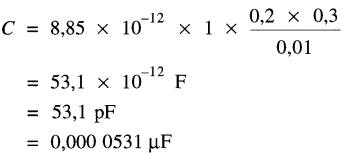
b) Lorsque la distance est réduite à 1 mm, la capacitance augmente de dix fois et elle devient 531 pF.
L' exemple précédent montre clairement qu'une grande surface de plaques et un faible écartement sont nécessaires pour obtenir une capacitance de quelques microfarads. Il est bon de noter que deux corps séparés par un isolant constituent toujours un condensateur.
Ainsi, les conducteurs d'une ligne de distribution forment un condensateur dont les «plaques» sont très longues, très fines et sont séparées par une distance considérable.
Un seul fil suspendu au-dessus du sol et isolé de ce dernier forme également un condensateur, une des plaques étant constituée par le fil même, et l'autre, par la terre.
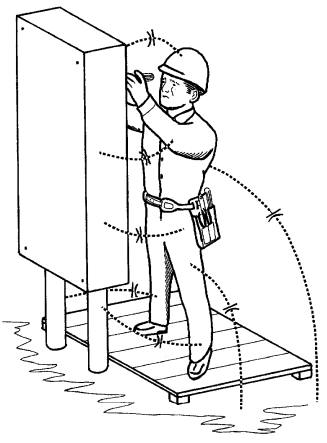
De la même façon, une personne se tenant debout sur une plateforme isolée produit avec la terre un condensateur dont la capacitance est de l'ordre de 200 picofarads (Fig. 21-3).
Figure 21-3 Une personne forme, avec la terre, un condensateur.
La personne constitue une des plaques, la plate-forme de bois et l'air sont les isolants, et la terre et les objets qui y sont raccordés constituent la deuxième plaque. Le schéma montre que la capacitance totale est composée de plusieurs petites capacitances en parallèle
Note: Le symbole électronique d'un condensateur est:
On trouvera aux sections ci-dessous les formules donnant la capacitance de paires de conducteurs de formes diverses.
Constante diélectrique
Nous avons vu que la capacitance d'un condensateur ne dépend pas seulement de sa forme ou de ses dimensions, mais aussi de la nature du diélectrique qui sépare ses plaques.
Si l'on intercale un isolant tel que le verre, le papier ou le mica entre les plaques d'un condensateur, sa capacitance devient plus grande que si l'isolant est de l'air.
La constante diélectrique e d'un isolant est le rapport entre la capacitance d'un condensateur construit avec cet isolant et la capacitance qu'il aurait si cet isolant était remplacé par le vide. La constante diélectrique est donc une propriété de l'isolant même.
Ainsi, la présence du papier qui a une constante diélectrique de l'ordre de 2,5 augmenterait de deux fois et demie la capacitance d'un condensateur auparavant isolé à l'air.
Le tableau 21-1 donne les valeurs approximatives de la constante diélectrique e de quelques isolants usuels, ainsi que leur rigidité diélectrique.
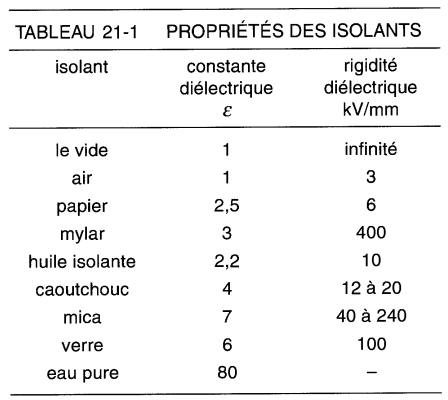
Une liste plus complète est fournie au tableau A-2.
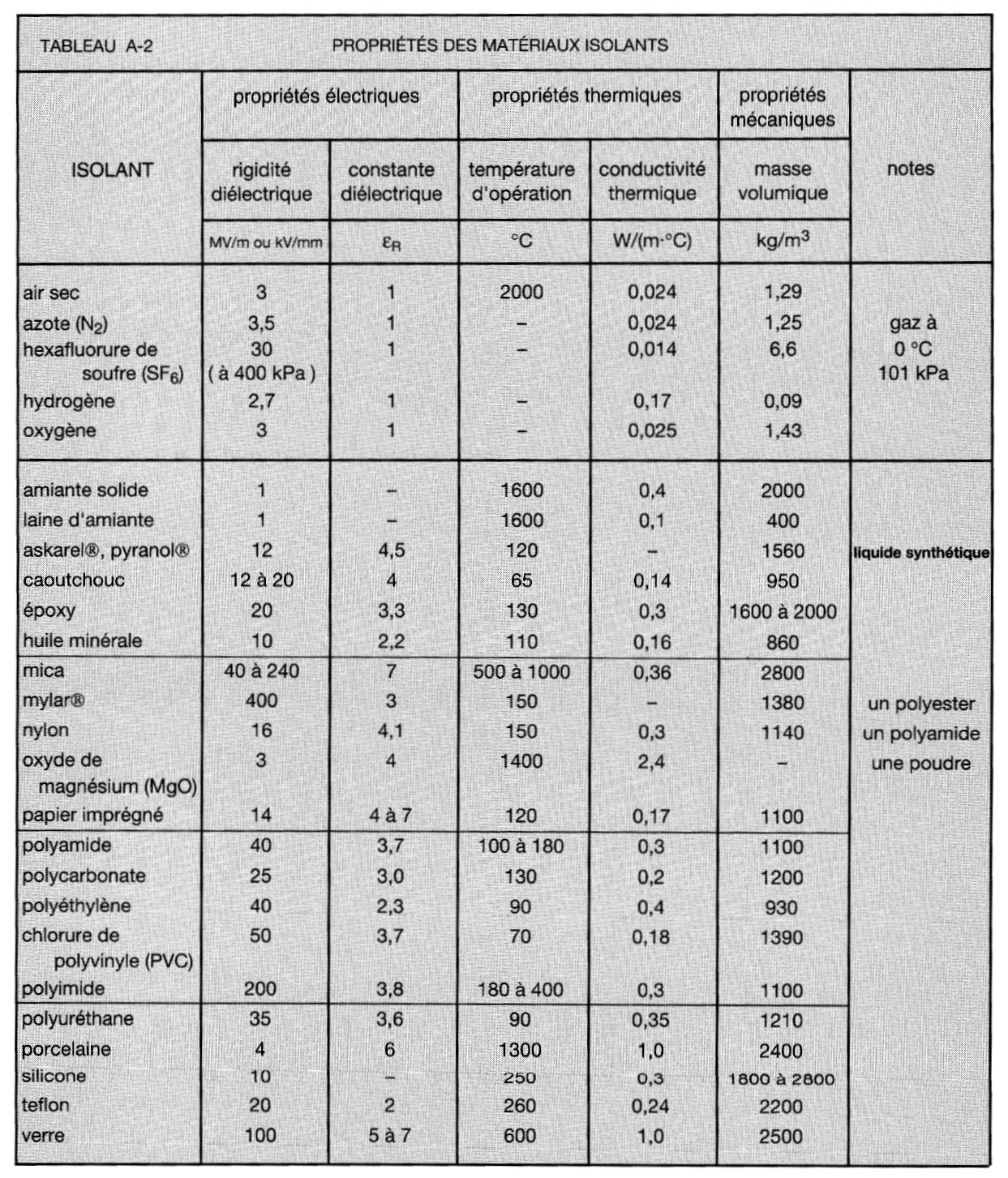
Tension de service, capacitance et dimensions d'un condensateur
On a vu qu'il est possible d'augmenter la capacitance d'un condensateur en réduisant l'épaisseur de l'isolant qui sépare ses plaques.
Cependant, si l'isolant est trop mince, il y a danger de claquage sous l'effet du champ électrique intense qui règne entre les plaques. Dans ce cas, un arc perce l'isolant et rend le condensateur inutilisable. La rigidité diélectrique de l'isolant est donc une autre caractéristique importante du diélectrique.
Un condensateur qui doit fonctionner sous une tension de 1000 V doit donc posséder entre ses plaques un diélectrique plus épais que celui d'un condensateur fonctionnant sous 20 V seulement.
Donc, pour une capacitance donnée, la surface des plaques d'un condensateur à tension élevée doit être plus grande que celle d'un condensateur à basse tension. Il s'ensuit qu'un condensateur de 40 µF, 600 V doit nécessairement être plus gros qu'un autre de 40 µF, 50 V.
Condensateurs en parallèle et en série
Lorsque deux ou plusieurs condensateurs sont branchés en parallèle (Fig. 21-4), la capacitance équivalente C de l'ensemble est égale à la somme des capacitances individuelles, soit:
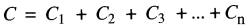(21-3)
Figure 21-4 Condensateurs raccordés en parallèle
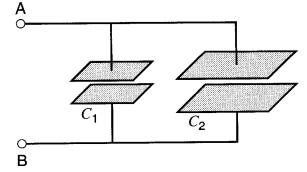
Lorsque deux ou plusieurs condensateurs sont branchés en série, la capacitance équivalente C de l'ensemble est donnée par l'expression:
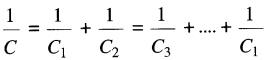(21-4a)
Figure 21-5 Condensateurs raccordés en série
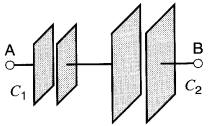
De cette formule, on déduit que la capacitance équivalente C de deux condensateurs en série (Fig. 21-5) ayant des capacitances C1 et C2 est donnée par:
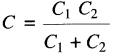(21-4b)
On doit retenir que lorsque les condensateurs sont raccordés en série, la charge électrique sur les plaques est la même pour chacun d'eux. De plus, elle est égale à la charge du condensateur équivalent C.
Exemple 21-3 Deux condensateurs de 4 µF et de 12 µF sont branchés en Série sur une source à c.c. de 600V (Fig.21-6).
Figure 21-6 Voir exemple 21-3
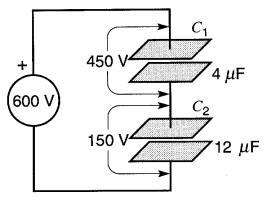
Calculer:
a) la capacitance totale
équivalente
b) la charge sur les plaques
c) la tension aux bornes de
chaque condensateur
Solution
a) La capacitance équivalente est :
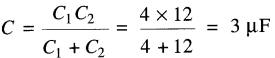
b) La charge électrique Q, accumulée sur les plaques du condensateur équivalent de 3 µF est donnée par la formule (21-1):
Q = CE = 3 x 10-6 x 600 = 0,0018 C
c) Puisque les condensateurs de 4 µF et de 12 µF sont en série, ils portent la même charge, soit 0,0018 C.
La tension aux bornes du condensateur de 4 µF vaut:
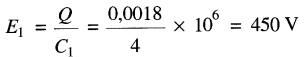
La tension aux bornes du condensateur de 12 µF vaut :
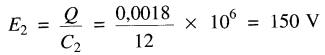
On vérifie immédiatement que la somme de ces deux tensions donne bien 450 + 150 = 600 V.
La répartition inégale de la tension totale entre les deux condensateurs peut avoir des conséquences fâcheuses.
Ainsi, s'ils sont construits pour supporter une tension de 300 volts, l'isolant du condensateur de 4 µF claquera sous la tension de 450 volts. Les plaques de ce condensateur seront aussitôt court-circuitées et la pleine tension de 600 volts sera appliquée au condensateur de 12µF, ce qui entraînera également sa destruction.
Énergie dans un condensateur
Il est facile de se rendre compte de l'énergie emmagasinée dans un condensateur chargé, car lorsqu'on le court-circuite, il se produit une forte étincelle. L'énergie emmagasinée est de l'énergie électrique (ou électrostatique) conservée dans le champ électrique entre les plaques; elle est restituée lors de la décharge.
Un condensateur peut donc agir comme charge ou comme source.
Voir : Réservoir Électronique
L'énergie emmagasinée dans un condensateur est donnée par l'équation:
W = CE² / 2
où
W = énergie, en
joules [J]
C = capacitance, en farads [F]
E = tension aux bornes, en volts
[V]
Ainsi, un condensateur de 300 µF chargé sous une tension de 400 V emmagasine une quantité d'énergie égale à:
W = CE² / 2= (300 x 10-6 x 400²) / 2= 24 J
Les meilleurs condensateurs industriels à courant continu emmagasinent environ 40 J/kg (énergie massique) ou 80 J/dm³ (énergie volumique).
À titre de comparaison, une batterie d'automobile emmagasine environ 80 kJ/kg ou 250 kJ/dm³, soit une énergie massique 2000 fois plus grande que pour un condensateur.
Condensateurs au papier, au plastique et à l'huile
Les condensateurs industriels sont formés par des minces feuilles de métal (telles que l'aluminium) séparées par une fine couche de papier ou une feuille de plastique synthétique. Les feuilles sont enroulées ensemble et forment un rouleau cylindrique qui est placé dans une enveloppe protectrice ou dans un boîtier. Les deux feuilles métalliques sont raccordées à ces bornes extérieures (Fig. 21-7).
Figure 21-7 Construction d'un condensateur conventionnel. Même si la superficie des plaques est très grande, l'encombrement est énormément réduit lorsque le tout est enroulé en forme de cylindre
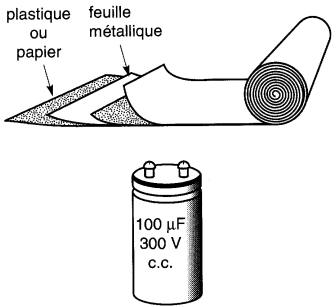
Les condensateurs destinés à supporter des tensions élevées sont imprégnés d'huile. La plupart de ces condensateurs sont installés sur les réseaux à courant alternatif; nous étudierons leurs propriétés à une section ci-dessous.
Condensateurs au plastique métallisé
Il est impossible de réaliser des feuilles de papier dont l'épaisseur est inférieure à 6 µm. Cependant, on peut, avec des plastiques et des laques appropriés, obtenir des rubans dont l'épaisseur ne dépasse pas 1 µm.
On recouvre ces rubans diélectriques extrêmement minces avec une couche métallique encore plus mince dont l'épaisseur est de l'ordre de 0,02 à 0,1 µm seulement.
À titre de comparaison, mentionnons que le diamètre d'un cheveu est de 50 µm environ.
Ces techniques permettent de réduire le volume d'un condensateur de 6 fois pour une même capacitance; c'est un avantage important lorsqu'il s'agit de construire des appareils de faibles dimensions.
Condensateurs électrolytiques
Les condensateurs électrolytiques représentent un effort ultime pour réduire l'épaisseur du diélectrique et augmenter la surface des plaques.
Les spécialistes en électrochimie ont découvert qu'il était possible de créer une mince couche d'oxyde d'aluminium sur une feuille d'aluminium en la passant dans un bain approprié en présence d'un courant électrique.
La couche ainsi déposée est extrêmement mince, mais sa propriété la plus importante est qu'elle constitue un isolant possédant une rigidité diélectrique de l'ordre de 600 kV/mm et une constante diélectrique de 10.
En rongeant la surface des feuilles d'aluminium on peut augmenter leur surface effective bien au-delà des dimensions apparentes.
Le diélectrique (oxyde d'aluminium) est en contact intime avec la plaque sur laquelle il a été formé ; il reste à établir un bon contact avec une deuxième plaque. On le réalise en imprégnant un papier poreux d'un liquide conducteur (électrolyte) que l'on intercale entre le diélectrique et une deuxième plaque en aluminium (Fig. 21-8).
Figure 21-8 Construction d'un condensateur électrolytique
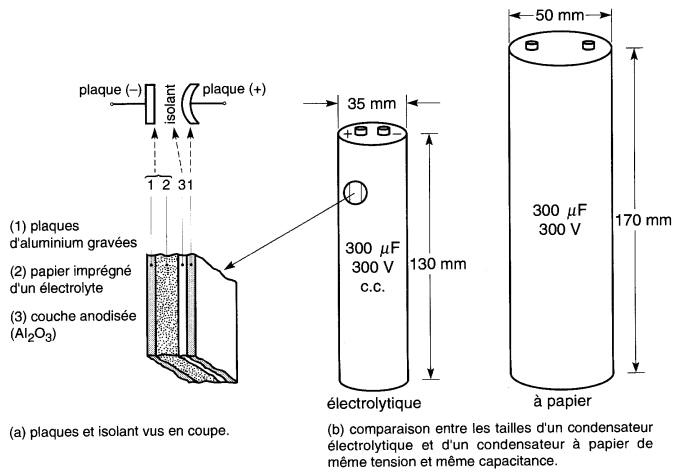
Les condensateurs ainsi formés ont une très grande capacitance par rapport à leur grosseur. Cependant, ils possèdent un inconvénient: lorsqu'on applique une tension, il faut s'assurer que la plaque portant l'oxyde d'aluminium soit positive (+).
Si l'on permute les polarités, il se produit une réaction électrochimique: l'électrolyte s'échauffe, des gaz sont libérés, la pression interne monte et le condensateur risque d'exploser. Les condensateurs électrolytiques sont donc polarisés et on ne peut pas les utiliser en courant alternatif.
Les bornes (+) et (-) sont indiquées sur le boîtier. La température ambiante doit être de l'ordre de 25 °C ou moins et la température du condensateur ne doit pas dépasser 40 °C car autrement sa durée de vie se trouve abrégée.
Si ces conditions sont respectées, un condensateur électrolytique peut atteindre une durée de vie de 10 ans. Lorsqu'on raccorde un condensateur électrolytique à une source de tension continue, et même après qu'il soit complètement chargé, un courant subsiste pendant un temps appréciable.
Ce courant, appelé courant de fuite, diminue avec le temps pour atteindre une valeur de régime permanent après une période de 15 à 30 minutes.
Ainsi, un condensateur de 1000 µF fonctionnant sous 350V peut tirer un courant de fuite initial de 100 mA qui se stabilisera aux environs de 10 mA. Cela représente des pertes Joule permanentes de 350V x 0,01A = 3,5W, qui font chauffer le condensateur.
Condensateurs électrolytiques à courant alternatif
On peut réaliser un condensateur électrolytique à courant alternatif (c.a.) en raccordant deux condensateurs électrolytiques à courant continu (c.c.) en série et en prenant soin de relier soit les deux bornes (+), soit les deux bornes (-) ensemble.
La capacitance ainsi formée vaut la moitié de la capacitance de l'un des condensateurs. Les condensateurs à c.a. fabriqués selon ce principe sont donc deux fois plus gros que ceux de même capacitance fonctionnant à courant continu seulement.
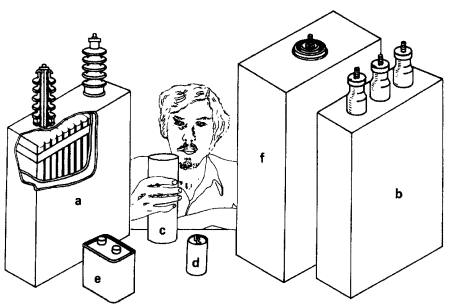
Ces condensateurs sont utilisés pour les moteurs monophasés à démarrage par condensateur. La Fig. 21-9 montre les spécifications de plusieurs types de condensateurs.
Figure 21-9 Dimensions relatives de six types de condensateurs.
(a) Condensateur monophasé au papier imprégné d'huile - 100 kvar, 14 400V, 60 Hz, 1,3 µF (pour lignes haute-tension). Dimensions: 460 mm x 340 mm x 115 mm.
(b) Condensateur triphasé au papier imprégné d'huile - 50 kvar, 600V, 60 Hz, 55 µF (pour corriger le facteur de puissance). Dimensions: 530 mm x 340 mm x 130 mm.
(c) Condensateur électrolytique
- 0,5 F, 6V c.c. (pour filtrer la tension des redresseurs électroniques).
Dimensions: 76 mm x 230 mm.
(d) Condensateur électrolytique
- 300 µF, 160V c.a. (pour démarrer les moteurs monophasés à c.a.).
Dimensions: 110mm x 60mm.
(e) Condensateur au papier - 40
µF, 440 V c.a. (pour moteur monophasé à condensateur permanent).
Dimensions: 140 mm x 115 mm x 75 mm. (
f) Condensateur au mylar - 5
µF, 30 kV (pour alimenter des éclateurs à haute puissance).
Dimensions : 610
mm x 360 mm x 180 mm.
Voir aussi : Description des condensateurs
Charge d'un condensateur
On a vu, à la section plus-haut, qu'il est possible de charger un condensateur, c'est-à-dire de transférer des électrons d'une plaque à l'autre, en le reliant aux bornes d'une source à courant continu.
Dans le schéma de la Fig. 21-10a, la source développe une tension de 128V et la borne b est négative par rapport à la borne a.
Figure 21-10
a. La source de 128V servira à charger le condensateur;
b. Condensateur en voie d'être chargé ;
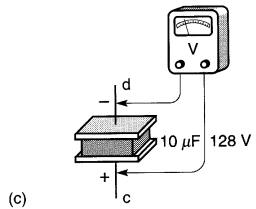
c. La tension subsiste aux bornes du condensateur. De l'énergie est emmagasinée dans le champ électrique entre les plaques.
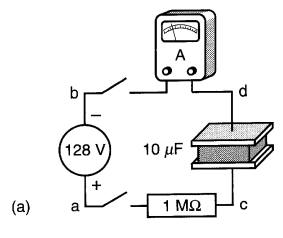
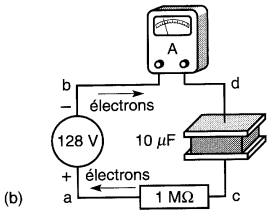
Il y a donc un surplus d'électrons sur la borne b. Le nombre d'électrons étant le même sur les deux plaques du condensateur, la tension entre ses bornes c et d est nulle. Lorsqu'on ferme l'interrupteur (Fig. 21-10b), les électrons de la borne b sont chassés vers la plaque d par répulsion mutuelle.
De plus, la charge positive de la borne a attire les électrons de la plaque c. Des électrons sont donc retirés de la plaque c et déposés sur la plaque d et, à mesure que ce transfert s'effectue, la tension aux bornes du condensateur croît.
Dans le cas de ce montage, l'augmentation de la tension est assez lente car le courant (taux de charge) est limité par la présence de la haute résistance série de 1 MΩ.
Dès que le nombre d'électrons transférés devient tel que la tension aux bornes du condensateur atteint celle de la source (128V), le déplacement des électrons cesse. Le condensateur est alors chargé complètement.
Si on ouvre l'interrupteur (Fig. 21-10c), les électrons restent prisonniers sur la plaque d, et la tension aux bornes du condensateur se maintient à 128V, même s'il n'est plus relié à la source.
Durant la charge d'un condensateur à travers une résistance, la tension aux bornes du condensateur suit une courbe exponentielle identique à celle décrivant la croissance du courant dans une bobine à travers une résistance (tableau 19-1 de la section Inductance).
Décharge d'un condensateur
Lorsque notre condensateur initialement chargé sous une tension de 128V est raccordé à une résistance R. la tension fait circuler un courant.
Ce courant résulte de l'écoulement des électrons de la plaque négative du condensateur vers la plaque positive (Fig. 21-12). À mesure que les électrons quittent la plaque d pour s'accumuler sur la plaque c, la tension aux bornes du condensateur diminue.
Elle atteint finalement une valeur nulle lorsque la charge sur les deux plaques devient nulle. Durant la décharge d'un condensateur dans une résistance, la tension à ses bornes suit une courbe exponentielle décroissante.
Constante de temps
Le temps requis pour charger ou décharger un condensateur dépend des valeurs de la résistance R et de la capacitance C. Tout comme dans le cas d'un circuit inductif, on définit une constante de temps τ pour un circuit capacitif, donnée par l'expression :
τ = RC (21-6)
où
τ
= constante de temps du circuit [s]
R = résistance du circuit [Ω]
C
= capacitance du circuit [F]
Ainsi, un circuit comme celui de la Fig. 21-10 formé d'un condensateur de 10 µF et d'une résistance de 1 MΩ possède une constante de temps τ de :
τ =RC= 1 MΩ x 10µF=10s
On associe également à la constante de temps, un demi-temps T0 donné par l'équation 19-9, soit :
T0 = 0,7 τ =0,7 x 10 = 7s
En utilisant le demi-temps T0, on peut tracer la tension en fonction du temps lors de la charge ou la décharge d'un condensateur.
Le temps de charge et lde décharge d'un condensateur est le principe de base des oscillateurs. Voir oscillateurs.
Courbes de charge et de décharge
La courbe de la Fig. 21-11 représente la tension en fonction du temps aux bornes du condensateur de 10 µF se chargeant à travers la résistance de 1 MΩ sous une tension de 128V.
Figure 21-11 Courbe de charge d'un condensateur. La tension aux bornes augmente de façon exponentielle
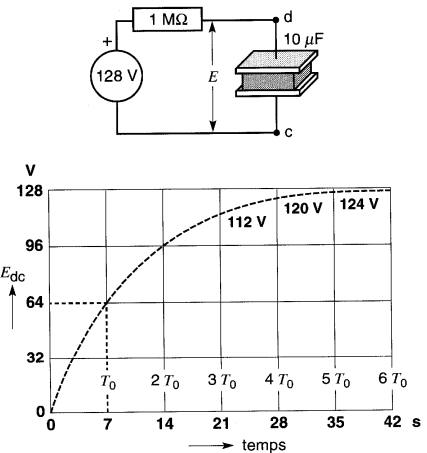
La courbe a été obtenue d'après la courbe universelle du tableau 19-1 section Inductance, sachant que:
Q1 = 0 V, Q2 = 128 V, Qd = Q2 - Q1 = 128V et T0 =7 s.
Les valeurs successives de la tension sont indiquées au tableau 21-2.
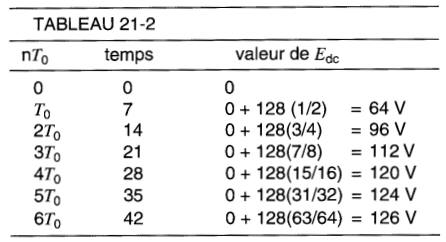
On peut considérer que le condensateur est pratiquement chargé après 6 T0 (98 % de la charge complète).
La courbe de la Fig. 21-12 représente la tension en fonction du temps aux bornes du condensateur de 10 µF chargé initialement à 128 V et se déchargeant à travers une résistance de 1 MΩ.
Dans ce circuit, T0 vaut encore 7 secondes. On constate que la tension n'atteint jamais une valeur nulle mais, en pratique, elle devient négligeable après un intervalle de 6 T0 secondes.
Cette courbe de la tension en fonction du temps a encore été obtenue en se servant de la courbe universelle présentée au tableau 19-1.
Dans ce cas, Q1 = 128V, Q2 = 0 V et Qd = Q2 - Q1 = -128V.
Les valeurs successives de la tension sont indiquées au tableau 21-3.
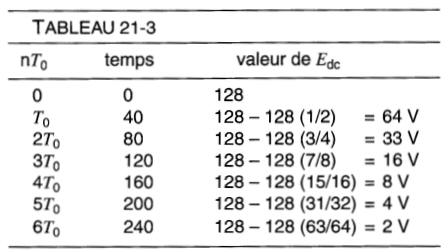
Loi fondamentale pour un condensateur
Quand la tension appliquée à un condensateur est fixe, il n'y a aucune circulation d'électrons d'une plaque à l'autre et, par conséquent, aucun courant électrique. Cependant, si la tension de la source augmente, le condensateur se charge davantage et, pendant cette période, le courant circule dans le circuit (Fig. 21-13).
Figure 21-13 Lorsque la tension augmente, le condensateur se charge et la source lui fournit de l'énergie
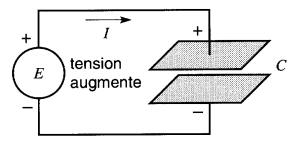
Puisque le courant entre par la borne (+) du condensateur, ce dernier constitue une charge. Le condensateur reçoit de l'énergie, et comme cette énergie n'est pas dissipée dans une résistance, elle est emmagasinée dans le condensateur.
De la même façon, quand la tension de la source diminue, le condensateur se décharge et le courant circule dans le sens inverse (Fig. 21-14).
Figure 21-14 Lorsque la tension diminue, le condensateur se décharge et la source reçoit de l'énergie du condensateur
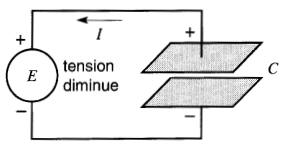
Puisque le courant sort de la borne (+), le condensateur est maintenant une source, fournissant de l'énergie à la «source» à laquelle il est branché.
Il est évident qu'un courant circule seulement lorsque la tension aux bornes du condensateur varie. La valeur du courant dépend à la fois du taux de variation de la tension et de la capacitance du condensateur. Cette loi fondamentale gouvernant le courant circulant dans un condensateur est exprimée par la formule :
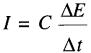(21-7)
où
I = courant, en
ampères [A]
C = capacitance, en farads [F]
ΔE = variation de
tension, en volts [V]
Δt = durée de la variation, en secondes [s]
Bien qu'elle ne porte pas de nom, cette loi est tout aussi fondamentale que la loi de Faraday E = L ΔI/Δt.
Exemple 21-4
La tension aux bornes du condensateur de 40 µF illustré à la Fig. 21-9e varie de 500V à 200V en 1 ms.
Calculer:
a) la valeur du courant pendant cet intervalle
b) la puissance débitée par le condensateur au début de l'intervalle
c) l'énergie débitée durant l'intervalle
Solution
On a: C = 40 µF
ΔE = (500 - 200) = 300V; Δt = 0,001 s
En reportant ces valeurs dans la formule 21-7, on trouve:
I = C (ΔE / Δt) = 40 x 10-6 x 300 / 0,001 = 12A
b) La puissance débitée par le condensateur au début de l'intervalle est:
P= EI =500V x 12A = 6000W
On constate que même s'il n'est pas très gros (140 x 115 x 75 mm), un condensateur peut fournir des puissances importantes durant de courtes périodes.
c) L'énergie emmagasinée dans le condensateur au début de l'intervalle est:
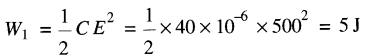
L'énergie emmagasinée à la fin de l'intervalle est :
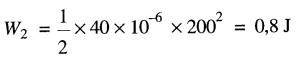
L'énergie libérée est donc :
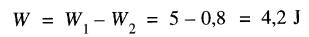
L'équation (21-7) entraîne des conséquences et des applications importantes.
Pour une capacitance donnée, on s'aperçoit que plus la tension change rapidement, plus le courant est grand. Le changement de tension est particulièrement rapide lorsqu'on branche un condensateur non chargé sur une source ES (Fig. 21-15).
Figure 21-15 Un courant énorme circule lorsqu'une tension est appliquée directement aux bornes d'un condensateur qui n'est pas chargé
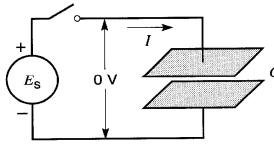
En un temps nul, la tension passe de zéro à une valeur E, de sorte qu'un courant I théoriquement infini circule à la fermeture de l'interrupteur.
En pratique, ce courant est limité par la résistance et l'inductance du circuit. Les contacts d'un interrupteur destiné à alimenter et à désalimenter un condensateur doivent donc être conçus pour supporter le courant intense de fermeture.
Cette propriété du condensateur d'absorber une énergie quasi instantanément est mise à profit dans la protection des gros moteurs contre les surtensions momentanées causées par la foudre, ou par l'ouverture et la fermeture des disjoncteurs du réseau.
En plaçant un condensateur de 0,2 µF à 0,5 µF en amont du moteur, on intercepte toute onde de choc venant de l'extérieur.
La charge transportée par l'onde est absorbée par le condensateur avant que la surtension atteigne les enroulements à l'intérieur de la machine (Fig. 21-16). Les condensateurs sont ainsi souvent employés comme protection supplémentaire en aval des parafoudres.
Figure 21-16 Protection de l'appareillage contre les ondes de choc. Noter l'amortissement de l'onde (a) par le parafoudre et ensuite (b) par le condensateur. L'onde de choc arrivant au moteur n'est plus dommageable pour les enroulements.
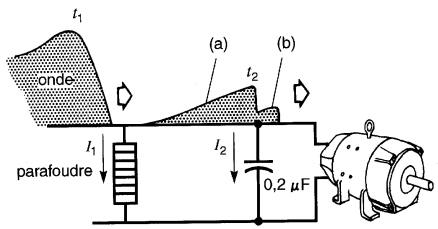
Tension variable sur un condensateur
La majorité des condensateurs fonctionnent sur des réseaux à courant alternatif où la tension varie périodiquement. Pour bien comprendre leur fonctionnement dans ces circonstances, il est utile d'analyser d'abord le comportement d'un condensateur soumis à une tension encore plus complexe, telle que celle donnée à la Fig. 21-17.
Figure 21-17 Tension variable aux bornes d'un condensateur et courant résultant
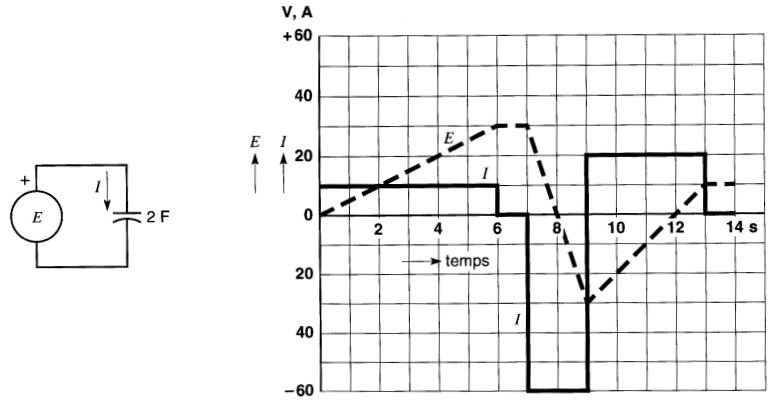
On se propose de trouver la valeur instantanée du courant lorsque la tension est appliquée à un condensateur de 2F. Rappelons que le courant est positif lorsqu'il circule dans le sens de la flèche.
Intervalle de 0 à 6 secondes. Pendant cette période, la tension varie de 0 à +30 volts. Sa pente est donc positive. Puisque la capacitance est de 2F, le courant I vaut:
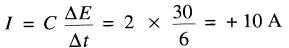
Le condensateur se charge, et le courant est positif. On note un point important: le courant est positif lorsque la pente de la tension est positive.
Intervalle de 6 à 7 secondes. Pendant cette période, la tension ne varie pas; donc ΔE/Δt = 0 et par conséquent I = 0.
Intervalle de 7 à 9 secondes. La tension diminue de +30V à -30V, soit une variation totale de -60V.
Le courant vaut donc:
Le courant est négatif pendant toute cette période, car la pente de la tension est toujours négative. Noter qu'entre 7 s et 8 s le condensateur se décharge et qu'entre 8 s et 9 s il se recharge dans le sens inverse.
Intervalle de 9 à 13 secondes. La tension augmente uniformément de -30 à +10V, ce qui représente une variation de +40V.
On trouve:
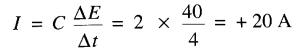
La pente de la tension étant positive, le courant est également positif.
Intervalle de 13 à 14 secondes. La tension ne varie pas: le courant est donc nul. On observe, pour chacun de ces intervalles, que le sens du courant ne dépend pas de la polarité de la tension mais seulement de son taux de variation.
Enfin, on constate que la forme d'onde du courant diffère totalement de celle de la tension.
Applications des condensateurs
En électrotechnique, les condensateurs sont surtout utilisés
a) pour la correction du facteur de puissance
b) pour le démarrage des moteurs monophasés
c) pour réaliser des filtres
d) pour régulariser la tension sur les lignes à courant alternatif
e) pour la suppression des arcs
f) pour faire des oscillateurs
Condensateurs fonctionnant à courant alternatif
La plupart des condensateurs industriels sont des appareils monophasés installés sur les réseaux à courant alternatif, fonctionnant à 60 Hz. Leur capacité varie de 5 kvar à 200 kvar et leur tension nominale est comprise entre 240 V et 14,4 kV.
Quand il faut réaliser des installations de grande puissance, on groupe les condensateurs en série, en parallèle et en série-parallèle, selon la tension du réseau.
Leur puissance massique et volumique, à 60 Hz, atteint respectivement des valeurs aussi élevées que 4 kvar/kg et 7 kvar/dm³.
Le champ électrique alternatif entre les plaques du condensateur produit des pertes diélectriques qui sont dégagées sous forme de chaleur.
Selon les normes, la puissance dissipée doit être inférieure à 3 1/3 W par kvar pour des condensateurs fonctionnant à 60 Hz. Les pertes sont proportionnelles à la fréquence mais elles parient avec le carré de la tension appliquée; on doit donc éviter d'appliquer une tension supérieure à 110 % de la tension nominale.
Afin d'assurer une durée de vie raisonnable, l'augmentation de la température à la surface du boîtier ne doit pas dépasser 25 °C.
Pour les applications spéciales à haute fréquence (1 kHz à 10 kHz), on refroidit les condensateurs en faisant circuler de l'eau dans des tubes entourant le boîtier.
Les puissances, les tensions et la performance en général des condensateurs doivent se conformer aux standards établis par les bureaux de normalisation.
En voici quelques exemples:
1. Normes de surtension: un condensateur monophasé doit pouvoir supporter pendant au moins 10 secondes une tension alternative valant le double de la tension nominale.
2. Normes pour la tension de tenue aux ondes de choc: un condensateur monophasé doit pouvoir résister aux ondes de choc données au tableau 21-4.
Noter que l'onde de choc est appliquée entre les bornes en court-circuit et le boîtier du condensateur.
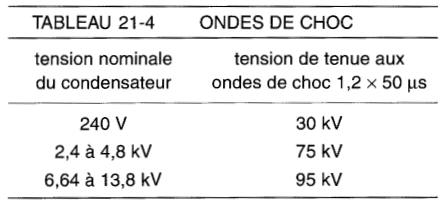
3. Normes de sécurité: la tension résiduelle aux bornes d'un condensateur de 600V et moins doit être inférieure à 50V une minute après que la source a été débranchée. Pour des tensions supérieures à 600V, on permet un délai de 5 minutes. C'est pourquoi le fabricant incorpore souvent une résistance de décharge à l'intérieur même du boîtier.
Il est toujours prudent de court-circuiter les bornes d'un condensateur avant d'y toucher. S'il peut emmagasiner une énergie supérieure à 10 J, il est préférable de le décharger au moyen d'une résistance avant d'appliquer le court-circuit.
En effet, une énergie de 10 J dissipée en une fraction de milliseconde peut produire un arc destructif. Lorsque les normes sont respectées, et dans les conditions environnantes appropriées, un condensateur peut atteindre une durée de vie de 20 à 50 ans. Cependant, comme tout appareil électrique, on doit le protéger par des fusibles.
FORMULES POUR CALCUL DE CAPACITANCES
Le calcul de la capacitance de certaines formes de conducteurs est particulièrement utile. Les sections qui suivent en donnent quelques exemples.
Capacitance de deux fils parallèles
Deux fils conducteurs parallèles (Fig . 21-18)
Figure 21-18 Capacitance de deux fils parallèles
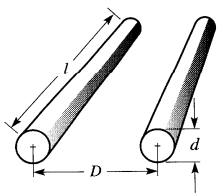
forment un condensateur dont la capacitance est donnée par la formule:
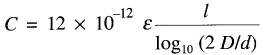(21-7)
où
C = capacitance de la
ligne [F]
e = constante diélectrique de l'isolant séparant les conducteurs
l = longueur de chaque conducteur [m]
D = distance séparant les conducteurs [m]
d = diamètre du conducteur [m]
12 x 10-12 = facteur tenant compte des unités
La précision de cette formule est plus petite que 2 % si le rapport D/d est plus grand que 3.
Exemple 21-5
Calculer la capacitance d'une ligne à haute tension de 12 km formée de 2 conducteurs ayant un diamètre de 16 mm et espacés de 3,2 m.
Solution
La capacitance est:
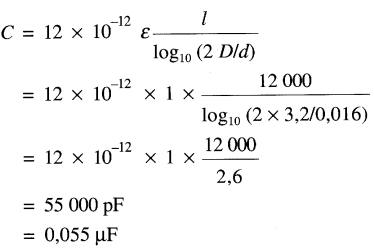
Capacitance d'un câble coaxial La capacitance d'un câble coaxial (Fig. 21-19)
Figure 21-19 Capacitance d'un câble coaxial
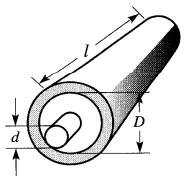
est donnée par l'équation:
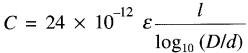(21-8)
où
C = capacitance du
câble [F]
ε = constante diélectrique de l'isolant séparant les conducteurs
l = longueur du câble [m]
D = diamètre intérieur du conducteur extérieur [m]
d = diamètre du conducteur intérieur [m]
24 x 10-12 = facteur tenant compte des unités.
Cette formule s'applique pour toute valeur de D et d.
Exemple 21-6
Trouver la capacitance d'un câble sous-marin long de 17 km et dont les diamètres sont :
D = 48 mm et d = 28 mm (prendre ε = 3,6).
Solution
D'après l'équation, on a:
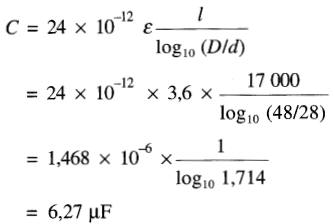
Capacitance d'une sphère par rapport à une surface plane
La capacitance formée par une sphère métallique et une grande surface plane conductrice (la terre, par exemple) est donnée par l'équation :
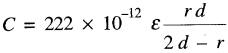(21-9)
où
C = capacitance [F]
ε = constante diélectrique de l'isolant entre la sphère et la surface
d = distance entre le centre de la sphère et la surface [m]
r = rayon de la sphère [m]
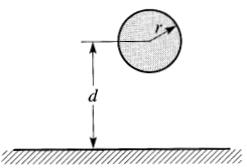
Cette équation est toujours valable lorsque d est plus grand que r (Fig. 21-20).
Figure 21-20 Capacitance entre une sphère et une surface plane
Si la sphère est éloignée d'une grande distance de la surface, la capacitance tend vers la valeur:
C = 111 x 10-12 εr (21-10)
On l'appelle parfois, à tort, «capacitance de la sphère», comme si la sphère possédait une capacitance en soi. Cette interprétation est incorrecte car il faut toujours deux corps pour former un condensateur.
Résumé
Dans cette section, nous avons introduit un nouvel élément : le condensateur et la grandeur qui le caractérise: la capacitance.
La capacitance est le rapport entre la quantité d'électricité transférée d'une des plaques du condensateur à l'autre et la tension appliquée entre ses bornes. L'unité SI de capacitance est le farad (F).
On emploie plus souvent ses sous-multiples (microfarad, µF; nanofarad, nF; picofarad, pF). La valeur de la capacitance dépend de la forme des plaques, de leurs dimensions et de la constante diélectrique de l'isolant qui les sépare.
Différents types de diélectriques sont disponibles . Nous savons comment calculer la capacitance d'un groupement de condensateurs en série ou en parallèle.
Un condensateur chargé conserve dans le champ électrique de son diélectrique une énergie qui dépend de sa capacitance et de sa tension de charge.
Lorsqu'une tension continue est appliquée à un condensateur C en série avec une résistance R, le condensateur se charge et la tension entre ses bornes augmente en fonction du temps selon une courbe exponentielle.
Le temps requis pour que la tension du condensateur atteigne la tension de source dépend de la constante de temps τ = RC.
De la même façon que pour le circuit inductif L-R, on peut utiliser le demi-temps T0 et un tableau universel pour tracer facilement les courbes exponentielles de charge et de décharge.
Plus généralement, lorsque la tension aux bornes d'un condensateur varie de façon quelconque, le courant circulant dans le condensateur dépend du taux de changement ΔE/Δt de la tension. Le courant I est donné par la loi fondamentale I = C ΔE/Δt.
Lorsque la tension augmente, le condensateur se charge et le courant entre par la borne positive du condensateur.
De la même façon qu'une bobine s'oppose au changement rapide du courant qui la traverse, on peut dire qu'un condensateur « s'oppose » à un changement de tension rapide entre ses bornes car il doit accumuler une certaine charge pour que la tension change.
Pour cette raison, les condensateurs sont parfois utilisés comme méthode de protection contre les surtensions momentanées. P
PROBLÈMES
21-1 Nommer l'unité SI de capacitance et donner deux sous-multiples.
21-2 Quel genre de condensateur emmagasine la plus grande quantité d'énergie par rapport à ses dimensions?
21-3 Pourquoi doit-on brancher une résistance en parallèle avec les bornes d'un condensateur industriel?
21-4 Expliquer pourquoi un condensateur se décharge très rapidement à travers une faible résistance.
21-5 Une source spéciale fournit un courant constant de 1 mA à un condensateur de 50 µF. En combien de temps la tension atteindra-t-elle 500 volts?
21-6 Un condensateur de 100 µF porte une charge de 0,004 coulomb. Calculer la tension à ses bornes.
21-7 Un condensateur de 10 µF, 1 kV est plus petit qu'un autre de 10 µF, 10 kV. Expliquer.
Niveau intermédiaire
21-8 Les plaques d'un condensateur ont une surface de 2m².
a) Calculer la capacitance sachant qu'elles sont séparées par une feuille de papier dont l'épaisseur est de 0,5 mm (consulter le tableau 21-1);
b) Quelle aurait été la capacitance si on avait employé du mica au lieu du papier?
21-9 Deux condensateurs de 5 µF et de 20 µF sont reliés en série à une source de 1000 V.
Calculer:
a) la capacitance totale
b) la tension aux bornes de chacun des condensateurs
21-10 La tension aux bornes d'un condensateur de 10 µF change de +60V à +300V en 1 ms.
Calculer la valeur du courant. Le condensateur se charge-t-il?
21-11 Soit 3 condensateurs de 42 µF, 30 µF et 7 µF ayant chacun une tension nominale de 600V.
Calculer:
a) la capacitance totale du groupe si on les branche en série
b) la capacitance totale du groupe si on les branche en parallèle
c) la tension maximale que l'on peut appliquer sur le groupe dans chaque cas sans risquer le claquage
21-12 Calculer l'énergie volumique du condensateur (f) de la Fig. 21-9.
21-13 Un accumulateur d'automobile de 12V peut débiter un courant de 15A pendant 2 heures. Combien de condensateurs du type (c) (Fig . 21-9) sont-ils requis pour fournir la même quantité d'énergie?
21-14 Cinquante condensateurs de 30 µF sont raccordés en parallèle sur une source de 2 kV. Si l'isolant se rompt à l'intérieur d'un des condensateurs, l'unité en défaut risque d'exploser. Expliquer.
Quelle précaution doit-on prendre pour éviter ce problème?
21-15 Un condensateur de 500µF, chargé à une tension de 600V, se décharge complètement dans une résistance de 1,2 MΩ.
Calculer:
a) la constante de temps du circuit
b) la durée du «demi-temps»
c) l'énergie dissipée en chaleur durant la décharge
Niveau avancé
21-16 Deux condensateurs de même capacitance fa- briqués avec le même type de diélectrique sont isolés pour des tensions respectives de 600V et 4800V.
Montrer que le deuxième condensateur aura un volume de diélectrique 64 fois plus grand que le premier. Quel est le rapport entre les énergies emmagasinées dans chacun des deux condensateurs lorsqu'ils fonctionnent à leur tension nominale?
21-17 Cent feuilles de 0,8 m x 2,5 m en aluminium ayant une épaisseur de 0,05 mm sont intercalées avec 99 plaques de verre ayant une épaisseur de 1,6 mm.
Cinquante feuilles sont connectées ensemble pour former un pôle du condensateur; les 50 autres feuilles forment le deuxième pôle.
Sachant que le verre a une constante diélectrique de 6 et une rigidité diélectrique de 50 kV/mm, calculer:
a) la capacitance du condensateur
b) la tension maximale qu'on peut lui appliquer, et l'énergie emmagasinée
21-18 Dans le problème 21-17, les plaques de verre doivent être plus grandes que les feuilles en aluminium. Quelles doivent être les dimensions minimales des plaques de verre, étant donné que la rigidité diélectrique de l'air est de 3 kV/mm?
21-19 Un condensateur de 3 µF fonctionne à une tension nominale de 20 kV. Il doit se décharger à une tension de 50V en moins de 5 min .
Trouver:
a) la valeur approximative de la résistance de décharge requise
b) la puissance dissipée dans celle-ci en régime permanent
21-20 Lors du passage d'une onde de choc, on constate que la tension aux bornes d'un condensateur de 0.2 µF a augmenté de 150 V (Fig. 21-16). Quelle charge a été absorbée par le condensateur?
21-21 Les deux sphères de la Fig . 20-3a possèdent une capacitance de 400 pF et la d.d.p. est de 60 kV. Lorsqu'on les sépare (Fig. 20-3b), on constate que la capacitance diminue à 300 pF.
Calculer:
a) la tension entre les sphères lorsqu'elles sont séparées
b) l'énergie mécanique qu'on a dû fournir pour séparer les sphères
21-22 Calculer la capacitance entre deux fils nus #4 espacés de 0,5 m et ayant une longueur de 10 km.
21-23 Le câble montré à la Fig. 10-12c possède un conducteur intérieur et une gaine de plomb métallique extérieure (anneau noir).
Mesurer les dimensions du câble avec une règle. Calculer la capacitance de 10 km de ce câble sachant que l'isolant possède une constante diélectrique de 3.
5) 25 s; 6) 40 V; 8a) 88,5 nF;
8b) 248 nF; 9a) 4 µF;
9b) 800V; 200V; 10) 2,4A; oui; 11 a) 5µF; 11 b) 79µF;
11 c) série: 840V; parallèle: 600V; 12) 56,9 kJ/m³; 13)144000;
5a) 600 s;
15b) 420 s; 15c) 90 J; 16)64; 17a) 6,57µF;
17b) 80 kV; 24,5 kJ; 18) 0,825 x
2,525 m ; 19a) 16,7 MΩ;
19b) 25 W; 20) 30 µC; 21a) 80 kV; 21b) 0,24 J;
22) 52,5 nF;
23)-1,8µF
