Circuits magnétiques
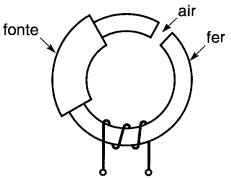
Un circuit électrique est composé d'un ensemble d'éléments reliés les uns aux autres et destinés à conduire un courant électrique. De façon analogue, un circuit magnétique est composé d'un groupe de corps reliés les uns aux autres et destinés à conduire un flux magnétique (Fig. 14-1).
Figure 14-1 Exemple de circuit magnétique

Dans cette section, nous étudions les circuits magnétiques. Nous verrons qu'ils ressemblent aux circuits électriques étudiés à la section Circuits simples à courant continu.
Ainsi, on retrouve des Figure 14-1 circuits magnétiques en série, en parallèle et en série-parallèle.
Champ magnétique à l'intérieur d'un tore
L'exemple suivant servira à illustrer quelques-unes des propriétés des circuits magnétiques. Plions un tube de caoutchouc en forme de U et bobinons sur ce tube des spires espacées régulièrement (Fig. 14-2a).
Figure 14-2
a. La bobine produit un flux et deux pôles, N et S.
b. Lorsque la bobine est refermée sur elle-même, le flux demeure, mais les pôles N,S disparaissent

Supposons que le sens du courant dans la bobine soit tel que les lignes de force aient le sens indiqué, avec la polarité magnétique nord-sud correspondante.
Si maintenant on joint les deux bouts du tube de caoutchouc de façon à former un anneau de section circulaire, appelé tore, les pôles nord et sud disparaissent et les lignes de force restent à l'intérieur de la bobine et se referment sur elles-mêmes (Fig. 14-2b). Ce montage constitue un solénoïde toroidal.
Nous allons maintenant étudier dans ce circuit magnétique, l'effet (1) de la longueur du chemin magnétique, (2) de sa section et (3) de la nature du matériau constituant le tore.
Pour fins de simplification, et comme point de départ, prenons l'exemple numérique du tore de la Fig. 14-3.
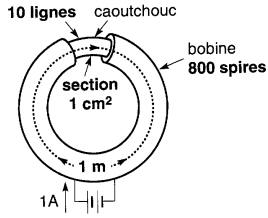
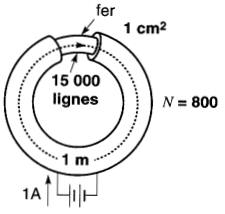
Figure 14-3 Données du tore servant à analyser les propriétés d'un circuit magnétique
Ses données sont:
Données du solénoïde
toroïdale
Section du noyau de caoutchouc : 1 cm²
Longueur moyenne du chemin magnétique: 1 m
Courant dans la bobine: 1A
Nombre de spires de la bobine : 800
Nombre de lignes à l'intérieur du tore : 10
La force magnétomotrice de la bobine vaut: FMM = 1 A x 800 spires = 800 ampères ou 800 ampères-tours Apportons des changements successifs à ce tore afin de constater l'effet sur le flux.
1. Effet de la longueur du chemin magnétique
Le tore de la Fig. 14-4a est identique à celui de la Fig. 14-3, à l'exception de la longueur qui a été augmentée de 1 mètre à 2 mètres.
Figure 14-4a Lorsque la longueur du chemin magnétique double, le flux diminue de moitié
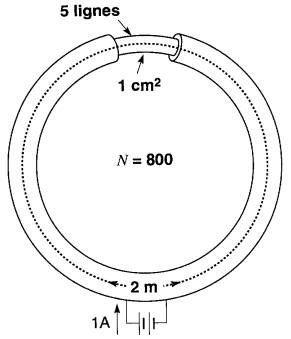
Les 800 spires de la bobine sont enroulées uniformément sur sa longueur. On constate alors que le nombre de lignes de force à l'intérieur de la bobine a diminué de moitié.
Donc une même force magnétomotrice de 800 ampères ne produit plus que 5 lignes.
De façon très intuitive, on peut dire qu'en doublant la longueur du chemin magnétique, on double la «résistance» au passage des lignes de force.
Ceci est analogue au passage du courant dans un circuit électrique: en doublant la longueur du conducteur, on double sa résistance.
Dans un circuit magnétique, l'opposition au passage des lignes de force est appelée réluctance. On constate que la réluctance est proportionnelle à la longueur du chemin magnétique.
2. Effet de la section du chemin magnétique
Le tore de la Fig. 14-4b est identique à celui de la Fig. 14-3 à l'exception de la section du tube de caoutchouc qui, cette fois-ci, est augmentée à 2 cm2.
Figure 14-4b Lorsque la section du chemin magnétique double, le flux double
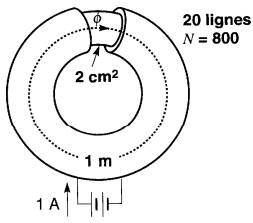
On découvre que pour une même force magnétomotrice de 800 A, on obtient alors un flux de 20 lignes.
En doublant la section du chemin magnétique, l'opposition (ou réluctance) au passage des lignes de flux diminue de moitié. Donc, on constate que la réluctance du chemin magnétique est inversement proportionnelle à la section.
3. Effet de la nature du noyau
Si le noyau de caoutchouc du solénoïde est remplacé par un noyau de bois ou de tout autre matériau non magnétique, le nombre de lignes de force ne changera pas à l'intérieur de la bobine.
Si, par contre, on remplace le noyau par un noyau de fer, de cobalt, de nickel ou d'un alliage de ces matériaux magnétiques, le nombre de lignes sera considérablement augmenté.
Ainsi, le flux à l'intérieur de la bobine de la Fig. 14-4c peut devenir plusieurs centaines de fois plus grand en remplaçant le noyau de caoutchouc par un noyau de fer doux!
Figure 14-4c Lorsque le noyau de caoutchouc est remplacé par un noyau de fer, le flux augmente des centaines de fois.
On en conclut que les matériaux magnétiques facilitent grandement le passage des lignes de force.
La réluctance d'un circuit magnétique est donc réduite de beaucoup par l'emploi d'un matériau magnétique.
En résumé, la réluctance d'un circuit magnétique dépend de sa longueur, de sa section et du matériau dont il est constitué.
Perméabilité magnétique
Comme nous l'avons vu tout se passe comme si les matériaux magnétiques étaient très perméables aux lignes de force, d'où le nom de perméabilité pour caractériser la facilité avec laquelle ces matériaux se laissent traverser par les lignes.
Les matériaux magnétiques ne sont pas tous aussi perméables les uns que les autres : la fonte n'est pas aussi perméable que le fer doux, son opposition (ou réluctance) au passage des lignes de force sera donc plus grande.
On dit alors que la perméabilité du fer doux est supérieure à celle de la fonte.
Explication de la perméabilité
Considérons de nouveau deux bobines toroïdales (Fig. 14-5), identiques à celle de la Fig. 14-3, dont les 800 spires portent le même courant de 1 ampère.
Figure 14-5 Notion de perméabilité d'un matériau magnétique :
a. Le solénoïde à noyau non magnétique produit 10 lignes de flux;
b. Le solénoïde à noyau de fer produit 15 000 lignes
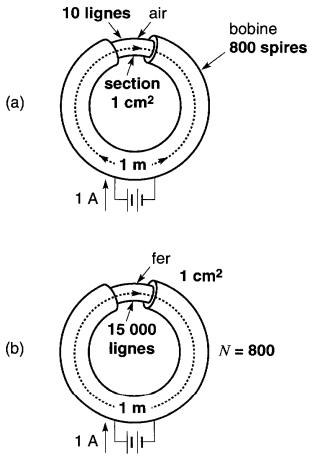
Le noyau du tore de la Fig. 14-5a est constitué d'un matériau non magnétique comme l'air, tandis que celui de la Fig. 14-5b est en fer doux. Comme les bobines ont le même nombre de spires et portent le même courant, elles produisent la même FMM.
Cependant, si l'on pouvait mesurer au moyen d'un «fluxmètre» le nombre de lignes traversant chacun des noyaux, on constaterait que le nombre de lignes dans le fer doux dépasse des centaines de fois celui dans l'air.
Par exemple, on peut obtenir une va.leur de 15 000 lignes pour le fer doux et une valeur de 10 lignes seulement pour l'air. On peut expliquer ce résultat en considérant la théorie des domaines magnétiques.
Tout d'abord, remarquons que pour une même FMM de 800 A, la bobine produit toujours 10 lignes, que le noyau soit composé d'un matériau magnétique ou non.
Cependant, dans le cas du noyau de fer (Fig.14-5b), les lignes de force de la bobine agissent sur les domaines magnétiques et tendent à les orienter dans une même direction. Ces domaines créent donc des lignes de force additionnelles qui s'ajoutent aux 10 lignes engendrées par la bobine.
Ainsi, à la Fig. 14-5b, le flux total de 15 000 lignes est composé de 10 lignes produites par la bobine même et de 14 990 lignes créées par les domaines magnétiques.
Perméabilité relative
Le rapport entre le nombre total des lignes de force (ou flux magnétique) dans un matériau et celui dans l'air est appelé perméabilité relative (µr) du matériau.
µr = flux dans le matériau / flux dans l'air (14-2)
En fait, la perméabilité relative se définit par rapport au vide. Mais comme la perméabilité du vide est sensiblement égale à celle de l'air, l'équation 14-2 est assez précise pour nos besoins. (µ est une lettre grecque qui se prononce «mu».)
Dans l'exemple précédent (Fig. 14-5), la perméabilité relative du fer doux est:
µr = 15 000 / 10 = 1500
Dans cet exemple, l'opposition du fer doux au passage des lignes de force est donc 1500 fois plus faible que celle de l'air.
Certains alliages spéciaux, tels que le Permalloy, ont des perméabilités relatives qui atteignent des valeurs de l'ordre de 1 000 000.
La perméabilité d'un matériau magnétique (comme le fer) n'est pas constante ; elle varie avec la densité de flux magnétique. Ceci provient du fait que l'augmentation du flux dans le matériau magnétique n'est pas proportionnelle à l'augmentation de la FMM qu'on lui applique.
Ce fait est mis en évidence à la section suivante.
Courbe de saturation du fer
Considérons de nouveau le solénoïde toroïdal de la Fig. 14-3 dont la longueur moyenne du chemin magnétique est de 1 mètre, et la section de 1 cm².
On a vu que lorsque le noyau du tore est constitué de caoutchouc ou d'un autre matériau non magnétique, une force magnétomotrice de 800 ampères y fait circuler un flux de 10 lignes.
Si on augmente la FMM graduellement, on observe que le flux augmente en proportion. Par exemple, lorsque la FMM est doublée à 1600 A, le flux sera de 20 lignes.
Si l'on porte sur un graphique les valeurs correspondantes de la force magnétomotrice et du flux (Fig. 14-7), on constate qu'elles peuvent être jointes par une ligne droite, soit la courbe (a).
Figure 14-7 Courbe de saturation pour un matériau non magnétique (a) et pour le fer (b)
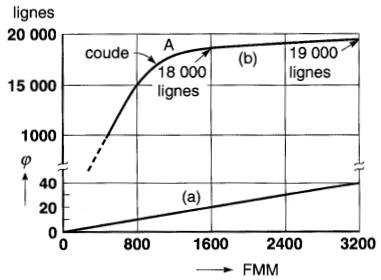
On vérifiera sur cette droite qu'un flux de 40 lignes dans le noyau correspond à une FMM de 3200 A. Le flux dans un matériau non magnétique est donc proportionnel à la FMM.
Remplaçons maintenant le noyau de caoutchouc par un noyau de fer, et faisons croître graduellement la FMM de 0 à 3200 A, en notant les valeurs correspondantes du flux magnétique.
Si l'on trace un nouveau graphique donnant la relation entre la FMM et le flux, on n'obtient plus une droite mais une courbe (b) qu'on appelle courbe de saturation (Fig. 14-7).
Jusqu'au point A (appelé «coude» de la courbe) le flux croît très rapidement avec l'augmentation de la force magnétomotrice.
Passé ce point, le nombre de lignes croît assez peu, même pour une grande augmentation de la force magnétomotrice. Ainsi, dans l'exemple ci.dessus, pour une FMM de 800 A, le flux est de 15 000 lignes; pour une FMM de 1600 A, il est de 18 000 lignes seulement.
Enfin, en doublant de nouveau la FMM à 3200 A, le nombre de lignes n'augmente que de 1000, pour donner 19 000 lignes.
Ceci provient du fait que lorsque le noyau de fer est soumis à une FMM relativement faible, une partie importante des milliers de domaines s'alignent avec ce champ.
Leur contribution au flux est énorme, de sorte que le flux augmente très rapidement avec la FMM. Au fur et à mesure que la FMM augmente, un plus grand nombre de domaines s'orientent dans le sens du champ, et le nombre de lignes continue à croître.
En augmentant la FMM davantage, on finit par atteindre la condition où tous les domaines sont alignés. Par conséquent, même si l'on persiste à augmenter la FMM, les domaines ne créent plus de lignes supplémentaires.
On dit alors que le fer est saturé. La saturation du fer correspond à la condition montrée à la Fig. 12-16c, section Magnétisme.
Lorsque le fer est saturé, le flux continue à augmenter avec la FMM. Cette croissance correspond aux lignes magnétiques créées dans un matériau vide, comme de l'air.
On remarque sur la Fig. 14-7 qu'une FMM de 800 A donne une perméabilité relative de:
µr = 15 000 lignes / 10 lignes = 1500
tandis qu'une FMM de 3200 A donne une perméabilité relative de seulement:
µr = 19 000 lignes / 40 lignes = 475
On peut tirer une conclusion importante de ce phénomène: passé le point de saturation, il est rarement recommandable de faire une dépense supplémentaire de cuivre ou de courant pour augmenter la FMM d'une bobine, car l'augmentation de flux ainsi obtenue n'est plus assez forte.
Densité de flux (B)
Le flux θ (en webers) qui traverse un échantillon ferromagnétique ne révèle pas s'il est saturé ou non.
Cependant, connaissant la densité de flux (en teslas), il est facile d'établir le degré de saturation de l'échantillon, à l'aide de tables ou de courbes fournies pour tous les matériaux magnétiques usuels.
Si l'on connaît le flux qui traverse une surface perpendiculaire à la direction du flux, on peut évaluer la densité de flux.
Par définition, la densité de flux B traversant une surface A est donnée par la formule :
B = θ / A (14-3)
où
B = densité de flux,
en teslas [T]
θ = flux traversant la surface, en webers [Wb]
A = surface, en
mètres carrés [m²]
Exemple 14-1
Le circuit magnétique d'un transformateur est composé d'un ensemble de tôles d'acier superposées (Fi-. 14-8). La section du noyau magnétique est égale à 4 cm x 5 cm.
Figure 14-8 Voir exemple 14-1
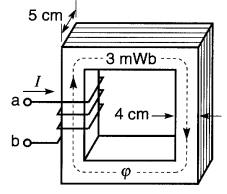
Sachant que le flux traversant ce noyau est de 3 mWb, trouver la densité de flux dans l'acier.
Solution
La section du noyau vaut:
A = 4 cm x 5 cm = 4/100 x 5/100 = 0,002 m²
θ = 3 mWb = 0,003 Wb
d'où
B = θ / A = 0.003 / 0.002 = 1,5 teslas = 1,5 T
Champ magnétique (H)
Le champ magnétique (symbole H) en un point est la force magnétomotrice exercée par unité de longueur. Dans le SI, elle est exprimée en ampères par mètre [A/m].
Le tore homogène de la Fig. 14-9 possède une longueur de 1 mètres et la FMM qui agit sur tout le circuit est de NI ampères.
Figure 14-9 Champ magnétique à l'intérieur d'un tore: H = Nul
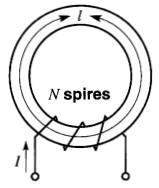
Par définition, le champ magnétique (H) à l'intérieur du tore vaut Nul ampères par mètre. On doit noter que le terme champ magnétique a deux significations: il désigne soit une région contenant des lignes de force, soit une grandeur précise mesurée en A/m.
Dans le SI, le champ magnétique est exprimé en ampères par mètre, et non en ampères-tours par mètre, le mot «tour» étant sous-entendu.
Exemple 14-2
Une pièce de matériau homogène et de section constante a une longueur de 0.3 mètre.
Si elle est soumise à une FMM de 720 ampères, quel est le champ magnétique?
Solution
Le champ magnétique est:
H = 720A / 0.3 m = 2400 A/m
Courbe d'aimantation B-H du vide
Pour un échantillon donné de matériau magnétique, il existe une relation bien définie entre la densité de flux (B) et le champ magnétique (H) qui la produit. Il est bon de se rappeler que dans un circuit magnétique c'est le champ magnétique H qui donne naissance au flux. Cette relation est exprimée graphiquement par la courbe d'aimantation B-H du matériau.
Quelle est la nature de cette relation dans le cas du vide?
Dans le vide, la densité de flux B est exactement proportionnelle au champ magnétique H.
C'est ce qu'exprime la relation:
B = µo H (14-4)
ou
B = densité de flux,
en teslas [T]
H = champ magnétique, en ampères par mètre [A/m]
µo = constante, appelée constante magnétique ou perméabilité du vide = 4π x 10-7 (= 1/800 000 environ)
Dans le SI, la constante magnétique µo est fixée par définition à une valeur numérique de 4π x 10-7 ou 1/800 000 environ.
L'expression complète de µo est 4π x 10-7 henry/mètre.
Cela nous permet d'écrire l'équation 14-4 sous la forme approximative :
B = H / 800 000 (14-5)
La courbe d'aimantation du vide est donc une ligne droite qui ne révèle aucune saturation, quelle que soit la grandeur de B ou de H(Fig. 14-11). On vérifiera sur cette courbe qu'un champ de 8000 A/m produit, dans le vide, une densité de flux de 10 milliteslas.
Figure 14-11 Courbe d'aimantation du vide et des matériaux non magnétiques
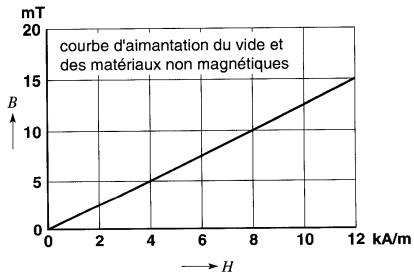
Les matériaux non magnétiques ont tous une perméabilité relative sensiblement égale à 1, de sorte que leurs courbes d'aimantation sont presque identiques à celle du vide.
L'air, par exemple, possède une perméabilité relative de 1,000 000 4, ce qui indique qu'il est à peine plus perméable que le vide.
Courbe d'aimantation B-H d'un matériau magnétique
La densité de flux B dans un matériau magnétique dépend aussi du champ magnétique H; sa valeur est donnée par l'équation:
B = µoµrH (14-6)
où
B, µo et H ont la même signification qu'auparavant et µr représente la perméabilité relative du matériau.
Malheureusement, la valeur de la perméabilité relative µr n'est pas constante, mais dépend de la densité de flux dans le matériau. Il s'ensuit que la relation entre B et H n'est pas linéaire, ce qui rend l'équation 14-6 peu utile.
Pour ces matériaux, on est donc obligé de représenter la relation entre la densité B et le champ H par une courbe d'aimantation.
La Fig. 14-12 donne les courbes d'aimantation de trois matériaux employés dans les machines électriques: acier au silicium (1 %), fonte et acier coulé. On vérifiera sur ces courbes qu'un champ magnétique de 2000 A/m produit des densités de flux de 1,4 T pour l'acier coulé et 0,5 T pour la fonte.
Fig. 14-12 Courbe d'aimantation de trois matériaux magnétiques
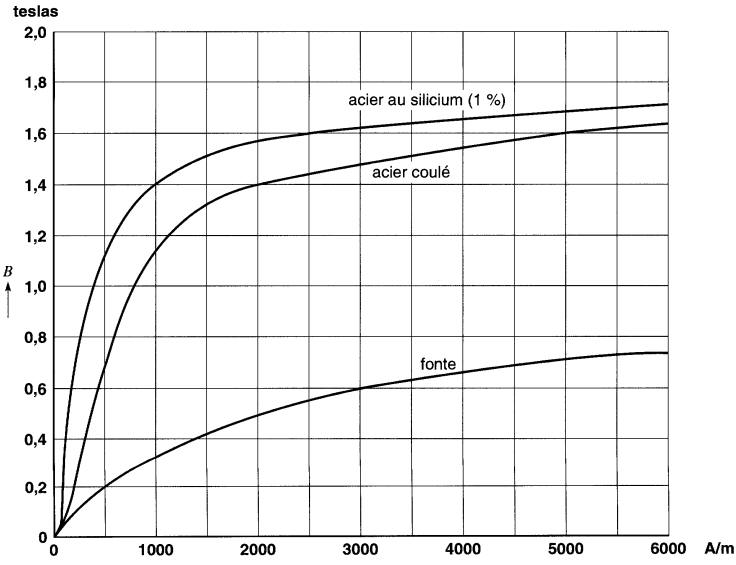
La Fig. 14-13 donne les courbes d'alimentation de quelques matériaux magnétiques, étendues sur une grande échelle de H.
On remarque que toutes les courbes tendent finalement vers la courbe d'aimantation du vide lorsque le champ magnétique H est suffisamment intense. Cette courbe passe par les points (0,1 T, 80 000 A/m) et (1,25 T, 106 A/m). 1
Détermination de la perméabilité relative
Lorsqu'on connaît la courbe d'aimantation d'un matériau magnétique, il est facile d'en déduire la perméabilité relative en un point quelconque. Grace à l'équation 14-6, on obtient l'expression approximative :
µr = 800 000 B / H (14-7)
où
µr = perméabilité relative [un nombre]
B = densité de flux
dans le matériau [T]
H = champ magnétique agissant sur le
matériau [A/m]
800 000 = constante [valeur exacte = 107/4π]
Exemple 14-3
Qu'elle est la perméabilité de l'acier au silicium (1%) lorsqu'il est utilisé à une densité de 1.4 T?
Solution
En se reportant à la courbe d'aimantation de la Fig. 14-12, on constate que pour l'acier au silicium, la valeur de H correspondant à 1,4 T est de 1000 A/m.
Il s'ensuit que µr = 800 000 B / H
= 800 000 x 1,4 / 1000 = 1120
À cette densité de flux, l'acier est donc 1120 fois plus perméable que le vide.
Exemple 14-4
En se reportant à la Fig. 14-13 déterminer la perméabilité relative du nickel à une densité de 0,6T.
Figure 14-13 Courbes d'aimantation permettant une comparaison entre les matériaux magnétiques et non magnétiques. Noter que toutes les courbes deviennent asymptotiques à la courbe B-H du vide lorsque le champ magnétique H est suffisamment intense.
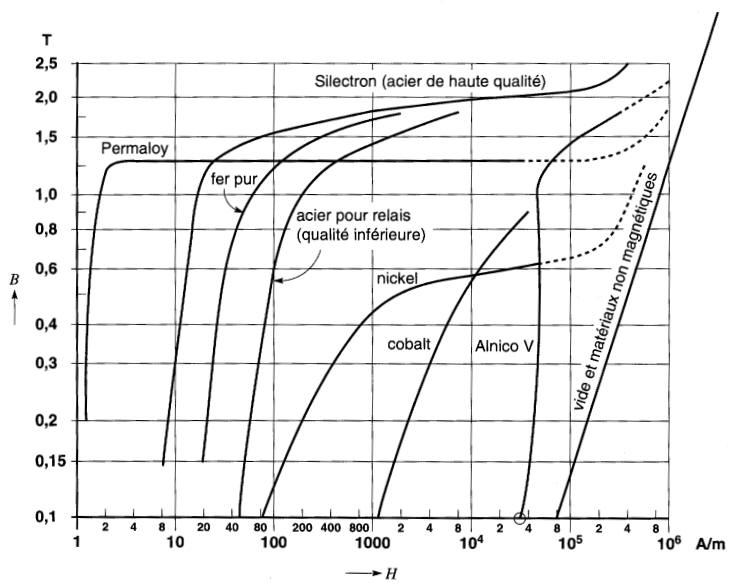
Solution
Pour obtenir une densité de flux de 0,6 T, la courbe d'aimantation indique un champ magnétique H de 3 x 104 A/m.
Par conséquent:
µr = 800 000 B / H
donc
µr = 800 000 x 0,6 / 30 000 = 16
Analogie entre circuits électriques et circuits magnétiques
Si l'on établit un parallèle entre les circuits électriques et les circuits magnétiques, on s'aperçoit qu'il existe une grande analogie entre:
1. le courant électrique I et le flux magnétique θ
2. la différence de potentiel E et la force magnétomotrice FMM
3. la résistance R et la réluctance R
4. la résistivité p et l'inverse de la perméabilité 1/µ
Les lignes de flux qui se referment sur elles-mêmes dans les circuits magnétiques sont analogues aux courants électriques.
La force magnétomotrice peut être considérée comme une différence de potentiel magnétique qui, appliquée entre deux points d'un circuit magnétique, fera circuler des lignes de flux entre ces points.
La FMM d'une bobine est donc comparable à la force électromotrice d'une génératrice électrique.
Enfin, l'opposition au passage des lignes de flux, ou réluctance d'un chemin magnétique, est analogue à la résistance électrique d'un conducteur.
À l'expression de la loi d'Ohm
I = E / R
correspond la relation:
θ = FMM / R
où
θ = flux dans le circuit magnétique [Wb]
FMM = force
magnétomotrice agissant sur le circuit magnétique [A]
R =
réluctance du circuit magnétique [A/Wb]
Il existe cependant des différences importantes entre les circuits électriques et les circuits magnétiques :
1. l'air, parfait isolant électrique, peut être traversé par des lignes de force et fait souvent partie de circuits magnétiques;
2. le courant électrique correspond à un mouvement d'électrons tandis que la «circulation» du flux ne correspond à aucun mouvement;
3. la conductivité de la plupart des matériaux conducteurs est assez constante, alors que la perméabilité des matériaux magnétiques varie avec le flux qui les traverse. À cause de cette non-linéarité, il est plus difficile de résoudre les circuits magnétiques que les circuits électriques.
En effet, pour résoudre les circuits magnétiques, on est obligé d'utiliser les courbes d'aimantation B-H; si les matériaux magnétiques avaient des perméabilités constantes, on pourrait résoudre les circuits magnétiques avec autant de facilité que l'on résout les circuits électriques.
Solution des circuits magnétiques simples
En pratique, pour les circuits magnétiques, on a à résoudre l'un ou l'autre des deux problèmes suivants :
1. Calculer la FMM nécessaire pour obtenir un flux déterminé dans un circuit magnétique connu.
2. Pour une FMM donnée, évaluer le flux produit dans un circuit magnétique connu.
On rencontre souvent des entrefers dans les machines et les dispositifs électriques.
Par conséquent, il est utile de connaître la FMM requise pour produire un flux quelconque dans un entrefer.
L'équation 14-5 nous permet de calculer la FMM requise pour forcer un flux de densité B à travers un entrefer de longueur
1. En effet,
B = H / 800 000 = FMM / 800 000 l
d'où
FMM = 800 000 Bl
(14-9)
où
FMM = force magnétomotrice requise [A]
B = densité
de flux dans l'entrefer [T]
l = longueur de l'entrefer [m]
Exemple 14-5
FMM réguise pour un entrefer.
On désire produire une densité de flux de 0.7 tesla dans un entrefer dont la longueur est de 2 millimètres (Fig. 14-14).
Figure 14-14 Voir exemple 14-5
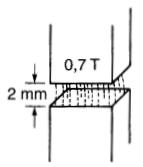
Calculer la FMM requise.
Solution
D'après l'équation (14-9) la FMM requise est:
FMM = 800 000 Bl = 800 000 x 0,7 x (2 / 1000) = 1120A
Exemple 14-6
FMM requise pour le fer.
Soit le noyau d' un transformateur composé de tôles d'acier au silicium (1 %). Les dimensions du noyau sont données à la Fig. 14-15.
Figure 14-15 Voir exemple 14-6
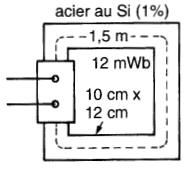
La longueur moyenne de son chemin magnétique est de 1,5 mètres. Quelle doit être la force magnétomotrice de la bobine qui produira un flux de 12 mWb dans ce noyau?
Solution
On pourrait faire le calcul en utilisant la formule (14-8):
θ = FMM / R
ce qui exigerait le calcul de la réluctance R de ce circuit. Pour obtenir cette réluctance, il faudrait connaître la valeur de la perméabilité µr de la substance pour une densité de flux donnée.
On évite tous ces calculs en employant la courbe d'aimantation de la Fig. 14-12.
Celle-ci donne immédiatement le champ magnétique H requis pour produire, dans le circuit magnétique, une certaine densité de flux.
La section du noyau est:
A = 10 x 12 = 120 cm² = 0,012 m²
La densité de flux B est donc:
B = θ / A = 0,012 / 0,012 = 1 tesla
En se référant à la courbe de la Fig. 14-12, pour les tôles d'acier au Si (1 %), on voit qu'il faut un champ H de 300 A/m pour produire 1T.
La bobine doit donc produire une FMM de 300 A pour chaque mètre du circuit magnétique.
La longueur moyenne du circuit magnétique étant de 1,5 mètres, la force magnétomotrice de la bobine devra être:
FMM = 300 x 1,5 = 450 A ou 450 ampères-tours
Exemple 14-7
FMM requise poire un groupement en série.
Calculons maintenant la force magnétomotrice requise pour faire circuler le même flux (12 mWb) dans le noyau de l'exemple 14-6, après y avoir coupé une fente de 1,5 mm de longueur (Fig. 14-16a).
Figure 14-16
a. Circuit magnétique en série (voir exemple 14-7)
b. Circuit magnétique équivalent, montrant les FMM requises pour l'entrefer et les deux branches du noyau de fer

Solution
Il s'agit effectivement d'un groupement magnétique en série, car deux chemins de réluctance différente (acier et air) sont traversés par un même flux (analogie avec deux résistances disposées en série).
La FMM créée par la bobine est consommée par les chutes successives de «tension magnétique» dans chacun des chemins (Fig. 14-16b), tout comme la tension E appliquée à un circuit électrique est consommée par les chutes successives de tension dans les résistances groupées en série.
La FMM de la bobine est donc donnée par la somme des FMM nécessaires (a) pour l'air et (b) pour l'acier.
a) FMM pour l'air.
En supposant que dans la fente toutes les lignes suivent le même chemin qu'elles suivaient auparavant dans le fer, la densité de flux dans l'entrefer est la même que dans le noyau, soit 1T.
On a d'après l'équation 14-9:
FMM = 800 000 Bl = 800 000 x 1 x (1,5 / 1000) = 1200A
b) FMM pour l'acier.
La longueur du chemin magnétique dans l'acier étant sensiblement la même qu'auparavant:
1,5.0,0015 = 1,4985 m au lieu 1,5 m
la FMM requise pour l'acier est la même qu'auparavant, soit 450 A.
La force magnétomotrice de la bobine doit être :
FMM bobine = (1200 + 450) = 1650 A
Cet exemple démontre toute l'importance des entrefers dans les circuits magnétiques.
En effet, alors que dans ce cas la longueur du chemin est 1000 fois plus grande dans l'acier que dans l'air, l'acier requiert environ 2,5 fois moins d'ampères-tours que l'air.
Lorsque la longueur du chemin dans l'acier n'est pas trop grande par rapport à la longueur de l'entrefer, on peut négliger la FMM nécessaire pour l'acier.
Dans les machines électriques, on cherche à garder l'entrefer entre le rotor et le stator aussi étroit que possible afin de réduire la FMM que les pôles doivent développer.
En effectuant une réduction de la FMM, on peut diminuer la grosseur des bobines, ce qui contribue à réduire les dimensions et le coût de la machine.
Exemple 14-8
Groupement en parallèle.
Considérons le circuit magnétique de la Fig. 14-17a composé de noyaux de fonte et d'acier coulé.
Figure 14-17
a. Les noyaux de fonte et d'acier coulé sont en parallèle
b. Circuit magnétique équivalent (voir exemple 14-8)
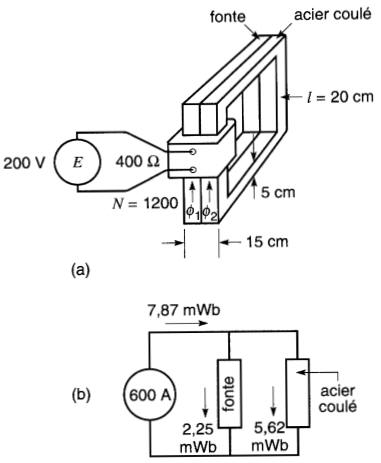
Le flux total provenant de la bobine est partagé entre les deux matériaux qui portent chacun ¢q et 02 lignes. Le circuit électrique équivalent (Fig. 14-17h) montre clairement que les chemins parcourus par 01 et 0, sont en parallèle.
Calculons la valeur (les flux 0 1 et 01 sachant que la bobine a une résistance de 400 S2 et comprend 1200 spires. La tension appliquée à la bobine est de 200 V et la longueur moyenne du chemin magnétique est de 20 cm.
Solution
Le courant dans la bobine vaut :
I = 200 V / 400Ω = 0,5 A
La FMM développée par la bobine vaut :
FMM = NI = 1200 x 0,5 = 600 A
Le champ magnétique H dans la fonte et dans l'acier coulé est donc :
H = FMM/l = 600 A/0,2 m = 3000 A/m
car la longueur du chemin magnétique (20 cm) est la même pour les deux matériaux.
Sur les courbes de saturation de la Fig. 14-12, on voit que ce champ magnétique crée des densités de flux B de 0,6 tesla pour la fonte et de 1,5 teslas pour l'acier coulé.
D'après la Fig. 14-17a, les deux noyaux possèdent la même section, soit:
A = 7,5 cm x 5 cm = 0,00375 m²
Donc:
θ1 = BA =
0,6 x 0,00375 = 0,00225 Wb = 2,25 mWb
θ2 = BA = 1,5 x 0,00375 = 0,00562 Wb = = 5,62 mWb
Exemple 14-9
Groupement composé
Le circuit magnétique de la Fig. 14-18a est un groupement composé, c'est-à-dire un arrangement de chemins magnétiques série-parallèle.
Figure 14-18
a. Circuit magnétique en série-parallèle (voir exemple 14-9)
b. Circuit magnétique équivalent
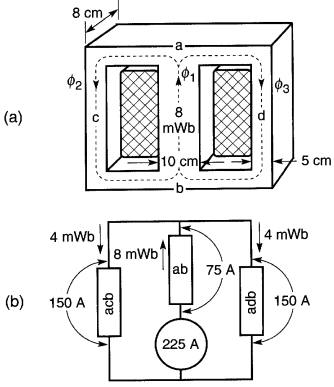
Le flux créé par la bobine passe par la jambe centrale ah et se divise en deux branches aci) et adb. Le circuit magnétique équivalent (Fig. 14-18b) montre clairement que les chemins acb et adb sont en parallèle.
Le noyau est composé de tôles d'acier au silicium (1 %) et les dimensions sont les suivantes:

Supposons que l'on désire créer un flux de 8 mWb dans la branche centrale ab du noyau (Fig.14-18a).
Quelle doit être la FMM de la bobine excitatrice?
Solution
Le flux θ1 dans la branche centrale se partage également entre les branches latérales acb et adb car ces deux branches ont la même longueur, la même section et par conséquent, la même réluctance.
Il s'ensuit que
θ2 = θ3 = θ1/2 = 8mWb/2 = 4 mWb
Une telle densité exige un champ de 300A/m (d'après la courbe pour l'acier au silicium, Fig. 14-12). La différence de potentiel magnétique entre les points a et b doit être de FMMacb = FMMadb = 300A/m x 0,5 m = 150 A
En d'autres termes, une FMM de 150 A est nécessaire pour faire passer un flux de 4 mWb à travers les chemins acb et adb.
La densité dans la branche centrale ab est:
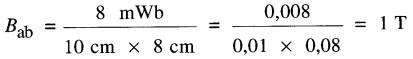
et elle nécessite également un champ magnétique de 300 A/m.
La FMM nécessaire pour le chemin ab est donc:
FMMab = 300A/m x 0,25 m = 75 A
La bobine doit donc produire une FMM totale de:
FMM = 150 + 75 = 225A
Il est important de remarquer qu'on ne doit pas additionner les FMM des branches adb et acb, car elles sont en parallèle et qu'elles sont donc soumises à une seule FMM commune.
FMM de même sens et de sens contraires
Les moteurs et les génératrices compound, les relais différentiels, les transformateurs et quelques démarreurs portent des enroulements dont les forces magnétomotrices peuvent être de même sens ou de sens contraires.
Par exemple, dans la Fig. 14-19, la règle de la main droite indique que les forces magnétomotrices des bobines X et Y agissent dans le même sens, de sorte que la FMM résultante est égale à la somme des deux FMM.
Figure 14-19 Les FMM des bobines agissent dans le même sens
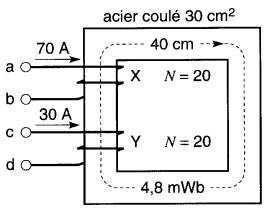
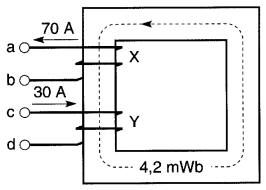
Par contre, si le sens du courant dans la bobine X est inversé (Fig. 14-20), les forces magnétomotrices agissent en sens contraires et la FMM résultante est égale à la différence des deux.
Figure 14-20 Les FMM des bobines agissent en sens contraires
Exemple 14-10
Calculer le flux dans le noyau en acier coulé des figures 14-19 et 14-20.
Le noyau a une section de 30 cm² et une longueur de 40 cm. Les bobines X et Y comptent 20 spires et les courants sont respectivement de 70A et 30A.
Solution
Pour la Fig. 14-19:
La FMM de la bobine X est :
FMMx = 70A x 20 spires = 1400A
La FMM de la bobine Y est:
FMMy = 30A x 20 spires = 600A
La FMM résultante est:
FMMx+y = (1400 + 600) = 2000A
d'où le champ magnétique:
H = 2000A / 40 cm = 2000 / 0,4 = 5000 A/m
D'après la courbe pour l'acier coulé (Fig. 14-12), la densité de flux vaut 1,6 teslas.
Le flux dans le noyau est donc:
θ = BA = 1,6T x 30cm² =1,6 x 30 x 10-4 = 4,8 mWb
Pour la Fig. 14-20:
Les FMM des bobines restent les mêmes mais elles agissent en sens contraires.
La FMM résultante est:
FMMx-y = (1400 - 600) = 800 A
d'où le champ magnétique:
H = 800A / 40 cm = 800 / 0,4 = 2000A/m
D'après la courbe pour l'acier coulé (Fig. 14-12), la densité de flux vaut 1,4 teslas.
Le flux dans le noyau est donc:
θ = BA = 1,4T x 30cm² =1,4 x 30 x 10-4 = 4,2 mWb
Le sens du flux est l'inverse de celui de la Fig. 14-19 car la FMM de la bobine X est supérieure à celle de la bobine Y.
Flux de fuite
Dans les circuits magnétiques industriels, les lignes ne restent pas toutes canalisées à l'intérieur du circuit désigné. Par exemple, dans la Fig.14-21, une partie des lignes passe en dehors du noyau de fer et de l'entrefer. Le flux correspondant à ces lignes qui s'échappent dans l'air se nomme flux de fuite.
Ce flux de fuite prend plus d'importance quand le circuit magnétique devient saturé. Lors de l'étude des transformateurs, nous verrons l'effet de ces flux de fuite.
Le SI, le système CGS et le système anglais
La majorité des calculs de circuits magnétiques se font avec les unités SI. Toutefois, on rencontre parfois l'ancien système métrique CGS (centimètre-gramme-seconde), dans lequel les principales unités magnétiques sont l'rsted, le gauss et le gilbert .
Le gauss est une unité de densité de flux valant une ligne par centimètre carré, ou 0,1 millitesla.
L'rsted est une unité de champ magnétique valant 1000/471 A/m, ou 80 A/m environ. 1 rsted = 80 A/m
Le gilbert est une unité de force magnétomotrice valant 0,4 7t A, ou 1,26 A environ.
1 gilbert = 1,26 A
Dans le système CGS la perméabilité du vide est égale à 1.
La relation entre le champ magnétique H, la densité de flux B et la perméabilité relative µr est donc la suivante:
B = µrH (14-9)
B est exprimé en gauss,
H, en rsted.
Dans le système anglais, il suffit de retenir que 108 lignes = 1 weber
et que
64 516 lignes/pouce² = 1 tesla
Exemple 14-11
Un champ magnétique de 3 rsteds produit une densité de flux de 12 000 gauss dans un échantillon d'acier.
Exprimer ces grandeurs en unités SI et calculer la perméabilité relative du matériau.
Solution
Le champ magnétique de 3 rsteds vaut :
H= 3 x 80 = 240 A/m
La densité de flux de 12 000 gauss vaut :
B = 12 000 X 0,1 = 1200 milliteslas = 1,2 T
d'où la perméabilité relative
µr = B/H = 12 000 gauss/3 rsted = 4000
Résumé
Dans cette section nous avons noté la grande analogie entre circuits électriques et circuits magnétiques.
Un circuit magnétique est constitué d'éléments reliés les uns aux autres de façon à conduire un flux magnétique. Un circuit magnétique soumis à une force magnétomotrice NI est parcouru par un flux.
L'intensité du flux dépend
1) de la longueur du chemin magnétique
2) de la section du chemin magnétique et
3) de la perméabilité du matériau utilisé.
Le rapport entre le flux obtenu dans le noyau et celui qu'on obtiendrait dans l'air s'appelle la perméabilité relative µr. La perméabilité magnétique du fer doux est supérieure à 1000 et peut dépasser 100 000 pour certains alliages spéciaux.
Le champ magnétique H en un point est la force magnétomotrice par unité de longueur.
Dans le SI il est exprimé en ampères par mètre (A/m). Pour l'air et les matériaux non magnétiques, la densité de flux B est proportionnelle à H (B = µoH). Pour un matériau magnétique, B est en plus majorée par la perméabilité relative (B = µrµoH).
Pour chaque type de matériau magnétique, cette dernière relation est présentée sous forme d'une courbe B-H.
À cause du phénomène de saturation, la courbe B-H n'est pas linéaire, ce qui revient à dire que la perméabilité relative n'est pas constante.
Enfin, nous avons vu qu'en appliquant trois formules de base gouvernant la circulation d'un flux θ dans un circuit magnétique de section A, de longueur 1 et soumis à une force magnétomotrice NI, soit:
B = θ/A, B = µrµoH et H = NI/l
il est possible de résoudre des circuits les plus complexes. Il peut s'agir d'un circuit série (par exemple un noyau avec entrefer), d'un circuit parallèle, ou d'un circuit composé. Le circuit magnétique peut également comprendre plusieurs forces magnétomotrices.
PROBLÈMES
Niveau pratique
14-1 Qu'est-ce qu'un circuit magnétique?
14-2 Que veut dire réluctance d'un circuit magnétique?
14-3 Comment varie la réluctance d'un circuit magnétique en fonction de sa longueur?
14-4 Donner les unités SI pour: a) densité de flux b) champ magnétique c) flux magnétique
14-5 Qu'entend-on par coefficient de perméabilité d'un matériau magnétique?
14-6 Expliquer pourquoi le fer est plus perméable que l'air.
14-7 Pourquoi le fer se sature-t-il?
14-8 Faire une analogie entre les circuits électriques et les circuits magnétiques.
14-9 Si la densité de flux dans le noyau magnétique d'un transformateur ne doit pas dépasser 1,5 T, quelle doit être sa section minimum, le flux total étant de 0,3 Wb?
14-10 Un pôle de moteur aune section de 20 cm² et doit porter un flux de 2,4 mWb. Quelle sera la densité de flux?
14-11 Le flux à l'intérieur d'une bobine toroïdale est de 20 µWb. Quand on place un noyau d'acier doux à l'intérieur de cette bobine, le flux augmente à 60 mWb. Trouver la perméabilité relative du noyau.
14-12 Dans la Fig. 14-19, si les bobines X et Y portent chacune un courant de 50 A, quelle est la FMM totale développée par les deux bobines?
Niveau intermédiaire
14-13 En se référant à la Fig. 14-12, quel est le champ magnétique requis pour établir une densité de flux de 1,4 T: a) dans l'acier au silicium? b) dans l'acier coulé? c) dans le vide?
14-14 En se référant à la Fig. 14-12 et en utilisant la formule (14-7), calculer la perméabilité relative dans les cas suivants :
a) acier au silicium à une densité de 1,4 T et 1,6 T
b) acier coulé à une densité de 0,7 T et 1,4 T
c) fonte à une densité de 0,2 T et 0,6 T
14-15 Combien d'ampères-tours sont requis pour un entrefer de 2 mm de longueur dans lequel on maintient une densité de flux de 1,5 T?
14-16 Soit un noyau d'acier coulé ayant la forme donnée à la Fig. 14-4a. Calculer la densité de flux dans le noyau, de même que le flux total, sachant que la bobine de 800 spires porte un courant de 12,5 A.
14-17 Dans le problème 14-16, quel serait le flux si l'on utilisait de la fonte?
14-18 Dans le problème 14-16, quel serait le flux si l'on enlevait le noyau d'acier complètement?
14-19
a) En se référant à la Fig. 14-13, calculer la perméabilité du Permalloy pour les champs magnétiques suivants: 4 A/m, 400 A/m, 40 kA/m.
b) Pour quelle densité de flux la perméabilité du nickel est-elle égale à celle de l'alnico V?
14-20 Un noyau de fonte, ayant la forme donnée à la Fig. 14-15, est excité par une bobine possédant 250 spires. Si l'on désire créer un flux de 7,2 mWb, calculer le courant d'excitation requis .
14-21 Dans le problème 14-20, si le noyau possède un entrefer de 12,5 mm, calculer le courant d'excitation requis pour créer le même flux .
14-22 Dans la Fig. 14-20, si le courant dans la bo- bine X est de 70 A, quel courant doit-on faire circuler dans la bobine Y afin que le flux devienne nul?
Niveau avancé
14-23 En se référant à la Fig. 14-13, déterminer la perméabilité relative des matériaux dans les cas suivants :
a) acier pour relais, lorsqu'il est soumis à un champ de 100 A/m
b) le verre, lorsqu'il porte une densité de flux de 1,25 T.
14-24 On désire créer une densité de flux de 0,7 T dans l'entrefer de la génératrice montrée à la Fig . 13-17.
Sachant que la longueur de chaque entrefer est de 3 mm, calculer la FMM total que les bobines doivent développer (négliger la FMM requise pour le noyau).
14-25 L'électro-aimant en fer à cheval montré à la Fig. 13-23a les caractéristiques suivantes :
1) nombre de spires par bobine : 150
2) longueur du fer à cheval (en acier coulé): 250 mm
3) longueur de l'armature (en acier au silicium): 50 mm
4) section du fer à cheval, de l'armature et de chaque entrefer: 100 mm²
5) longueur de chaque entrefer : 1 mm
On désire créer une densité de flux de 1,4 T dans l'entrefer. Calculer le courant d'excitation requis.
14-26 En se référant à la Fig. 13-25, on sait que les pôles et le noyau de fer sont faits en acier coulé ayant la courbe d'aimantation donnée à la Fig. 14-12.
Le noyau a une section de 1,9 m x 4,5 m, et les pôles ont un diamètre de 4,67 m. On désire établir un flux de 12 Wb dans l'entrefer, en excitant les bobines principales seulement.
Calculer:
a) la FMM requise pour l'entrefer
b) la FMM requise pour les deux pôles et la densité de flux correspondante
c) la FMM requise pour chaque jambe latérale du noyau de fer (prendre une longueur de 22 m) et la densité de flux correspondante
d) la FMM totale créée par l'ensemble des deux bobines
e) le courant d'excitation requis dans chaque bobine.
14-27 a) Refaire les calculs du problème 14-26 pour un flux de 27,4 Wb. b) l'acier est-il saturé dans ces circonstances? c) Quelle est la puissance requise pour exciter les bobines principales?
14-28 Dans la Fig. 13-5
a) calculer la FMM créée par le conducteur de cuivre
b) calculer la circonférence du cercle en pointillé ayant un rayon de 10 cm
c) de (a) et (b), déduire la valeur du champ magnétique H
d) calculer la densité de flux à 10 cm du centre du conducteur
e) comparer (d) avec la valeur donnée par la formule (13-1)
14-29 Dans la Fig. 16-8, les aimants permanents N et S produisent une FMM totale de 15 000 A. La longueur de l'entrefer est de 4 cm. Calculer la densité de flux B.
Réponses
9) 0,2 m²; 10) 1,2 T; 11) 3000;
12) 2000 A; 13a) 1 kA/m;
13b) 2 kA/m; 13c) 1120 kA/m; 14a) 1120; 512; 14b)
1120; 560;
14c) 320; 160; 15) 2400 A; 16) 1,6 T; 160 µWb; 17) 70 µWb;
18)
0,625 µWb; 19) 250 000; 2500; 25; 19b) 0,61 T; 20) 18 A;
21) 42 A; 22) 70 A;
23a) 4800; 23b) 1,0; 24) 3360 A; 25) 9,3 A;
26a) 170,8 kA; 26b) 2512 A; 0,7
T; 26c) 11 kA; 26d) 184,3 kA;
26e) 70,9 A; 27a) 525,5 kA total; 202 A; 27b)
oui; 1,6 T;
27c) 50,6 kW; 28a) 10 A; 28b) 0,628 m; 28c) 15,92 A/m;
28d)
19,9 µT; 28e) 20 µT; 29) 0,47 T
