Circuits simples à courant alternatif

Électrotechnique

Dans cette section, nous décrivons les propriétés des ondes sinusoïdales. Nous établissons la forme d'onde du courant résultant de l'application d'une tension sinusoïdale à un circuit résistif, un circuit capacitif et un circuit inductif. Cela nous amène aux notions de réactance inductive, réactance capacitive, puissance active et puissance réactive.

Cette section introduit donc les principes fondamentaux des circuits à courant alternatif.

Forme d'onde sinusoïdale

Lors de l'étude de l'alternateur élémentaire (section Tension induite dans un conducteur) nous avons vu qu'un aimant permanent tournant à une vitesse constante à l'intérieur d'un cadre produit une tension alternative aux bornes de ce cadre.

On a aussi montré qu'il est possible de changer la forme d'onde de la tension en modifiant la forme des pôles de l'aimant. Il est donc possible d'obtenir une très grande variété de formes d'onde en changeant les pôles de l'alternateur.

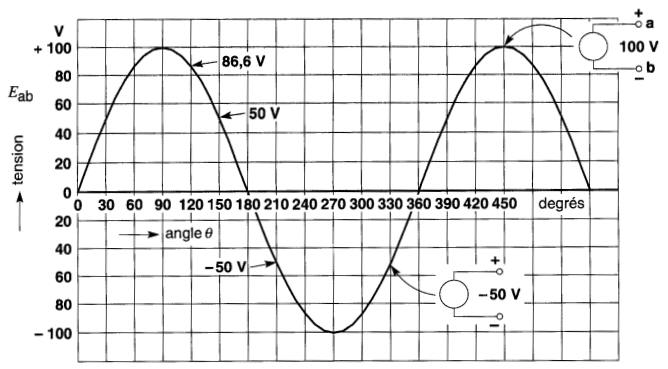
Cependant, il existe une forme d'onde qui nous intéresse particulièrement parce qu'elle est la plus simple des courbes périodiques: c'est la courbe sinusoïdale. On a tracé à la Fig. 22-1 la courbe d'une tension sinusoïdale dont la valeur crête est de 100V.

Figure 22-1 Forme d'onde d'une tension sinusoïdale ayant une valeur crête de 100V

La courbe donne la valeur de la tension induite dans le cadre pour chacune des positions occupées par l'aimant tournant. Ces positions successives sont repérées par l'angle en degrés dont l'aimant a tourné par rapport à sa position originale. On remarque que la tension part d'une valeur nulle et croît rapidement pour atteindre une valeur maximale à un angle de 90°.

Si cette valeur maximale, ou valeur crête, est de 100V, la tension sera de 50V à 30° et 86,6V à 60°. Après avoir atteint la valeur crête, la tension décroît pour passer par les valeurs de 86,6V à 120°, de 50V à 150°, et elle s'annule enfin à 180°.

Puis la polarité de la tension change de signe ; la tension passe successivement par des valeurs négatives: -50V à 210°, -86,6V à 240° et -100V à 270°.

Elle atteint finalement une valeur nulle à 360°, après quoi un nouveau cycle commence et la tension passe par la même suite de valeurs pendant le même temps.

Dans toute onde sinusoïdale les mêmes proportions se retrouvent. Ainsi, une tension dont la valeur crête est de 150V aura une valeur égale à 50 % de 150V à 30° et une valeur égale à 86,6 % de 150V à 60°.

Pourquoi choisit-on une onde sinusoïdale plutôt qu'une onde «simple» comme une onde carrée ou triangulaire?

Voici quelques raisons :

a) Dans les machines à courant alternatif, c'est l'onde sinusoïdale de tension qui occasionne le moins de pertes. Le rendement est donc meilleur.

b) Une onde sinusoïdale de tension ou de courant produit moins d'interférence (bruit) sur les lignes téléphoniques.

c) Dans les circuits à courant alternatif, une tension sinusoïdale produit un courant sinusoïdal et vice-versa. C'est la seule onde possédant cette propriété de se «reproduire».

d) Dans les moteurs électriques, un flux variant sinusoïdalement produit moins de bruit.

De plus, le couple durant le démarrage est plus régulier.

Mathématiquement, une tension sinusoïdale est décrite par l'équation:

e = E_m sin θ    (22-1)

où

e = valeur instantanée de la tension [V]
E_m = valeur crête de la tension [V]
θ = angle de rotation [°]

De la même façon, un courant sinusoïdal est donné par la formule:

i = I_m sin θ    (22-2)

dans laquelle les symboles ont une signification analogue.

Une grandeur sinusoïdale, comme une tension, change le plus rapidement lorsqu'elle passe par zéro. Le taux de variation à cet instant est donné par la formule:

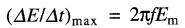    (22-3)

où

(ΔE/Δt)_max = taux de variation maximal de la tension en volts par seconde [V/s]

f = fréquence de la tension [Hz]

E_m = valeur maximale de la tension [V]

π = 3,1416

Une expression comparable s'applique pour un courant sinusoïdal. Nous donnons à la section ci-dessous, la relation entre l'angle de rotation 0, la fréquence f, et le temps t.

 CIRCUIT RÉSISTIF

Soit un alternateur produisant une tension sinusoïdale dont la valeur crête est de 100V.

Celui-ci alimente une résistance de 10Ω (Fig. 22-2). Supposons que le courant soit positif lorsqu'il circule de la borne a à la borne b dans la résistance.

Figure 22-2 Dans un circuit résistif, le courant est en phase avec la tension

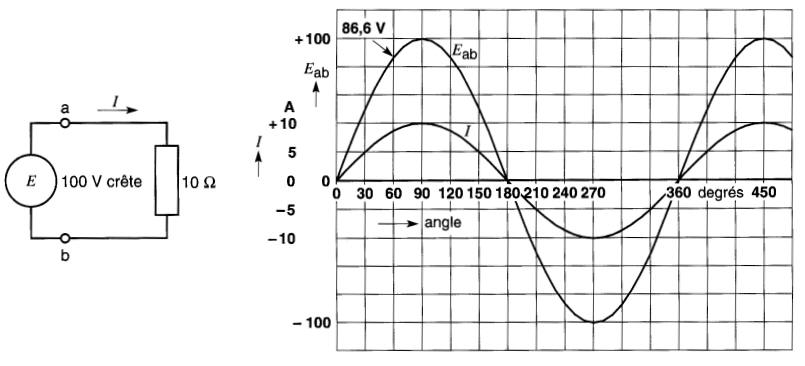
Pour déterminer l'allure de la courbe du courant, appliquons la loi d'Ohm pour quelques valeurs instantanées de la tension.

Tout d'abord, à 0°, 180° et 360°, la tension étant nulle, le courant est également nul.

À l'angle de 30°, Eab = +50V (a est positif par rapport à b) et un courant de 50V/10Ω= 5A circule dans le sens positif.

À l'angle de 60°, Eab = +86,6V, le courant devient 86,6V/10Ω = 8,66A.

On trouve de la même façon la valeur du courant à 90°, 120° et 150°.

À 210°, Eab =-50V (a est négatif par rapport à b) et le courant doit circuler de b à a dans la résistance, soit dans le sens négatif:

I = -50/10 = -5A.

À 270°, le courant sera: -100V/10Ω =-10A.

Avec ces quelques points, on peut tracer la courbe du courant en fonction de l'angle parcouru. On constate que la forme d'onde obtenue est également sinusoïdale.

En étudiant la courbe de la tension appliquée et celle du courant résultant, on voit que toutes deux passent par une valeur nulle en même temps, et qu'elles atteignent leur valeur maximale positive au même instant. On dit alors que la tension et le courant sont en phase.

Puissance dissipée dans une résistance

Nous avons vu que la puissance P dissipée par effet Joule dans une résistance est donnée par le produit de la tension E à ses bornes et du courant I qui la traverse.

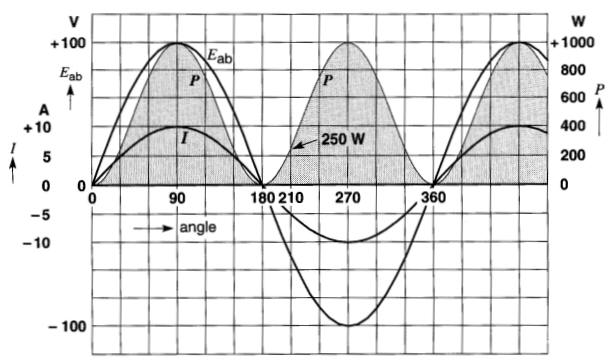
On peut appliquer la même formule au circuit de la Fig. 22-2: en multipliant à chaque instant les valeurs de la tension par les valeurs correspondantes du courant, on peut tracer la courbe de variation de la puissance P (Fig. 22-3).

Figure 22-3 La puissance dissipée dans une résistance par un courant alternatif varie périodiquement. La valeur moyenne de cette puissance est égale à la moitié de la valeur maximale

À 0°, la tension et le courant sont nuls ; il en est de même pour la puissance.

P = 0 watt

À90°, Eab=+100V, I=+10A

la puissance vaut:

P = (+100V) x (+10A)=+1000W

Si l'on procède ainsi pour différentes valeurs d'angles comprises entre 0 et 180°, on trouve que la puissance part de zéro, atteint une valeur maximale de 1000 W et retombe à zéro (Fig. 22-3). Lorsque la tension et le courant deviennent négatifs, la puissance reste positive car le produit de deux nombres négatifs est positif.

Ainsi, à 210°, Eab = -50V, I = -5A

d'où P = (-50V) x (-5A) = +250 W

On voit que la puissance atteint une valeur maximale de 1000 W, décroît, s'annule, croît de nouveau, et ainsi de suite.

La puissance dissipée dans la résistance est variable, mais elle possède une valeur moyenne de 1000 W/2 = 500 W. On dit que la résistance dissipe une puissance active de 500 W.

Valeur efficace d'une tension ou d'un courant sinusoïdal

Il est opportun d'établir ici l'équivalence entre une tension alternative et une tension continue, du point de vue de leurs effets thermiques. On peut se demander si une tension alternative sinusoïdale de 100V crête correspond à une tension continue de 100V.

 Considérons alors les exemples suivants.

Un alternateur produisant une tension sinusoïdale de 100V crête alimente une résistance de 10Ω (Fig. 22-4).

Figure 22-4 Puissance dissipée lorsqu'une tension sinusoïdale de 100 V crête est appliquée à une résistance de 10Ω

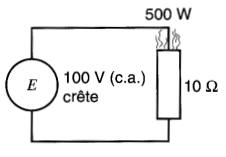
Remplaçons l'alternateur par une source de tension continue dont la valeur est de 100V (Fig. 22-5).

Figure 22-5 Puissance dissipée lorsqu'une tension continue de 100 V est appliquée à la même résistance

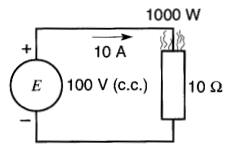
Si ces deux tensions étaient équivalentes au point de vue thermique, elles produiraient le même dégagement de chaleur dans la résistance.

Mais on sait que la puissance moyenne dissipée dans le premier cas n'est que de 500 W, alors qu'elle est constante et égale à 1000 W dans le second cas. On doit conclure que les deux tensions ne sont pas équivalentes.

Quelle tension continue doit on appliquer afin que la résistance de 10Ω dissipe 500 W ?

On trouve la réponse en utilisant la formule 4-4 section Puissance et énergie électrique:

P = E² / R

Soit:

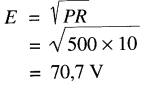
Donc, une tension continue de 70,7V produit le même dégagement de chaleur dans la résistance de 10 S2 qu'une tension sinusoïdale dont la valeur crête est de 100 V (Fig. 22-6).

Figure 22-6 Une tension continue de 70,7V provoque le même échauffement qu'une tension sinusoïdale de 100 V crête. La valeur efficace de la tension alternative est donc de 70,7V

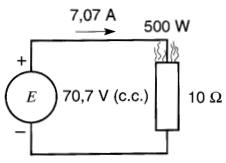
On dit que la valeur efficace de cette tension sinusoïdale est de 70,7V.

Par définition, la valeur efficace d'une tension alternative est égale à la valeur d'une tension continue qui provoquerait le même échauffement dans une même résistance. La valeur efficace d'une tension sinusoïdale ou d'un courant sinusoïdal est toujours égale, à 0,707 (ou 1/2) fois sa valeur crête.

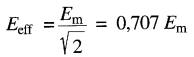    (22-4)

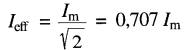    (22-5)

Presque tous les instruments de mesure à courant alternatif sont calibrés de façon à indiquer la valeur efficace d'une tension ou d'un courant, et non la valeur crête. Quand on donne la valeur d'une tension alternative ou d'un courant alternatif, il est entendu que c'est la valeur efficace.

Le mot «efficace» d'une tension ou d'un courant est parfois désigné par les lettres rms («root mean square»). Ainsi on peut dire que la valeur rms d'une tension est de 120V.

En ce qui concerne les tensions et courants périodiques mais non sinusoïdaux, on donne à la section plus loin la façon de calculer leurs valeurs efficaces.

Exemple 22-1

Un voltmètre à courant alternatif indique que la tension dans une résidence est de 120V, 60 HZ.

Calculer:

a) la valeur crête de la tension
b) la valeur minimale de la tension
c) le taux de variation maximal

Solution

a) L'instrument indique la valeur efficace de la tension. Sa valeur crête est 120 - 0,707 = 169,7V.
(La forme d'onde de cette tension apparaît à la Fig. 17-16 section Tension induite dans un conducteur).

b) La valeur minimale de la tension est évidemment zéro.

c) Le taux de variation maximal est obtenu à partir de l'équation 22-3:

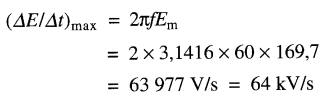
L'emploi des valeurs efficaces de tension et de courant permet de résoudre les circuits résistifs à courant alternatif par les mêmes méthodes que celles utilisées pour les circuits à courant continu.

Exemple 22-2

Une tension efficace de 100V est appliquée a une résistance de 50Ω.

Calculer :

a) le courant efficace

b) la puissance dissipée par la résistance

Solution

Le courant efficace est:

I_eff =  E_eff / R = 100 / 50 = 2A

La puissance dissipée dans la résistance vaut :

P= E_eff x I_eff= 100V x 2A =2 00W

Circuit capacitif

Dans ce qui suit, nous verrons qu'une tension sinusoïdale appliquée à un circuit capacitif produit un courant qui a également une forme d'onde sinusoïdale.

Cependant, ce courant capacitif est déphasé de 90° en avance sur la tension. Afin d'éviter une présentation trop théorique, nous utiliserons un exemple numérique pour expliquer ce qui se produit dans un circuit capacitif. Nous donnerons ensuite les formules requises pour résoudre ce genre de circuit.

Un condensateur de 100 µF est relié à un alternateur qui produit une tension sinusoïdale de 100V crête à une fréquence de 60 Hz (Fig. 22-7).

Figure 22-7 Une tension sinusoïdale appliquée à un condensateur produit un courant sinusoïdal déphasé de 90° en avance sur la tension

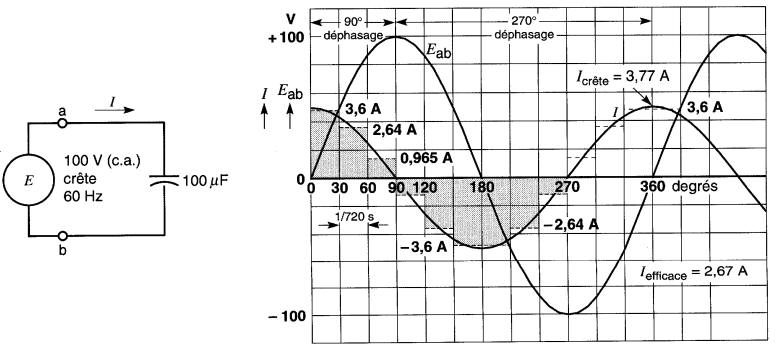
Le sens positif du courant est indiqué sur le schéma. La durée d'un cycle (360°) étant de 1/60e de seconde, chaque intervalle de 30° dure 1/720 s.

Pour déterminer l'allure de la courbe du courant, nous calculons la valeur moyenne du courant pour chaque intervalle de 30 degrés. Cette valeur nous est donnée parla formule 21-7:

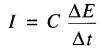
Intervalle de 0 à 30° : la tension part de zéro et atteint une valeur de 50V en 1/720 s. Le courant moyen est de:

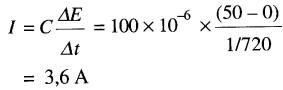
Étant donné que Eab est positif durant cet intervalle de temps, le courant circule dans le sens positif et le condensateur se charge.

Intervalle de 30° à 60°: la tension croît de 50V à 86,6V Le courant moyen est alors de:

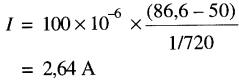
Le condensateur se charge davantage; le courant est toujours positif.

Intervalle de 60° à 90°: la tension passe maintenant de 86,6V à 100V, soit une variation de 13,4 V.

Le calcul donne un courant moyen de 0,965A.

Intervalle de 90° à 120° : la variation de tension est encore de 13,4V, et le courant moyen est toujours de 0,965A. Cependant la tension diminue, le condensateur se décharge et le courant change de sens. Sa valeur est donc de -0,965A.

En procédant ainsi, on peut trouver les courants moyens correspondant à chacun des intervalles pendant un cycle et porter ces valeurs sur le graphique de la Fig. 22-7. La courbe de courant ainsi obtenue est composée d'une série de paliers.

Si les intervalles de temps considérés avaient été plus courts, le nombre de paliers aurait été plus grand et la courbe plus régulière.

Si l'on joint les centres de ces paliers, la courbe obtenue est une sinusoïde.

La valeur crête de cette sinusoïde correspond à une intensité d'environ 3,7A. On peut déterminer la valeur exacte de ce courant maximal à l'aide de la formule (22-3). On s'aperçoit que le courant est maximal lorsque la tension passe par zéro. Or, le taux de variation de la tension à ce moment est:

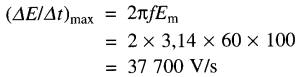
Le courant maximal est donc:

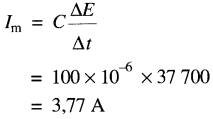
Le courant efficace dans le circuit est donc 0,707 x 3,77A, soit 2,67A.

On remarquera, sur le graphique, que le courant est nul lorsque la tension est maximale, et inversement, que le courant atteint sa valeur maximale lorsque la tension est nulle.

On pouvait prévoir ce résultat en se rappelant que le courant dans un circuit capacitif ne dépend pas de la valeur de la tension appliquée au condensateur, mais bien de la vitesse de variation de cette tension.

On notera de plus que le courant atteint sa valeur maximale positive de 90° (ou un quart de cycle) avant que la tension atteigne elle-même sa valeur maximale positive. Le courant capacitif est déphasé de 90° en avance sur la tension.

Inversement, on peut dire que la tension est déphasée de 90° en arrière du courant. Le déphasage entre deux courbes sinusoïdales se mesure par le nombre de degrés qui sépare leurs crêtes positives successives.

Ainsi, en se référant à la Fig. 22-7, on pourrait également dire que la tension est déphasée de 270° en avance sur le courant.

Cependant, en pratique, on spécifie le déphasage par un angle inférieur à 180°.

Réactance capacitive

Si l'on introduit un voltmètre et un ampèremètre dans le circuit précédent, ils indiqueront respectivement une tension efficace de 70,7V et un courant efficace de 2,62A (Fig. 22-8).

Figure 22-8 Tension et courant dans un circuit capacitif

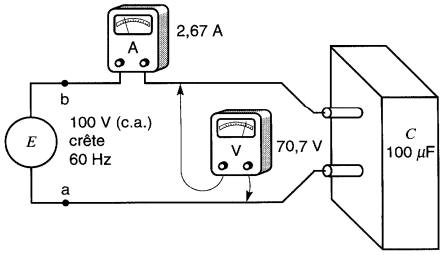
Il semble donc que la «résistance» du condensateur soit de:

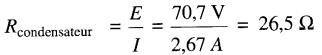
Cependant, on évite la possibilité de confusion avec les circuits résistifs en appelant réactance capacitive le rapport entre la tension et le courant d'un condensateur.

La réactance capacitive (symbole X_c est exprimée en ohms, et sa valeur change avec la fréquence de la source. La réactance capacitive d'un condensateur est donnée par la formule suivante:

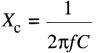    (22-6)

où

X_c = réactance capacitive, en ohms [Ω]
f = fréquence de la source, en hertz [Hz]
C = capacitance du condensateur, en farads [F]
π = 3,1416

Ainsi, dans l'exemple précédent, la valeur de X_c pour le condensateur de 100µF à une fréquence de 60 Hz est:

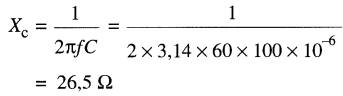
La formule 22-6 indique que la réactance capacitive d'un condensateur diminue à mesure que la fréquence et la capacitance augmentent. Donc un condensateur laisse d'autant mieux passer le courant que sa capacitance est plus grande et que la fréquence est plus élevée.

Exemple 22-3

n condensateur de 10µF est raccordé à une source de tension dont la valeur efficace est de 100V.

Si la fréquence est de 200 Hz, quel est le courant efficace dans le circuit?

Solution

On calcule d'abord la réactance capacitive du condensateur:

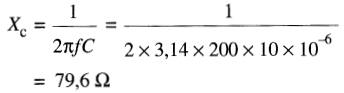
La réactance du condensateur étant de 79,6 £2, le courant efficace dans le circuit vaut :

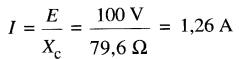
Puissance réactive dans un condensateur: le var capacitif

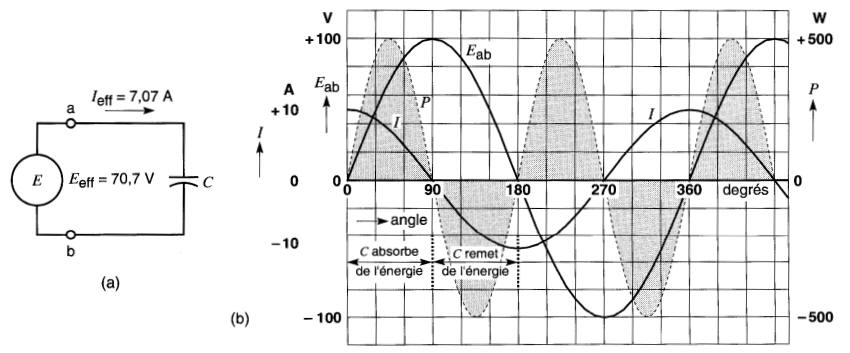
La Fig. 22-9a représente un condensateur parcouru par un courant dont la valeur efficace est de 7,07A (10A crête) quand il est soumis à une tension efficace de 70,7V.

Figure 22-9 a Tension et courant efficaces dans un circuit capacitif b_ Courbes de tension, courant et puissance instantanés

À la lecture d'un ampèremètre et d'un voltmètre affichant ces valeurs, on pourrait croire que la puissance dissipée dans le condensateur est :

P = EI =70,7V x 7,07A = 500W

Essayons toutefois de vérifier ce résultat à l'aide des courbes de la Fig. 22-9b.

L'une de ces courbes (Eab) représente la tension appliquée au condensateur, l'autre (I) indique les valeurs successives du courant qui le parcourt.

Comme dans le cas des circuits résistifs, nous avons tracé la courbe (P) de la puissance en multipliant les valeurs instantanées de la tension par les valeurs correspondantes du courant.

Par exemple, à 150°:

Eab = +50V, I = -8,66A

d'où P = (+50V) x (-8,66A) = -433W

En examinant cette courbe en pointillés, on se rend compte que durant le premier quart de cycle, entre 0° et 90°, la puissance est positive, c'est-à-dire qu'une certaine quantité d'énergie est fournie par la source et emmagasinée dans le condensateur.

Durant le quart de cycle suivant, entre 90° et 180°, la puissance est négative: le condensateur restitue maintenant à la source l'énergie qu'il avait absorbée.

On voit donc qu'il y a un échange continuel d'énergie entre la source et le condensateur, de sorte que la valeur moyenne de la puissance fournie par la source est nulle.

Le produit de la valeur efficace du courant dans un condensateur et de la valeur efficace de la tension appliquée à ses bornes est appelé puissance réactive capacitive (symbole Q_c).

L'unité de puissance réactive capacitive est le volt-ampère réactif(symbole var). Il est important de noter que la puissance réactive associée à un condensateur se mesure en vars et non pas en watts.

La puissance réactive Q_c mise en jeu dans le circuit de la Fig. 22-9a est donc de 500 var et non pas de 500 W. De plus, cette puissance réactive ne produit aucun dégagement de chaleur dans le condensateur.

La Fig. 22-10 montre une application importante des condensateurs.

Figure 22-10 Groupe de 18 condensateurs ayant une capacité totale de 2,7 Mvar sous une tension de 14,4 kV, 60 Hz. Ils sont installés sur le réseau de la South Carolina Electric and Gas Company pour régulariser la tension de la ligne (gracieuseté de Cie Generale Electrique du Canada)

Circuit inductif

Nous verrons dans cette section qu'une tension sinusoïdale appliquée à une bobine donne naissance à un courant dont la forme d'onde est également sinusoïdale. Ce courant est déphasé de 90° en arrière de la tension. Nous utiliserons à nouveau un exemple numérique pour expliquer ce qui se produit dans un circuit inductif.

Supposons qu'un courant sinusoïdal de 10A crête, 60 Hz, traverse une bobine dont l'inductance est de 0,1 henry (Fig. 22-11).

Figure 22-11 Une tension sinusoïdale appliquée à une inductance produit un courant sinusoïdal déphasé de 90° en arrière de la tension

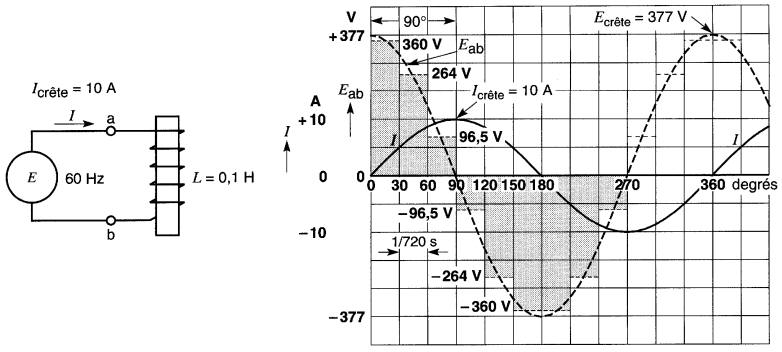
Pour déterminer l'allure de la courbe de la tension à ses bornes, on peut calculer la valeur moyenne de cette tension pour chaque intervalle de temps correspondant à un angle de 30°.

Cette valeur de tension est donnée par la formule 19-4:

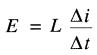
Intervalle de 0° à 30°:

le courant croît de 0 à 5A, et la durée de cette variation de 30° est 1/720 s, car la durée d'un cycle (360°) est 1/60 s. La valeur moyenne de la tension induite pendant cet intervalle est :

E_ab = L ΔI/Δt = 0,1 x (5 - 0) x 720 = 360V

Le courant étant positif et croissant, il s'ensuit que la borne a est positive, donc E_ab = +360V.

Intervalle de 30° à 60° :

le courant croît de 5 à 8,66A; la valeur moyenne de la tension induite est alors :

Le courant étant positif et croissant, il s'ensuit que la borne a est positive, donc E_ab = +360V.

Intervalle de 30° à 60° :

le courant croît de 5 à 8,66A; la valeur moyenne de la tension induite est alors :

E_ab = L ΔI/Δt = 0,1 x (8,66 - 5) x 720 = 264V

La polarité de la tension induite Eab est encore positive car le courant augmente dans le même sens que précédemment.

 Intervalle de 60° à 90°:

le courant passe de 8,66 à 10,0A. soit une variation de 1,34A, d'où:

E_ab =L ΔI/Δt = 0,1 x 1,34 x 720 = 96,5V

Intervalle de 90° à 120°: le courant décroît de 10A à 8,66A; par conséquent, la variation du courant est encore de 1,34A, et la valeur moyenne de la tension est de nouveau 96,5V.

Cependant, la diminution du courant entraîne une diminution du flux dans le noyau : la tension induite E_ab devient alors négative. E_ab = -96,5V.

En procédant de cette façon, on peut trouver la valeur moyenne de la tension induite pour chaque intervalle de 1/720 s considéré durant un cycle.

Si l'on porte les valeurs ainsi obtenues sur un graphique (Fig. 22-11), il en résulte une courbe composée d'une série de paliers, comme dans le cas du courant dans un condensateur.

En joignant les centres de ces paliers on obtient une courbe à peu près sinusoïdale. La valeur crête de cette courbe correspond à une tension d'environ 370V.

On peut déterminer la valeur exacte de cette tension maximale en se référant à la formule (22-3).

En effet, on s'aperçoit que la tension est maximale lorsque le courant passe par zéro. Or, le taux de variation du courant à ce moment est donné par une expression analogue à la formule (22-3).

On obtient donc

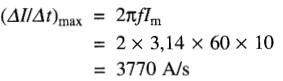
Par conséquent, la tension maximale exacte est

E_m = L ΔI/Δt = 0,1 x 3770 = 377V

La tension efficace aux bornes de la bobine est donc de 0,707 x 377V, soit 267V. Pour simplifier l'analyse du circuit inductif, nous avons trouvé la valeur de la tension induite E_ab à partir de la valeur du courant.

Il convient de remarquer que ce courant produit en réalité par la tension E_ab de la source. Cependant, en se référant au circuit de la Fig. 22-11, il clair que la tension E_ab de la source est nécessairement égale à la tension E_ab induite. On constate donc qu'une tension sinusoïdale appliquée à une inductance produit un courant sinusoïdal.

De plus, on remarque que le courant inductif est nul lorsque la tension est maximale et, inversement, que le courant est maximal lorsque la tension est nulle. Le courant inductif atteint sa valeur maximale positive à un angle de 90° (ou un quart de cycle) après que la tension ait atteint sa valeur maximale positive.

Comme pour le courant capacitif, le courant inductif est déphasé de 90° par rapport à tension, mais cette fois-ci, il est en arrière de la tension.

Réactance inductive

Tout comme pour une résistance, l'opposition offerte par la bobine au passage du courant est caractérisée par le rapport E/I entre la valeur efficace de la tension et la valeur efficace du courant.

Ce rapport est appelé réactance inductive (symbole X_L) de la bobine, et il s'exprime en ohms.

Si l'on introduit un ampèremètre et un voltmètre dans le circuit de l'exemple précédent, les instruments indiqueront les valeurs suivantes (Fig. 22-12):

Figure 22-12 Tension et courant dans un circuit inductif

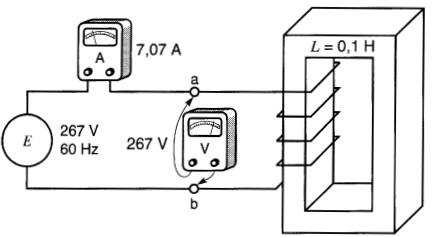
I_eff = 7,07A (ou 0,707 X 10A)

E_eff = 267V (ou 0,707 x 377V)

On peut démontrer que la réactance inductive d'une bobine est donnée par la formule :

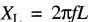    (22-7)

ou

X_L = réactance inductive, en ohms [Ω]

f = fréquence de la source, en hertz [Hz]

L = inductance de la bobine, en henrys [H]

π = 3,1416

Ainsi, dans l'exemple précédent, la valeur de XL pour l'inductance de 0,1 H à une fréquence de 60 Hz est :

X_L = 2πfL = 2 x 3,14 x 60 x 0,1 = 37,7Ω

La formule 22-7 indique que la réactance inductive d'une bobine est proportionnelle à son inductance et à la fréquence de la source. Donc, une bobine s'oppose d'autant plus au passage d'un courant que son inductance est plus grande et que la fréquence est plus élevée.

Exemple 22-4

Une bobine ayant une inductance de 2 H est raccordée à une source de 100V efficace dont la fréquence est de 60 Hz.

La résistance de la bobine (déterminée par un ohmmètre) est négligeable.

Calculer le courant qui la parcourt.

Solution

Déterminons d'abord la réactance inductive de la bobine.

X_L = 2πfL = 2 x 3,14 x 60 x 2 = 754Ω

On en déduit le courant:

I = E/X_L = 100V / 754Ω = 0,133A (efficace)

Puissance réactive dans une bobine: le var inductif

Nous avons retracé à la Fig. 22-13 les courbes de tension et de courant du montage de la Fig. 22-12.

Figure 22-13 La valeur moyenne de la puissance fournie à une inductance est nulle

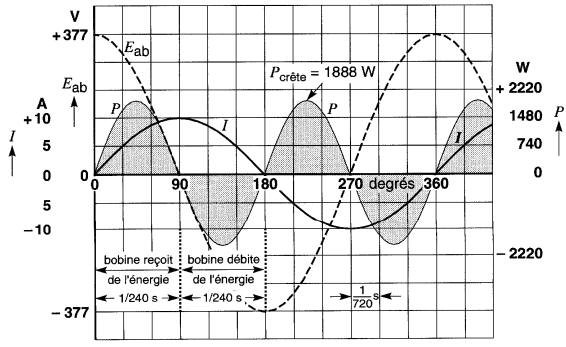
Si l'on applique la même méthode d'analyse que celle employée dans le cas du condensateur, on trouve que pendant le premier quart de cycle la puissance est positive (Fig. 22-13), et que la bobine reçoit de l'énergie de la source.

Par exemple, à 60° :

E_ab = +188,5V     I = +8,66A

d'où P = (+188,5V) x (+8,66A) = +1632W

Pendant le quart de cycle suivant, la puissance est négative : la bobine renvoie à la source l'énergie qu'elle dent d'accumuler dans son champ magnétique .

Il y a donc un échange continuel d'énergie entre la source et la bobine, de sorte que la bobine n'absorbe en moyenne aucune énergie.

Comme dans le cas du condensateur, la valeur moyenne de la puissance fournie par la source est nulle. Le produit de la valeur efficace du courant traversant une bobine par la valeur efficace de la tension à ses bornes porte le nom de puissance réactive inductive svmbole Q_L).

L'unité de puissance réactive inductive est le volt-ampère réactif (symbole var). La puissance réactive fournie à la bobine de la Fig. 22-11 est:

Q_L = E_eff x I_eff = 267V x 7,07A = 1888 var

La Fig. 22-14 montre une application importante des réactances inductives.

Figure 22-14 Groupe de 6 bobines ayant chacune une réactance inductive de 1,2Ω à 60 Hz. Ces réactances, installées en série avec des lignes à 14,4 kV au poste de transformation La Suète à Sainte-Foy, limitent le courant de court-circuit à une valeur maximale de 12 000 A.

Exemple 22-5

Une inductance de 0,2H est reliée à une source de 110V ayant une fréquence de 60 Hz.

Calculer: a) la réactance inductive de la bobine b) le courant efficace c) la puissance réactive absorbée par la bobine

Solution

a) La réactance inductive est:

X_L = 2πfL = 2 x 3,14 x 60 x 0,2 = 75,4Ω

b) le courant efficace dans la bobine est:

I = E/X_L = 100V / 75,4Ω = 1,46A

c) la puissance réactive inductive est :

Q_L = EI = 110 x 1,46 = 160 var

Comparaison entre les circuits R, L et C

La plupart des circuits électriques sont composés essentiellement de l'un ou d'une combinaison des trois éléments suivants:

la résistance R, la capacitance C et l'inductance L.

Le comportement de chacun de ces trois éléments dans un circuit à courant alternatif est résumé dans le tableau 22-1.

Valeur moyenne d'un courant ou d'une tension périodique

Il arrive dans les montages d'électronique de puissance que les tensions et les courants aient des formes d'ondes non sinusoïdales. Nous présentons maintenant une méthode permettant de déterminer facilement la valeur moyenne et la valeur efficace de ces formes d'ondes spéciales.

Nous choisirons une onde de courant périodique, sachant que les mêmes remarques s'appliquent à une onde de tension périodique. Le cycle d'un courant périodique peut être subdivisé en une série d'intervalles de durées plus ou moins courtes durant lesquels le courant suit essentiellement une ligne droite.

À chaque intervalle, le courant possède une valeur initiale a et une valeur finale b. La valeur moyenne du courant durant un intervalle est donc:

valeur moyenne = M = (a + b)/2

Si la durée de l'intervalle, mesurée en secondes, est Δt, la surface élémentaire ΔS_M associée à cet intervalle est:

ΔS_M = M x Δt

La surface totale durant un cycle est obtenue en additionnant les surfaces élémentaires. Nous la désignerons par le symbole S_M.

Connaissant la période T du cycle, la valeur moyenne du courant périodique est donnée par l'expression:

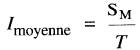    (22-8)

La valeur moyenne ainsi trouvée correspond à la composante à c.c. du courant analysé. Habituellement, pour les ondes périodiques, le temps est exprimé en degrés plutôt qu'en secondes.

La durée des intervalles est également exprimée en degrés (Δθ). Puisque la période T correspond à 360°, la valeur moyenne du courant est donnée par l'expression:

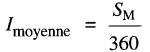    (22-9)

où

I moyenne = valeur moyenne du courant ou composante à c.c.

S_M = surface totale correspondant à un cycle, calculée en ampères-degrés

360 = nombre de degrés dans un cycle

Valeur efficace d'un courant ou d'une tension périodique

Pour calculer la valeur efficace d'un courant périodique, on subdivise le cycle de la même manière que dans la section précédente. On identifie encore par a et b les valeurs du courant au début et à la fin de chaque intervalle.

Cependant, on peut montrer que la valeur moyenne à utiliser durant un intervalle est maintenant donnée par

(a² + b² + ab)/3 au lieu de (a + b)/2.

On peut donc écrire:

N = (a² + b² + ab)/3

oÙ N est la valeur moyenne des carres durant l'intervalle. Si la durée de l'intervalle, mesurée en degrés, est Δθ, la surface élémentaire ΔS_N associée à cet intervalle est donc:

ΔS_N = N x Δθ   

La surface totale durant un cycle est obtenue en additionnant les surfaces élémentaires. Nous la désignons par le symbole S_N.

Par définition, la valeur efficace du courant est alors donnée par l'expression:

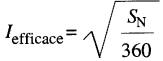    (22-10)

ou

I_efficace = valeur efficace du courant

S_N = surface totale correspondant à un cycle, calculée en ampères carrés-degrés

360 = nombre de degrés dans un cycle

Exemple illustratif 22-6

La Fig. 22-15 montre la forme d'onde d'un courant périodique durant un cycle.

Figure 22-15 Un cycle d'un courant non sinusoïdal

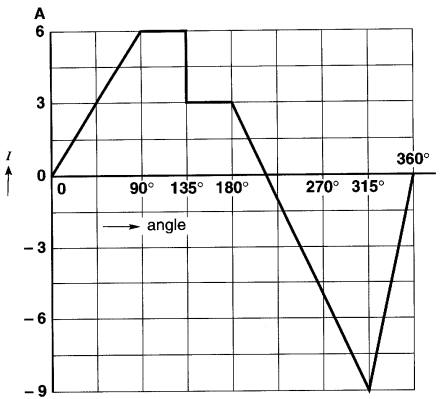
Nous avons choisi une forme d*onde spéciale afin de bien illustrer le calcul des valeurs moyenne et efficace. Le tableau 22-2 indique les valeurs du courant et de l'angle pour chaque intervalle, et les différentes étapes du calcul.

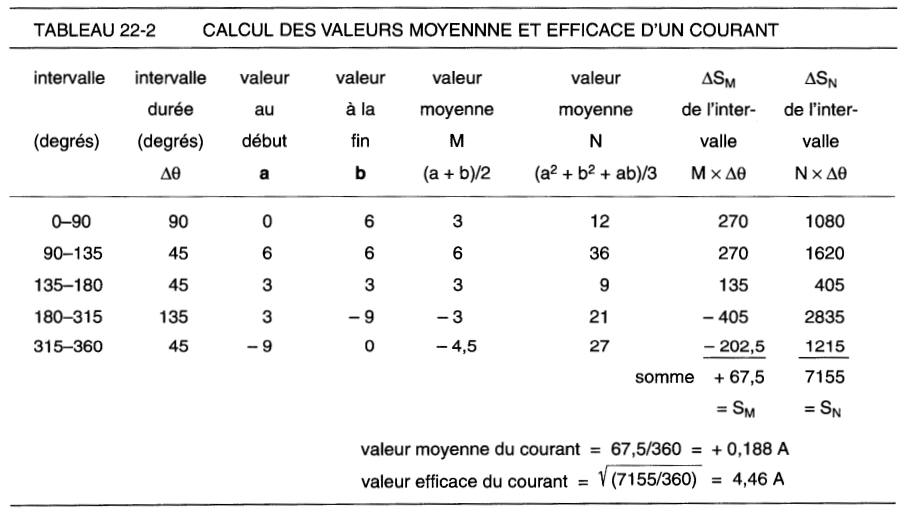
Par exemple, durant l'intervalle de 180° à 315°, on constate sur la Fig. 22-15, que la valeur initiale a = +3 et la valeur finale b = -9.

Par conséquent, la valeur moyenne M est:

M = (a + b)/2 = (+3 - 9)/2 = -3

La durée de l'intervalle est

315-180=135°

La surface élémentaire associée à cet intervalle est donc

ΔS_M = -3 x 135 = -405

De même, la valeur moyenne des carrés N est donnée par:

N = [(+3)² + (-9)² + (3) (-9)]/3 = 21

La surface élémentaire associée à cet intervalle est :

ΔS_N = 21 x 135 = 2835

Le tableau indique que la valeur moyenne du courant est +0,188A et que sa valeur efficace est 4,46A . C'est dire qu'un courant continu de 4,46A produira dans une résistance quelconque la même dissipation de chaleur que l'onde alternative de la Fig . 22-15.

Il est entendu que la même méthodologie peut servir pour calculer les valeurs moyenne et efficace d'une tension ou de toute autre grandeur.

Temps, fréquence et l'angle θ

Dans la section ci-haut nous avons indiqué que la tension d'une onde sinusoïdale peut être exprimée par l'équation:

e = E_M sinθ     éq. 22-1

dans laquelle l'angle θ est exprimé en degrés.

Une formule semblable a été donnée pour le courant, soit:

i = I_M sinθ     éq. 22-2

Or, on peut démontrer que l'angle θ est une fonction de la fréquence et du temps, soit:

θ = 360fT    (22-11)

où

θ = angle de rotation [degrés]

f = fréquence [Hz]

t = temps [s]

360 = constante tenant compte des unités

Exemple 22-7

Un courant sinusoïdal possède une valeur crête de 140A et une fréquence de 60 Hz . Sachant que sa valeur initiale est nulle et croît vers les valeurs positives, déterminer sa valeur après un intervalle de 93 ms.

Solution

L' angle θ correspondant au temps et à la fréquence est

θ = 360ft = 360 x 60 x 0,093 = 2008,8 degrés

La valeur du courant à cet instant est donc :

i = I_m sin θ = 140 sin 2008,8° = 140 x (- 0,482) = -67,4 A

Expressions généralisées d'une tension sinusoïdale

Une tension de forme d'onde sinusoïdale peut avoir une valeur initiale qui n'est pas nulle. De plus, au départ, elle peut croître ou décroître.

Dans ces circonstances, on peut décrire sa forme d'onde de deux façons:

1) par l'expression générale en fonction de l'angle θ :

e = E_m sin (θ + α)     (22-12)

2) par l'expression générale en fonction du temps t :

e = E_m sin (360ft + α)     (22-13)

où

e = valeur instantanée de la tension [V]

E_m = valeur crête de la tension sinusoïdale [V]

θ = angle exécuté à partir de t = 0, en degrés [°]

α = angle de départ, en degrés [°]

f = fréquence, en hertz [Hz]

t = temps, en secondes [s]

De ces deux équations, à moins d'être obligé de faire intervenir le temps t, on préfère utiliser l'équation (22-12) qui exprime la tension en fonction de l'angle de rotation θ.

Exemple 22-8

Une tension sinusoïdale E_ab entre deux bornes a et b possède une valeur crête de 200V et l'angle de départ α est de - 32 degrés.

Déterminer. pour les angles θ compris entre zéro et 900 degrés :

a) la valeur initiale de la tension

b) les angles θ où la tension E_ab passe par des valeurs nulles

c) les angles θ où la tension E_ab passe par des valeurs maximales positives

d) les angles θ où la tension E_ab passe par des valeurs maximales négatives

e) Faire un schéma. à main levée, montrant la forme d'oncle de la tension E_ab entre θ= 0° et θ= 900°

Solution

a) La valeur initiale de E_ab correspond à θ = 0, ce qui donne E_ab = 200 sin (0 - 32) = - 106V

b) La valeur de Eab est nulle lorsque sin (θ + α) = 0, soit lorsque (θ- 32) = 0, 180, 360, 540, 720 et 900 degrés.
Cela correspond à θ = 32, 212, 392, 572, 752 et 932 degrés.

c) La valeur de E_ab est maximum positive lorsque sin (θ + α) = + 1, soit lorsque (θ- 32) = 90, 450 et 810 degrés.
Cela correspond à θ = 122, 482 et 842 degrés

d) La valeur de E_ab est maximum négative lorsque sin (θ + α) = - 1, soit lorsque (θ - 32) = 270, 630, 990 degrés.
Cela correspond à θ= 302, 662 et 1022 degrés.

 e) Il suffit de tracer sur papier quadrillé les points de repère (E_ab et θ) trouvés dans les parties a) à d) et de les relier par une courbe ayant une allure sinusoïdale. Voir Fig 22-16.

Figure 22-16 Tension sinusoïdale en fonction de l'angle 6

Exemple 22-9

Une tension sinusoïdale E_ab, possède une valeur crête de 200V et une fréquence de 9.1 Hz . Sa valeur initiale correspond à un angle ade-32°.

Déterminer

a) la valeur initiale de la tension

b) la valeur de la tension après un intervalle de 160 ms

c) tracer la l'orme d'onde de la tension entre t = 0 et t = 240 ms.

Solution

a) En se référant à l'équation (22-13) on a E_m = 200V et t = 0. Sachant que α =-32°, on peut écrire:

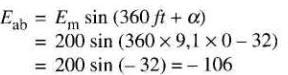
soit E_ab = - 106 V

b) En se référant de nouveau à l'équation (22-13) on a E_m = 200V, t = 0,16 s et α est toujours de - 32°.

On peut donc écrire:

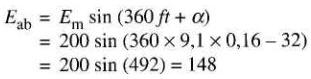
soit E_ab = 148V

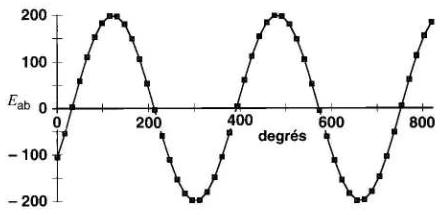
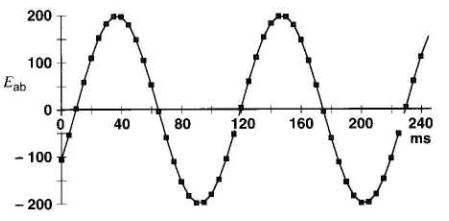
c) En utilisant un ordinateur, on trouve la forme d'onde de la tension E_ab en fonction du temps t (Fig. 22-17). La même forme d'onde en fonction de l'angle θ est présentée à la Fig. 22-16.

Figure 22-17 Tension sinusoïdale en fonction du temps t

Expressions avec angles en radians

Dans certains cas, on préfère utiliser le radian au lieu du degré comme unité d'angle de rotation. Dans ces circonstances, les équations suivantes s'appliquent :

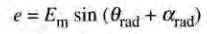
soit:

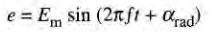    (22-13)

où

α_rad = angle de départ (à t = 0)

f = fréquence [Hz]

t = temps [s]

2π = constante tenant compte des unités

Le fait d'exprimer l'angle de rotation en radians au lieu d'en degrés ne change rien à la valeur de la tension instantanée. Cela revient à changer l'unité de mesure, comme par exemple, exprimer une longueur en arpents au lieu qu'en mètres. Des expressions analogues s'appliquent aux courants sinusoïdaux.

Résumé

Dans cette section nous avons défini plusieurs grandeurs que nous utiliserons constamment dans les circuits à courant alternatif. Pour une tension ou un courant sinusoïdal nous utiliserons la valeur efficace plutôt que la valeur crête.

Nous avons vu qu'en régime sinusoïdal, à une fréquence donnée, la bobine et le condensateur possèdent une certaine réactance mesurée en ohms.

La réactance inductive et la réactance capacitive donnent la relation entre la tension et le courant efficace d'une inductance et d'une capacitance tout comme la résistance dans la loi d'Ohm.

Pour une résistance, la tension et le courant sont en phase. Pour une inductance, le courant est déphasé de 90 degrés en arrière de la tension. Pour une capacitance le courant est déphasé de 90 degrés en avant de la tension.

Pour chacun des éléments: résistance, inductance et capacitance, la puissance est obtenue en faisant le produit de la tension efficace et du courant efficace. Pour la résistance, il s'agit d'une puissance active mesurée en watts correspondant à un dégagement de chaleur.

Par contre, pour un élément comme une inductance ou une capacitance, il s'agit 'une puissance réactive mesurée en vars qui ne donne lieu à aucun échauffement mais seulement à un échange d'énergie entre l'élément et le reste du circuit.

Enfin, nous avons présenté une méthode de calcul simple pour trouver la valeur moyenne et la valeur efficace d'une tension ou d'un courant périodique non sinusoïdal.

PROBLÈMES

Niveau pratique

22-1 Que veut dire l'énoncé suivant: le courant dans une résistance est en phase avec la tension?

22-2 La valeur moyenne de la puissance dissipée dans la résistance d'un circuit à c .a. est-elle égale au produit de la valeur crête de la tension et de la valeur crête du courant?

22-3 Qu'entend-on par valeur efficace d'une tension sinusoïdale?

22-4 Qu'est-ce que la réactance d'un condensateur? Par quelle unité l'exprime-t-on? Augmente-t-elle si la fréquence augmente?

22-5 Quelle est la valeur moyenne de la puissance dissipée dans un condensateur?

22-6 Qu'entend-on par puissance réactive? Quelle est son unité?

22-7 Le courant dans une bobine est-il en phase avec la tension? Si non, est-il en avant ou en arrière de celle-ci?

22-8 La réactance inductive d'une bobine diminue-t-elle si la fréquence diminue?

22-9 Dans un circuit à c.a. une bobine agit tantôt comme une source, tantôt comme une charge. Expliquer.

22-10 Quelle est la valeur efficace d'une tension sinusoïdale dont la valeur crête est de 120V?

22-11 Dans un circuit à c.a., un ampèremètre indique un courant de 10A. Calculer la valeur crête de ce courant sinusoïdal.

22-12 L'enroulement d'un transformateur possède une réactance inductive de 1000 S2 à 60 Hz. Que devient-elle à 25 Hz?

22-13 Tracer la forme d'onde d'une tension sinusoïdale dont la valeur crête est de 180 V.

Niveau intermédiaire

22-14 Une tension sinusoïdale de 60 Hz, 100V (efficace) appliquée à un condensateur fait circuler un courant de 20 A (efficace). Déterminer la réactance capacitive de ce condensateur. Que deviendrait cette réactance si la fréquence de la source doublait?

22-15 Quelle est la valeur de la réactance capacitive d'un condensateur de 0,05 µF à une fréquence de 1000 Hz?

22-16 Un condensateur de 3 µF est raccordé à une source de tension de 63V, 1000 Hz.

Calculer:

a) la valeur de la réactance capacitive du condensateur à cette fréquence

b) la valeur efficace du courant

c) la valeur de la puissance active fournie au condensateur

d) la valeur de la puissance réactive

22-17 Une bobine de 2H dont la résistance est négligeable est raccordée à une source de 110V, 60 Hz . Quel courant y circule? Quelle est la valeur de la puissance réactive mise en jeu?

22-18 Dans la Fig. 22-10 les condensateurs sont raccordés en parallèle. Calculer pour chaque condensateur:

a) la puissance réactive en kvars

b) le courant efficace

c) la réactance capacitive

d) la capacitance, en microfarads

e) l'énergie crête emmagasinée, en joules

f) la puissance active instantanée maximale que le condensateur débite, en watts

22-19 Calculer l'inductance de chaque bobine de la Fig. 22-14.

22-20 Une réactance inductive de 110 Mvar est installée sur un réseau à 60 Hz.

Calculer: 

a) le courant efficace absorbé par la réactance sachant que la tension appliquée est de 424 kV

b) l'inductance et l'énergie maximale emmagasinée dans le champ magnétique

22-21 En se référant à la Fig. 22-9, faire sept schémas montrant la valeur et le sens du courant, de même que la valeur et la polarité de la tension aux bornes du condensateur à 30, 45, 60, 90, 135, 180 et 225 degrés.

Puis calculer la valeur de la puissance instantanée (en watts) dans chaque cas et indiquer si le condensateur reçoit ou débite de l'énergie.

Niveau avancé

22-22 Une source spéciale produit la forme d'onde de tension périodique illustrée à la Fig. 22-18.

Figure 22-18 Voir problème 22-22

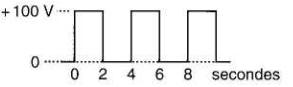
Si cette tension est appliquée sur une résistance de 10Ω calculer:

a) la fréquence de la tension

b) la puissance crête

c) l'énergie dissipée par cycle

d) la puissance moyenne par cycle

e) la tension continue qui donnerait la même puissance moyenne f) la valeur efficace de la tension de la source

22-23 Répéter les calculs du problème 22-22pour la forme d'onde de la Fig. 22-19.

Figure 22-19 Voir problème 22-23

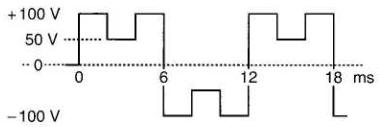
22-24 Répéter les calculs du problème 22-22 pour la forme d'onde de la Fig. 22-20.

Figure 22-20 Voir problème 22-24

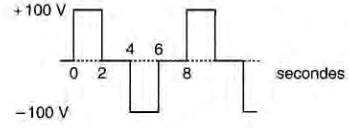
22-25 Un courant sinusoïdal de 60 Hz atteint une valeur crête de 100 A. Quel est le taux de variation maximal de ce courant, et à quel moment ce taux est-il atteint?

22-26 Prouver que si un courant sinusoïdal a une valeur crête I_m, son taux de variation maximal peut être exprimé par la formule 360f sin 1° I_m, où f est la fréquence.

22-27 Une ligne de transport monophasée a les caractéristiques suivantes:

type de conducteur: #2/0 en cuivre, toronné,

diamètre 10,5 mm

distance entre les conducteurs : 2,5 m

longueur de la ligne: 60 km

tension et fréquence de la source: 69 kV, 60 Hz

Calculer:

a) la capacitance de la ligne et le courant circulant dans celle-ci à circuit ouvert

b) la puissance réactive capacitive de la ligne

c) la tension crête entre les conducteurs

22-28 Dans le problème 22-27, calculer l'énergie crête emmagasinée dans le champ électrique; à quel instant est-elle maximale?

22-29 La ligne du problème 22-27 alimente une charge où circule un courant de 50A. En négligeant l'effet capacitif de la ligne, calculer :

a) la réactance inductive de la ligne (section 19 .15)

b) la tension efficace induite par le champ magnétique

c) l'énergie crête emmagasinée dans le champ magnétique

22-30 Une inductance semblable à celle montrée à la Fig. 19-24 est composée de 2000 spires. La section du noyau est de 20 cm² et l'entrefer a une longueur de 3 mm. Calculer la réactance inductive à une fréquence:

a) de 60 Hz

b) de 180 Hz

22-31 Une bobine semblable à celle montrée à la Fig. 19-26 possède un diamètre de 150 mm et une longueur de 500 mm. Elle porte 60 spires de fil #10. Calculer la réactance inductive à une fréquence de 50 kHz .

22-32 On donne l'information suivante sur les barres omnibus de la Fig. 19-29:

a = 150 mm; b = 6 mm: D = 100 mm; l = 200 m.

La tension efficace entre les barres est de 600V, 60 Hz. Les barres portent un courant efficace de 1400 A.

Calculer:

a) l'inductance de la ligne

b) la réactance inductive de la ligne

c) la chute de tension due à la réactance

22-33 Une réactance d'artère de 2,2Ω, 500A a un diamètre moyen de 1,5 m et une hauteur de 1,2 m.

Sachant qu'elle est construite selon le modèle de la Fig. 19-26 et qu'elle fonctionne à 60 Hz, calculer:

a) l'inductance de la bobine

b) le nombre de spires

c) la section du conducteur en cuivre si l'on utilise une densité de courant de 2 ampères (efficace) par millimètre carré

d) le diamètre du conducteur

e) la résistance approximative de la bobine à 20 °C

Réponses

10)84,9V; 11) 14,1A; 12) 417Ω; 14) 5Ω; 2,5Ω; 15) 3183Ω;
16a) 53Ω; 16b) 1,19A; 16c) 0 W; 16d) 74,8 var; 17) 0,146A;
16 var; 18a) 150 kvar; 18b) 10,42A; 18c) 1382Ω; 18d) 1,92µF;
18e) 398 J; 18f) 150 kW; 19) 3,18 mH; 20a) 259A;
20b) 4,33 H; 291 kJ; 21) + 433 W; + 500 W; + 433 W; 0 W; -500 W;
0 W; + 500 W; (+) indique que le condensateur absorbe de
l'énergie; 22a) 0,25 Hz; 22b) 1000 W; 22c) 2000 J; 22d) 500 W;
22e) 70,7 V; 22f) 70,7 V; 23) 0,125 Hz; 1000 W; 4000 J; 500 W;
70,7 V; 70,7 V; 24) 83,3 Hz; 1000 W; 9 J; 750 W; 86,6 V; 86,6 V;
25) 37 700 A/s à t = 0 s; 27a) 0,269 µF; 7,0 A; 27b) 483 kvar;
27c) 97,6 kV; 28) 1281 J lorsque la tension est max.; 29a) 58Ω;
29b) 2,9 kV; 29c) 385 J; 30a) 1257Ω; 30b) 3771Ω; 31) 44,8 Ω;
32a) 84,3 pH; 32b) 31,8 mΩ; 32c) 44,5 V; 33a) 5,84 mH;
33b) 70 spires; 33c) 250 mm²; 33d) 17,8 mm; 33e) 22,7 mΩ