Circuits simples à courant continu

Électrotechnique

La plupart des circuits électriques sont raccordés soit en série, soit en parallèle, soit en série-parallèle. Dans cette section nous étudions ces trois types de circuits et comment on peut les résoudre.

Les circuits plus complexes et moins fréquents sont expliqués à la section Solutions des circuits à courant continu

Groupement en série Des appareils électriques sont raccordés en série lorsque la borne de l'un est connectée avec la borne du suivant, de façon à réaliser une chaîne.

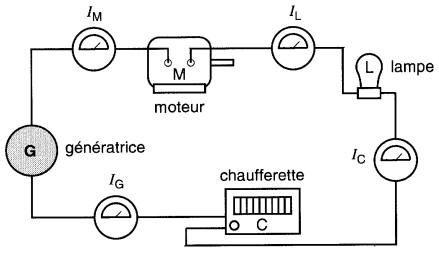
La Fig. 5-1a montre un circuit série formé d'une génératrice, d'un moteur, d'une lampe et d'une chaufferette. Les circuits séries possèdent trois propriétés principales:

1) Le courant est le même dans tous les éléments.

Figure 5-1a Groupement en série mesure des courants à l'aide d'ampèremètres

Dans la Fig. 5-1a, les courants sont tous égaux car les électrons ne peuvent pas quitter les conducteurs dans lesquels ils circulent. Par conséquent, les 4 ampèremètres donnent la même lecture.

I_moteur = I_lampe - I_chaufferette = I_{génératrice}

IM = IL = IC = IG

2) La somme des tensions aux bornes des charges est égale à la tension aux bornes de la source.

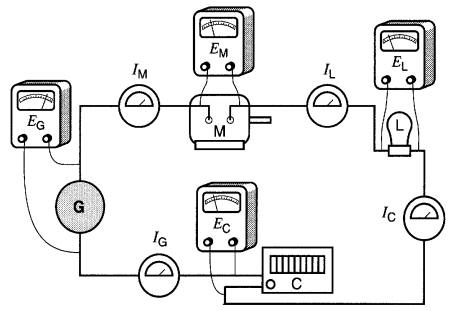
Dans la Fig. 5-1b on aura:

E_moteur + E_lampe + E_chaufferette =  E_{génératrice}

EM + EL + Ec = EG

Figure 5-1b Groupement en série - mesure des tensions à l'aide de voltmètres

3) La somme des puissances absorbées par les charges est égale à la puissance fournie par la source. C'est une conséquence de la loi de la conservation de l'énergie.

Étant donné que la puissance est égale au produit de la tension aux bornes d'un élément par le courant qui le traverse, on aura

P_moteur + P_lampe + P_chaufferette = P_{génératrice}

soit

E_MI_M + E_LI_L + E_CI_C = E_GI_G

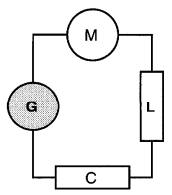
Ces trois règles s'appliquent à tout circuit série, quelle que soit la nature des charges. La Fig. 5-2 est une représentation schématique des quatre composants du circuit.

Figure 5-2 Diagramme schématique du montage de la Fig. 5-1

Groupement de résistances en série; résistance équivalente

Il arrive souvent que les charges dans un circuit série soient composées entièrement de résistances.

On peut démontrer que

1) La résistance de l'ensemble de ces résistances est égale à la somme des résistances individuelles.

On peut donc remplacer un groupe de résistances R1, R2, R3... Rn par une seule résistance équivalente Req qui tirerait le même courant de la source et qui dissiperait la même puissance.

Celle-ci serait donnée par

Req = =R1 +R, +R3 +....+Rn   (5-1)

Considérons les trois résistances connectées en série aux bornes d'une source de 220 V (Fig. 5-3a).

Figure 5-3 Résistances branchées en série

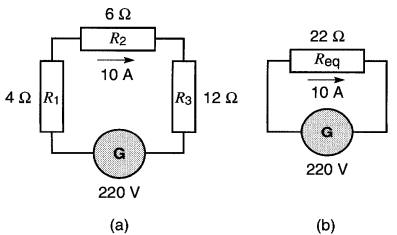
La résistance équivalente à l'ensemble de ces résistances sera donc

Req = 4 + 6+ 12 = 22Ω

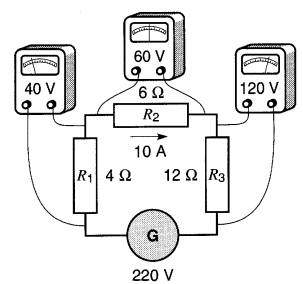
La tension de 220 V provoque dans ce montage un courant de

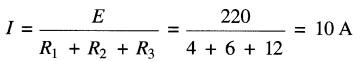
En utilisant la résistance équivalente (Fig. 5-3b) on trouve directement :

I = E / Req= 220 / 22 = 10 A

La puissance dépensée par effet Joule dans chacune des résistances a pour valeur P = RI.

dans R1 , P1 = 4 x (10)² = 400W

dans R2 , P2 = 6 x (10)² = 600W

dans R3 , P3 = 12 x (10)² = 1200 W

soit au total: 2200 W.

La puissance débitée dans la résistance équivalente a pour valeur:

P = 22 x (10)² = 2200 W

On vérifie donc que la résistance équivalente tire le même courant et dissipe la même puissance que l'ensemble des résistances.

Aussi, la somme des puissances dépensées dans les résistances est bien égale à la puissance débitée par la génératrice, soit

P = EI = 220 x 10 = 2200 W

2) La tension aux bornes de chacune des résistances est égale au produit de cette résistance par le courant qui traverse le circuit.

De plus, la différence de potentiel aux bornes de l'ensemble est égale à la somme des tensions individuelles aux bornes de chaque résistance.

Ainsi, pour le circuit considéré, la tension aux bornes de chaque résistance sera E= RI.

pour R1 , El = 4 x 10 = 40 V

pour R2, E2 = 6 x 10 = 60 V

pour R3, E3 = 12 x 10 = 120 V

soit au total : 220 V

Ainsi, la somme des tensions indiquées par les voltmètres aux bornes des trois résistances est égale à la tension aux bornes de la génératrice, soit 220 volts (Fig. 5-4).

Figure 5-4 Mesure des tensions aux bornes des résistances

Groupement en parallèle

Des appareils électriques sont raccordés en parallèle lorsque leurs bornes sont connectées aux deux mêmes points. La Fig. 5-5 montre un groupement parallèle formé d'un moteur, d'une lampe et d'une chaufferette branchés aux bornes A et B d'une génératrice.

Figure 5-5 Groupement en parallèle

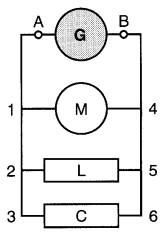
On suppose que les deux conducteurs partant de ces bornes possèdent une résistance négligeable.

Il s'ensuit que les points 1, 2 et 3 sont électriquement au même potentiel que la borne A. De la même façon, les points 4, 5 et 6 sont électriquement au même potentiel que la borne B.

Tout comme les circuits série, les circuits parallèle possèdent trois propriétés principales:

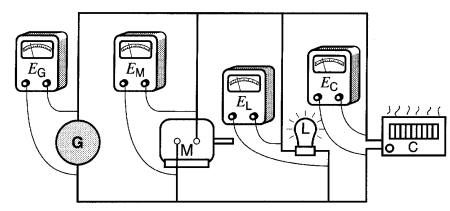
1) La tension est la même aux bornes de chaque élément. Sur le montage de la Fig. 5-6a, les quatre voltmètres donnent la même lecture

Figure 5-6a Groupement en parallèle - mesure des tensions aux bornes des éléments

E_moteur = E_lampe = E_chaufferette = E_{génératrice}

EM = EL = Ec = EG

2) La somme des courants tirés parles charges est égale au courant débité par la source.

Dans la Fig. 5-6b, les courants indiqués par les quatre ampèremètres donnent

I_moteur +I_lampe + I_chaufferette = I_{génératrice}

IM + IL + Ic = IG

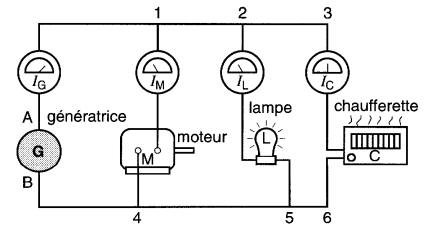
Figure 5-6b Groupement en parallèle - mesure des courants dans les éléments

Groupement de deux résistances en parallèle

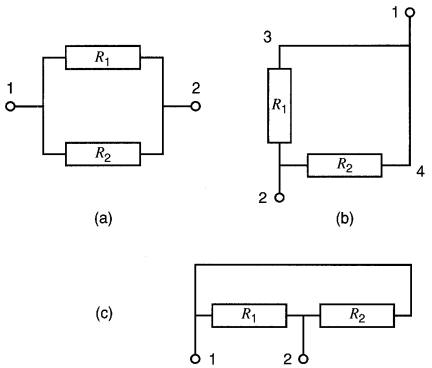
Chacun des montages de la Fig. 5-7 représente deux résistances R1 et R2 montées en parallèle car leurs extrémités sont reliées aux deux mêmes points 1 et 2.

Figure 5-7 Trois manières de grouper 2 résistances en parallèle

Considérons une batterie d'accumulateurs de 30 V alimentant une résistance R1 de 6 S2 (Fig. 5-8).

Figure 5-8 Batterie alimentant une résistance de 6 Ω

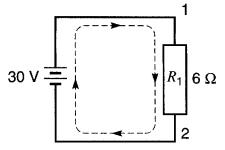
Pour une tension de 30 V entre ses bornes 1 et 2, la résistance tire un courant de 5 A de la source.

En effet, I = E / R = 30 / 6 = 5A

La circulation de ce courant ne change pas la tension entre les points 1 et 2; elle est encore de 30 V.

Si on raccorde maintenant à ces deux mêmes points une résistance R2 de 3Ω (montage parallèle, tel qu'indiqué à la Fig. 5-9), il circule un courant de 30 V/3Ω = 10A dans cette nouvelle résistance.

Figure 5-9 Courants lorsqu'une résistance de 3 S2 est ajoutée en parallèle avec celle de 6Ω

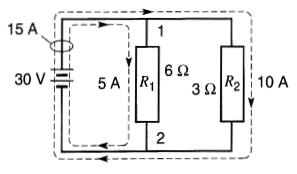
Comme ce courant vient de la même source, le courant total fourni par la batterie sera la somme des courants dans chacune des résistances, soit 5 A + 10 A = 15 A.

Si les deux résistances étaient cachées, un technicien mesurant une tension de 30 volts et un courant de 15 A en déduirait qu'une résistance de 30 V/15 A = 2Ω est branchée à la source.

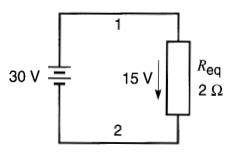
Donc, deux résistances de 6Ω et 3Ω branchées en parallèle produisent le même effet qu'une seule résistance de 2Ω (Fig. 5-10).

Figure 5-10 Circuit équivalent du montage de la figure 5-9

Montage en parallèle; résistance équivalente

Pour le groupement parallèle, on notera que la résistance unique équivalente à deux résistances en parallèle est égale au produit des résistances divisé par leur somme.

Ainsi la résistance Req de l'ensemble de deux résistances R1 et R2 en parallèle est donnée par la formule:

Req = R1R2 / (R1 + R2)    (5-2)

Exemple 5-1

Deux résistances (le 6Ω et 3Ω sont raccordées en parallèle (Fig. 5-9).

Calculer la valeur de la résistance équivalente.

Solution

D'après la formule, la résistance unique pouvant rem- placer les deux en parallèle a pour valeur:

Req = R1R2 / (R1 + R2) = 6x3 (6+3) = 18 / 9 = 2Ω

On constate que la valeur de la résistance équivalente (2Ω) est inférieure à la plus petite des résistances (3Ω).

Il est bon de se rappeler que le fait d'ajouter une deuxième résistance offre un nouveau passage au courant et, par suite, diminue la résistance offerte à la source.

Répartition du courant dans un groupement parallèle

La connaissance de la résistance équivalente nous aide à déterminer la répartition du courant entre deux résistances raccordées en parallèle.

Par exemple, lorsqu'on connaît le courant total alimentant deux résistances groupées en parallèle, on peut déterminer le courant dans chacune en appliquant la méthode suivante (voir Fig. 5-11):

Figure 5-11 Répartition du courant de ligne entre deux résistances en parallèle

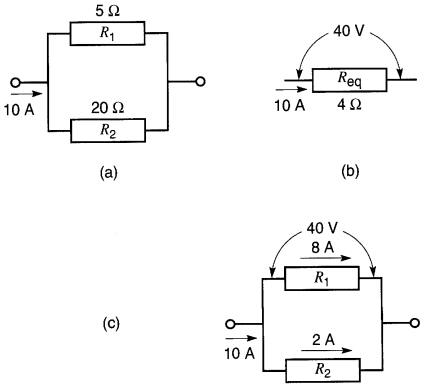
Dans cette figure, deux résistances de 5Ω et de 20Ω sont alimentées par un courant de 10 A.

Calculons le courant circulant dans chacune.

a) on détermine tout d'abord la valeur de la résistance équivalente:

Rreg = 5x20 / (5 + 20) = 4Ω

b) on calcule la chute de tension dans la résistance équivalente

E = RI = 10 x 4 = 40V

La tension commune aux deux résistances en parallèle est donc de 40 V

c) une fois que la tension commune des résistances est connue, il est facile d'établir le courant circulant dans chacune d'elles.

Ainsi, dans la résistance de 5Ω:

I = 40 V / 5Ω = 8A 

et dans la résistance de 20Ω:

I = 40 V /  20Ω = 2A

soit au total : 8A + 2A = 10A

L'intensité du courant est évidemment plus grande dans la plus basse résistance.

Court-circuit

Soit une résistance RI parcourue par un courant.

Si on dispose en parallèle avec celle-ci une deuxième résistance R2 constituée par un conducteur de forte section, on dira que la résistance RI est court-circuitée par la résistance R2 (Fig. 5-12).

Figure 5-12 Court-circuit de la résistance R1

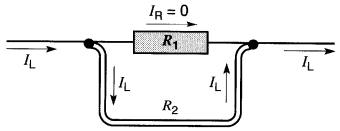
R2 ayant une résistance pratiquement nulle, elle sera parcourue par tout le courant ; il ne passera qu'un courant négligeable dans la résistance RI mise en court-circuit.

Groupement de trois ou plusieurs résistances en parallèle

Pour trouver la résistance équivalente d'un ensemble de trois résistances, on procède comme suit (voir Fig. 5-13):

Figure 5-13 Groupement parallèle de trois résistances

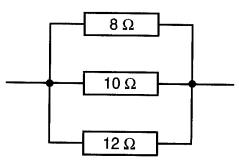
a) on trouve la résistance équivalente de deux des résistances, soit:

R = 8 x 10  / (8 + 10) = 4,44Ω

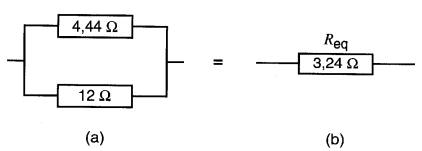
b) on calcule ensuite la résistance équivalente de la combinaison parallèle de la troisième résistance avec la résistance équivalente déjà calculée:

R = 4,44 x 12 / (4,44 + 12) = 3,24Ω

Les schémas de la Fig. 5-14 indiquent clairement les étapes que nous avons suivies.

Figure 5-14 Réduction progressive du circuit de la figure 5-13

On procédera de la même façon pour trouver la résistance équivalente à plus de trois résistances en parallèle.

Cas particulier :

La résistance équivalente à n résistances R identiques en parallèle est égale à Rln.

Par exemple, la résistance équivalente à 7 résistances de 21Ω en parallèle est de 21Ω / 7 = 3Ω.

Conductance

L'inverse de la résistance s'appelle conductance.

Ainsi, une résistance de 25Ω possède une conductance de 1/(25Ω).

L'unité SI de conductance est le siemens (symbole S) et 1 siemens = 1/ohm.

Une résistance de 25Ω a donc une conductance de 1/25 siemens, ou 0,04S.

La conductance G d'un groupe de résistances en parallèle est égale à la somme des conductances de chacune.

Soit un groupe de résistances RI, R2, R3,... Rn branchées en parallèle dont la résistance équivalente est Req.

Puisque la conductance G du groupe est égale à la somme de leurs conductances individuelles, et que G = 1/Req, il s'ensuit que:

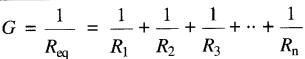  (5-3)

Exemple 5-2 Soit cinq résistances de 10. 20, 30, 40 et 50Ω branchées en parallèle.

Calculer leur conductance et la valeur de leur résistance équivalente.

Solution

La conductance G du groupe est:

G=1/10 + 1/20 + 1/30 + 1/40 + 1/50 = 0,228 siemens = 0,228S

Il s'ensuit que la résistance équivalente est

Req = 1 / 0,228S = 4,38Ω

Groupement série-parallèle

Les groupements série-parallèle sont des groupements mixtes.

Pour résoudre de tels circuits on remplace les résistances en parallèle par leur résistance équivalente, et les résistances en série également par leur résistance équivalente.

Enfin on trouve la résistance qui peut remplacer cet ensemble de résistances équivalentes.

L'exemple numérique suivant illustre cette méthodologie.

Exemple 5-3

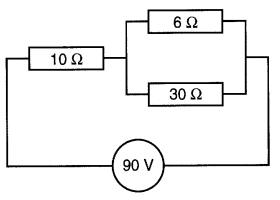
Trouver la puissance dissipée dans chacune des résistances de la Fig. 15

Figure 5-15

Solution

Il s'agit d'abord de trouver la résistance équivalente des résistances de 6Ω et 30Ω en parallèle.

R = 6 x 30 /(6 + 30) = 180 /  36 = 5Ω

Le circuit se réduit à celui de la Fig. 5-16.

Fig. 5-16

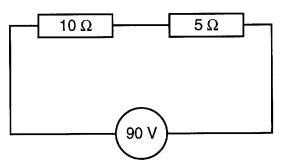
La résistance équivalente des résistances de 10Ω et 5Ω disposées en série sera:

R = R1 + R2 = 10 + 5 = 15Ω

Le groupe mixte des trois résistances est donc finalement remplacé par une seule résistance (Fig. 5-17).

Fig. 5-17

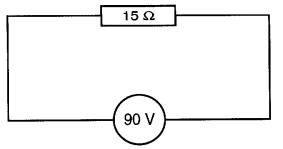
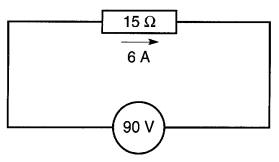
On procède maintenant par la méthode inverse pour trouver le courant et la tension de chacun des éléments (Fig. 5-18, 5-19 et 5-20).

Fig. 5-18	Fig. 5-19	Fig. 5-20

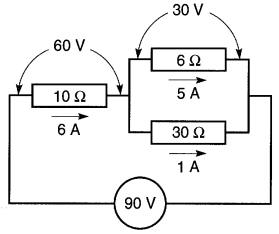Le courant débité par la source de 90 V, sera:

I= E / R = 90 / 15 = 6A

La résistance de 15Ω de la Fig. 5-18 est, nous l'avons vu, la résistance équivalente aux résistances de 10Ωet de 5Ω en série; le courant sera donc le même dans chacune de ces résistances (Fig. 5-19).

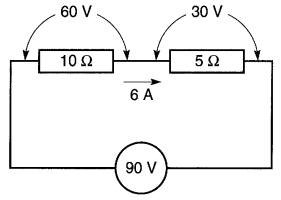
Les tensions aux bornes des résistances de 10Ωet 5Ω seront respectivement:

E = RI

E1 = 10 x 6 = 60V et E2 = 5 x 6 = 30 V

soit au total : 60V + 30V = 90V

On vérifie que la somme de ces tensions est bien égale à la d.d.p. aux bornes de la génératrice.

Maintenant, on remarque que la résistance de 5Ω remplace les résistances de 6Ωet de 30Ω en parallèle.

La tension aux bornes de ces dernières sera donc égale à celle aux bornes de la résistance de 5Ω, soit 30 volts (Fig. 5-20).

La tension commune aux résistances de 6Ω et de 30Ω étant de 30 volts, le courant dans chacun de ces éléments sera respectivement:

I1 = 30/6 =5A et I2 = 30/30 =1A

soit au total : 5 A + 1 A = 6 A

Connaissant les courants dans chacune des résistances, on peut trouver les puissances dissipées par chacune d'elles en utilisant:

 P = RI²

P résistance de 10Ω : 10 x (6)² = 360W

P résistance de 6Ω: 6 x (5)² = 150W

P résistance de 30Ω: 30 x (1)² = 30W

soit au total : 360W + 150W + 30W = 540W

On vérifie que la puissance débitée par la génératrice est égale à la somme des puissances dissipées dans chacune des résistances.

P = EI = 90 x 6 = 540 W

Résumé Dans ce chapitre nous avons appris à résoudre les circuits simples comprenant les deux raccordements de base :

la connexion série et la connexion parallèle

Dans un circuit série, le courant qui traverse les différents éléments est le même.

La tension apparaissant aux bornes de l'ensemble est la somme des tensions individuelles de chaque élément. De plus, la résistance équivalente d'un groupement de résistances connectées en série est la somme des résistances individuel-les, soit:

Req =R1 +R2 +...+Rn

Dans un circuit parallèle, la tension appliquée aux différents éléments est la même. Le courant circulant dans l'ensemble est la somme des courants individuels circulant dans chaque élément.

Pour des résistances branchées en parallèle, il est commode de définir la conductance G = 1/R. L'unité de conductance est le siemens.

La conductance d'un groupement de résistances connectées en parallèle est la somme des conductances individuelles, soit:

1/Req = 1/R1 + 1/R2 +...+ 1/Rn

Dans le cas particulier de 2 résistances branchées en parallèle on a:

Req = R1R2 / (R1 + R2)

L'utilisation des lois mentionnées ci-dessus permet de trouver les courants, tensions et puissances dans chacune des branches d'un circuit simple comprenant des groupements série-parallèle.

PROBLÈMES

Niveau pratique

5-1 Trouver la résistance équivalente à l'ensemble de deux résistances de 25Ω et de 82Ωdisposées en série.

5-2 Trois résistances respectivement égales à 6Ω, 5Ω et 9Ω sont groupées en série.

Calculer leur résistance équivalente.

5-3 Dans un montage série, tous les éléments portent le même courant. Expliquer.

5-4 Dans la Fig. 5-7b, si la tension entre les points 1 et 2 est de 40 V, quelle est la tension entre les points 3-4 ?

entre les points 2-4 ?

5-5 Dans un groupement de résistances en série, la même tension est-elle commune à toutes les résistances ?

Le même courant ?

5-6 Dans un groupement de résistances en parallèle, la même tension est-elle commune à toutes les résistances ?

Le même courant ?

5-7 On désire introduire une résistance additionnelle de 2,5 S2 dans un circuit afin de limiter l'intensité de courant.

Si on ne dispose que de résistances de 20Ω, combien faudra-t-il en disposer en parallèle ?

5-8 Trouver la résistance équivalente à l'ensemble de deux résistances de 45Ω et de 15Ω disposées en parallèle.

5-9 Une résistance de 25Ω est connectée en série avec la bobine d'un relais dont la résistance est de 80Ω.

Si une tension de 50 volts est appliquée à cet ensemble, quel sera le courant dans la bobine ?

Quelle sera la puissance dissipée dans la résistance de 25 S2 ?

Niveau intermédiaire

5-10 Un groupe de deux résistances de 20Ω et 30Ω disposées en série est raccordé à une source de 150 V.

Quelle tension mesurera-t-on aux bornes de la résistance de 30 S2 ?

Quelle sera la puissance débitée par la source ?

5-11 Si deux résistances de 20Ω et 30Ω sont groupées en parallèle, déterminer la résistance équivalente à l'ensemble.

Sachant qu'elles sont alimentées par une source de 150 V, calculer le courant tiré de celle-ci.

5-12 Un circuit parcouru par un courant de 18 ampères se divise en deux branches parallèles dont les résistances sont respectivement 4Ω et 5Ω.

Calculer la tension aux bornes des résistances ainsi que la répartition du courant dans les branches.

5-13 Calculer la résistance équivalente à trois résistances de 25Ω, 50Ω et 60Ω en parallèle.

5-14 Deux résistances de 25Ω et 40Ωsont disposées en série dans un circuit.

Sachant que la tension aux bornes de la résistance de 40Ω est de 50 volts, déterminer la tension aux bornes du circuit.

Calculer la puissance dissipée dans la résistance de 25Ω.

5-15 Deux résistances A et B sont connectées en série et alimentées par une génératrice sous une tension de 75 volts.

Si la tension aux bornes de la résistance A est de 40 volts et si un courant de 2 ampères circule dans le circuit, déterminer la valeur de la résistance B.

5-16 On utilise 16 isolateurs en porcelaine entre une ligne à 132 kV et un poteau en bois.

Calculer la valeur de la tension moyenne aux bornes de chaque isolateur.

Niveau avancé

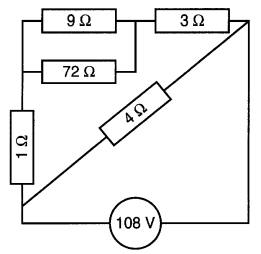
5-17 Le circuit donné à la Fig. 5-21 est raccordé à une génératrice dont la tension est de 108 V.

Trouver le courant et la tension pour chacun des éléments du circuit.

Figure 5-21 Voir problème 5-17

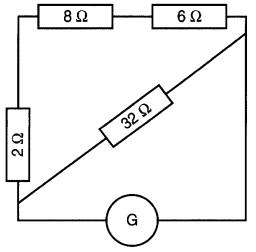
5-18 Dans la Fig. 5-22, la résistance de 32Ω dissipe une puissance de 1152 W.

Déterminer la valeur de la tension aux bornes de chaque élément.

Figure 5-22 Voir problème 5-18