Circuits triphasés

Électrotechnique

Jusqu'à maintenant, nous avons étudié le transport et l'utilisation de l'énergie électrique dans les circuits à courant continu et dans les circuits à courant alternatif alimentés par une seule source. Comme ils ne contiennent qu'une source et deux lignes d'alimentation, ces circuits sont appelés circuits monophasés.

Cependant, l'énergie électrique est distribuée à la plupart des installations industrielles par un système triphasé, composé de trois lignes. Les tensions alternatives entre les lignes ont même valeur et même fréquence, mais elles sont déphasées l'une par rapport à l'autre. Pour une puissance donnée, une ligne de transport triphasée demande moins de cuivre (ou d'aluminium) qu'une ligne monophasée de même tension.

De plus, les moteurs et les alternateurs triphasés sont plus petits, plus simples et moins coûteux que les moteurs et les alternateurs monophasés de même capacité, de même tension et de même vitesse. On peut comprendre l'avantage du système triphasé en le comparant à un simple moteur à essence.

Un moteur ayant un seul cylindre peut être assimilé à une machine monophasée. De même, un moteur à deux cylindres peut se comparer à une machine électrique diphasée. Enfin, un moteur à six cylindres peut être considéré comme un moteur à six phases.

Dans un tel moteur, des pistons identiques montent et descendent à l'intérieur de cylindres identiques, mais pas en même temps. Ils sont en effet reliés à l'arbre de façon à lui fournir des impulsions de puissance séquentielles, plutôt que simultanées. Il en résulte un moteur qui tourne plus doucement, avec moins de vibrations.

De la même façon, dans un système électrique triphasé, les trois phases sont identiques, mais elles fournissent leur puissance à des moments différents. Par conséquent, le flux total de puissance est très uniforme.

De plus, comme les phases sont identiques, on peut en considérer une seule comme étant représentative des trois. Retenons, sans pousser plus loin l'analogie, qu'un système triphasé est composé essentiellement de trois systèmes monophasés fonctionnant en séquence.

Afin de faciliter l'analyse des circuits triphasés, nous étudierons tout d'abord les circuits diphasés, bien que ces derniers ne soient plus utilisés que dans des applications spéciales.

Alternateur diphasé

Au cours de l'étude de l'alternateur monophasé (section Tension induite dans un conducteur), nous avons vu qu'une tension alternative apparaît aux bornes d'un enroulement lorsqu'il est coupé par le flux magnétique d'un aimant tournant.

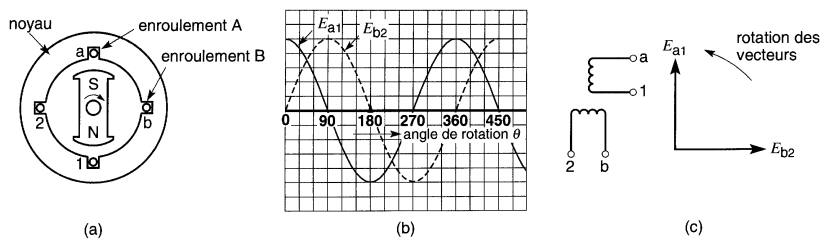
Considérons maintenant deux enroulements identiques montés sur un noyau d'acier et disposés en quadrature, c'est-à-dire décalés de 90° l'un par rapport à l'autre, (Fig. 26-1a).

Figure 26-1

a. Alternateur diphasé

b. Tensions alternatives générées par les enroulements A et B de l'alternateur;

c. Diagramme vectoriel des tensions

Leurs bornes sont respectivement identifiées par les symboles a,1 et b,2. Quand on fait tourner le rotor, des tensions E_a1 et E_b2 sont induites dans chacun des enroulements. Ces tensions ont évidemment même valeur et même fréquence; cependant, elles n'atteignent pas leur valeur maximale en même temps.

En effet, à l'instant où l'aimant occupe la position indiquée à la Fig. 26-la, la tension E_a1 passe par sa valeur maximale positive, tandis que la tension E_b2 est nulle.

Dès que le rotor a complété un quart de tour (ou 90°), la tension E_a1 devient nulle à son tour, tandis que la tension E_b2 atteint sa valeur maximale positive. Ces deux tensions sont donc déphasées de 90°. Elles sont représentées sous forme de courbes à la Fig. 26-1b, et vectoriellement à la Fig. 26-1c.

Chacune des tensions E_a1 et E_b2 est une tension monophasée possédant les mêmes propriétés que la tension alternative simple que nous avons déjà étudiée.

Sur la Fig. 26-2a, elles alimentent chacune un circuit distinct; le circuit raccordé aux bornes a,1 et celui raccordé aux bornes b,2 sont identifiés comme étant respectivement la phase A et la phase B. L'ensemble constitue un système à deux phases et l'alternateur est dit diphasé.

Figure 26-2 a. Alternateur diphasé en charge; b. Diagramme vectoriel des tensions et des courants

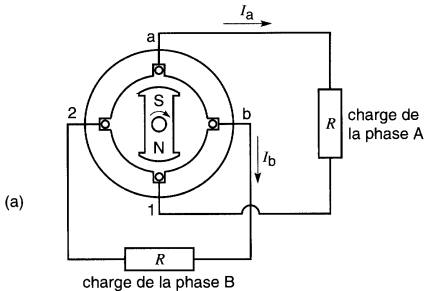
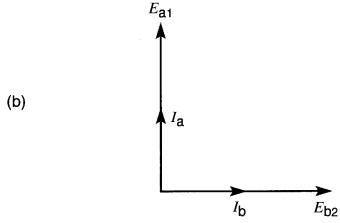
Si une charge résistive est branchée sur chacune des phases, les courants la et lb sont respectivement en phase avec les tensions E_a1 et E_b2  (Fig. 26-2b). Ces deux courants sont donc également déphasés de 90° dans le temps, c'est-à-dire que I_a atteint sa valeur maximale positive un quart de période avant I_b.

Alternateur triphasé

Un alternateur triphasé est semblable à un alternateur diphasé, sauf que le stator porte trois enroulements identiques au lieu de deux. Les trois enroulements sont disposés à 120° l'un de l'autre, comme l'indique la Fig. 26-3a.

Figure 26-3
a. Alternateur triphasé;
b. Tensions alternatives générées par les trois enroulements ;
c. Diagramme vectoriel des tensions induites

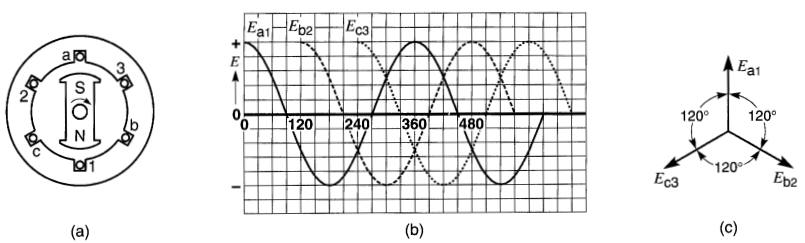
Lorsque le rotor tourne à vitesse constante, les tensions induites dans les trois enroulements ont même valeur efficace, mais elles n'atteignent pas leur valeur maximale en même temps.

En effet, à l'instant où l'aimant occupe la position indiquée sur la Fig. 26-3a, seule la tension E_a1 passe par sa valeur maximale positive.

La deuxième tension E_b2 atteint sa valeur maximale positive quand le rotor a tourné d'un angle de 120° (soit un tiers de tour). Enfin, la tension E_c3 atteint sa valeur maximale positive lorsque le rotor a tourné d'un angle de 240° (ou 2/3 de tour) par rapport à la position initiale.

Les trois tensions E_a1, E_b2 et E_c3, déphasées l'une de l'autre de 120°, sont représentées sous forme de courbes sinusoïdales à la Fig. 26-3b, et vectoriellement à la Fig. 26-3c.

Montage en étoile

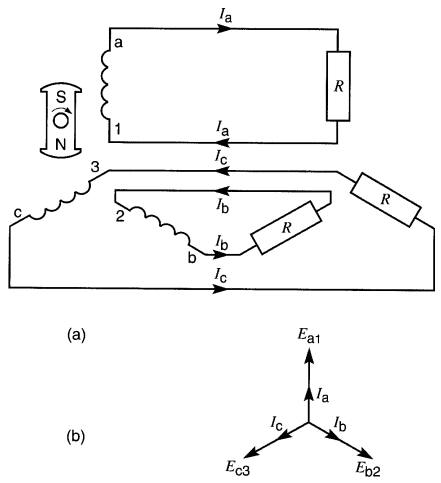
Les trois enroulements d'un alternateur triphasé pourraient alimenter trois circuits distincts (Fig. 26-4a). Cet arrangement exigerait 6 fils pour alimenter la charge totale constituée par trois charges monophasées. Si chaque phase alimente une charge résistive, les courants I_a, I_b et I_c le sont respectivement en phase avec les tensions E_a1, E_b2 et E_c3.

Si, de plus, les trois résistances sont égales, les courants ont la même valeur efficace, mais ils sont déphasés de 120° l'un de l'autre (Fig. 26-4b).

Figure 26-4
a. Système à 3 phases, 6 fils;
b. Diagramme vectoriel des tensions et des courants

On peut toutefois réduire le nombre de fils de ligne en groupant les trois fils de retour en un seul (Fig. 26-5).

Figure 26-5
a. Système à 3 phases, 4 fils;
b. Le courant dans le fil neutre est nul

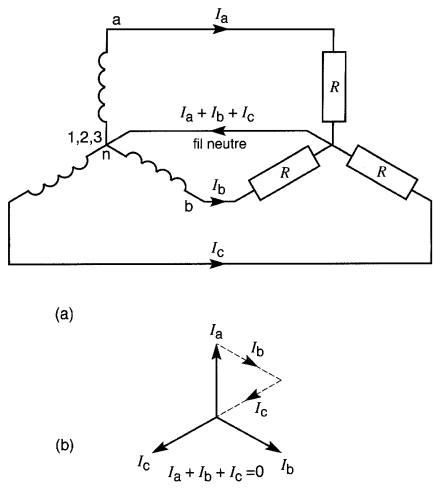
Ce fil de retour, appelé fil neutre (ou phase neutre), porte la somme des trois courants de sorte que

I_neutre = (I_a + I_b + I_c)

À première vue, il semble que la section du fil neutre doive être trois fois plus grande que celle des lignes a, b et c. Cependant, le diagramme vectoriel de la Fig. 26-5b montre que la somme vectorielle de ces trois courants est nulle.

Par conséquent, I_neutre = 0

On peut donc enlever le fil neutre complètement sans que les tensions ou les courants soient affectés (Fig. 26-6).

Fig. 26-6 Système à 3 phase, 3 fils

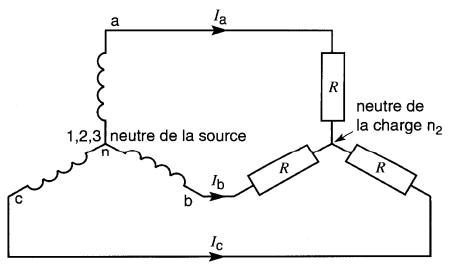
On réalise du même coup une forte économie sur la ligne de transport. Toutefois, il faut remarquer que, pour supprimer le fil neutre, les trois charges doivent être identiques.

Si les charges ne sont pas identiques, l'absence de fil neutre occasionne un déséquilibre des tensions sur les trois charges. Le circuit de l'alternateur et de la charge de la Fig. 26-6 est appelé montage en étoile à trois fils, tandis que celui de la Fig. 26-5 est un montage en étoile à quatre fils.

La plupart des alternateurs triphasés sont montés en étoile, avec 3 ou 4 fils de sortie. Les lignes qui sortent de l'alternateur sont généralement appelées phases*, tout comme les trois enroulements eux-mêmes.

Le terme «phase» peut avoir différentes significations selon le contexte.

Les exemples suivants montrent comment le terme est utilisé:

1. le courant est en phase avec la tension (dans un diagramme vectoriel);

2. les trois phases d'une ligne de transport (désigne les trois conducteurs de la ligne);

3. la tension entre les phases (signifie la tension entre les lignes);

4. la séquence des phases (désigne l'ordre dans lequel les vecteurs de tension se suivent dans un montage triphasé) ;

5. la phase grillée d'un moteur (désigne l'enroulement grillé d'un moteur triphasé) ;

6. les courants de phase sont équilibrés (signifie que les courants dans un montage triphasé sont égaux et décalés de 120°);

7. les phases sont déséquilibrées (signifie que les tensions d'une ligne triphasée ne sont pas égales et qu'elles ne sont pas décalées de 120°).

Propriétés du montage en étoile

La Fig. 26-7a représente, de façon schématique, la disposition des trois enroulements sur l'induit d'un alternateur.

Figure 26-7
a. Enroulements d'un alternateur raccordés en étoile;
b. Diagramme vectoriel des tensions ligne à neutre ;
c. Construction du vecteur de tension E_ab ;
d. Les tensions E_ab, E_bc, E_ca sont égales et déphasées de 120°

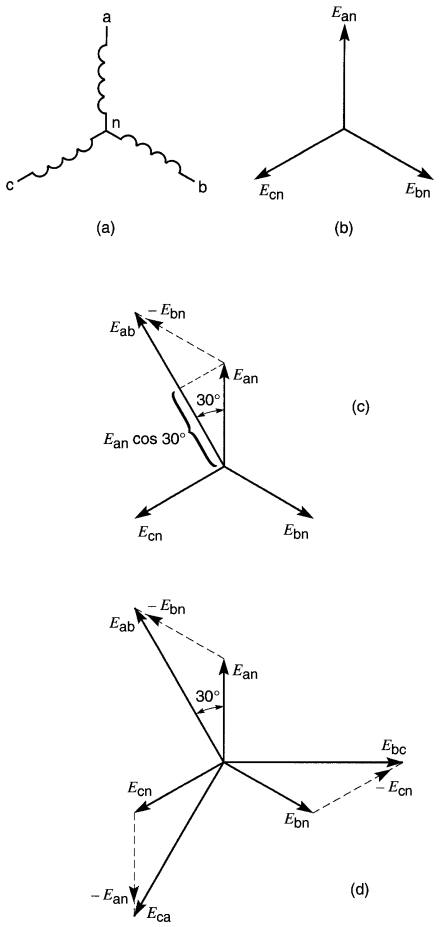
Les bornes 1, 2, 3 sont raccordées ensemble pour former une seule borne n, appelée neutre. Le diagramme vectoriel des trois tensions induites E_an, E_bn, E_cn est montré à la Fig. 26-7b.

Supposons que leur valeur efficace soit de E_LN volts. Quelle est alors la valeur des tensions entre les bornes a, b et c?

 D'après la première loi de Kirchhoff, et en suivant d'abord la boucle a, b, n dans le sens horaire, on peut écrire l'équation suivante:

E_ab + E_bn + E_na =0

donc E_ab = -E_na - E_bn

soit E_ab = E_an - E_bn

Cette somme vectorielle donne le vecteur E_ab montré à la Fig. 26-7c. Il est 30° en avance sur le vecteur E_an et sa valeur efficace E_L est donnée par:

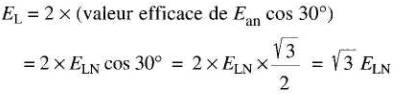
En choisissant, à tour de rôle, les boucles b, c n, et c, a, n, on obtient exactement la même valeur efficace pour la tension entre les bornes b, c et c, a.

En effet,

E_bc = E_bn- E_cn et E_ca = E_cn- E_an

Le diagramme vectoriel complet est montré à la Fig. 26-7d. On constate que les tensions E_ab, E_bc et E_ca entre les lignes sont aussi déphasées entre elles de 120°.

Pour une ligne triphasée on peut donc écrire :

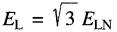    (26-1)

oò

E_L = tension entre les lignes [V]

E_LN = tension entre les lignes et le neutre [V]

√3= constante [valeur approximative = 1,73]

Afin de clarifier davantage ces résultats, nous montrons à la Fig. 26-8 un alternateur dont la tension ligne à neutre est de 100V. Les tensions entre les lignes sont toutes égales et leur valeur est 100 x √3 volts ou 173V.

Figure 26-8 Tensions produites par un alternateur connecté en étoile

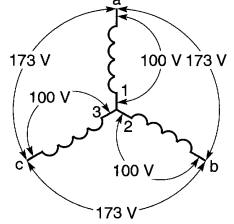
Pour le montage en étoile, les tensions de ligne à ligne sont donc 1,73 fois plus grandes que les tensions de ligne à neutre.

Les termes ligne-ligne et ligne-neutre sont aussi utilisés. Lorsqu'on donne la tension d'un système triphasé ou d'une machine triphasée sans spécifier s'il s'agit d'une tension ligne-neutre ou ligne-ligne, il est entendu qu'il s'agit de la tension efficace ligne à ligne. Par exemple, si l'on parle d'une ligne de distribution de 24,9 kV, il est entendu que cette tension désigne la tension efficace ligne à ligne ou phase-phase.

Les tensions entre les lignes a, b, e constituent un système triphasé, mais la tension entre deux lignes quel conques (a et b, b et c, ou c et a) demeure une tension monophasée.

Exemple 26-1

Un alternateur triphasé à 60 Hz génère une tension sinusoïdale de 23 900V entre les lignes.

Calculer:

a) la tension efficace entre une ligne et le neutre

b) la tension crête entre deux lignes

c) l'intervalle de temps qui sépare les valeurs crête positives des tensions E_ab et E_bc

Solution

a) La tension ligne à neutre E_LN est:

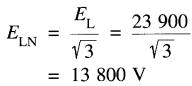
b) La tension crête entre deux lignes est:

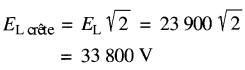
c) Un angle de 120° sépare les vecteurs E_ab et E_bc. Comme un cycle (360°) a une durée de 1/60 s, l'intervalle entre les valeurs crêtes positives de E_ab et de E_bc est:

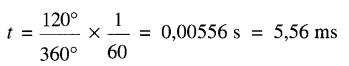
Charges raccordées en étoile et en triangle

Pour que les courants dans les trois lignes d'un système triphasé soient égaux, il faut que la charge soit équilibrée, condition rencontrée très souvent dans les circuits triphasés.

Une charge triphasée est dite équilibrée lorsqu'elle est constituée de trois impédances identiques. Les trois impédances peuvent être montées en étoile (Fig. 26-9a) ou en triangle (Fig. 26-9b).

Figure 26-9a Charge triphasée équilibrée montée en étoile

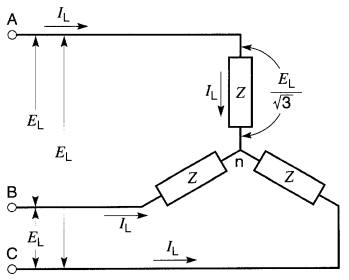
Figure 26-9b Charge triphasée équilibrée montée en triangle

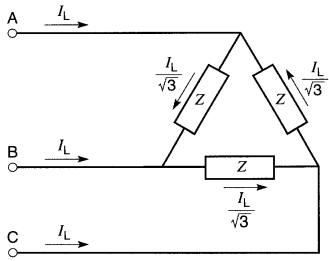
Les relations entre les tensions et les courants de chaque élément, par rapport à la tension de ligne E_L et au courant de ligne I_L, sont indiquées sur ces figures.

Pour le montage en étoile, il est facile de comprendre d'après ce que nous venons d'expliquer, que les règles suivantes s'appliquent:

CONNEXION EN ÉTOILE

1. le courant dans chaque élément est égal au courant I_L dans la ligne

2. la tension aux bornes de chaque élément est égale à la tension E_L de ligne à ligne divisé par 3

3. les trois tensions aux bornes des éléments sont déphasées de 120°

4. les trois courants dans les éléments sont déphasés de 120°

En ce qui concerne le raccordement en triangle, déterminons les relations entre les tensions et les courants en supposant une charge résistive (Fig. 26-10a).

Figure 26-10

a. Charge triphasée équilibrée montée en triangle ;

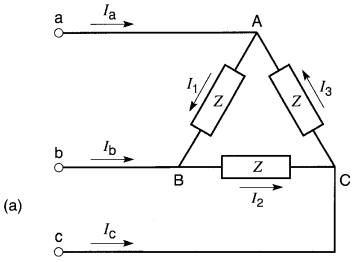
b. Diagramme vectoriel pour une charge résistive

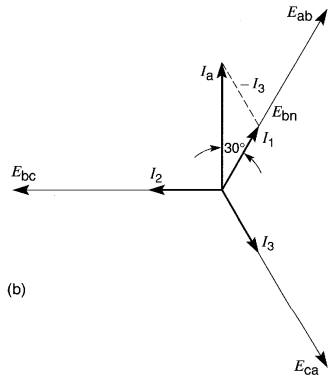
Les résistances étant branchées entre les lignes, les courants I₁, I₂, I₃ sont en phase avec les tensions correspondantes Eab, E_bc et E_ca (Fig. 26-10b). Ces dernières sont créées par un alternateur qui n'apparaît pas sur la figure.

Si on examine le nceud A de la ligne a, la deuxième loi de Kirchhoff nous permet d'écrire :

I_a = I₁ - I₃

En faisant cette somme vectorielle, on constate que le vecteur I_a se trouve 30° en avance sur le vecteur I₁.

De plus, les relations géométriques de la Fig. 26-10b indiquent que la valeur efficace de I_a est √3 fois plus grande que la valeur efficace de I₁ (ou de I₃). À cause de la symétrie du montage pour les trois phases, on peut écrire:

I_L = I√3 (26-2)

où

I_L  = courant dans les lignes [A]

I = courant dans chaque branche de la connexion en triangle [A]

√3 = constante [valeur approximative = 1,73]

Nous concluons que pour un montage en triangle (Fig. 26-9b), les règles suivantes s'appliquent :

CONNEXION EN TRIANGLE

1. le courant dans chaque élément est égal au courant I_L dans la ligne divisé par 3

2. la tension aux bornes de chaque élément est égale à la tension E_L de ligne à ligne

3. les tensions aux bornes des éléments sont déphasées de 120°

4. les courants dans les éléments sont déphasés de 120°

Exemple 26-2

Une ligne triphasée à 550V (ligne à ligne) alimente trois résistances identiques montées en étoile.

Quelle est la tension aux bornes de chaque résistance?

Solution

La tension aux bornes de chaque résistance est égale à la tension de ligne à neutre soit :

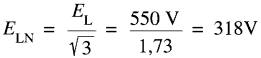
Exemple 26-3

Trois impédances identiques montées en triangle sur une ligne triphasée à 550V tirent un courant de ligne de 10A.

Calculer:

a) le courant dans chaque impédance et la tension à ses bornes

b) la valeur des impédances

Solution

a) Le courant dans chacune des impédances est:

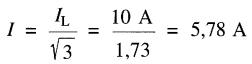
et la tension aux bornes de chacune est EL = 550V.

b) la valeur de chaque impédance est :

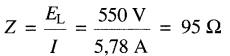
Puissance transportée par une ligne triphasée

On a souvent à calculer la puissance transportée par une ligne triphasée en fonction de sa tension E_L et du courant de ligne I_L. Calculons tout d'abord la puissance active absorbée par une charge constituée de trois résistances identiques montées

a) en étoile et b) en triangle.

Pour le montage en étoile (Fig. 26-9a):

le courant dans chaque résistance est I_L ampères;

la tension aux bornes de chaque résistance est de E_L√3 volts;

la puissance active P_z absorbée par chaque résistance est donc:

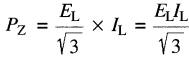
la puissance totale absorbée par les trois résistances est trois fois plus grande, soit :

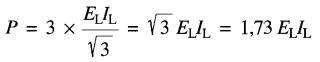
Pour le montage en triangle (Fig. 26-9b):

le courant dans chaque résistance est :

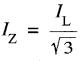
la tension aux bornes est E_L volts;

la puissance active P_z absorbée par chaque résistance est donc :

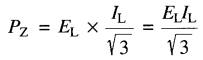
la puissance totale absorbée par les trois résistances est trois fois plus grande, soit:

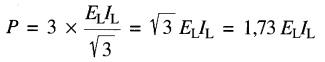
On arrive au même résultat, que le montage soit raccordé en étoile ou en triangle. Or, la puissance dissipée dans les résistances est évidemment égale à celle fournie par la ligne; il en résulte que la puissance active transportée par la ligne vaut:

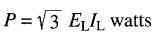
D'une façon générale, et pour une charge équilibrée, la puissance apparente totale transportée par une ligne triphasée est donnée par la formule:

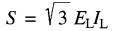    (26-3)

où

S = puissance apparente totale transportée par la ligne triphasée, en volts-ampères [VA]

E_L = tension de ligne à ligne (et non de ligne à neutre), en volts [V]

I_L = courant de ligne, en ampères [A]

Les relations entre les puissances active P, réactive Q, et apparente S sont les mêmes dans les circuits triphasés équilibrés que dans les circuits monophasés. Il en est de même pour le facteur de puissance d'un circuit triphasé.

On a donc :

S² = P² + Q² (26-4)

et

FP = P / S (26-5)

où

P = puissance active du circuit triphasé [W]
S = puissance apparente du circuit triphasé [VA]
Q = puissance réactive du circuit triphasé [var]

Exemple 26-4

Un moteur triphasé raccordé à une li ne à 480V tire un courant de 5A dans chaque fil.

a) Calculer la puissance apparente fournie au moteur

b) Quelle est la puissance active fournie au moteur sachant que son facteur (le puissance est de 80%?

 Solution

a) la puissance apparente totale est:

S = √3E_LI_L = 1,73 x ,480 x 5 = 4157 VA = 4,16 kVA

b) la puissance active totale est:

P= S x FP = 4,15 x 0,80 = 3,32 kW

Résolution des circuits triphasés

On peut résoudre assez facilement les circuits triphasés équilibrés en ne considérant qu'une seule phase. En effet, une charge triphasée équilibrée est tout simplement un ensemble de trois charges identiques monophasées.

Les exemples qui suivent illustrent comment on doit procéder.

Exemple 26-5

Trois résistances égales montées en étoile sur une ligne triphasée à 600V dissipent une puissance totale de 3000 W (Fig. 26-11).

Figure 26-11 Voir exemple 26-5

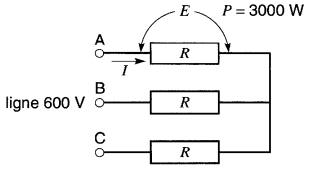
Calculer:

a) le courant dans chaque ligne

b) la valeur de chaque résistance

Solution

a) Puissance dissipée par chaque résistance :

P = 3000 W / 3 = 1000 W

Tension aux bornes de chaque résistance :

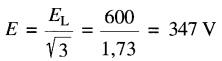
Courant dans chaque résistance :

I = P / E = 100W / 347V = 2,88A

Le courant dans chaque ligne est également de 2,88 A.

On obtient directement ce résultat en appliquant la formule 26-3, soit:

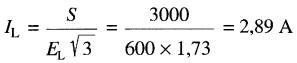
b) Résistance de chaque élément:

R = E / I = 347V / 2,89A = 120Ω

Exemple 26-6

Dans le circuit de la Fig. 26-12.

Figure 26-12 Voir exemple 26-6

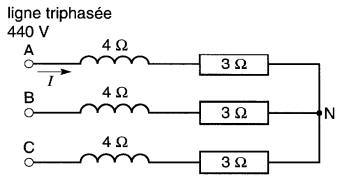
calculer: a) le courant dans chaque ligne b) la tension aux bornes des inductances

Solution

a) Chacune des trois branches du circuit comprend une réactance inductive X_L = 4Ω et une résistance R = 3Ω. Chaque branche est soumise à la tension monophasée qui existe entre une ligne et le neutre.

Cette tension a pour valeur:

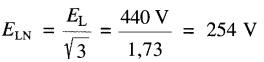
L'impédance de chaque phase est:

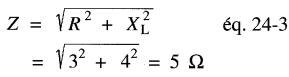
Le courant dans chaque élément est donc :

I = 254 V / 5Ω = 50,8 A

Ce courant est aussi le courant de ligne.

b) La tension aux bornes de chaque inductance est :

E = IX_L =50,8A x 4Ω = 203V

Exemple 26-7

Une ligne triphasée à 550V, 60 Hz, alimente trois condensateurs identiques montés en triangle (Fig. 26-13).

Figure 26-13 Voir exemple 26-7

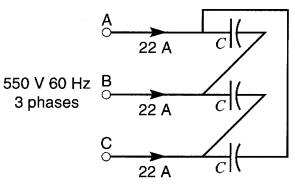
Le courant de ligne est de 22A. Calculer la capacitance de chaque condensateur.

Solution

Courant dans chaque condensateur:

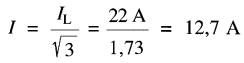
Tension aux bornes de chaque condensateur:

E_L = 550V

Réactance capacitive X_c de chaque condensateur :

X_c = 550V / 12.7A = 43,3Ω

d'où la capacitance C:

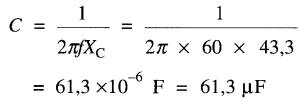
Charges industrielles

Il arrive souvent que l'on ne sache pas si une charge triphasée est raccordée en étoile ou en triangle. Par exemple, les moteurs, condensateurs, etc., ne présentent que 3 bornes de raccordement, de sorte qu'il est impossible de dire comment les connexions sont effectuées à l'intérieur.

Dans ces circonstances, comme il est plus facile de traiter une connexion en étoile qu'une connexion en triangle, on suppose que le raccordement est en étoile. L'hypothèse d'une connexion en étoile peut être appliquée non seulement à des charges individuelles, mais aussi à des usines entières ou des centres commerciaux qui comprennent des milliers de charges dont on ignore la connexion.

En voici deux exemples.

Exemple 26-8

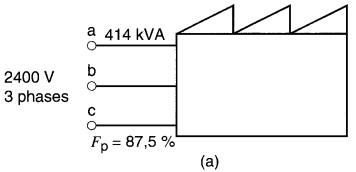
Une usine absorbe 414 kVA d'une ligne triphasée à 2400 V (Fig. 26-14a).

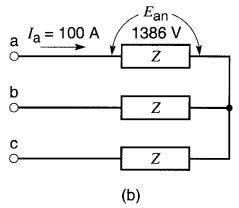
Figure 26-14

a. Tension et puissance à l'entrée d'une usine (voir exemple 26-8) ;

b. Circuit équivalent de l'usine ;

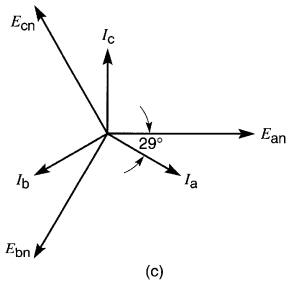
c. Diagramme vectoriel des tensions et des courants

La charge est assez bien équilibrée, et le facteur de puissance est de 87,5% (en retard).

Déterminer:

a) l'impédance de l'usine, par phase

b) l'angle entre le courant de lime et la tension ligne à neutre

c) le diagramme vectoriel complet de l'usine

Solution

a) Nous modélisons la charge de l'usine en la représentant par trois impédances raccordées en étoile (Fig. 26-14b).

La tension par phase est:

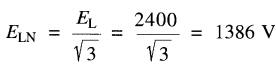
La puissance apparente par phase est:

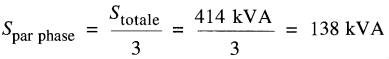
Le courant par phase est:

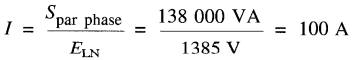
d'où l'impédance par phase:

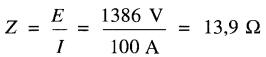
b) L'angle entre le courant et la tension ligne à neutre est donné par:

θ = arccos (FP) = arccos 0,875 = 29° éq. 25-7

Le courant est en retard sur E_LN de 29°, dans chaque phase.

c) Le diagramme vectoriel est montré à la Fig. 26-14c. En pratique, on simplifierait le diagramme en ne montrant qu'une seule phase, soient les vecteurs E_an, I_a, et l'angle entre les deux.

Exemple 26-9

Un moteur de 5000 hp tire un courant de 462A d'une ligne triphasée à 4000V (Fig. 26-15).

Figure 26-15 Charge composée d'un gros moteur et d'un banc de condensateurs pour améliorer le facteur de puissance de la ligne (voir exemple 26-9)

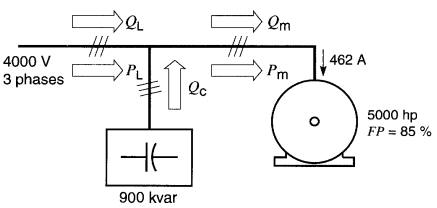
Le facteur de puissance du moteur est de 85%. Un banc de condensateurs de 900 kvar est installé aux bornes du moteur pour améliorer le facteur de puissance de la liegne.

Calculer:

a) la puissance active absorbée par le moteur
b) la puissance réactive absorbée par le moteur
c) la puissance réactive fournie par la ligne
d) le courant tiré de la ligne
e) Tracer le diagramme vectoriel pour une phase

Solution

Dans cet exemple, nous appliquerons une autre approche, en utilisant les puissances actives, réactives et apparentes totales, au lieu de leur valeur par phase.

a) La puissance apparente absorbée par le moteur est:

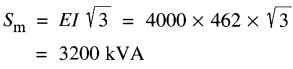
La puissance active absorbée par le moteur est:

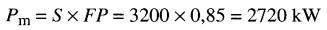
b) La puissance réactive absorbée par le moteur est :

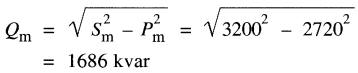
c) La puissance réactive fournie par la ligne est la différence entre Q_m et la puissance réactive Q_c fournie par le banc de condensateurs.

Q_L = Q_m - Q_c = 1686 - 900 = 786 kvar

d) La puissance active fournie par la ligne est la même que celle absorbée par le moteur, soit:

P_L = 2720 kW

La puissance apparente fournie par la ligne est:

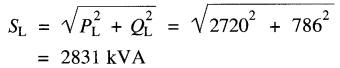
Le courant tiré de la ligne est:

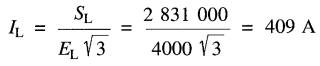
e) Le facteur de puissance de la ligne est:

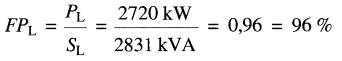
L'angle entre le courant de 409A et la tension ligne à neutre est:

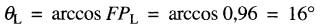
La tension ligne à neutre est :

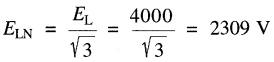
Courant triphasé tiré par le banc de condensateurs :

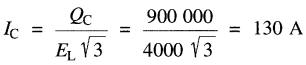
Ce courant est 90° en avance sur la tension E_LN.

L'angle entre le courant de 462A tiré par le moteur et la tension E_LN est:

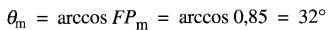
Ces informations nous permettent de tracer le diagramme vectoriel pour une phase (Fig. 26-16a). On prend E_LN comme vecteur de référence parce qu'il est commun à tous les équipements.

Séquence des phases

En plus de sa tension et de sa fréquence, un système triphasé possède une propriété importante appelée séquence des phases.

Dans une ligne triphasée, la séquence des phases est l'ordre dans lequel les trois tensions maximales positives se succèdent.

Comme on le verra à la section Alternateurs triphasés, le sens de rotation des moteurs triphasés dépend de la séquence des phases, et la mise en parallèle des lignes triphasées ne peut se faire que si les séquences sont les mêmes.

Pour ces raisons, il est souvent nécessaire de connaître la séquence des phases en plus de la valeur et de la fréquence des tensions. On peut facilement comprendre le concept de séquence des phases en considérant l'analogie suivante.

Supposons que les lettres a, b, c soient inscrites à intervalles de 120° sur un disque tournant autour d'un axe (Fig. 26-17).

Figure 26-17 Les lettres apparaissent dans la séquence a-b-c

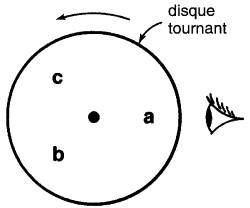
Si le disque tourne dans le sens antihoraire, les lettres se présenteront à un observateur dans la séquence a-b-c-a-b-c-, etc. Cette séquence est appelée séquence directe ou séquence a-b-c.

Dans les manuels anglais, les séquences directe et inverse sont respectivement désignée par positive sequence et negative sequence.

Par contre, si le disque tournait dans le sens horaire, l'observateur verrait la séquence a-c-b-a-c-b-, etc. (Fig. 26-18). Cette séquence s'appelle séquence inverse ou séquence a-c-b.

Figure 26-18 Les lettres apparaissent dans la séquence a-c-b

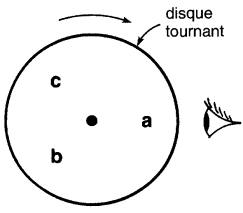
 Intervertissons maintenant deux lettres quelconques sur le disque de la Fig. 26-17, tout en gardant le sens de rotation antihoraire.

Par exemple, si on intervertit les lettres a et c, on obtient le résultat montré à la Fig . 26- 19.

Figure 26-19 Les lettres apparaissent dans la séquence a-c-b

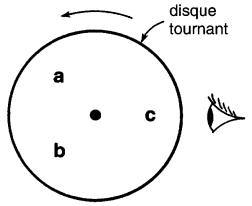
Pour l'observateur, la séquence est c-b-a-c-b-a-, etc., soit en abrégé a-c-b. C'est donc la même séquence que celle générée par le disque de la Fig . 26-18. Nous concluons qu'on peut convertir une séquence directe en séquence inverse en intervertissant deux des trois lettres. Considérons maintenant une source triphasée possédant les bornes a, b, c (Fig. 26-20).

Figure 26-20 La tension triphasée entre les lignes a, b, c est fidèlement représentée par le diagramme vectoriel . La séquence est a-b-c (séquence directe)

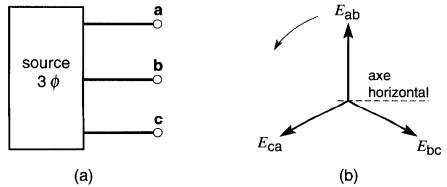
Supposons que les tensions entre les bornes soient fidèlement représentées par les vecteurs tournants

Eab, Ebc, Eca

Comme ces derniers tournent dans le sens antihoraire, ils traversent l'axe vertical dans la séquence :

Eab Ebc Eca Eab Ebc Eca

En ne retenant que les indices de cette série de tensions, on obtient la séquence ab-be-ca-ab-be-ca-, ce qu'on peut écrire sous la forme abbccaabbccaa. . ., etc.

En remplaçant les lettres doubles par une seule, on obtient la séquence a-b-c. Par définition, on dit que la séquence des phases est a-b-c, ou que les tensions générées par la source sont en séquence directe.

Exemple 26-10

La séquence des phases dans la Fig . 26-21 est A-C- B (séquence inverse).

Figure 26-21 Voir exemple 26-10

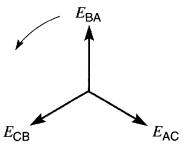
Tracer le diagramme vectoriel des tensions de ligne.

Solution

Les tensions suivent la séquence A - C - B, ce qui est équivalent à la séquence AC - CB - BA- AC.

Par conséquent, la séquence des tensions est EAC- EcB- EBA

Le diagramme vectoriel correspondant est donné à la Fig. 26-21 . Noter que l'orientation de l'ensemble des trois vecteurs n'a pas d'importance, c'est leur position relative qui indique la séquence. En ce qui concerne la charge, on peut inverser la séquence des phases d'une ligne triphasée en intervertissant simplement deux conducteurs.

Bien que cette opération semble triviale, elle peut créer un problème majeur lorsqu'il s'agit d'intervertir les grosses barres omnibus alimentant un moteur triphasé. Il en serait de même s'il fallait intervertir les conducteurs d'une ligne de transport à 500 kV.

En pratique, afin d'éviter ces problèmes, on tient compte de la séquence des phases lors de la planification du réseau. La séquence des phases de tous les réseaux de transport, de répartition et de distribution est connue d'avance, et toute modification à ces réseaux en tient compte.

Détermination de la séquence des phases

Bien qu'il existe des instruments spéciaux pour dé- terminer la séquence des phases, on peut en fabriquer un très simplement en branchant en étoile deux lampes à incandescence identiques et un condensateur (Fig . 26-22a).

Figure 26-22 a. Montage simple pour déterminer la séquence des phases ; b. Diagramme vectoriel des tensions

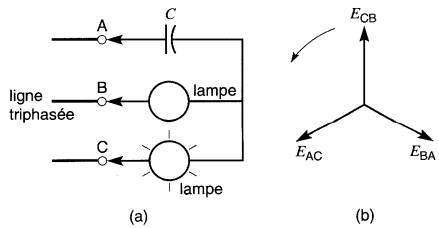
Si l'on branche ce montage aux trois fils de lignes, sans raccorder le neutre, une lampe brillera toujours plus que l'autre* et la séquence des phases sera dans l'ordre: lampe brillante - lampe faible - condensateur.

Afin d'observer une différence notable dans l'éclairage, il faut que l'impédance du condensateur soit comprise entre un dixième et dix fois la résistance nominale d'une lampe.

Dans la Fig. 26-22a, la séquence est donc C-B-A (ou A-C-B). Le diagramme vectoriel correspondant est donné à la Fig. 26-22b.

Mesure de la puissance active (circuits triphasés à 3 fils)

La puissance active fournie à une charge triphasée à trois fils peut être mesurée au moyen de deux watt-mètres montés suivant le schéma de la Fig . 26-23.

Figure 26-23 Méthode de raccordement de deux wattmètres dans un circuit à 3 phases, 3 fils

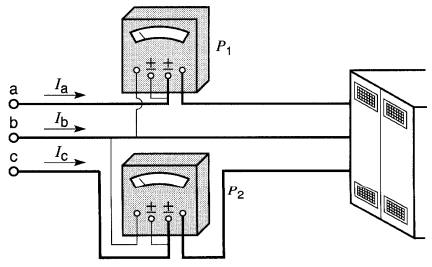
La puissance totale fournie à la charge est égale à la somme des puissances indiquées par les deux watt- mètres. Si le facteur de puissance de la charge est inférieur à 100 %, les valeurs indiquées par chacun des instruments sont différentes .

De plus, si le FP de la charge est inférieur à 50 %, l'aiguille de l'un des deux wattmètres tend même à dévier dans le mauvais sens, c'est-à-dire qu'il donne une lecture négative. Il faut alors inverser les connexions de la bobine de courant ou de la bobine de potentiel de ce wattmètre afin d'obtenir une indication numérique de cette quantité négative.

Dans ce cas, c'est la différence entre les valeurs indiquées par les wattmètres qui donne la puissance du circuit triphasé.

La méthode des deux wattmètres donne la puissance active totale, même si les charges sont déséquilibrées. De plus, la mesure ne dépend pas de la séquence des phases. La Fig. 26-24 montre un wattmètre triphasé utilisé pour mesurer la puissance totale sur un réseau.

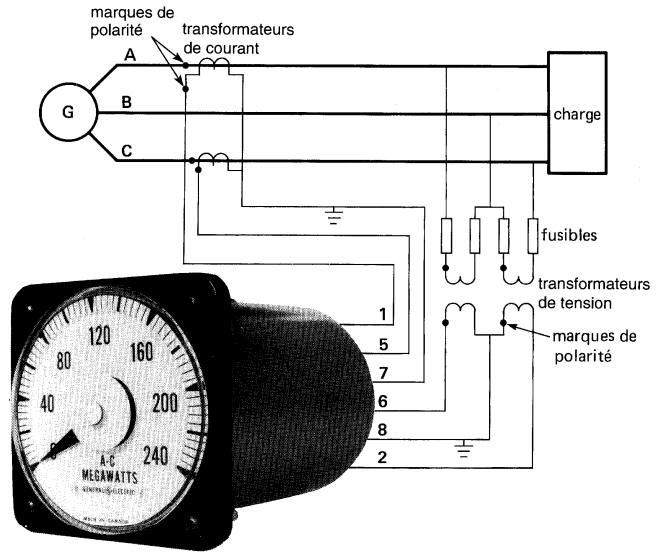
Figure 26-24

Wattmètre utilisé pour la mesure de la puissance active dans une ligne triphasée à 3 fils. Les transformateurs de potentiel et de courant sont intercalés entre la ligne triphasée et l'instrument, selon le schéma de raccordement montré ci-dessus. Le wattmètre lui-même est doté d'un multiplicateur Et qui génère une tension à courant continu proportionnelle à la puissance active totale.

L'aiguille est donc actionnée par un simple mouvement d'Arsonval (voir aussi la figure 25-10 section Puissance active, réactive et apparente montrant un varmètre triphasé fonctionnant selon le même principe) (gracieuseté de Cie Générale Électrique)

Exemple 26-11

Un essai a deux wattmètres sur un moteur triphasé donne les résultats suivants :

P₁ +5950 W     P₂= +2355 W

Les courants dans les trois fils de ligne sont de 10 A et la tension entre les lignes est de 600V.

Calculer le FP du moteur.

Solution

Puissance apparente fournie au moteur:

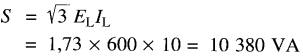
Puissance active fournie au moteur :

P = 5950 + 2355 = 8305 W

d'où le facteur de puissance:

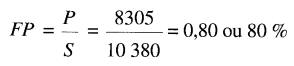
Mesure de la puissance active (circuits triphasés à 4 fils)

Pour mesurer la puissance dans les circuits triphasés à quatre fils, on doit utiliser trois wattmètres. La bobine de courant de chacun des wattmètres est en série avec un fil de phase. La bobine de potentiel est connectée entre le fil neutre et le fil de phase correspondant (Fig . 26-25).

Figure 26-25 Méthode de raccordement de trois wattmètres dans un circuit à 3 phases, 4 fils

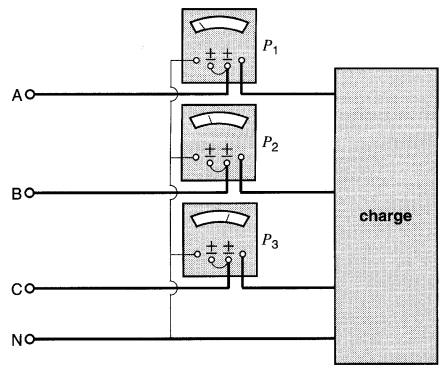
La puissance totale fournie à la charge est égale à la somme des puissances indiquées par les trois wattmètres. La méthode des trois wattmètres donne la puissance active totale, même si les charges sont déséquilibrées .

Mesure de la puissance réactive

Le varmètre indique la puissance réactive dans un circuit. Sa construction est identique à celle d'un watt- mètre, mais la tension appliquée sur la bobine de potentiel est décalée de 90° par rapport à son angle réel. On rencontre les varmètres surtout dans les salles de commande des centrales, les postes et les grandes usines.

Dans les montages expérimentaux triphasés (3 fils ou 4 fils), on peut mesurer la puissance réactive en utilisant deux wattmètres branchés selon le schéma de la Fig. 26-23. Il suffit de multiplier la différence des lectures par le facteur √3.

Remarquer que cette méthode s'applique seulement aux circuits triphasés équilibrés.

Exemple 26-12

Dans l'exemple 26-11 montrant l'application de la méthode des deux wattmètres dans un circuit à 3 fils, les tensions de lignes sont équilibrées.

a) Calculer la puissance réactive tirée par le moteur

b) Connaissant P et Q, vérifier que le facteur de puissance est bien 80 %

Solution

a) Les wattmètres indiquent les valeurs respectives de +5950 W et +2355 W La puissance réactive tirée par le moteur est donc:

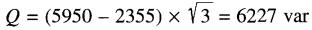
b) La puissance active P = 5950 + 2355 = 8305 W La puissance apparente:

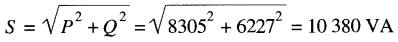
d'où le facteur de puissance:

FP = PIS = 8305/10380 = 0,80

La Fig. 25-10 montre un varmètre triphasé utilisé pour mesurer la puissance réactive totale dans une ligne.

Puissance instantanée d'un circuit triphasé

Lors de l'étude des circuits monophasés (section Circuits simples à courant alternatif, Fig. 22-3), nous avons vu que la puissance instantanée fournie à une résistance varie périodiquement entre zéro et un maximum. Le même phénomène se produit dans un circuit résistif triphasé.

Cependant, comme les tensions et les courants sont déphasés de 120°, il s'ensuit que les puissances actives des trois phases sont aussi déphasées .

La Fig. 26-26 montre les tensions ligne à neutre d'une charge triphasée et les ondes correspondantes des puissances instantanées Pa, Pb, Pc.

Figure 26-26 Schéma montrant que la puissance active totale d'un circuit triphasé équilibré est constante

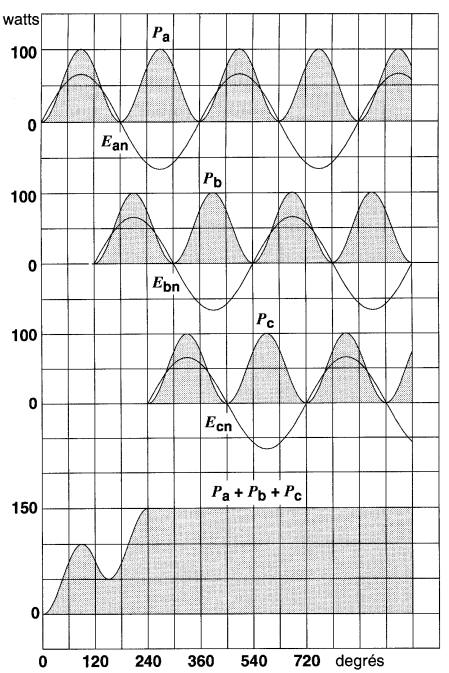
Si l'on additionne ces trois puissances, on constate que la puissance totale donne à tout instant une valeur constante. Cette puissance est égale à 1,5 fois la puissance crête d'une seule phase. Donc, dans un circuit triphasé équilibré, la puissance active instantanée totale est constante.

Nous verrons plus loin que cette propriété des puissances triphasées a un effet important sur le comportement des moteurs et des génératrices à courant alternatif.

Mesure de la puissance instantanée

Le wattmètre est un instrument qui multiplie la tension instantanée E par le courant instantané I et affiche la valeur moyenne de ce produit. Dans le wattmètre conventionnel, c'est par un moyen mécanique (inertie du cadre et de l'aiguille) que l'on obtient la valeur moyenne du produit E_L.

Dans les wattmètres électroniques, on utilise plutôt un multiplicateur qui donne la valeur instantanée du produit EL Ce multiplicateur peut être réalisé au moyen de composants électroniques ou d'un générateur à effet Hall. Ce dernier est composé d'un semi-conducteur spécial en forme de parallélépipède.

Le courant I passe par deux faces parallèles pendant qu'un flux Φp, proportionnel à la tension E, traverse deux autres faces (Fig. 26-27).

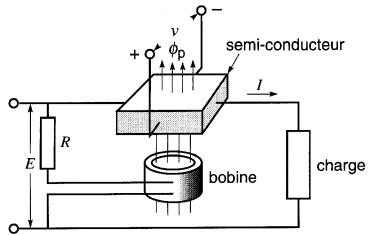
À cause de l'effet Hall, une tension v dont la valeur est proportionnelle au produit instantané I x Φp (donc au produit EI) apparaît alors entre les deux autres faces.

Si on applique cette tension aux bornes d'un oscillographe, on peut observer la forme d'onde de la puissance instantanée. La Fig. 26-26 montre trois de ces puissances instantanées . Elle peut aussi être appliquée sur un voltmètre à c.c. sensible dont l'aiguille fournira une indication proportionnelle à la puissance moyenne active, tout comme un wattmètre de construction conventionnelle.

Résumé

Les circuits triphasés sont utilisés pour la production, le transport et la distribution de l'énergie électrique, ainsi que pour l'alimentation des charges importantes. Nous avons vu qu'il existe deux façons de connecter les branches d'un circuit triphasé : le montage en étoile et le montage en triangle.

Il est important de retenir les relations entre les tensions ligne à ligne et les tensions ligne à neutre (montage en étoile), de même que les relations entre les courants de lignes et les courants de branches (montage en triangle). Retenons aussi la formule S = EI√3 donnant la puissance apparente S d'un circuit triphasé équilibré en fonction de la tension E et du courant I de ligne. Ces relations font toutes intervenir le facteur √3.

Nous avons vu que la résolution d'un circuit triphasé équilibré est simplifiée en ne considérant qu'une seule phase. Nous avons aussi appris comment déterminer la séquence des phases et comment mesurer les puissances active et réactive dans un circuit à trois ou quatre fils.

PROBLÈMES

Niveau pratique 26-1 Un alternateur triphasé connecté en étoile génère une tension de 2400V dans chacune de ses phases.

Quelle est la tension entre les 3 fils de sortie?

26-2 L'alternateur de la Fig. 26-3 génère une tension crête de 100V par phase.

Déterminer:

a) la valeur instantanée de la tension aux bornes al à 0°, 90°, 120°, 240° et 330°

b) la polarité de la borne a par rapport à la borne 1 à chacun des instants

c) la valeur instantanée de la tension aux bornes b2 aux mêmes instants

26-3 Dans le diagramme vectoriel de la Fig. 26-3c, la tension Eb2 est 120° en arrière de la tension Ea1. Peut-on dire également que la tension Eb2 est 240° en avant de la tension Ea1?

26-4 La tension entre les lignes a-b-cde la Fig. 26-6 est de 620 V.

a) Calculer la tension aux bornes de chaque résistance .

b) Si R = 15Ω, quel est le courant dans chaque ligne?

c) Quelle est la puissance fournie à la charge?

26-5 Trois charges résistives Z sont raccordées en triangle selon le schéma de la Fig. 26-10a. La tension entre les lignes A - B - C est de 13,2 kV et le courant dans les fils de ligne est de 1202 A.

Calculer:

a) le courant dans chaque résistance

b) la tension aux bornes de chaque résistance

c) la puissance fournie à chaque résistance

d) la puissance totale fournie à la charge

26-6

a) Quelle est la séquence des phases dans la Fig. 26-10: a-c-b ou a-b-c?

b) Comment peut-on inverser cette séquence?

26-7 Un moteur triphasé est alimenté par une ligne à 600V. Le courant tiré de la ligne étant de 25A, quelle est la puissance apparente fournie au moteur?

26-8 Trois lampes à incandescence de 60W, 120V sont raccordées en triangle. Quelle doit être la valeur de la tension d'alimentation triphasée pour que les lampes éclairent normalement?

26-9 Représenter par un schéma le montage d'un wattmètre dans un circuit monophasé .

26-10 Donner le montage de deux wattmètres dans un circuit triphasé à 3 fils.

Niveau intermédiaire

26-11 Trois résistances de 10Ω sont connectées en triangle sur une ligne triphasée à 208V.

a) Quelle est la puissance fournie à l'ensemble?

b) Si l'un des fusibles de la ligne brûle, quelle sera la nouvelle puissance fournie?

26-12 Si l'un des trois conducteurs d'une ligne triphasée est coupé, la charge devient-elle alimentée par une tension monophasée ou diphasée?

26-13 Un groupe triphasé d'éléments chauffants de 15 kW est alimenté à 208V. Quel est le courant dans chaque ligne?

26-14 On désire charger à pleine capacité, au moyen de résistances, un alternateur triphasé de 100 kVA, 4 kV. Calculer la résistance de chaque élément pour une connexion:

a) en étoile b) en triangle

26-15 Les enroulements d'un moteur triphasé sont raccordés en triangle. On mesure une résistance de 0,6Ω entre deux des trois bornes du moteur. Quelle est la résistance de chaque phase?

26-16 Trois résistances de 24Ω sont raccordées en triangle sur une ligne triphasée à 600V . Calculer la résistance par élément d'un montage en étoile dissipant la même puissance.

26-17 Un moteur triphasé de 45 kW (puissance mécanique) absorbe une puissance active de 50 kW d'une ligne triphasée à 600V. Sachant que le courant dans chaque ligne est de 60 A,

calculer:

a) le rendement du moteur

b) la puissance apparente absorbée par le moteur

c) la puissance réactive absorbée par le moteur

d) le facteur de puissance du moteur

26-18 Trois résistances de 15Ω et trois réactances de 8Ω sont raccordées en étoile selon le schéma de la Fig. 26-12. Sachant que la tension de la ligne est de 530V,

calculer:

a) les puissances active, réactive et apparente fournies à la charge

b) la tension aux bornes de chaque résistance

26-19 Deux lampes de 60W et un condensateur de 10 µF raccordés en étoile sont branchés sur trois bornes triphasées X-Y-Z dont la tension est de 120V. Le condensateur est connecté à la borne Y et la lampe qui brille le plus est connectée à la borne X .

a) Quelle est la séquence des phases?

b) Tracer le diagramme vectoriel des tensions ligne à ligne.

26-20 Deux wattmètres montés dans un circuit triphasé à 220 V indiquent respectivement 3,5 kW et 1,5 kW. Le courant dans chacun des fils de ligne étant de 16 A,

calculer:

a) la puissance apparente de la charge

b) son FP 26-21 Un moteur électrique ayant un FP de 82% tire un courant de 25A d'une ligne triphasée à 600V.

a) Calculer la puissance active fournie au moteur.

b) Sachant que le rendement du moteur est de 85%, quelle puissance en kW développe-t-il?

c) Quelle est sa consommation d'énergie, si le moteur marche pendant trois heures?

26-22 Un wattmètre de 0-3 kW, dont la tension maxi- male est de 300V et le courant maximal de 10A, est inséré dans un circuit dont le FP est de 10% et la tension de 200V. Il indique alors une puissance de 1,7 kW. On s'aperçoit cependant qu'une fumée se dégage du wattmètre au bout de quelques instants. Expliquer.

Niveau avancé

26-23 Trois condensateurs de 10 µF sont montés en étoile sur une ligne triphasée à 2,3 kV, 60 Hz.

a) Quel courant tirent-ils de chaque fil de ligne?

b) Quelle est la puissance réactive fournie par l'ensemble des condensateurs?

26-24 Si dans le problème 26-19, le condensateur est raccordé à la borne X, quelle est la lampe qui brille le plus?

26-25 Trois résistances branchées en triangle sur une ligne triphasée consomment 60 kW.

Quelle sera la puissance absorbée si on les raccorde en étoile?

26-26 Trois résistances de 15Ω et trois réactances de 8Ω sont raccordées symétriquement à une ligne triphasée de 530V selon les montages suivants:

a) R, X en série, connexion en étoile

b) R, X en parallèle, connexion en triangle

c) R en triangle, X en étoile Déterminer pour chaque cas, le courant dans les fils de ligne sans avoir recours aux diagrammes vectoriels (utiliser la méthode des puissances).

26-27 Dans la Fig. 26-13, quel serait le courant dans chaque ligne si la fréquence était de 50 Hz?

26-28 Sur la Fig . 26-7c, la tension E n instantanée est de +100V (valeur projetée sur l'axe vertical).

Quelle est la valeur instantanée des 5 autres tensions?

Copier le schéma de la Fig. 26-7a et indiquer toutes les tensions instantanées avec leurs polarités. D'après la loi de Kirchhoff, la somme des tensions dans une boucle fermée est nulle.

Vérifier que cette loi est bien vérifiée pour ce montage.

26-29 Pour le problème 26-28, la fréquence est de 50 Hz. Déterminer la valeur des tensions instantanées après un intervalle de 1,667 ms.

26-30 Une charge résistive-inductive branchée sur une ligne à 2,4 kV absorbe une puissance apparente de 600 kVA à un FP de 80%. Déterminer les valeurs de R et de X_L en supposant une connexion semblable à celle montrée à la Fig. 26-12.

26-31 Les wattmètres de la Fig. 26-23 indiquent respectivement des puissances de +35 kW et -20 kW. La charge étant équilibrée, calculer :

a) le FP de la charge

b) le courant dans la ligne si la tension triphasée est de 630V

Réponses

1) 4157 V; 2a) E., : + 100; 0; - 50; - 50; + 86,6;
2c) Eb2 : - 50; + 86,6; + 100; - 50; - 86,6; 3) oui; 4a) 358 V;
4b) 23,9 A; 4c) 25,6 kW; 5a) 694 A; 5b) 13,2 kV; 5c) 9,16 MW;
5d) 27,5 MW; 6a) A - C - B ; 7) 26 kVA; 8) 120 V phase-phase;
11 a) 12,9 kW; 11 b) 6,49 kW; 12) monophasée; 13) 41,6 A;
14a) 160Ω; 14b) 480Ω; 15) 0,9Ω ; 16) 8 4; 17a) 90%;
17b) 62,4 kVA; 17c) 37,3 kvar; 17d) 80,1 %;
18a) 14,6 kW; 7,78 kvar; 16,5 kVA; 18b) 270 V; 19a) X - Z - Y;
20a) 6096 VA; 20b) 82% arrière; 21 a) 21,3 kW; 21b) 18,1 kW;
21 c) 63,9 kW h; 23a) 5 A; 23b) 19,9 kvar;
24) lampe raccordée à Z ; 25) 20 kW; 26a) 18 A; 26b) 130 A;
26c) 72,2 A; 27) 18,3 A; 28) Ean = + 100 V; Ebn = - 50 V;
Ecn =-50V;Eab=+150V;Ebc =OV;Eca =-150V;
29) Ean = + 86,6 V; Ebn = 0 V; Ecn = - 86,6 V; Eab = + 86,6 V;
Ebc = + 86,6 V; Eca = - 173,2 V; 30) R = 5,76 S2; XL = 7,68 4;
31 a) 15,6%; 31 b) 88,4 A