Conducteurs
Dans cette section, nous étudierons les propriétés des conducteurs de même que leurs applications. La plupart des conducteurs sont des solides, mais on a vu que dans des conditions spéciales, même un gaz comme l'air peut devenir conducteur.
Certains liquides, comme l'eau salée, peuvent également conduire un courant électrique, de sorte qu'on peut les classer parmi les conducteurs.
Bons conducteurs
De tous les solides, l'argent est le meilleur conducteur d'électricité mais, en raison de son coût prohibitif, son usage est restreint aux contacts destinés à l'ouverture et à la fermeture des circuits électriques. Paradoxalement, il sert aussi comme élément résistif dans certains fusibles.
Dans les applications générales, le matériau le plus employé est le cuivre. On utilise des conducteurs d'aluminium (seuls ou avec des fils d'acier) pour les lignes de transport d'énergie, car, pour une même longueur et un même poids, la résistance électrique de l'aluminium est sensiblement la moitié de celle du cuivre.
Cependant, pour une résistance donnée, son volume est 1,7 fois plus grand que celui du cuivre, ce qui le rend moins intéressant comme conducteur dans les machines électriques. Le bronze phosphoreux se coule très facilement et il est très employé pour les pièces moulées.
Conducteurs résistifs Parmi les matériaux résistifs, les plus importants sont les alliages de nickel et de chrome comme le Ni-chrome Ni-chrome® et le Chromel®.
On les rencontre dans les éléments chauffants de toutes sortes et dans les rhéostats et résistances. Le tungstène est surtout utilisé pour la fabrication des filaments à incandescence à cause de sa haute température de fusion, ce qui permet une chaleur suffisamment intense pour émettre une lumière blanche.
Il existe au moins une trentaine d'autres alliages à base de nickel, de fer, de cobalt et de cuivre portant des noms comme Nilvar®, Advance®, Karma®, Chromax®, Copel®, Ohmaloy®, etc., dont les propriétés particulières telles que la résistance à la corrosion ou la rigidité mécanique les rendent utiles pour les applications spéciales.
Formes des conducteurs
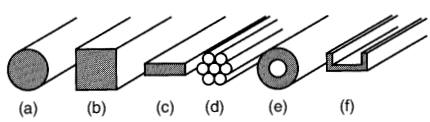
Suivant leurs applications, les conducteurs prennent une grande variété de formes : on les rencontre sous forme de fils de section ronde, carrée ou plate, sous forme de câbles toronnés et sous forme de barres (barres omnibus).
Les conducteurs se présentent généralement sous forme de fils de section ronde (Fig. 10-1 a), obtenus directement par tréfilage.
Les fils bons conducteurs de sections carrée et rectangulaire (Fig. 10-1b, c) sont employés pour les enroulements à grande section des transformateurs et des machines rotatives. L'emploi de tels conducteurs dans les moteurs et génératrices permet une meilleure utilisation du volume des encoches.
Figure 10-1 Diverses formes de conducteurs
Les conducteurs constitués par un grand nombre de petits fils (appelés torons) torsadés ensemble sont très souples (Fig. 10-1 d). La pose des câbles de grande section est ainsi facilitée.
Dans le cas de certains conducteurs d'aluminium, un ou plusieurs fils centraux sont en acier afin d'assurer une plus grande résistance mécanique du câble.
Ces câbles portent le nom ACSR (Aluminum Cable Steel Reinforced»).
Pour les fortes intensités de courant rencontrées dans les centrales et les postes de transformation, on utilise des conducteurs nus de formes particulières qui assurent une meilleure dissipation de la chaleur ou qui possèdent une plus grande rigidité mécanique Fig. 10-1 e, f.
Enfin, on utilise des conducteurs résistifs de sections ronde, carrée et plate dans la fabrication des chaufferettes. des démarreurs de moteurs et des rhéostats.
Mils
On utilise souvent le diamètre pour déterminer le calibre d'un conducteur. La valeur du diamètre est parfois imprimée en mils. Le mil est une unité de longueur anglaise égale à un millième de pouce. Il équivaut à 0.0254 mm ou 25,4 µm.
Circular mil, conducteurs ronds
La valeur de la section droite des conducteurs ronds est souvent exprimée en circular mils. Le circular mil (cmil) est une unité de surface : c'est la surface d'un cercle ayant un diamètre de 1 mil (Fig. 10-2).
Figure 10-2 Un cercle ayant un diamètre de 0,001 pouce possède une surface de 1 cmil
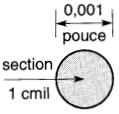
La section droite d'un conducteur circulaire, exprimée en circular mils, est égale au carré de son diamètre en mils.
Le kilocircular mil (kcmil) est une unité de surface égale à 1000 cmil. Noter que l'unité kcmil remplace aujourd'hui l'ancienne unité MCM.
Exprimés en unités métriques:
1 cmil = (0,0254 mm)² x π/4 = 0,000 506 7 mm²
1 kcmil = 1000 cmil = 0,506 7 mm²
Exemple 10-1
Trouver la section droite d'un fil rond ayant un diamètre de 0,102 pouce.
Solution
Le diamètre vaut 102 millièmes de pouce ou 102 mils, donc la section A vaut:
A = 102 mils x 102 mils = 10 404 circular mils = 10,4 kcmil = 10,4 X 0,5067 = 5,27 mm²
Les conducteurs ronds, jauge AWG
Les diamètres des conducteurs ronds sont standardisés.
Au Canada et aux États-Unis on indique le diamètre des conducteurs ronds par un numéro de la jauge «Standard American Wire Gauge», dont l'abréviation est AWG. Le système est aussi connue sous le nom «Brown & Sharpe Gauge» (B & S).
Le système AWG a été conçu en fixant des diamètres de 460 mils et 5 mils respectivement pour les fils #0000 et #36.
Comme il y a 39 intervalles entre #0000 et #36 le rapport entre deux diamètres successifs est de (460/5)1/39 = 1,1229.
Le rapport entre deux sections successives est donc 1,1229² = 1,261.
Selon ce système, le diamètre du fil diminue à mesure que le numéro de jauge augmente. Ainsi, le fil portant le #6 de la jauge est plus petit que le #4.
Le tableau 10-1 donne les propriétés des fils ronds correspondant à chaque numéro de la jauge.
Il est utile de retenir les deux règles suivantes qui s'appliquent au système AWG:
1. Un conducteur qui a deux fois la section d'un autre porte un numéro qui est plus petit de 3 unités.
Exemple: la section du fil #5 est le double de celle du fil #8.
2. Un conducteur qui a 10 fois la section d'un autre porte un numéro qui est plus petit de 10 unités.
Exemple: le fil #4 a la même section que 10 fils #14.
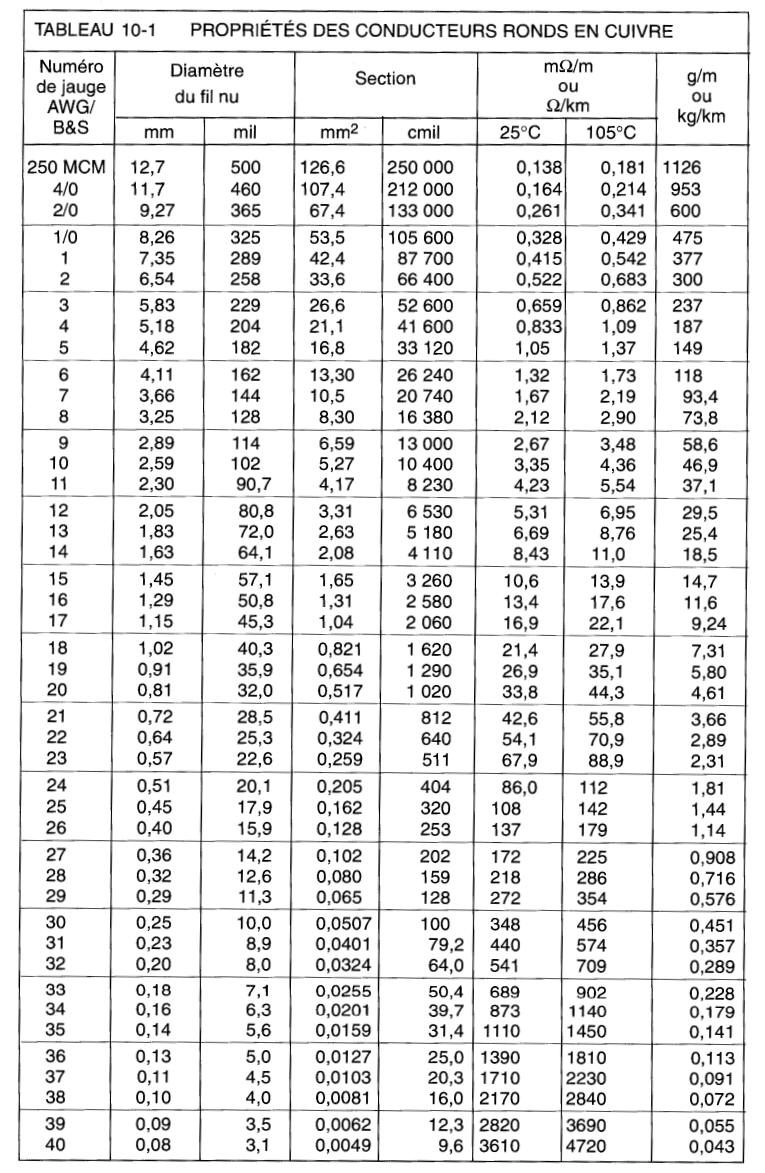
La Fig. 10-3 indique comment on mesure le calibre d'un conducteur au moyen d'une jauge. Tout isolant, y compris le vernis, doit être enlevé; le fil nu doit être inséré dans l'encoche et non dans l'ouverture circulaire de la jauge.
Figure 10-3 Mesure de la grosseur d'un conducteur avec une jauge AWG.
Un conducteur nu #4 peut se glisser dans l'ouverture 4 de la jauge. La jauge et ses ouvertures (numérotées de 0 à 36) sont montrées grandeur nature
Câbles toronnés
La section droite d'un câble toronné est également exprimée en millimètres carrés ou en circular mils : elle est égale à la somme des sections de chacun des torons et ne comprend pas la surface des interstices.
Un fil #10 toronné, habituellement formé de 7 conducteurs d'un diamètre de 38,54 mils (1486 cmils), a donc rigoureusement la même résistance qu'un fil #10 plein qui a une section de 10 400 cmils.
Pour les conducteurs qui ont une section plus grande que celle correspondant au 0000 (habituellement désignée 4/0), on indique généralement la section en milliers de circular mils (kcmil).
Ainsi, un conducteur de 250 kcmil ne correspond à aucun numéro de jauge.
Fils de section carrée
L'usage veut que les fils de section carrée portent des numéros correspondant à ceux des fils ronds. Si le côté du fil carré est égal au diamètre du fil rond, les deux porteront le même numéro (Fig. 10-4).
Figure 10-4 Dimensions d'un conducteur carré #10 et d'un conducteur rond #10
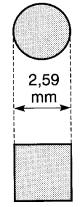
Par conséquent, la section d'un fil carré est environ 25 % plus grande que celle d'un fil rond portant le même numéro.
Résistance d'un conducteur À une température donnée, la résistance d'un conducteur dépend:
1. de sa longueur
2. de sa section
3. de la nature de la substance qui le constitue
Nous avons vu que le passage du courant dans un conducteur est analogue à l'écoulement de l'eau dans un tuyau.
On remarque par expérience que plus le tuyau est long, plus sa résistance au passage de l'eau est grande. De même en électricité, plus le conducteur est long, plus sa résistance au passage du courant est grande.
Si l'on remplace le tuyau par un autre ayant une plus grande section, le passage de l'eau se fait plus librement, sa résistance est réduite.
Il en est ainsi pour un conducteur électrique: plus sa section est grande, plus son opposition (résistance) au passage du courant est faible.
Le passage du courant électrique dans un conducteur se fait d'autant plus facilement que le nombre d'électrons libres est grand.
Or, ce nombre d'électrons libres varie considérablement d'une substance à l'autre.
Donc, la résistance au passage du courant dépend de la nature de la substance dont est constitué le conducteur ; plus le nombre d'électrons libres est grand, plus la résistance est basse.
La formule qui donne la relation entre la résistance d'un conducteur et les trois facteurs énumérés plus haut est la suivante:
R = ρ (l/A) (10-1)
où
R = résistance du
conducteur, en ohms [Ω]
ρ = résistivité de la substance, en ohm-mètres [Ω.m]
l = longueur du conducteur, en mètres [m]
A = section du conducteur, en mètres carrés [m²]
Ce facteur p qu'on appelle résistivité est précisément ce qui caractérise l'opposition plus ou moins grande qu'offre un conducteur au passage du courant. Il varie suivant la nature de la substance dont est constitué le conducteur. Elle varie aussi avec la température.
Tout comme la masse volumique, la résistivité est une propriété caractéristique d'une substance.
Bien que l'unité SI de résistivité soit l'ohm-mètre (Ω.m), nous utilisons plutôt un sous-multiple, soit le nanohm-mètre (nΩ.m) valant 10-9 Ω.m pour décrire la résistivité des conducteurs. On trouvera au tableau 10-2, la valeur de la résistivité de quelques-uns des métaux usuels.
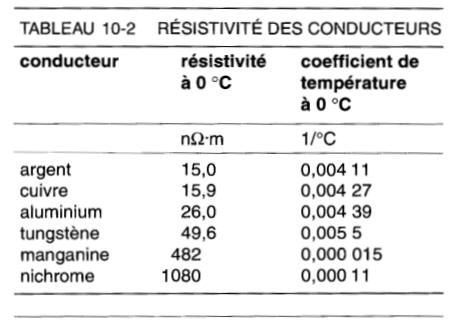
Le tableau 10-5 en fin de cette section fournit une liste plus complète.
Exemple 10-2
Calculer la résistance d'un conducteur de cuivre ayant une longueur de 2 km et une section de 67 mm² (Fig. 10-5).
Figure 10-5 Ligne de transport de 2 km
La résistivité du cuivre vaut 18 nΩ.m
Solution
En exprimant toutes les unités en mètres et en mètres carrés on obtient:
R = ρ (l/A) = 18 x 10-9 x (2000 / 67 x 10-6)= 0,53752
Exemple 10-3
Calculer la résistance d'un Fil #20 B & S en nichrome ayant une longueur de 25 mètres, à une température de 0"c.
Solution
D'après le tableau 10-1, la section d'un conducteur rond #20 vaut 0,517 mm².
La résistivité du nichrome à 0 °C étant de 1080 nΩ.m (tableau 10-2), la résistance R du conducteur est donnée par:
R = ρ (l/A) = 1080 x 10-9 x (25 / 0,517 x 10-6) = 52,2Ω
Variation de la résistance avec la température
Lorsque la température d'un conducteur augmente, l'agitation de ses atomes s'accentue. L'opposition au déplacement des électrons (courant) augmente parce que les collisions entre les électrons et les atomes se multiplient. C'est ce qui explique l'augmentation de la résistivité des métaux conducteurs avec la température.
Cette variation obéit à la formule suivante:
ρr = ρ0 (1 + αt) (10-2a)
ou
ρr = résistivité
à une température t, en ohm-mètres [Ω.m]
ρ0 = résistivité à 0 °C, en ohm-mètres [Ω.m]
α = coefficient de température, en 1/°C
t = température, en °C
Pour le cuivre, a = 0,004 27.
On trouvera au tableau 10-2, la valeur de ce coefficient pour quelques-uns des métaux usuels. Puisque la résistivité varie avec la température, il s'ensuit que la résistance de tout dispositif électrique (bobine, fil, câble, élément chauffant, etc.) varie en proportion.
On peut donc exprimer la variation de la résistance par la formule:
Rt = R0 (1 + αt) (10-2b)
où
Rt = résistance à une
température t, en ohms
R0 = résistance à 0 °C, en ohms
α = coefficient de température, en 1/°C
t = température, en °C
Exemple 10-4
Trouver la variation de la résistance d'une ligne de transport d'énergie entre des températures de -30 °C et +35 °C, si la résistance des conducteurs de cuivre est de 100 mΩ ( milliohms ) à 0 °C
Solution
La résistance du conducteur à -30 °C est donnée par:
Rt = R0 (1 + αt)
R-30°C = 100 (1 + (0,00427 x -
30)) = 100 (1 - 0,128) = 100 (0,872) = 87 mΩ
À 35 °C, la résistance
deviendra:
R35°C = 100 (1 + (0,00427 x 35)) = 100 (1 + 0,149) = 115 mΩ
La résistance de la ligne augmentera de 87 mΩ à 115 mΩ, soit une variation d'environ 30 % de 87 mΩ.
Pour le même courant, les pertes dans la ligne électrique peuvent donc être plus élevées de 30 % pendant les chaleurs d'été que pendant les froids d'hiver.
L'augmentation de la résistance est encore plus remarquable pour le filament d'une lampe à incandescence dont la température de fonctionnement est très élevée.
En marche normale, le filament de tungstène possède une résistance d'environ 12 fois plus élevée à chaud qu'à froid.
Exemple 10-5
Une lampe à incandescence de 60 watts possède une résistance de 17,6 S2 à 20 '°C (Fig. 10-6).
Figure 10-6 La résistance d'une lampe à incandescence dépend de sa température
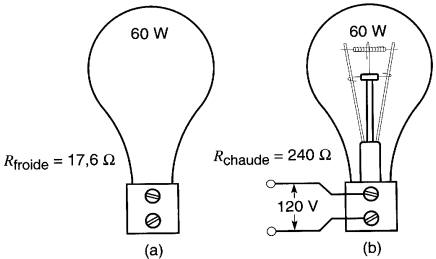
Si elle tire un courant de 0,5A sous une tension de 120 V, quelle est la température du filament?
Pour le tungstène : α = 0.0055 par °C.
Solution
Il faut d'abord calculer la résistance du filament à 0 °C.
Rt = R0 (1 + αt)
17,6 = R0(1 + 0,0055 x 20) = R0(1,11)
d'où R0 = 15,85Ω
Résistance à chaud = E/I = 120 V/0,5 A = 240 Ω.
En utilisant à nouveau la formule (10-2b) et en appelant t la température cherchée, on obtient:
240 = 15,85 (1 + 0,0055 t)
d'où t = 2571 °C
La résistance de certains alliages comme le constantan et le manganine ne varie presque pas avec la température; c'est pourquoi on les utilise dans la fabrication des résistances étalons et des shunts d'ampèremètres.
D'autres alliages à base de nickel et de chrome, comme le nichrome et le chromel, possèdent une haute résistivité et un bas coefficient de température ce qui permet la construction d'éléments résistifs économiques dont la résistance varie peu avec la température.
Ainsi, la résistance du nichrome V n'augmente que de 7 % lorsque sa température passe de 20 °C à 1000 °C.
PROPRIÉTÉS MÉCANIQUES DES CONDUCTEURS
Résistance à la traction
Jusqu'ici, nous nous sommes intéressés aux propriétés électriques et thermiques des conducteurs, mais dans certains cas on doit considérer également leurs propriétés mécaniques.
Par exemple, la résistance des conducteurs à la traction joue un rôle important lors de la pose des lignes aériennes et du bobinage des enroulements.
D'abord, il ne faut pas que la tension subie par le conducteur dépasse la tension de rupture.
On ne doit pas non plus provoquer un allongement tel que le conducteur ne puisse plus reprendre sa longueur et sa forme originales.
Ces deux considérations demandent une connaissance des forces qui peuvent changer sa longueur de façon permanente.
Traction et allongement
Si l'on augmente la force de traction F exercée sur un fil métallique, tout en observant son allongement d(Fig. 10-7), on obtient une série de valeurs que l'on peut porter sur un graphique (Fig. 10-8).
Figure 10-7 Allongement d d'un conducteur
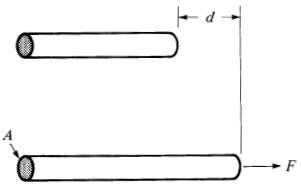
Figure 10-8 Allongement d'un fil en fonction de la force de traction
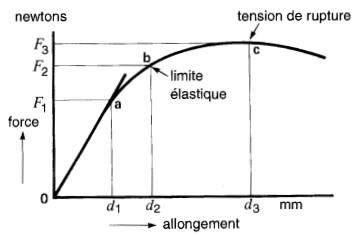
Sur cette courbe, nous avons indiqué trois points importants a, b et c, correspondant respectivement aux forces de traction F1, F2 et F3. À mesure que la force de traction croît de 0 à F1, le fil s'allonge d'une distance dl.
Dans la partie droite Oa de la courbe, l'allongement d est proportionnel à la traction exercée et le fil se comporte comme un ressort. Il reprend sa forme originale dès que la traction cesse.
Pour des tractions F supérieures à F1, mais inférieures à F2, le fil perd un peu de son élasticité et il ne revient pas à sa longueur originale lorsque la traction cesse. Cependant, l'étirement permanent n'est pas sérieux ni dommageable. La force F2 au point b correspond à la limite élastique; on évite, en général, de dépasser cette force plus ou moins bien définie.
Si l'on continue à augmenter la traction, le fil s'étire rapidement jusqu'au point c situé au sommet de la courbe; la tension F3 correspondante est la tension de rupture et elle est sensiblement supérieure à la force F,.
Au-delà du point C, une force même inférieure à F3 réussit à étirer le conducteur jusqu'à sa rupture complète.
Tous les conducteurs possèdent de telles courbes de traction mais les forces F1, F2 et F3 varient beaucoup suivant le métal. La forme de la courbe dépend aussi de la température, les forces devenant plus petites et l'allongement plus grand quand la chaleur augmente.
Enfin, la valeur des forces varie beaucoup suivant que le conducteur a été formé à froid, à chaud ou qu'il a été recuit.
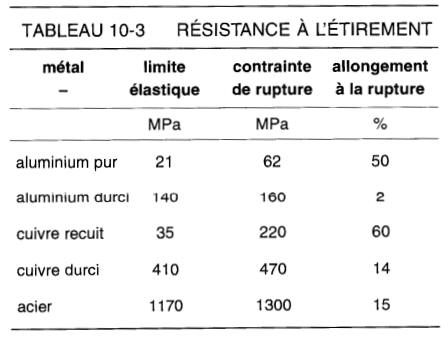
Soit A la section de l'échantillon initial. On appelle limite élastique («field strength»), le rapport F1/A exprimé en mégapascals (MPa) et contrainte de rupture «tensile strength» le rapport F3/A exprimé en MPa.
Les catalogues donnant la résistance des matériaux fournissent en général ces deux valeurs, ainsi que l'allongement à la rupture en pour cent (voir les tableaux 10-3 et 10-5). En observant les valeurs fournies pour le cuivre recuit, on constate que la limite élastique est de 35 MPa, que la contrainte de rupture est de 220 MPa et que le fil s'allonge de 60 % avant que ce point de rupture soit atteint.
Le tableau 10-3 illustre aussi la grande différance entre le cuivre recuit et le cuivre durci. Le premier est utilisé pour les bobines, tandis que le second trouve son application dans les lignes aériennes.
Exemple 10-6
Quelle force de traction peut-on appliquer à un fil de cuivre #12 recuit sans provoquer un allongement appréciable, et quelle force de traction provoque la rupture?
Si le fil a une longueur initiale de 100 mètres, quelle sera sa longueur au moment de la rupture?
La section du fil #I2 = 3.31 mm².
Solution
La limite élastique étant de 35 MPa, la tension permise est:
F2 = (limite élastique) x (section) = (35 X 106 Pa) x (3,31 x 10-6 m²) = 116 newtons = 116 N
La tension de rupture sera:
F3 = (contrainte de rupture) x (section) = (220 x 106 Pa) x (3,31 x 10-6 m²) = = 728 newtons = 728 N
Enfin, l'allongement à la rupture étant de 60 %, le fil s'étirera de: 100 m x 60 % = 60 m.
Il atteindra donc une longueur approximative de 160 m lors de la rupture.
La Fig. 10-9 montre deux types de câbles en aluminium utilisés dans les lignes aériennes. Le premier est composé entièrement de torons en aluminium, alors que le deuxième comprend une âme en acier. La tension de traction permise est beaucoup plus grande pour le deuxième câble.
Figure 10-9
a. Câble nu en aluminium, 500 kcmil, composé de 37 torons, ayant chacun un diamètre de 2,951 mm. Le diamètre du câble est de 20,6 mm. La charge de rupture est de 40 kN ; courant admissible : 640 A.
b. Câble nu du type ACSR, 500 kcmil, composé de 37 torons dont 30 sont en aluminium et 7 en acier, ayant tous un diamètre de 3,279 mm. La charge de rupture est de 130 kN; courant admissible: 690 A.
Dans le cas des lignes de transport, on comprend facilement pourquoi on doit renforcer un câble d'aluminium avec une âme en acier. En effet, l'aluminium ne possède pas la résistance à la traction requise pour les câbles de longue portée.
ISOLEMENT DES CONDUCTEURS
Types d'isolants
La plupart des conducteurs sont recouverts d'un isolant afin d'empêcher le courant de passer d'un conducteur à un autre ou pour éviter les mises à la terre.
L'isolement des conducteurs utilisés dans les machines électriques est souvent assuré par du coton, de la soie ou du papier imprégnés de vernis spéciaux.
Aujourd'hui on utilise de plus en plus des isolants synthétiques pour les machines de moyenne et de grosse capacités. Les conducteurs utilisés dans les maisons, les usines et les immeubles pour la distribution de l'électricité sont isolés par des isolants souples : caoutchouc, papier, coton, cambric et produits thermoplastiques.
Ces conducteurs doivent fonctionner à des températures peu élevées afin de leur assurer une durée de vie très longue. L'isolant à polyéthylène réticulé chimiquement, souvent connu sous le nom XLPE (cross-linked polyethylene), dont la rigidité diélectrique est aujourd'hui entre 13 et 15 kV/mm, permet la construction de câbles allant jusqu'à 400 kV.
La température maximale de 250 °C constitue un autre avantage pour résister aux chocs thermiques provoqués par des court-circuits. Les fils exposés aux hautes températures des fours électriques doivent être recouverts d'un isolant d'origine minérale.
Le verre, l'amiante, la porcelaine et le mica supportent très bien, sans détérioration appréciable, des températures très élevées. Cependant, leur application est limitée du fait de leur coût élevé et parce qu'ils sont difficiles à manipuler.
Capacité thermique des conducteurs
Étant donné que même les meilleurs conducteurs ont une certaine résistance, ils s'échauffent par effet Joule lorsqu'ils sont parcourus par un courant. Dans le cas des conducteurs nus, si la température atteinte est trop élevée, il peut y avoir risque de fusion ou de détérioration des parties voisines du conducteur.
Le conducteur peut lui-même se désagréger par oxydation excessive.
Pour les conducteurs isolés, la chaleur produite doit être transmise par les couches isolantes et ensuite dispersée par radiation et par convection. Plus l'intensité du courant dans le fil est grande, plus grande est l'élévation de température de l'isolant. Pour assurer une durée de vie convenable à l'isolant, il est donc nécessaire de limiter le courant que peut porter un fil isolé.
On arrive ainsi à une conclusion importante qui s'applique presque toujours : le courant maximal admissible dans un fil isolé est fixé par la température maximale admissible de son isolant.
Code régissant les installations électriques
La durée de vie des conducteurs servant à la distribution de l'électricité dans les usines, les édifices et les maisons est particulièrement importante, car on ne peut pas se permettre de changer les fils dans les murs tous les dix ans.
Pour cette raison, le Code canadien de l'électricité exige des températures maximales particulièrement basses pour les conducteurs employés dans les installations électriques. Selon le type d'isolant, les normes permettent des températures maximales de 60 °C, 75 °C et 90 °C.
Elles sont beaucoup plus basses que les températures maximales admises dans les appareils électriques (moteurs, transformateurs, etc.) utilisant le même genre d'isolant. Aux endroits particulièrement chauds, on doit faire courir du fil isolé en amiante; on peut alors se permettre des températures maximales aussi élevées que 200 °C.
Un conducteur doit dégager sa chaleur dans l'air environnant et, afin d'établir le courant admissible, le Code canadien de l'électricité définit une température ambiante standard de 30 °C.
Sachant que la température ambiante est fixée à 30 °C et que la température d'un conducteur quelconque ne doit pas dépasser une certaine valeur limite (disons 75 °C), le Code spécifie le courant maximal que ce conducteur peut supporter.
Par exemple, le Code stipule qu'un fil #6 à l'air libre, recouvert d'un isolant thermoplastique (type TW), dont la température nominale est de 60 °C peut supporter un courant nominal de 80 A (Fig. 10-1 Oa).
Par ailleurs, le Code stipule que le même conducteur isolé au silicone/caoutchouc (type SRK) peut supporter un courant de 125 A (Fig. 10-10b).
Figure 10-10 Comparaison de la capacité ampérique de deux conducteurs de même section
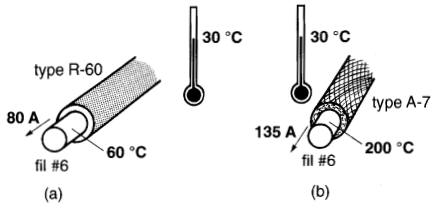
Bien que sa température nominale soit alors de 200 °C, sa durée de vie sera la même que celle du conducteur TW qui aura supporté seulement 60 °C.
Le tableau 10-4, tiré du Code canadien de l'électricité, donne un aperçu des courants admissibles pour les divers types de monoconducteurs, lorsqu'ils sont suspendus seuls, à l'air libre, à une température ambiante de 30 °C.
Lorsque plusieurs conducteurs isolés sont placés dans un même tuyau métallique (conduit), la chaleur dégagée par chacun contribue à l'échauffement de l'isolant des conducteurs voisins. Le courant doit donc être plus faible que si le conducteur était seul, afin de ne pas dépasser la température permise pour l'isolant.
Par exemple, le Code spécifie que trois conducteurs #4, type TW60, placés dans un conduit ne doivent porter que 70 A chacun, alors qu'il permet un courant de 105 A pour un conducteur seul.
Comparaison de divers conducteurs
Les câbles montrés dans les Fig. 10-11 à 10-18 donnent une idée de la construction adoptée selon les tensions qu'ils peuvent supporter et l'usage qu'on en fait. Les vues en coupe sont dessinées grandeur nature afin que le lecteur puisse mieux apprécier les dimensions physiques de ces câbles.
Figure 10-11 a. conducteurs isolé à l'amiante b. conducteurs isolés et recouverts d'une gaine métallique c. conducteurs sous plomb
Un examen détaillé de ces figures révèle l'information suivante :
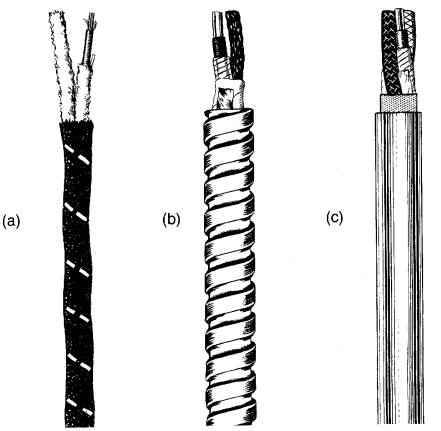
1. Une augmentation de la tension de 5 kV à 30 kV exige une plus grande quantité d'isolation, donc un câble plus gros. Par ailleurs, la capacité ampérique n'est pas affectée de façon appréciable (comparer les Fig. 10-12a et 10-12b).
2. Un câble à 30 kV possédant un conducteur en aluminium a une capacité de 343 A alors qu'un câble semblable en cuivre peut supporter 440 A (comparer les Fig. 10-12b et 10-12e).
3. Un câble à 30 kV formé de 3 conducteurs en cuivre a une capacité de 359 A par conducteur au lieu de 440 A pour un câble ayant un seul conducteur (comparer les Fig. 10-12b et 10-13).
4. Pour une même tension de 600 V, une isolation R90 au polyéthylène réticulé (XLPE) est plus mince qu'une isolation RW60. De plus, la capacité ampérique est plus élevée (Fig. 10-14).
5. Le câble sous-marin à 80 kV, 630 A est plus gros que celui à 30 kV, 343 A, car il est protégé par une lourde gaine d'acier, et parce qu'il transporte une plus grande puissance (comparer les Fig. 10-12c et 10-15).
Figure 10-12 Capacité ampérique à l'air libre de trois conducteurs ayant une section de 250 kcmil (grandeur nature)
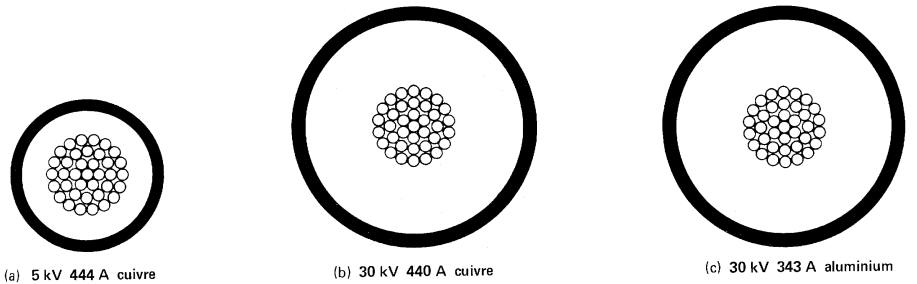
Figure 10-13 Câble triphasé formé de trois conducteurs de section 250 kcmil (grandeur nature)
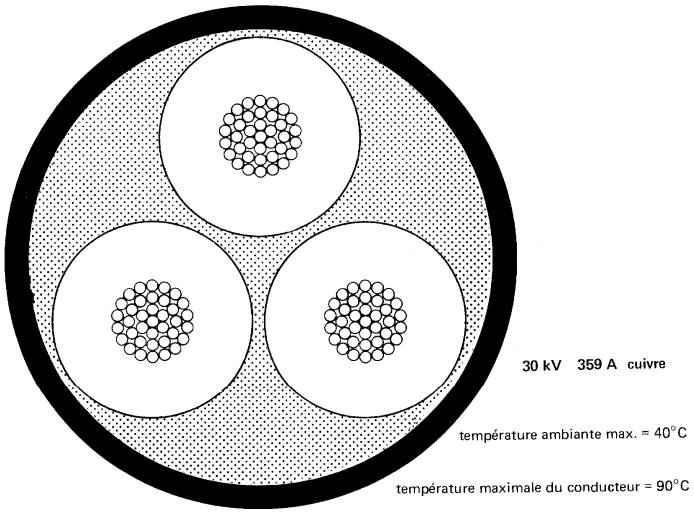
Figure 10-14 Deux conducteurs isolés à 600 V (grandeur nature)
Figure 10-15 Vu en coupe d'un câble sous-marin, grandeur nature. Diamètre extérieur 70 mm. Ce câble est immergé dans le détroit de Long Island entre Northport (Long Island) et Norwalk (Connecticut)
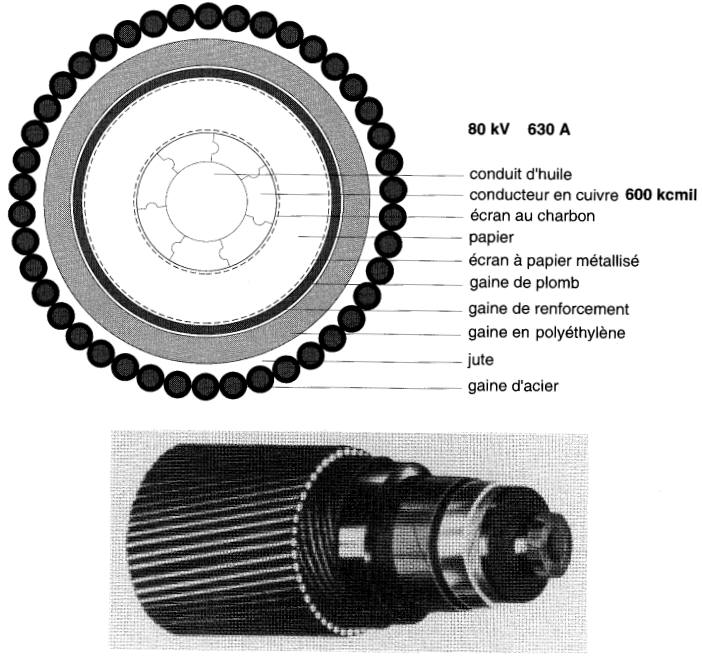
Figure 10-16 Câble d'alimentation pour pompe submersible utilisé dans les mines. Il comprend trois conducteurs de puissance, deux de commande et un de mise à la masse.
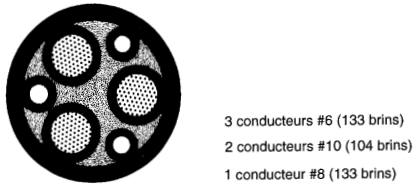
Figure 10-17 Câble ultra-flexible de 600 A pour soudeuse électrique
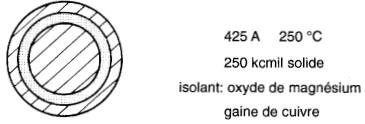
Figure 10-18 Câble pour usage dans les endroits très chauds
Échauffement rapide des conducteurs - facteur I²t
Il arrive parfois qu'un courant beaucoup plus grand que le courant normal circule dans un conducteur durant une courte période. Les pertes Joule sont alors très grandes, de sorte que la température du conducteur peut monter de plusieurs centaines de degrés en une fraction de seconde.
Par exemple, lors d'un court-circuit, des courants intenses circulent brièvement dans les fils et câbles d'un réseau avant que le circuit soit ouvert par un fusible ou un disjoncteur de protection.
Dans ces circonstances, la chaleur dégagée dans les conducteurs n'a pas le temps de se dissiper à travers les parois extérieures et la température du conducteur monte rapidement.
Quel est l'échauffement dans ces conditions?
Supposons que le conducteur ait une masse m, une résistance R et une chaleur massique c. De plus, supposons qu'il porte un courant I durant une courte période t, où t est généralement inférieure à 15 secondes.
La chaleur Q générée dans le conducteur est donc :
Q = RI²t (10-3)
En utilisant l'équation 1-17, on peut calculer la valeur de l'échauffement θ
Q=mcθ éq. 1-17
donc
RI²t = Q=mcθ
d'où
θ = (R / mc) I²t (10-14)
Il s'ensuit que pour un conducteur donné l'échauffement 0 dépend
directement du facteur I²t. Ce facteur s'exprime en ampères carrés seconde
(A².s).
Nous avons vu que des températures élevées sont dommageables pour l'isolant qui recouvre le conducteur.
Le facteur I²t est donc très important car c'est lui qui détermine la température maximale du conducteur.
Par exemple, un conducteur #2 en cuivre initialement à 90 °C ne peut supporter un I²t supérieur à 22 x 106 A².S si l'on veut limiter sa température à 250 °C lors d'un court-circuit.
De façon générale, on peut calculer la valeur de I²t lorsqu'on connaît
(1) le calibre du conducteur, (2) sa composition (cuivre ou aluminium) et (3) l'échauffement qu'il doit subir.
La valeur de I²t pour le cuivre et l'aluminium est donnée par les équations suivantes:
pour le cuivre:
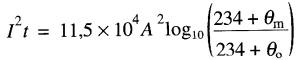(10-15)
pour l'aluminium:
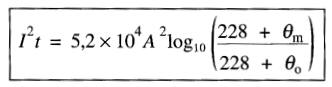
où
I = courant de court-circuit [A]
t = durée du court-circuit [s]
A = section nette du conducteur, sans compter les espaces vides [mm2]
θo = température initiale du conducteur [°C]
θm = température finale du conducteur [°C]
Exemple 10-7
Une ligne aérienne en aluminium est composée d'un conducteur #3 ayant une section de 26.6 mm². Ce conducteur peut supporter un courant de 160 A en régime permanent.
a) Calculer la valeur permissible de I²t lors d'un court-circuit sachant que la température initiale est de 80°C et que l'on désire limiter la température maximale à 250°C ?
On prévoit un courant de court-circuit de 2000 A.
Pendant combien de temps ce courant peut-il circuler sans dépasser le seuil de 250°C ?
Solution
a) En utilisant l'équation 10-6 on obtient :
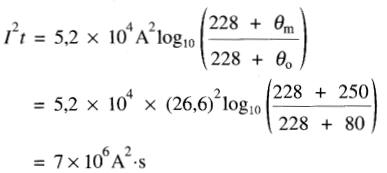
b) Le courant de 2000 A peut circuler pendant un temps r donné par:
I²t = 7x 106
(2000)² t = 7 x 106
t = 1,75 s
Exemple 10-8
On se propose d'utiliser un fil de cuivre #30 comme fusible. Si la température initiale du fil est de 50 °C calculer:
a) le I²t requis pour faire fondre le fil (la température de fusion du cuivre est de 1083°C)
b) le temps requis pour faire fondre le fil si le courant de court-circuit est de 30A
Solution
a) En utilisant le tableau 10-1 on trouve:
A = 0,0507 mm², et de l'équation 10-5 on obtient :
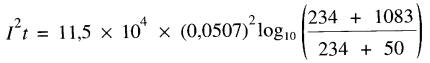
= 197 A².s
on a I²t = 197
(30)² t = 197
t = 0,22 s
Donc le fusible «saute» 220 ms après que le courant de 30 A commence à circuler.
Le rôle des fusibles
Afin de protéger un conducteur contre les températures excessives occasionnées par des courts-circuits, on place un fusible en série avec le conducteur. Le fusible doit être conçu afin que son facteur I²t de fusion soit inférieur à celui qui provoque une surchauffe du conducteur.
En effet, on veut que le fusible brûle avant que le conducteur atteigne une température excessive, ordinairement de l'ordre de 250 °C.
En pratique, le I²t du fusible est bien inférieur à ce seuil. Cependant, le I²t du conducteur demeure un critère important dans le choix du fusible.
Conducteurs liquides, électrolytes
Les métaux tels que le mercure, le plomb, le fer, etc., contiennent autant d'électrons libres à l'état liquide qu'à l'état solide, de sorte que sous ces deux formes ils sont de bons conducteurs de l'électricité.
Cependant, un liquide comme l'eau pure est un excellent isolant avec une résistivité 1012 fois plus grande que celle du cuivre.
Mais, si on ajoute à un litre d'eau quelques cuillerées de sel de table, on constate que sa résistivité diminue des dizaines de fois ; pourtant le sel, est lui-même un excellent isolant.
Comment le mélange d'un isolant liquide et d'un isolant solide peut-il donner une solution conductrice?
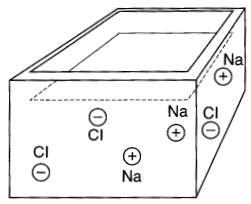
En présence de l'eau, chaque molécule de sel, formée d'un atome de sodium (Na) et d'un atome de chlore (Cl), se sépare en deux pour former un ion (+) de sodium et un ion (-) de chlore.
L'ion de sodium est un atome de sodium ayant perdu un électron, tandis que l'ion de chlore est un atome de chlore possédant un électron en trop.
Ces ions se déplacent de façon désordonnée à l'intérieur de la solution aqueuse, un peu comme les électrons libres à l'intérieur d'un métal.
Puisque les charges portées par les ions positifs et négatifs sont égales, la solution est, dans son ensemble, électriquement neutre (Fig. 10-19).
Figure 10-19 Ions positifs et négatifs
Si l'on plonge deux électrodes raccordées à une pile dans cette solution (appelée électrolyte), les ions (+) et (-) se dirigent respectivement vers les plaques de polarité opposée (Fig. 10-20).
Figure 10-20 Migration des ions
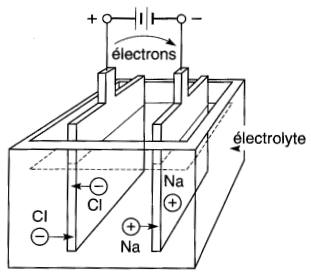
Dès qu'un ion positif (Na+) touche la plaque négative, il capte un électron libre à l'intérieur de cette électrode et devient un atome de sodium neutre.
De la même façon, chaque ion négatif (Cl-) touchant la plaque positive libère son électron en surplus pour devenir un atome de chlore neutre.
Il s'établit ainsi un courant électrique dans le circuit formé par l'électrolyte, les électrodes et la batterie.
Cependant, on constate que le courant dans l'électrolyte n'est pas composé d'électrons mais d'ions positifs et négatifs se déplaçant respectivement vers la droite et vers la gauche. Dans la batterie, les électrons circulent de la borne (+) à la borne (-).
Le même phénomène se produit lorsqu'on mélange avec de l'eau d'autres sels tels que le sulfate de cuivre, ou des acides tels que l'acide sulfurique.
L'électrolyte ainsi formé est rempli d'ions positifs et négatifs représentant chacun un atome (ou une molécule) ayant perdu ou gagné un ou plusieurs électrons.
Habituellement, il se produit une réaction chimique aux deux électrodes car les atomes libérés par la neutralisation des ions réagissent souvent avec l'eau ou la plaque avec laquelle ces ions viennent en contact. Il se dégage alors des gaz autour des électrodes ou, encore, la plaque se dissout à mesure que le courant électrique circule.
Dans certains cas, les atomes libérés à une plaque adhèrent sur celle-ci et forment une couche qui devient de plus en plus épaisse à mesure que le courant circule. Ce procédé, appelé galvanoplastie, permet de recouvrir des objets conducteurs avec un dépôt métallique.
Exemple 10-9
Deux électrodes ayant une surface de 1,2 m² sont plongées dans de l'eau de nier dont la résistivité est de 0.3 Ω.m
Si la distance entre les plaques est de 10 cm, calculer la valeur approximative du courant lorsqu'on applique une tension de 10 V entre les électrodes.
Solution
La résistance de l'électrolyte est:
R = ρ(l/A) éq.10-1
= 0,3 Ω.m x (0,1 m / 1,2 m²) = 0,025 ohm
Le courant vaut donc I = E/R = 12/0,025 = 480 A
On constate que, même si la résistivité de l'eau salée est 20 millions de fois plus grande que celle du cuivre, le courant qui circule est tout de même appréciable.
Résistance du sol
La résistance du sol joue un rôle extrêmement important dans les installations électriques.
D'abord, pour des raisons de sécurité du personnel et de l'équipement, tous les réseaux électriques sont raccordés à la terre ( «mise à la terre»).
Ensuite, certaines lignes haute-tension à c.c. utilisent parfois la terre comme conducteur de retour portant des courants de plusieurs centaines d'ampères.
Enfin, comme le sol est un assez bon conducteur, il offre un chemin à des courants de fuite de toutes sortes qui peuvent provoquer la corrosion des tuyaux métalliques enfouis dans la terre.
La résistivité du sol se situe entre 5Ω.m et 5000Ω.m selon la composition de la terre (argile, sable, granit. etc.) et son degré d'humidité.
Par exemple, au printemps, la résistivité du sol mouillé peut être de 50Ω.m alors que pendant la sécheresse d'été, elle peut grimper à 300Ω.m. Remarquer que la résistivité du sol est plusieurs millions de fois plus grande que celle du cuivre.
Résistance entre deux électrodes de terre
Malgré sa haute résistivité, le sol devient un excellent conducteur grâce à la section presque sans limite qu'il offre au passage du courant.
Par exemple, si l'on applique une tension E à deux électrodes de terre piquées dans le sol, on constate que le courant s'étend à travers tout le volume de la terre en suivant le chemin de la Fig. 10-21.
Figure 10-21 Courant et résistance de terre
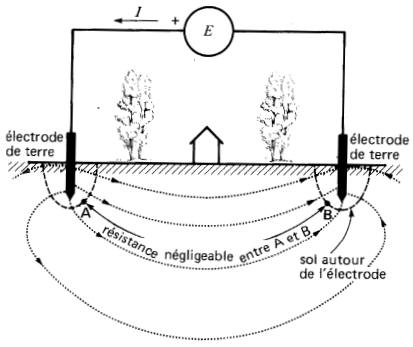
La résistance mesurée entre les deux électrodes demeure relativement faible, même si elles sont distantes de plusieurs centaines de kilomètres.
On peut distinguer 4 résistances sur le circuit de la Fig. 10-21 :
1. résistance des électrodes mêmes - négligeable;
2. résistance de contact entre les électrodes et le sol - négligeable;
3. résistance du sol dans les zones A et B entourant les électrodes respectives - importante;
4. résistance du sol entre les zones A et B - négligeable.
La résistance (3) dépend surtout de la nature du sol et de la profondeur à laquelle les électrodes sont enfoncées dans le sol. L'expérience montre que la résistance est surtout concentrée dans un rayon de 10 mètres autour de chaque électrode.
Au delà de ce rayon, la résistance est négligeable. Par conséquent, la distance séparant les électrodes ne change pas la résistance entre elles, à moins qu'elles soient très rapprochées.
On peut réduire la résistance (3) en enfonçant davantage l'électrode dans le sol, ou en imbibant ce dernier d'un produit chimique, tel que le sulfate de cuivre. En général, la résistance diminue de moitié chaque fois que la profondeur augmente d'un facteur de 1,7.
Par exemple, si une profondeur de 1 m donne une résistance de 80Ω, une profondeur de 1,7 m donnera une résistance de 40Ω.
Mesure de la résistance d'une électrode de terre
On peut mesurer la résistance d'une électrode A, enfoncée d'une profondeur h dans le sol, en utilisant le montage de la Fig. 10-22.
Figure 10-22 Mesure de la résistance d'une électrode de terre
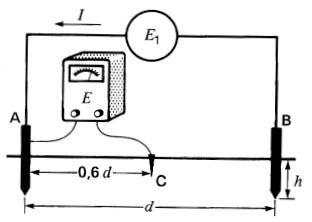
Voici la procédure à suivre :
1) On enfonce dans le sol, à la même profondeur, une deuxième électrode B, située à une distance d de l'électrode A. Cette distance doit être au moins 10 fois plus grande que la profondeur h.
2) À partir de l'électrode A, on plante une tige métallique C située à une distance de 0,6d de celle-ci, et en ligne avec l'électrode B.
3) On applique une tension Et entre les électrodes A et B, et on mesure le courant I qui en résulte.
4) On mesure la tension E entre la tige C et l'électrode A.
5) Le rapport E/I donne la résistance du sol au voisinage de l'électrode A.
On dit tout simplement que c'est la résistance de l'électrode A.
Il existe des instruments spéciaux pour mesurer la résistance d'une électrode (Fig. 10-23), mais la méthode simple que nous venons de décrire donne une précision acceptable pour autant que les lectures soient prises loin des installations électriques.
Figure 10-23 Ohmmètre («megger») pour mesurer la résistance de terre.
Un générateur interne génère une tension maximale de 30 V à une fréquence de 128 Hz. Cette fréquence assure que la lecture de la résistance ne sera pas affectée par des courants parasites de 50 Hz et 60 Hz circulant dans le sol.
Les échelles de 20Ω, 200Ω et 2 kΩ produisent respectivement des courants efficaces de 10 mA, 1 mA et 0,1 mA.
Exemple 10-10
Deux électrodes A et B séparées de 40 m sont enfoncées à une profondeur de 80 cm dans un champ. Une source de tension E1 appliquée entre les électrodes y fait circuler un couvant de 0,2 A.
On mesure une tension E de 19 V à une distance de 60% x 40 = 24 m de l'électrode A.
La résistance de l'électrode est donc R = E/I= 19/0,2 = 95Ω.
