Conventions de signes pour tensions et courants
Afin de faciliter l'étude des chapitres qui suivront, nous présentons ici une notation permettant de donner systématiquement la polarité des tensions et le sens des courants.
Cas des distances
Nous allons tout d'abord appliquer cette notation conventionnelle au cas des distances afin de rendre la démonstration plus concrète.
Disons que la distance verticale entre deux points A et B est de 100 mètres.
Cette information seule n'indique pas si A est au-dessus ou au-dessous de B ; elle ne donne pas la position de A par rapport à B.
Il est possible de donner à la fois la distance et la position des points A et B en se servant de la convention simple des distances positives et négatives.
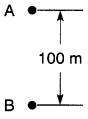
Ainsi, à la Fig. 7-1, puisque A est plus haut que B, on dira que la distance de A par rapport à B est de + 100 mètres.
Figure 7-1 Concept de distances positive (+) et négative (-). DAB = +100 m; DBA = -100 m

Inversement, B étant moins haut que A, on dira que la distance de B par rapport à A est de -100 mètres.
Pour simplifier davantage, on emploie la notation:
DAB = +100 mètres qui se lit: la distance de A par rapport à B = +100 mètres.
De la même façon, on aura:
DBA = -100 mètres qui se lit: la distance de B par rapport à A = -100 m
Addition de distances négatives et positives
En se référant à la Fig. 7-2, trouvons la distance verticale entre les points A et C, sachant que DAB = -3 m et que DBC = +5 m
Figure 7-2 Application des distances (+) et (-)
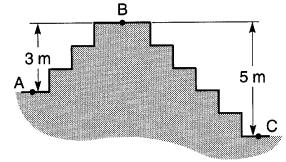
La distance DAC sera donnée par la somme algébrique DAB + DBC.
DAC = DAB + DBC = (-3 mètres) + (+5 mètres) = +2m
Il s'ensuit que A est 2 mètres plus haut que C. Le schéma de la Fig. 7-2 illustre bien ce problème.
On sait que B est plus haut que A de 3 mètres et que C est plus bas que B de 5 mètres (car la distance D CB est négative).
La personne qui partirait de A pour se rendre en C monterait de 3 mètres mais descendrait de 5 mètres. En C, il serait donc 2 mètres plus bas qu'en A (DCA= -2 mètres).
Méthode des deux indices
On se sert des mêmes conventions de signes pour les tensions électriques.
La Fig. 7-3 représente un générateur dont la borne A est (+) et la borne B est (-).
Figure 7-3 La polarité de la borne A est définie seulement par rapport à la borne B
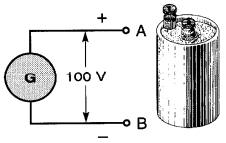
Il est à remarquer ici que la polarité de A est positive seulement par rapport à B; la borne A a une polarité en vertu de l'existence de B, car, en soi, elle n'a aucune polarité.
En d'autres termes, la borne A du générateur n'est pas positive par rapport à une des bornes d'une pile quelconque qui ne lui est pas raccordée (Fig. 7-3).
On dira de la même façon que la borne B est négative par rapport à la borne A.
Comme pour les distances, la notation suivante est employée:
EAB = +100 V (qui se lit : tension de A par rapport à B) EBA = -100V (qui se lit : tension de B par rapport à A)
Par exemple, si l'on sait que la génératrice de la Fig. 7-4 a une tension E21 = -300 V, il s'ensuit que la tension entre ses bornes 1 et 2 est de 300V et que la borne 2 est négative par rapport à la borne 1.
Figure 7-4 E21 = -300 signifie que la polarité de 2 est négative par rapport à la borne 1
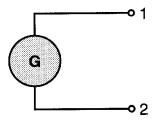
Cela revient à dire que la borne 1 est positive par rapport à la borne 2. Cette notation s'appelle méthode des deux indices.
Graphique d'une tension alternative Au chapitre 22 nous étudierons des sources de tension dont la polarité des bornes alterne périodiquement.
Ces tensions alternatives peuvent être avantageusement représentées au moyen d'un graphique. On porte sur un axe vertical la valeur de la tension à chaque instant, et, sur un axe horizontal, la valeur correspondante du temps en secondes.
Les valeurs de tension sont positives quand elles sont au-dessus de l'axe horizontal, et négatives lorsqu'elles sont en dessous (voir Fig. 7-5).
Figure 7-5 Représentation graphique d'une tension alternative
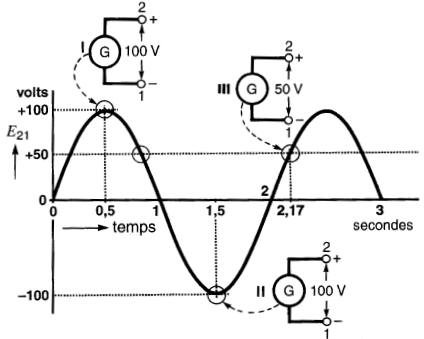
Par exemple, à partir de l'instant zéro, la tension E21 de la génératrice croît d'une valeur nulle à + 100 volts pour redevenir nulle au bout d'une seconde. Pendant cet intervalle, la borne 2 est positive par rapport à la borne 1.
Pendant l'intervalle de 1 à 2 secondes, E21 est négative, donc la borne 2 est négative par rapport à la borne 1. Les conditions qui existent après 0,5, 1,5 et 2,17 secondes sont clairement illustrées par les schémas I, II, III de la Fig. 7-5.
Addition de tensions positives et négatives
Les deux exemples suivants donnent la méthode à suivre pour déterminer la somme de plusieurs tensions.
Exemple 7-1
Soient deux génératrices G 1 et G2 dont les tensions respectives sont données à la Fig. 7-6.
Figure 7-6 Voir exemple 7-1
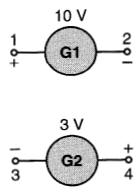
Elles peuvent être groupées en série de deux façons :
a) la borne 2 de G 1 raccordée i1 la borne 3 de G2 (Fig. 7-7)
b) la borne 2 de G I raccordée à la borne 4 (le G3 Fi. 7-8)
Trouver la tension résultante dans les deux cas.
Solution
a) La borne 2 est raccordée à la borne 3, et on cherche la tension E1-4.
En se référant à la Fig. 7-7, la tension
E1-4 est donnée par:
E1-4 = E1-2 + E3-4
D'après la Fig. 7-6:
E1-2 =+10V et E3-4 =-3V
il s'ensuit que:
E1-4 =(+10)+(-3)=+7V
La tension entre les bornes 1 et 4 est de 7 volts, et la borne 1 est positive par rapport à la borne 4.
Figure 7-7 E14 = +7 V (voir exemple 7-1)
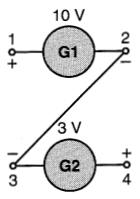
b) La borne 2 est reliée à la borne 4, et on cherche la tension E13.
En se référant à la Fig. 7-8, la tension E1-3 est égale à la somme E1-2 + E4-3 (et non pas E1-2 + E3-4, car la borne 2 est reliée à la borne 4 et non à la borne 3).
Or, d'après la Fig. 7-6, E1-2 = + 10 V et E4-3 = +3 V,
donc E1-3 = E1-2 + E4-3
E1-3 = (+ 10) + (+ 3) = + 13 V
La tension entre les bornes 1 et 3 est de 13 volts, et la borne 1 est positive par rapport à la borne 3.
b) La borne 2 est reliée à la borne 4, et on cherche la tension E1-3.
En se référant à la Fig. 7-8, la tension E1-3 est égale à la somme E1-2 + E4-3 (et non pas E1-2 + E3-4, car la borne 2 est reliée à la borne 4 et non à la borne 3).
Or, d'après la Fig. 7-6, E1-2 = + 10 V et E4-3 = +3 V, donc
E1-3 = E1-2 + E4-3
E1-3 = (+ 10) + (+ 3) = + 13 V
La tension entre les bornes 1 et 3 est de 13 volts, et la borne 1 est positive par rapport à la borne 3.
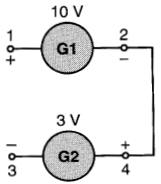
Figure 7-8 E13 = +13 V (voir exemple 7-1)
Exemple 7-2
Soit quatre génératrices indépendantes ayant les polarités indiquées à la Fig. 7-9.
Figure 7-9 Génératrices indépendantes (voir exemple 7-2)
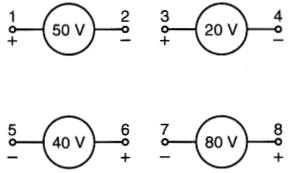
Déterminer la valeur et la polarité de la tension résultante (E l 8 ) lorsque les génératrices sont groupées en série (Fig. 7-10).
Solution
D'après les valeurs et polarités données à la Fig. 7-9 pour chacune des génératrices, le lecteur vérifiera que :
E1-2 = +50V donc E2-1 = -50V
E3-4 = +20V donc E4-3 = -20V
E5-6 = -40V donc E6-5 = +40V
E7-8 = -80V donc E8-7 = +80V
Sachant que la borne 2 est reliée à la borne 4, que 3 est reliée à 6, et 5 à 7 (Fig. 7-10), la tension E1-8 sera donnée par:
E1-8 = E1-2 + E4-3 + E6-5 + E7-8 = (+50) + (-20) + (+40) + (-80) = -10V
Figure 7-10 Génératrices en série (voir exemple 7-2)
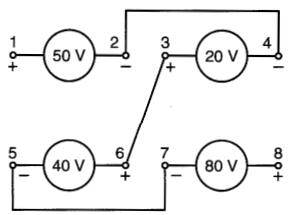
Cela signifie que la tension entre les bornes 1 et 8 est de 10 volts, et que la borne 1 est négative par rapport à la borne 8.
Exemple 7-3
Les deux machines à courant continu G 1 et G2 de la Fig. 7-11 alimentent une résistance R de 10Ω.
Figure 7-11 G1 est la source, G2 la charge
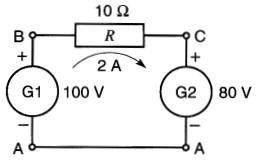
Les tensions à leurs bornes sont respectivement :
EAB =-100V et EAC = -80V
Déterminer la valeur et le sens du courant dans la résistance.
Solution
Pour trouver la valeur et le sens du courant dans la résistance, il faut tout d'abord trouver la valeur et la polarité de la tension EBC à ses bornes.
EBC= EBA + EAC = (+100) + (-80) = +20V
Cela signifie que B est positif par rapport à C, et inversement, que C est négatif par rapport à B. Le sens du courant dans la résistance sera donc de B vers C.
La tension aux bornes de la résistance étant de 20 V, l'intensité du courant sera 20 V/10Ω = 2A.
Les machines à courant continu sont réversibles, c'est-à-dire qu'elles peuvent fonctionner soit comme génératrices, soit comme moteurs. En connaissant le sens du courant dans le circuit, nous pourrons établir laquelle des deux machines agit comme génératrice.
En effet pour une source d'énergie électrique, le courant sort toujours de la borne positive.
Pour une charge, le courant entre par la borne positive.
En appliquant cette règle au circuit de la Fig. 7-11, on trouve que G1 agit comme source (génératrice) et que G2 agit comme charge (moteur).
puissance débitée par G1 = 2A x 100V = 200W
puissance reçue par G2 = 2A x 80V = 160W
puissance dissipée dans R = 2A x 2 V = 40W
La puissance absorbée par la résistance R est dissipée sous forme de chaleur tandis que la puissance électrique reçue par G2 (le moteur) est transformée en puissance mécanique.
Exemple 7-4
Dans l'exemple 7-3 , si nous augmentons la tension de la machine G2 à une valeur de 120 V tout en gardant la même polarité (Fig. 7-12), nous constatons que la valeur et le sens du courant changent.
En effet :
EBC = EBA + EAC = (+ 100) + (-120) = -20 V
Figure 7-12 G2 est la source
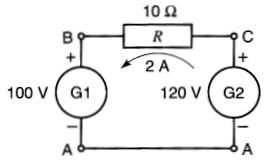
Solution La borne B est devenue négative par rapport à la borne C. Le courant dans le circuit de la Fig. 7-12 sera donc de sens inverse à celui de la Fig. 7-11.
Le courant aura la même valeur : I = 20 V/10 £2 = 2 A.
La machine G2 agira maintenant comme source (génératrice) et G1, comme charge (moteur).
Si les deux tensions EAB et EAC étaient égales, le courant deviendrait nul. On dirait alors que les machines «flottent» sur la ligne.
Courants positifs et courants négatifs
On se sert des signes (+) et (-) pour indiquer le sens du courant dans un circuit par rapport à un sens de référence représenté sur un schéma.
Le courant dans un élément de circuit comme une résistance (Fig. 7-13) peut circuler de A vers B ou de B vers A. Il peut circuler dans deux sens, l'un choisi comme positif (+), et l'autre comme négatif (-).
Figure 7-13 Le courant dans une résistance peut circuler de A vers B ou de B vers A.

Le sens positif du courant dans l'élément est indiqué arbitrairement au moyen d'une flèche (Fig. 7-14).
Figure 7-14 La flèche indique le sens (+) du courant.

Ainsi, si un courant de 2 ampères circule véritablement de A vers B dans cette figure, il circule dans le sens de la flèche (positif) et sera désigné par le nombre algébrique +2A.
Inversement, si le courant circule de B vers A (sens opposé à celui de la flèche), il sera désigné par le nombre -2A.
Exemple 7-5
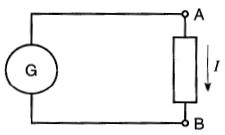
Le courant dans le circuit (Fig. 7-15) est de -8A.
Dans quel sens circule-t-il réellement, et quelle est la polarité des bornes A et B ?
Figure 7-15 Schéma montrant le sens arbitraire du courant I.
Solution
Puisque le courant est négatif, il circule dans le sens contraire à celui de la flèche, soit de B vers A dans la résistance.
Le courant dans une résistance circule toujours de la borne (+) à la borne (-) ; il s'ensuit que EBA a une valeur positive.
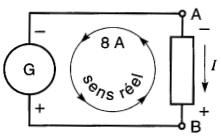
Notons que dans la génératrice le courant circule de A vers B (Fig. 7-16).
Figure 7-16 Sens réel du courant lorsque I = -8A
Exemple 7-6
La variation du courant dans une résistance R est donnée par le graphique de la Fig. 7-17.
Interpréter ce graphique.
Figure 7-17 Représentation graphique de la valeur et du sens d'un courant
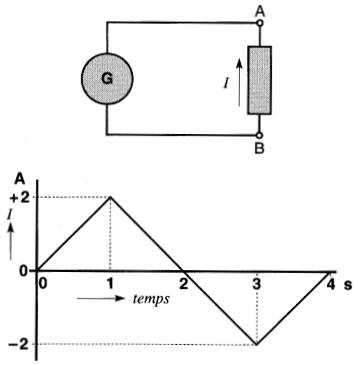
Solution Pendant l'intervalle de temps de 0 à 1 seconde, le courant croît de zéro à +2A.
Comme il est positif (d'après le graphique) il circule de B à A dans la résistance (sens de la flèche).
Pendant l'intervalle de 1 à 2 secondes, le courant décroît de + 2 A à zéro, mais il circule encore de B vers A dans la résistance.
Entre la deuxième et la troisième seconde, le courant croît de zéro à -2A, mais puisqu'il est négatif, il circule dans le sens contraire à celui de la flèche, soit de A vers B dans la résistance.
Cet exemple illustre qu'il est possible de représenter la valeur et le sens d'un courant variable dans un circuit en se servant d'un graphique et de la convention de signes.
Méthode des polarités
Bien qu'on puisse représenter la valeur et la polarité des tensions par la méthode des deux indices (E12, Eab, ECD, etc.,) on utilise souvent une autre convention.
Elle consiste à identifier la tension par un symbole quelconque (EI, EdV, etc.) et à identifier une des bornes par le signe (+).
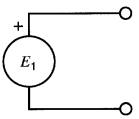
Par exemple, la Fig. 7-18 montre une tension EI dont une des bornes est arbitrairement marquée (+).
Il est entendu que l'autre borne est alors négative. (Dans plusieurs publications, pour éviter toute ambigüité, la borne négative est aussi indiquée).
Figure 7-18 Autre convention pour désigner la polarité d'une tension
Avec cette nouvelle convention, on applique les règles suivantes:
1. Si l'on sait que EI = +10V, cela signifie que la polarité réelle des bornes correspond bien à celle indiquée sur le schéma.
2. Inversement, si l'on sait que Et = -10V, la polarité réelle des bornes est l'inverse de celle indiquée sur le schéma.
Cette façon se désigner une tension s'appelle méthode des polarités.
Exemple 7-7
Soit le circuit de la Fig. 7-19 où, selon la convention établie plus haut, chacune des sources V1, V2, V3 possède une borne désignée arbitrairement d'un signe (+).
Figure 7-19 Polarités arbitraires de chacune des trois sources
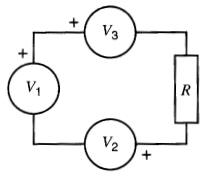
Indiquer la valeur et la polarité réelle de la tension aux bornes de chaque source sachant que
V1 = -4V, V2 = +10V et V3 = -40V
Solution
Les valeurs et les polarités réelles sont données à la Fig. 7-20.
Figure 7-20 Polarités réelles de chacune des trois sources
Le point A est (+) par rapport au point C, mais il est négatif par rapport au point B
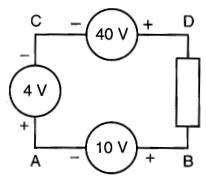
À première vue, il semble impossible que le point A soit à la fois positif (+) et négatif (-), mais rappelons-nous que le point A ne possède pas une polarité (+) et (-) en soi, mais par rapport aux points B et C respectivement.
En effet, le point A est négatif par rapport au point B et positif par rapport au point C, c'est pourquoi il porte deux signes contraires.
Cette nouvelle façon d'indiquer la polarité d'une tension nous sera particulièrement utile dans la section Solutions des circuits à courant continu, où nous traiterons de la solution des circuits plus complexes.
Taux de variation d'une tension
Lors de l'étude des circuits à courant alternatif, nous verrons que le taux de variation d'une tension ou d'un courant peut être tout aussi important que sa valeur et sa polarité instantanées.
Soit une tension E qui varie suivant la courbe de la Fig. 7-21.
Figure 7-21 Taux de variation d'une tension
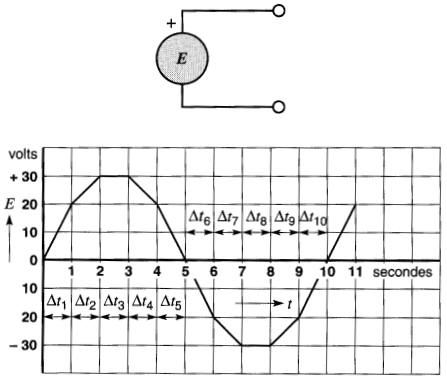
On constate que la tension augmente de 20 volts durant le premier intervalle Δt1 (de 0 à 1 seconde) et de 10 volts durant le deuxième intervalle Δt2 (de 1 à 2 secondes).
Pendant le troisième intervalle Δt3 (de 2 à 3 secondes), la tension ne varie pas.
On dit que le taux de variation est respectivement de 20 V/s, 10 V/s et 0 V/s durant les intervalles Δt1, Δt2 et Δt3. On observe que le taux est plus élevé quand la pente de la courbe est plus raide.
Lorsque la pente est horizontale (intervalle Δt3), le taux de variation est nul.
De plus, on note que pendant les intervalles Δt2 et Δt3, la pente de la courbe «monte» vers la droite de cette façon : / ; une telle pente, ou taux de variation, est considérée comme positive.
Passé le sommet de la courbe, on constate que le taux de variation pendant l'intervalle Δt4 est de nouveau 10 V/s et que pendant l'intervalle Δt5, il est de 20 V/s.
Cependant, la pente «descend» vers la droite de cette façon: \ ; on la considère comme négative. La pente est toujours négative pendant les intervalles Δt6 et Δt7 , devenant nulle pendant l'intervalle Δt8.
Durant les intervalles Δt9 et Δt10, la pente est de nouveau positive, indiquant un taux de variation positif. Il est clair que le taux de variation d'une tension est indépendant de sa valeur et de sa polarité instantanées.
Par exemple, lorsque la tension passe par zéro à l'instant t = 5s, son taux de variation est encore -20 V/s.
Aussi curieux que cela puisse paraître, une tension nulle peut posséder un taux de variation non nul.
Exemple 7-8
Déterminer le signe du taux de variation (+) ou (-) de la tension El de la Fig. 7-22 aux instants ta, tb, tc et td et indiquer les moments où ce taux de variation est nul.
Figure 7-22 Voir exemple 7-8
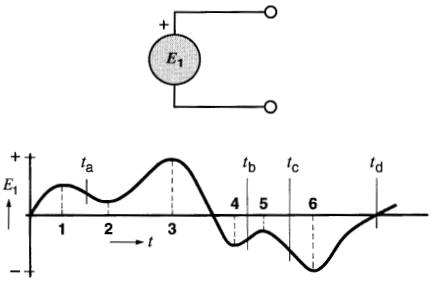
Solution
Les signes de taux de variation aux instants ta, tb, t, et td sont respectivement (-), (+), (-) et (+).
Le taux de variation est nul à chaque instant où la pente de la courbe est nulle, c'est-à-dire lorsqu'elle est horizontale. Cette condition se produit aux instants 1, 2, 3, 4, 5 et 6, 7, 9
Expression du taux de variation Le taux de variation d'une grandeur Q est donné par l'expression
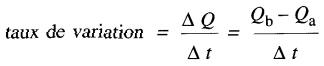 (7-1)
(7-1)
où ΔQ = variation de la grandeur Q
Δt = durée de la variation, en secondes
Qb = valeur de la grandeur Q à la fin de l'intervalle de temps
Qa = valeur de la grandeur Q au début de l'intervalle de temps
La grandeur Q peut être une tension, un courant, une puissance, un flux magnétique, etc.
On se souvient que le taux de variation est positif lorsque la courbe représentant la grandeur Q monte vers la droite et négatif lorsqu'elle descend vers la droite. Il est facile de trouver le taux de variation quand on connaît cette courbe en fonction du temps.
Figure 7-23 Calcul du taux de variation d'une grandeur Q à divers instants.
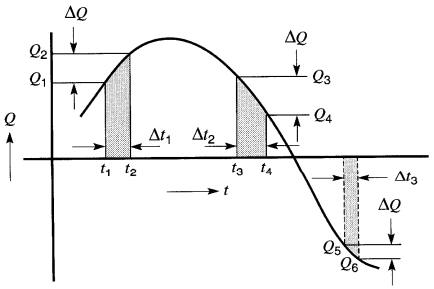
En se référant à la Fig. 7-23, le taux de variation pendant l'intervalle Δt1 est:
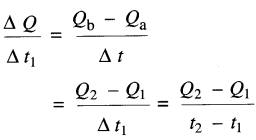
Durant l'intervalle Δt2, le taux de variation est :
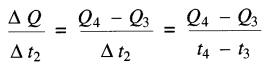
et durant l'intervalle Δt3, le taux de variation est:
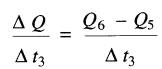
Niveau de potentiel
L'étude de cette section n'est nécessaire que pour comprendre la section Électronique de puissance.
Nous venons de décrire deux méthodes pour représenter les tensions dans un circuit. Nous présentons maintenant une troisième méthode qui nous sera particulièrement utile lors de l'analyse des circuits rencontrés en électronique de puissance. Il s'agit de la méthode des niveaux de potentiel.
Pour comprendre le fonctionnement des circuits électroniques, il est utile d'imaginer que les diverses bornes occupent un «niveau de potentiel» par rapport à une borne de référence.
La borne de référence est tout simplement un point convenable, choisi dans le circuit, que l'on affecte d'un potentiel électrique nul. Les niveaux de potentiel de tous les autres points du circuit sont alors mesurés par rapport à cette borne de référence. Le niveau de référence se représente par une ligne droite horizontale dont le potentiel électrique correspond à 0 V.
Considérons, par exemple, le montage de la Fig. 7-24 comprenant une batterie de 80 V, raccordée en série avec une source de tension alternative E31 ayant une tension crête de 100 V.
Figure 7-24 Choix d'un point de référence (1) pour établir le niveau de potentiel des autres points dans un circuit
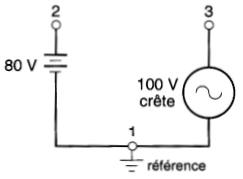
Parmi les trois bornes 1, 2 et 3, choisissons la borne 1 comme point de référence. Le niveau de potentiel de cette borne est alors représenté par la ligne horizontale 1 sur la Fig. 7-25.
Figure 7-25 Graphique montrant les niveaux des points 1, 2 et 3 lorsque le point 1 est choisi comme point de référence
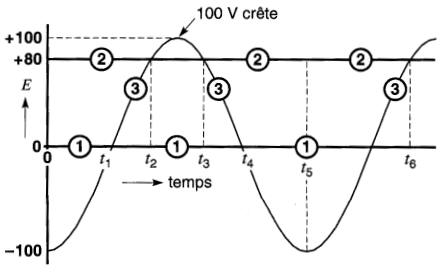
Considérons maintenant le niveau de potentiel de la borne 2.
À cause de la batterie, la différence de potentiel entre les bornes 1 et 2 est fixe à 80 V et la borne 2 est positive par rapport à la borne 1. On représente alors le niveau de cette borne par une deuxième ligne horizontale 2 située 80 V au-dessus de la ligne 1.
Intéressons-nous maintenant à la borne 3.
La tension E31 entre les points 1 et 3 est alternative et on supposera qu'au départ sa valeur est de 100V (valeur crête) et que la borne 3 est négative par rapport à la borne 1.
C'est dire qu'à t = 0, E31 = -100V.
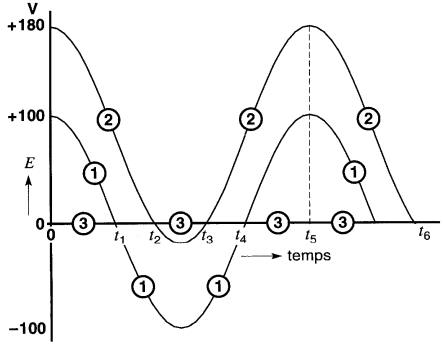
La tension étant alternative, le potentiel de la borne 3 devient tantôt positif, tantôt négatif par rapport à la borne 1, comme l'indique la courbe 3.
Ainsi, pendant l'intervalle 0 à t1, le niveau du point 3 est situé au-dessous du niveau de 1, ce qui indique que la borne 3 est négative par rapport à la borne 1.
Pendant l'intervalle t1 à t4, la polarité de E31 est inversée; par conséquent, le niveau de la borne 3 se trouve au-dessus de la ligne 1.
La borne 1 est alors négative par rapport à la borne 3 car la ligne 1 est au-dessous de la courbe 3.
Ces explications simples n'ajoutent rien à ce que l'on savait déjà, mais nous verrons que cette méthode des niveaux de potentiel permet d'identifier immédiatement la tension instantanée entre deux bornes quelconques d'un circuit, ainsi que leurs polarités relatives.
Par exemple, durant la période t2 à t3, la borne 3 est positive par rapport à la borne 2 car la courbe 3 est au-dessus de la ligne 2.
La tension entre ces deux bornes passe par un maximum de (100V - 80V) = 20V pendant cet intervalle.
Ensuite, de t3 à t6, la borne 3 est négative par rapport à la borne 2 et la tension E23 atteint une valeur maximale de + 180 V à l'instant t5. On aurait pu choisir une autre borne comme borne de référence.
Ainsi, dans la Fig. 7-26, nous avons choisi la borne 3 et, comme auparavant, on représente le potentiel nul de cette borne par une ligne horizontale (Fig. 7-27).
Figure 7-26 Le point 3 est choisi comme référence
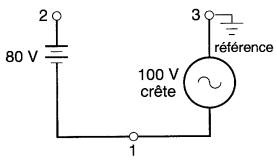
Figure 7-27 Graphique montrant les niveaux des points 1, 2 et 3 lorsque le point 3 est choisi comme point de référence
Sachant que la tension E31 est alternative et qu'au départ la borne 1 est positive par rapport à la borne 3 (Fig. 7-25), on peut tracer la courbe 1.
Pour déterminer le niveau de la borne 2, on sait qu'elle est toujours positive par rapport à la borne 1, la différence de potentiel restant constante et égale à 80 V.
Par conséquent, on trace la courbe 2 de sorte qu'elle soit toujours située 80 V au-dessus de la courbe 1.
Si l'on compare les Fig. 7-25 et 7-27, on constate qu'elles n'ont pas la même allure ; cependant à chaque instant, les polarités relatives et les différences de potentiel sont identiques.
Du point de vue électrique, les deux figures sont identiques et on laisse au lecteur le soin d'en faire la vérification.
Dans un montage électronique on sélectionne la borne de référence de sorte que le fonctionnement du circuit soit facile à suivre.
Résumé
Dans cette section nous avons vu les conventions que nous utiliserons dans ce manuel pour donner systématiquement la polarité des tensions et le sens des courants. Ces notations sont couramment utilisées dans l'industrie.
Pour les tensions, il existe 2 notations :
1) la méthode des deux indices et 2) la méthode des polarités.
Résumons ces 2 méthodes avec un exemple:
Soit une tension de 100 V entre les bornes A et B, A étant positive par rapport à B.
Avec la méthode des deux indices on écrira:
EAB= +100V ou EBA= -100V
Avec la méthode des polarités, on doit spécifier chaque tension sur le schéma par un symbole (disons E1) et ajouter un signe + vis-à-vis de la borne que l'on choisit arbitrairement.
Avec ces deux méthodes, on spécifie toujours la valeur et le signe de la tension entre 2 bornes quelconques.
On utilise parfois une troisième notation ou méthode du niveau de potentiel. Avec cette méthode, toutes les tensions sont mesurées par rapport à une borne commune ou borne de référence.
Pour la notation des courants, on spécifie sur le schéma chaque courant à l'aide d'une flèche et d'un symbole (ex. : I, IA).
La flèche indique le sens du courant choisi arbitrairement positif.
Enfin, nous avons expliqué le concept de taux de variation d'une grandeur.
Par exemple, un taux de variation ΔI/Δt = + 10 A/s pour un courant I indique que ce courant augmente à cet instant, même si la valeur du courant est négative.
PROBLÈMES
Niveau pratique
7-1 Trois sources à courant continu, G1, G2, G3 génèrent des tensions E12 = + 100V, E34 = + 40V et E56 = -60V.
Indiquer les polarités (+) (-) des bornes dans chaque cas (Fig. 7-28).
Figure 7-28 Voir problème 7-1

7-2 Dans le problème 7-1, si Gl et G2 sont reliées en série, quelle est la tension entre les bornes libres si:
a) les bornes 2 et 4 sont reliées ensemble
b) les bornes 1 et 4 sont reliées ensemble
7-3 Dans le problème 7-1, si les trois sources sont connectées en série, quelle est la tension et la polarité entre les bornes libres si :
a) les bornes 2-3 et 4-5 sont reliées ensemble
b) les bornes 1-4 et 3-6 sont reliées ensemble
c) les bornes 1-3 et 4-6 sont reliées ensemble
d) les bornes 1-6 et 5-3 sont reliées ensemble
e) les bornes 2-6 et 5-3 sont reliées ensemble
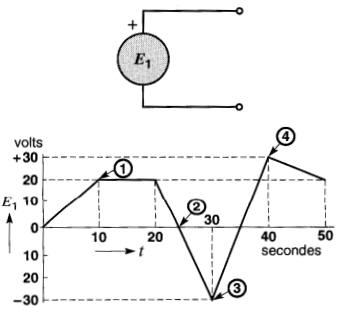
7-4 En se reportant à la courbe de variation de la tension El en fonction du temps (Fig. 7-29), indiquer sur le schéma de la génératrice la valeur de sa tension et la polarité de ses bornes aux instants (1), (2), (3) et (4).
Figure 7-29 Voir problème 7-4
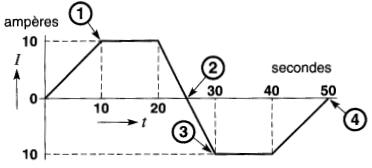
7-5 Dans le circuit de la Fig. 7-30, quels sont les valeur et le sens réel du courant, aux instants (1), (2), (3) et (4)?
Quelle est la polarité de la borne a par rapport à la borne b à chaque instant?
Figure 7-30 Voir problème 7-5
7-6 En se reportant de nouveau à la Fig. 7-29, donner le taux de variation de la tension pendant chaque intervalle de temps de 10 secondes et indiquer son signe.
7-7 En se reportant à la Fig. 7-30, donner le taux de variation du courant pendant chaque intervalle de temps de 10 secondes et indiquer son signe.
7-8 Dans la Fig. 21-11 (section Capacitance),
quel est le taux de variation moyen de la tension pendant les intervalles suivants :
a)0 à 7s b)7s à 14s c)14s à 21s
7-9 Dans la Fig. 21-12 ,
quel est le taux de variation moyen de la tension pendant les intervalles suivants :
a)28s à 35s b)20 s à 22s c) 20,99 s à 21,01 s
7-10 Dans la Fig. 21-17, quel est le taux de variation de la tension aux instants suivants :
a)5s b)8s c)11s
7-11 Dans la Fig. 7-5, quel est approximativement le taux de variation de la tension aux instants suivants :
a) 0,5 s
b) 1 s
c) 2,17 s
Réponses
2a) E13 = + 60V; 2b) E23 = -140V;
3a) E16 = + 80V; 3b) E25 = -80V; 3c) E25 = 0V; 3d) E24 = 0V; 3e) E14 = + 200V;
4)+20V;0V;-30V;+30V;
5)+10A;0A; -10A;0A;
6) + 2 V/s; 0 V/s; -5 V/s; + 6 V/s; -1 V/s;
7) +1 A/s; 0 A/s; -2 A/s; 0 A/s, +1 A/s;
8a) - 9,14 V/s; 8b) -4,57 V/s; 8c) -2,28 V/s;
9a) +0,57 V/s; 9b) +1,7 V/s; 9c) +1,7 V/s;
10a) +5 V/s; 10b) -30 V/s; 10c) +10 V/s;
11a) 0 V/s; 11b) -314 V/s; 11c) +272 V/s
