Courants électriques et champs magnétiques

Électrotechnique

PRINCIPE I DE L'ÉLECTROMAGNÉTISME

L'électromagnétisme est l'étude des phénomènes résultant de l'interaction des courants électriques et des champs magnétiques.

Principes de l'électromagnétisme Dans ce livre, nous avons divisé arbitrairement l'électromagnétisme en quatre principes fondamentaux comme suit.

PRINCIPE I Création d'un champ magnétique par un courant (cette section)

PRINCIPE II Force exercée sur un courant placé magnétique (section Forces électromagnétiques)

PRINCIPE III Déplacement d'un conducteur dans un champ magnétique, induction d'une tension
(section Tension induite dans un conducteur)

PRINCIPE IV Variation du champ magnétique à l'intérieur d'une boucle, induction d'une tension
(section Induction électromagnétique)

Dans les manuels de physique, les principes I et II sont présentés respectivement sous les noms de loi d'Ampère et loi de Lorenz, tandis que les principes III et IV sont deux expressions de la loi de l'induction électromagnétique de Faraday.

Le fonctionnement des machines électriques, des relais, des transformateurs et, plus généralement, de tout dispositif électromagnétique, est basé sur un ou plusieurs de ces quatre principes.

Champ magnétique créé par un courant

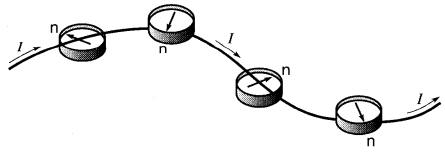
Si l'on déplace une boussole le long d'un fil parcouru par un courant, on observe que l'aiguille s'oriente toujours perpendiculairement à celui-ci, même aux endroits où le fil est courbé. Lorsqu'on change le sens du courant, l'aiguille s'oriente de nouveau suivant une direction perpendiculaire au fil mais en sens inverse.

On constate également que l'aiguille change de sens suivant que la boussole est placée au-dessus ou en dessous du fil
(Fig. 13-1).

Figure 13-1 Un courant électrique produit un champ magnétique

Enfin, lorsque le courant cesse, l'aiguille reprend son orientation normale dans la direction du champ magnétique terrestre.

Ce phénomène, remarqué pour la première fois en 1819 par le physicien Hans Christian Oersted, est une des plus importantes découvertes du siècle dernier.

Oersied a trouvé qu'un conducteur parcouru par un courant s'entoure d'un champ magnétique analogue à celui produit par un aimant. Ce fut la première d'une série de découvertes remarquables dont le sommet fut la découverte de l'induction électromagnétique par Faraday.

Forme et sens du champ

Soit un conducteur raccordé à une pile de sorte qu'il porte un courant I (Fig. 13-2).

Figure 13-2 Les lignes de force autour d'un conducteur forment des cercles fermés. La nature de ce champ magnétique est révélée par la limaille de fer

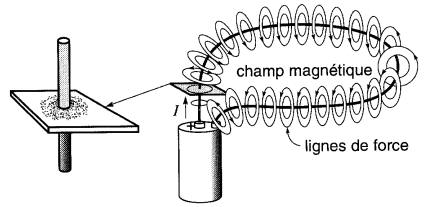
Une partie du conducteur traverse une feuille de carton que l'on saupoudre de limaille de fer. On remarque que la limaille se dispose autour du conducteur en une série de cercles concentriques qui révèlent la présence de lignes de force.

Ce champ circulaire entoure le fil sur toute sa longueur, et les lignes de force forment des cercles dont le plan est toujours perpendiculaire à la direction du conducteur.

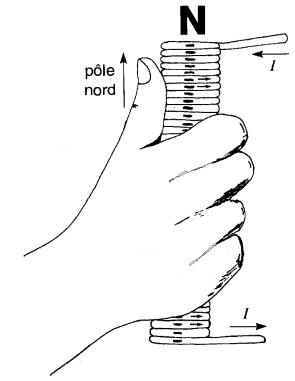
On peut déterminer le sens des lignes de force à l'aide d'une boussole, mais il est plus simple de retenir la règle illustrée à la Fig. 13-3, appelée règle de la main droite:

Figure 13-3 La règle de la main droite permet de déterminer le sens des lignes de force, connaissant le sens du courant I. L'entrée du courant dans le conducteur est indiqué par une croix; la sortie par un point

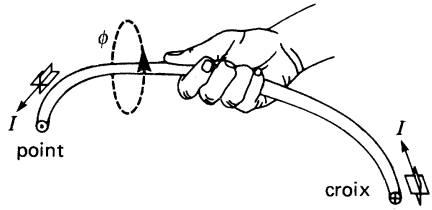
Règle de la main droite

Si l'on tient le conducteur dans la main droite, le pouce étant orienté dans le sens du courant, les doigts pointeront dans le sens du flux.

Inversement, si l'on connaît le sens du flux, on peut, à l'aide de la même règle, déduire le sens du courant qui le produit.

Convention

Il est d'usage de représenter le sens du courant à l'extrémité d'un conducteur au moyen d'une croix pour un courant pénétrant dans le conducteur (empennage d'une flèche) et d'un point pour un courant sortant du conducteur (pointe d'une flèche) (Fig. 13-3).

On ne doit pas confondre la croix avec le signe (+).

Densité de flux

Lorsqu'un conducteur porte un courant, les lignes de force qui entourent le conducteur deviennent de plus en plus espacées à mesure qu'on s'éloigne du conducteur (Fig. 13-4). En effet, le nombre de lignes de force par mètre carré diminue. Le flux magnétique est donc moins dense au point B qu'au point A.

Figure 13-4 La densité de flux décroît à mesure qu'on s'éloigne du conducteur.

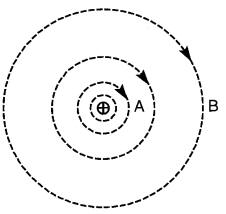
Le champ existe tout autour du conducteur, même aux endroits très éloignés.

Cependant, à quelques centimètres d'un conducteur parcouru par un courant, le champ devient si faible qu'il réussit à peine à faire dévier l'aiguille d'une boussole.

Comme ordre de grandeur, signalons qu'un courant de 10 ampères produit à 4 cm du centre d'un conducteur une densité de flux de 50 µT, soit environ celle du champ terrestre.

La densité de flux à un point donné est proportionnelle au courant qui traverse le conducteur: si le courant double, la densité de flux double. Cette densité de flux est indépendante du diamètre du conducteur et de la nature de celui-ci.

Ainsi, des conducteurs de cuivre et de fer, de diamètres différents mais portant le même courant, produisent, dans l'air, des champs de même densité à 10 cm de leur centre (Fig. 13-5).

Figure 13-5 La densité de flux B1 = densité de flux B2.

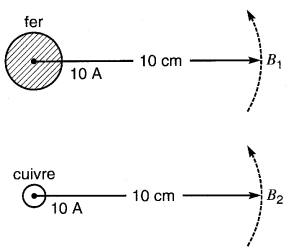
On peut calculer la valeur de la densité de flux autour d'un conducteur rectiligne par la formule :

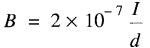
où

B = densité de flux, en teslas [T]

I = courant, en ampères [A]

d = distance, en mètres [m]

2 x 10^-7 = constante tenant compte des unités

Exemple 13-1

Calculer la valeur de la densité de flux à une distance de 2 cm d'un fil AWG #11 qui porte un courant de 10 A.

Quelle est la valeur de la densité de flux à la surface du fil?

Solution

La densité de flux à une distance de 2 cm vaut:

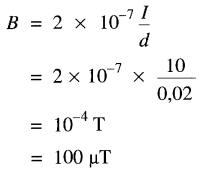
Le fil #11 possède un diamètre de 2,3 mm, soit un rayon de 1,15 mm. À la surface du conducteur, la densité de flux est donc:

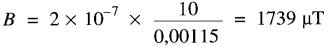
Champ créé par plusieurs conducteurs Le champ magnétique autour de plusieurs conducteurs est égal à la somme des champs créés par chacun d'eux.

Ainsi, un faisceau de 100 conducteurs portant chacun un courant de 5 ampères produit le même champ qu'un seul conducteur parcouru par un courant de 500 ampères (Fig. 13-6).

Figure 13-6 Champ magnétique créé par (a) est le même que celui créé par (b)

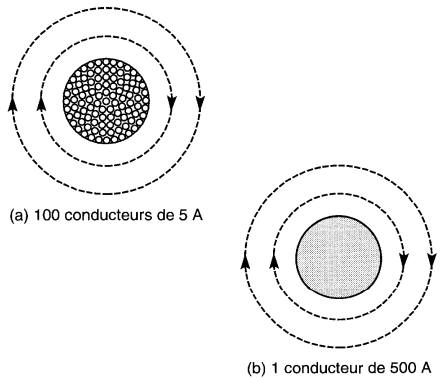
Cela permet de créer des champs intenses avec des courants relativement faibles.

Par ailleurs, deux conducteurs voisins, portant des courants égaux mais de sens contraires, produisent, ensemble, un champ négligeable à quelques millimètres de distance (Fig. 13-7).

Figure 13-7 Champ créé par deux courants égaux de sens contraires. Lorsque les conducteurs isolés se touchent, le champ résultant est faible

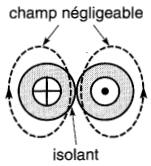
Les courants créent des champs de sens contraires de sorte que le champ résultant est faible, même pour des courants élevés.

En utilisant un câble coaxial formé d'un fil central entouré d'un conducteur de retour cylindrique (Fig. 13-8).

Figure 13-8 Un câble coaxial ne produit aucun champ extérieur

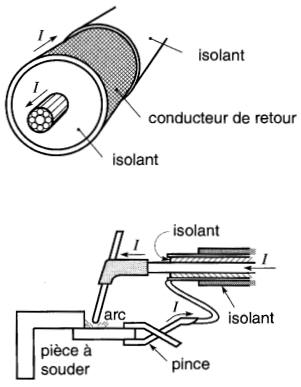
On peut éliminer complètement le champ à l'extérieur du câble; toutefois il existera un champ dans l'espace séparant les deux conducteurs. Ce montage est utilisé dans les câbles de soudure à l'arc afin de les empêcher de se coller contre des pièces de fer lorsqu'ils portent des courants intenses.

Les câbles coaxiaux trouvent aussi une application dans les circuits à haute fréquence, ce qui permet d'éviter les interférences électromagnétiques avec les circuits voisins.

Champ produit par un courant dans une spire

Soit un fil circulaire (spire) traversant une feuille de carton en deux points A et B.

Saupoudrons cette feuille de limaille de fer comme dans le cas du conducteur rectiligne. Lorsque le fil est parcouru par un courant, des lignes de force se dessinent comme sur la Fig. 13-9.

Figure 13-9 Champ magnétique créé par un courant circulant dans une spire

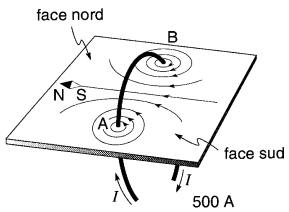
Aux points A et B, les lignes forment des courbes fermées; à mesure qu'on s'éloigne de ces deux points, les lignes suivent des courbes de moins en moins prononcées. Au centre, la ligne est rigoureusement droite.

Si l'on applique la règle de la main droite à cette spire, on trouve que le sens des lignes de force doit être le même que celui représenté sur la Fig. 13-9.

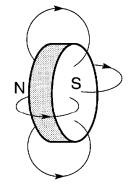
Par analogie avec les aimants, on appelle face nord (ou pôle nord) celle par laquelle sortent les lignes de force et face sud (ou pôle sud) celle par laquelle elles rentrent.

En effet, une spire parcourue par un courant produit un spectre magnétique semblable à celui produit par un aimant permanent en forme de disque (Fig. 13-10).

Figure 13-10 Le champ créé par un aimant permanent en forme de disque est le même que celui produit par le courant de la figure 13-9

Noter que si la spire de la Fig. 13-9 portait, par exemple, un courant de 500 ampères, elle produirait un champ identique à celui d'une bobine de même forme composée de 100 spires et portant un courant de 5 A (Fig. 13-11).

Figure 13-11 Le champ magnétique créé par cette bobine est le même que celui créé par la spire de la Fig. 13-9

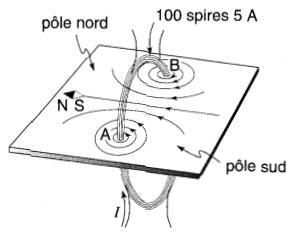
Force magnétomotrice (FMM)

Le produit du courant par le nombre de spires s'appelle force magnétomotrice d'une bobine.

Ainsi, une bobine de 50 spires portant un courant de 8 ampères, développe une force magnétomotrice (symbole FMM) de:

FMM = 50 spires x 8 ampères = 400 ampères

Une telle bobine crée le même effet magnétique qu'une seule spire portant un courant de 400 ampères.

L'unité SI de force magnétomotrice est l'ampère (A) ; il représente la différence de potentiel magnétique produit par un courant de 1 ampère circulant dans 1 spire.

Le terme «ampère-tour» utilisé autrefois équivaut à une FMM de 1 ampère. Nous continuerons à utiliser le terme «ampère-tour» (plutôt que simplement «ampère») aussi souvent que la clarté du texte l'exigera.

Champ d'un solénoïde (bobine longue)

On appelle solénoïde un fil enroulé régulièrement en hélice de façon à former une bobine longue (Fig. 13-12).

Figure 13-12 Champ magnétique créé par un solénoïde

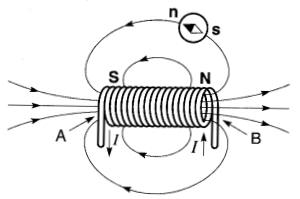
Une telle bobine parcourue par un courant produit le même champ qu'une série de spires indépendantes parcourues par le même courant. À l'intérieur de la bobine, les lignes de force sont parallèles à l'axe du solénoïde.

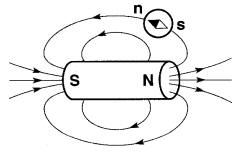
À l'extérieur, elles sont distribuées exactement comme celles d'un barreau aimanté (Fig. 13-13).

Figure 13-13 Ce barreau aimanté produit le même champ magnétique que le solénoïde de la Fig. 13-12

Comme pour le barreau aimanté, on appelle pôle nord l'extrémité de la bobine par laquelle sortent les lignes de force, et pôle sud l'extrémité par laquelle elles rentrent.

Si l'on applique la règle de la main droite au courant qui circule dans une spire du solénoïde de la Fig. 13-12, on constate que les lignes de force doivent rentrer par l'extrémité A du solénoïde; celle-ci constitue donc le pôle sud. Pour changer le sens du champ, il suffit de changer le sens du courant.

On peut remplacer un barreau aimanté par un solénoïde car, leurs spectres magnétiques étant semblables, ils jouissent tous deux des mêmes propriétés magnétiques.

En effet, on vérifie expérimentalement que si l'on approche un aimant permanent du solénoïde parcouru par un courant, il y a attraction ou répulsion, comme dans le cas de deux aimants permanents.

Le flux créé par un solénoïde, dans l'air ou dans le vide est proportionnel au courant qui circule dans celui-ci : si l'on double le courant, le flux double.

Le nombre de lignes de force dépend donc de la FMM de la bobine. Le flux dépend aussi du diamètre et de la longueur du solénoïde; l'effet de ces facteurs sera étudié dans le chapitre suivant.

Règle de la main droite pour un solénoïde

Bien que l'on puisse trouver le pôle nord d'un solénoïde en appliquant la méthode décrite dans la section ci-haut, il est plus facile d'employer la règle suivante.

Si l'on imagine qu'on tient la bobine de la main droite & façon que les doigts soient dirigés dans le sens du courant circulant dans les spires, le pouce pointera vers k pôle nord du solénoïde.

La Fig. 13-14 illustre l'application de cette règle.

Figure 13-14 Méthode simple pour trouver le pôle nord d'un solénoïde

Comparaison des champs produits par un aimant et un solénoïde à noyau d'air

Si l'on cherche à produire avec un solénoïde le même flux que celui créé par un aimant permanent de même grosseur, on s'aperçoit que la bobine doit développer une FMM énorme.

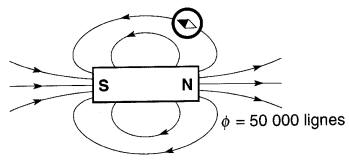
Par exemple, un aimant permanent en alnico V de 2,5 cm de diamètre et de 15 cm de long produit un flux de 50 000 lignes (500 µWb) environ Fig. 13-15.

Figure 13-15 Cet aimant permanent produit 50 000 lignes de force

Pour produire le même flux avec un solénoïde de mêmes dimensions, mais à noyau d'air, il faudrait que la bobine développe une FMM d'au moins 1 2_0 000 ampères (Fig. 13-16).

Figure 13-16 Cette spire, portant un courant de 120 000 A, produit le même champ magnétique que l'aimant de la Fig . 13-15

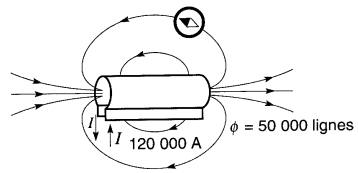
C'est dire que cette bobine devrait supporter un courant de 120 000 A si elle était formée d'une seule spire, ou de 120 A si elle en comportait 1000.

Dans un cas comme dans l'autre, la bobine brûlerait en quelques secondes à cause des fortes pertes par effet Joule. Il est impossible de produire une telle FMM avec une bobine ayant des dimensions aussi restreintes.

On en conclut qu'il n'est pas pratique de construire des solénoïdes à noyau d'air produisant des champs magnétiques aussi intenses que ceux obtenus avec les aimants permanents modernes.

Électro-aimants

Soit un solénoïde à noyau d'air produisant une FMM modérée de sorte que la bobine ne surchauffe pas. On produira ainsi un flux, mais à peine suffisant pour attirer un clou.

Mais si l'on introduit un noyau de fer doux à l'intérieur du solénoïde, on constate que le flux augmente de façon spectaculaire et peut devenir aussi grand que celui provenant d'un aimant permanent de mêmes dimensions.

Pourtant, la bobine ne développe qu'une FMM modeste. La combinaison d'un solénoïde et d'un noyau de fer doux nous ouvre des possibilités intéressantes.

Cette combinaison, appelée électro-aimant, nous permet non seulement de créer des champs aussi intenses que ceux produits par les aimants permanents, mais aussi de les faire varier à volonté (et même les inverser), en faisant simplement varier le courant circulant dans la bobine.

Comment expliquer ce phénomène?

Il faut avoir recours aux domaines magnétiques à l'intérieur du morceau de fer doux. Sous l'influence du faible champ produit par le solénoïde, les domaines s'orientent tous dans le même sens que celui-ci, ajoutant ainsi leur flux énorme à celui créé par le solénoïde seul.

L' orientation des domaines équivaut à orienter dans une même direction toutes les FMM atomiques créées par la rotation et le «spin» des électrons dans le fer.

Applications des électro-aimants

Les électro-aimants peuvent prendre diverses formes : cylindrique, en fer à cheval, cuirassée, à noyau plongeur, etc., suivant les applications.

En voici quelques exemples:

I. Pôles des génératrices et des moteurs

Les électro-aimants trouvent leur application la plus importante dans les génératrices et les moteurs. Ils servent à créer un champ magnétique très dense dans l'es.pace appelé entrefer (Fig. 13-17).

Figure 13-17 Pôles d'une génératrice à courant continu

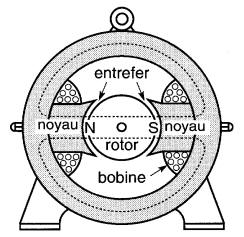
Pour les machines à courant continu, les bobines sont enroulées autour de chacun des noyaux de façon à for.mer un pôle nord et un pôle sud. Les lignes de force circulent de la façon indiquée sur la figure .

Il. Électro-plongeur

L'ensemble d'une bobine excitatrice et d'un noyau de fer libre de se déplacer à l'intérieur de la bobine constitue un électro-plongeur (Fig. 13-18).

Figure 13-18 Principe de l'électro-plongeur

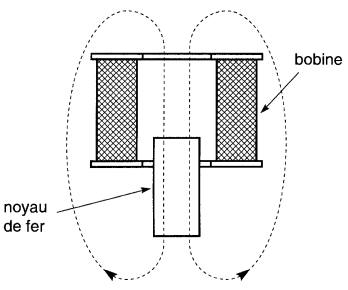
 Lorsque le courant circule dans la bobine, le noyau s'aimante par influence et est alors attiré contre la force de gravité vers le centre de la bobine où le champ est le plus dense. Ce mode de déplacement est mis à profit dans de nombreux disjoncteurs, contacteurs, freins magnétiques et relais.

a) Disjoncteurs électromagnétiques

Les disjoncteurs sont des appareils qui coupent automatiquement le circuit quand l'intensité du courant dépasse une certaine valeur (Fig. 13-19).

Figure 13-19 Électro-aimant servant à déclencher un disjoncteur

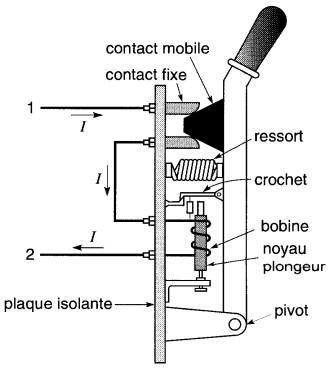
Grâce à la présence d'un crochet articulé, les contacts fixes d'un interrupteur sont court-circuités par un con.tact mobile, solidaire du bras mobile du disjoncteur.

Le courant I entre par la borne 1, passe par le contact fixe supérieur, le contact mobile, le contact fixe inférieur, à travers la bobine de l'électro-aimant à noyau plongeur, et ressort par la borne 2.

Lorsque le courant devient trop intense, le noyau plongeur est attiré vers le centre de la bobine et, en remontant. fait sauter le crochet. Le ressort comprimé se détend poussant le bras mobile vers la droite, ce qui coupe le circuit.

b) freins magnétiques

La Fig. 13-20 représente un frein d'ascenseur. Lors.que l'ascenseur est à l'arrêt, un ressort très puissant serre les deux sabots contre un tambour.

Figure 13-20 Électro-aimant servant à commander un frein

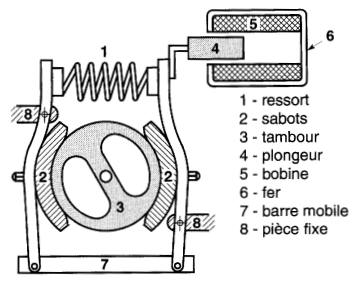
Dès que le courant circule dans la bobine, celle-ci attire brusquement le plongeur qui, en agissant contre la tension du ressort, libère le tambour.

Au moment où le courant est interrompu, le tambour est freiné à nouveau. La bobine de l'électro-aimant est cuirassée en fer afin de concentrer les lignes de force.

c) Relais à noyau mobile

La circulation du courant dans la bobine du relais (Fig. 13-21), provoque le déplacement du plongeur.

Figure 13-21 Électro-aimant servant à actionner les contacts d'un relais

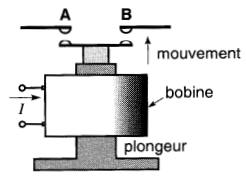
Le contact mobile, solidaire du plongeur, ferme le circuit entre les bornes A et B. Le relais est donc un interrupteur que l'on peut commander à distance en faisant circuler ou non le courant I dans la bobine.

III. Électro-aimant à noyau fixe

Contrairement à un électro-plongeur, il existe des électro-aimants dont le noyau est fixe.

En voici quelques exemples:

a) Électro-aimant droit

Lorsque le courant passe dans la bobine (Fig. 13-22), des pôles N, S apparaissent aux extrémités du noyau.

Figure 13-22 Électro-aimant à noyau fixe utilisé dans un relais

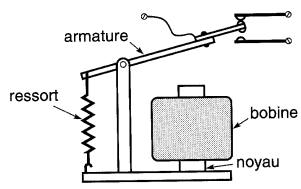
Une armature de fer doux, placée au-dessus du noyau, s'aimante par influence et est attirée vers le noyau. Lorsque le courant cesse dans la bobine, l'armature est ramenée par le ressort.

Ce déplacement d'un armature par un électro-aimant est à la base d'un grand nombre d'appareils:

sonnerie électrique, relais, appareils de commande à distance, etc.

b) Électro-aimant enfer à cheval

On préfère souvent à l'électro-aimant droit de la Fig. 13-22, l'électro-aimant en fer à cheval qui a l'avantage d'utiliser l'attraction des deux pôles (Fig. 13-23).

Figure 13-23 Électro-aimant à noyau fixe, où on utilise les deux pôles pour attirer une armature

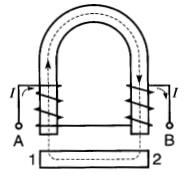
Les deux enroulements doivent être raccordés en série afin que les FMM produites par chaque bobine s'additionnent.

c) Sonnerie électrique L'organe principal d'une sonnerie électrique est un électro-aimant E en forme de fer à cheval (Fig . 13-24).

Figure 13-24 Électro-aimant à noyau fixe utilisé dans une sonnette

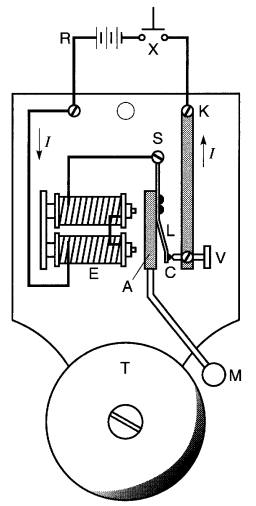
 Si on appuie sur le bouton poussoir X, le circuit électrique se ferme et le courant passe dans les bobines de l'électro-aimant E puis retourne à la pile par la lame flexible L et par la pointe de la vis fixe V qui fait con.tact au point C.

L'électro-aimant excité attire l'armature A et le marteau M vient frapper le timbre T.

Mais dès que cette attraction a lieu, le contact de la vis fixe et de la lame flexible se trouve rompu et le courant ne passe plus.

L' aimantation cesse et la lame ramène l'armature à son point de repos. Le courant est ainsi rétabli et l'attraction a lieu à nouveau, et ainsi de suite . Cette succession de chocs du marteau se produit très rapidement et aussi longtemps que l'on appuie sur le bouton X.

d) Électro-aimants spéciaux

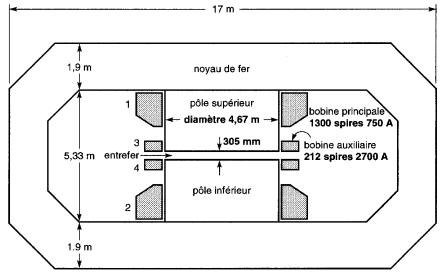
La Fig. 13-25 montre un électro-aimant énorme qui a servi à étudier les propriétés des particules électro.niques. Les détails techniques sont donnés au tableau 13-1.

Figure 13-25a Le synchro-cyclotron de Berkeley servait à accélérer les particules atomiques telles que les protons, les deutérons, etc. Il utilise le champ magnétique créé par un immense électro-aimant composé de deux bobines principales, de deux bobines auxiliaires et d'un noyau de fer.

La photo montre une partie du noyau de fer et les bobines blindées supérieures et inférieures. Les particules atomiques sont accélérées dans l'entrefer, caché dans cette photo par la chambre rectangulaire sous vide (gracieuseté de Lawrence Berkeley Laboratory -University of California).

Figure 13-25b Vue en coupe et dimensions de l'électro-aimant, à l'échelle . Cet accélérateur illustre bien la construction d'un électro.aimant puissant qui a servi à faire des découvertes atomiques importantes.

Calcul des bobines pour électro-aimants

Les notions simples que nous avons étudiées dans ce chapitre nous permettent déjà de faire certains calculs sur les électro-aimants.

En voici trois exemples:

Exemple 13-2

Soit une bobine avant 5000 spires et dont la résistance est de 200Ω. Quelle sera sa FMM si elle est raccordée à une source de 50V?

Quelle sera la puissance dissipée en chaleur?

Solution

Le courant tiré par la bobine sera:

I = E/R = 50 / 200 = 0,25A

La FMM = courant x tours = 0,25 x 5000 = 1250 ampères-tours = 1250A

La puissance dissipée en chaleur est donnée par :

P = EI = 50 X 0,25 = 12,5 watts

Exemple 13-3

Si on raccorde la bobine de l'exemple 13-2 à une source de 100 V au lieu de 50V quelles seront la nouvelle FMM et la nouvelle puissance dissipée?

Solution

La tension étant doublée, le courant sera également doublé à 0,5 A ; la FMM deviendra:

FMM = 0,5 x 5000 = 2500A

La puissance dissipée deviendra:

P = 0,5 x 100 = 50 watts

En doublant la tension, on double la FMM, mais on quadruple la puissance dissipée en chaleur.

Ce résultat est très important car il nous fait réaliser que l'on ne peut pas obtenir une FMM plus grande sans risquer de détériorer l'isolant de la bobine par la température élevée, due au dégagement accru de la chaleur.

Exemple 13-4

Un électro-aimant comprend une bobine constituée de 3000 spires de fil #27. La bobine fonctionne normalement sous une tension de 120 V et tire un courant de 0,4 A.

On désire la rebobiner pour servir sous 240 V. Quel devra-être le nombre de spires et la grosseur du fil, sachant que les dimensions de la bobine ne doivent pas être changées?

L'électro-aimant deviendra-t-il plus puissant?

Solution

Puisque la bobine doit avoir les mêmes dimensions, la puissance dissipée en chaleur doit demeurer la même afin de garder le même échauffement.

Sous 120 V, la puissance dissipée était:

P= E x I=120 x 0,4= 48W

Sous 240 V, la puissance demeurant la même, le courant sera:

I = P/E = 48 / 240 = 0,2A

Le courant étant diminué de moitié, on pourra utiliser un fil dont la section sera deux fois plus petite que celle du #27, soit un fil #30.

Pour un fil deux fois plus petit, il sera possible de placer deux fois plus de tours sur la bobine, tout en conservant les mêmes dimensions.

Le nombre de tours sera porté à 2 x 3000 = 6000 tours . La FMM de la nouvelle bobine sera donc, sous 240 V, de 0,2A x 6000 spires = 1200 A, soit la même valeur que pour la première bobine.

Ce résultat est important: il est possible de rebobiner l'enroulement d'un électro-aimant à courant continu pour servir à une autre tension, sans changer ses dimensions, sa force magnétomotrice et sa température.

La FMM ne changeant pas, la puissance magnétique de l'électro-aimant reste la même.

Résumé

Cette section nous a présenté le premier principe de l'électromagnétisme, à savoir la création d'un champ magnétique par un courant. Tout conducteur parcouru par un courant s'entoure d'un champ magnétique. Les lignes de force suivent des cercles concentriques autour du conducteur.

Nous avons vu que la règle de la main droite permet de trouver facilement le sens de ces lignes de champ.

Pour un courant donné, la densité de flux en teslas à une distance donnée du centre du conducteur peut être calculée par une formule simple.

De la même façon, une spire, et plus généralement une bobine parcourue par un courant, est traversée par un flux magnétique dont les lignes sortent par une extrémité constituant le pôle nord et rentrent par l'autre extrémité constituant le pôle sud.

Le produit NI(nombre de spires x courant en ampères) est la force magnétomotrice développée par la bobine. Une bobine parcourue par un courant produit donc un champ magnétique tout comme un aimant permanent.

Cette propriété est mise à profit dans les électro-aimants constitués d'une bobine enroulée autour d'un noyau de fer doux. Sa perméabilité élevée permet d'amplifier des milliers de fois le champ magnétique créé par la bobine.

Les électro-aimants ont de nombreuses applications en électrotechnique : création de flux dans les pôles de moteurs et génératrices, disjoncteurs, freins, relais et sonneries.

PROBLÈMES

Niveau pratique

13-1 Comment peut-on démontrer l'existence d'un champ magnétique autour d'un conducteur portant un courant?

13-2 Donner la règle de la main droite indiquant le sens du champ magnétique en fonction du courant.

13-3 Quelle est l'unité SI de force magnétomotrice?

13-4 Dans la Fig. 13-26, en utilisant la règle de la main droite, donner la polarité magnétique de l'extrémité A du noyau de l'électro-aimant.

Figure 13-26 Voir problème 13-4

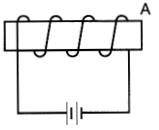
13-5 On applique une tension de 150 V à une bobine dont la résistance est de 120 S2. Sachant que la bobine a 1000 spires, calculer sa force magnétomotrice.

13-6 Le pôle nord d'une boussole est attiré par l'extrémité A d'une bobine (Fig . 13-27). Déterminer le sens du courant et la polarité électrique (+) (-) de la source.

Figure 13-27 Voir problème 13-6

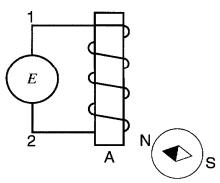
Niveau intermédiaire

13-7 Un électro-aimant est placé vis-à-vis d'un aimant permanent N-S (Fig. 13-28).

Figure 13-28 Voir problème 13-7

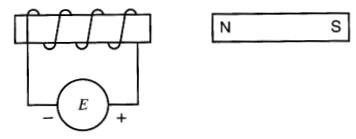
Si la source de tension a la polarité électrique indiquée, y aura-t-il attraction ou répulsion?

Qu'adviendra-t-il si les bornes de la bobine sont interverties?

13-8 Soit deux électro-aimants A et B branchés en série, et raccordés à une source de 60 volts (Fig . 13-29). La résistance de la bobine A est de 50Ω, celle de B, de 70Ω.

Figure 13-29 Voir problème 13-8

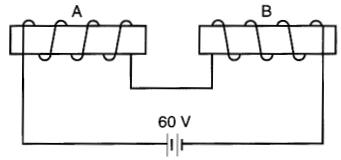
La bobine A a 2000 spires alors que la bobine B n'a que 800 spires.

Déterminer:

a) la FMM de chacune des bobines

b) la puissance dissipée dans chacune des bobines

c) si les deux bobines ont les mêmes dimensions, laquelle atteindra la plus haute température?

d) s'il y aura attraction ou répulsion entre ces deux électro-aimants?

13-9 Pourquoi un électro-aimant raccordé à une source de tension fixe devient-il moins puissant à mesure que sa bobine s'échauffe?

13-10 La bobine d'un électro-aimant est constituée de 5000 spires de fil #22, et elle est construite pour une tension nominale de 120 V. Sa résistance est de 120Ω.

S'il fallait la rebobiner pour qu'elle garde les mêmes propriétés magnétiques et thermiques sous une tension de 6 V, quel devrait être le calibre du fil et le nombre de spires à employer?

La bobine aurait-elle les mêmes dimensions?

Niveau avancé

13-11 Le câble d'aluminium de la Fig. 10-12c porte un courant de 343 A.

Calculer la densité de flux :

a) à la surface du conducteur toronné

b) à la surface extérieure du câble Note: mesurer avec une règle, le diamètre du conducteur et du câble.

13-12 Dans la Fig. 13-25b, vérifier que la FMM totale des enroulements principaux et auxiliaires est bien de 1,95 MA et 1,14 MA.

13-13 Calculer la longueur moyenne d'une spire de l'enroulement principal (Fig . 13-25b), en utilisant les données du tableau 13-1.

13-14 Si l'eau circulant dans les conducteurs creux de la Fig. 13-25 entre à une température de 12 °C et ressort à 40 °C, quel est le débit en litres par seconde?

13-15 Chacun des 36 pôles d'un alternateur de 500 MVA installé à Churchill Falls est composé de 21 spires de cuivre ayant une section de 11 x 88 mm. Les bobines ont une longueur de 3100 mm et une largeur de 700 mm.

Sachant que le courant d'excitation est de 2400 A et que les pôles sont raccordés en série, calculer:

a) la FMM par pôle

b) la tension d'excitation requise si la température des bobines est de 105 °C

c) la puissance d'excitation, en kW

Réponses

4) sud; 5) 1250 A; 6) 1 est positif; 7) répulsion; attraction si on inverse les bornes;
8a) A : 1000A; _B : 400A; 8b) A : 12,5W; 8 : 17,5W; 8c) B; 8d) répulsion;
10) 250 spires fil # 9; oui; 11 a) 9,1 mT; 11b) 3,2 mT; 13) 17,5 m;
14) 12,69 L/s; 15a) 50,4 kA; 15b) 327 V; 15c) 785 kW