Diagrammes vectoriels

Électrotechnique

Lors de la résolution des circuits à courant continu, on a eu recours aux lois de Kirchhoff
(section Solutions des circuits à courant continu). Les mêmes lois s'appliquent aux circuits à courant alternatif.

Cependant, comme les tensions et les courants sinusoïdaux ne sont pas nécessairement en phase et comme ils varient périodiquement en fonction du temps, il a fallu inventer une méthode simple pour résoudre ces circuits. Cette méthode repose sur le concept de vecteurs et de diagrammes vectoriels.

Somme de deux courants sinusoïdaux

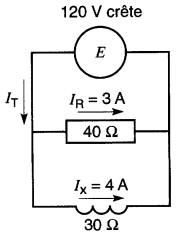
Soient une résistance de 40Ω et une réactance inductive de 30Ω branchées en parallèle sur une source de tension sinusoïdale de 120V (valeur crête). On désire connaître la valeur du courant I_T fourni par la source (Fig. 23-1).

Figure 23-1 Circuit composé d'une résistance en parallèle avec une réactance inductive. On cherche la valeur du courant IT

La tension étant la même aux bornes de chaque élément, le courant I_R dans la résistance et le courant I_x dans la réactance sont respectivement de 3A et de 4A 1valeurs crêtes). D'après les lois régissant les circuits à courant continu, on pourrait penser que le courant total I_T est de 3 + 4 = 7A.

Cependant, le courant I_x dans la réactance est déphasé de 90° en arrière de la tension tandis que le courant I_R dans la résistance est en phase avec la tension (Fig. 23-2).

Figure 23-2 Forme d'ondes de E, I_R et I_x La forme d'onde de I_T est obtenue en additionnant les valeurs instantanées de I_R et I_x

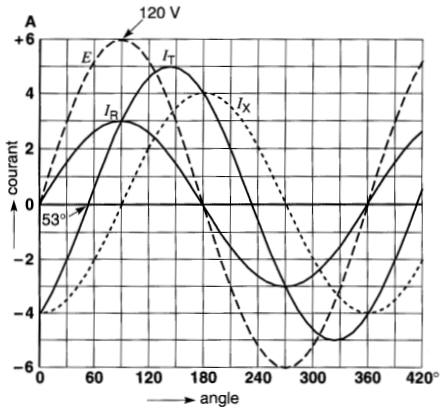
Pour connaître le véritable courant I_T résultant, il faut effectuer l'addition des courants I_R et I_x  à chaque instant.

Par exemple, à 60°:

I_R = 0,866 x 3A = +2,6A

I_x =0,50 x -4A=-2,0A

I_T = I_R et I_x = 2,6 -2,0 = 0,6A

En répétant cette addition à différents instants on trouve une nouvelle courbe sinusoïdale I_T dont la valeur crête est de 5A (Fig. 23-2).

De plus, cette courbe est décalée de 53° en arrière de la tension.

Dans cet exemple, la somme de 3A et 4A donne 5A et non pas 7A.

Cette méthode pour trouver la somme de deux courants alternatifs est laborieuse ; c'est pourquoi on a recours à un procédé graphique plus commode: la technique des vecteurs tournants.

Concept de vecteur tournant

Considérons deux axes perpendiculaires AB et CD qui se coupent au point O, soit à l'origine (Fig. 23-3a).

Figure 23-3a Un vecteur tournant à vitesse constante autour de l'origine génère une onde sinusoïdale

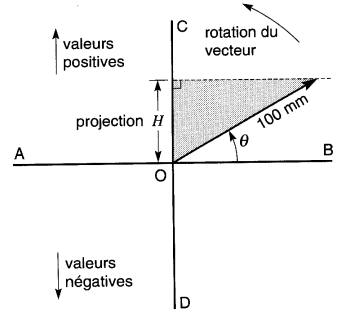
Imaginons une droite d'une longueur de 100 mm tournant autour du point O dans le sens antihoraire. La droite porte une flèche à l'extrémité opposée à l'origine.

On peut, à chaque position de la droite, mesurer l'angle de rotation 0 et la hauteur H correspondante projetée sur l'axe CD. Par exemple, lorsque l'angle est de 30°, la hauteur H mesure 50 mm, et quand l'angle est 90°, H mesure 100 mm.

Si l'on considère ces hauteurs comme étant positives lorsqu'elles sont au-dessus de l'axe AB et négatives quand elles sont en dessous, on peut dresser un tableau des hauteurs en fonction de l'angle (voir le tableau 23-1).

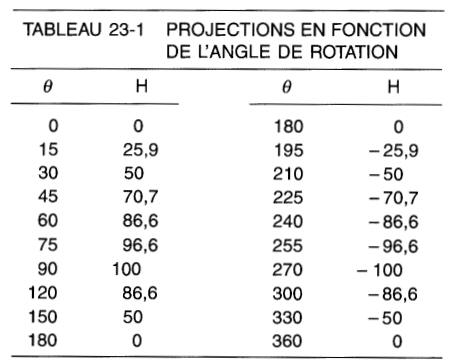
En traçant le graphique de H en fonction de 0, on obtient une onde sinusoïdale (Fig. 23-3b).

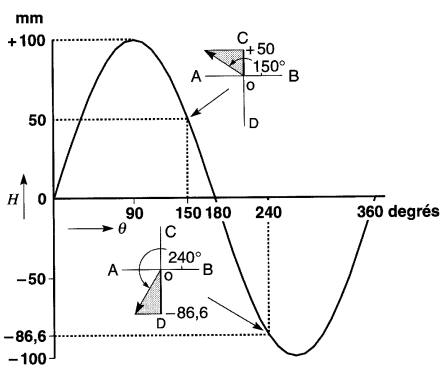
Il est évident que les valeurs des angles et des hauteurs se répètent chaque fois que la ligne droite (appelée vecteur) exécute un tour, de sorte que ce système possède une période semblable à celle d'une tension ou d'un courant sinusoïdal.

Ainsi, un vecteur de 170 mm de long tournant à une vitesse de 60 tours par seconde (60 r/s) peut représenter une tension de 170V crête, ayant une fréquence de 60 Hz.

Un cycle complet correspond à 360° mais, au fur et à mesure que le vecteur tourne, il passe par des valeurs d'angles bien supérieures à 360°.

Par exemple, un angle de 7350° correspond à 7350 - 360 = 20,4166 tours, soit (20 tours + 0,4166 tour), ce qui équivaut à 0,4166 x 360° = 150°.

Donc, un angle de 7350° génère la même hauteur H qu'un angle de 150°. Il est donc possible de représenter une tension sinusoïdale au moyen d'un vecteur tournant dont la longueur est égale à la valeur crête de la tension, et dont la vitesse de rotation correspond à la fréquence. Un courant sinusoïdal peut être représenté de la même manière.

Cette représentation des courants et des tensions par des diagrammes vectoriels facilite énormément la solution des circuits à courant alternatif.

En génie électrique, on adopte généralement comme valeur instantanée la projection du vecteur, non pas sur l'axe vertical CD, mais sur l'axe horizontal AB.

Dans cette section, nous avons décidé d'utiliser la projection sur l'axe vertical pour faciliter la visualisation du vecteur et de l'onde qu'il génère. Les deux méthodes de projection donnent exactement les mêmes résultats; en effet, il suffit de tourner les axes AB et CD de 90° dans le sens horaire pour arriver à la représentation classique utilisée par les ingénieurs.

 Représentation d'une tension sinusoïdale

La longueur d'un vecteur et sa vitesse de rotation décrivent respectivement sa valeur crête et sa fréquence. De plus, sa position sur un diagramme vectoriel sert à définir sa valeur initiale. Considérons, par exemple, le vecteur représentant une tension de 100 V crête dont la fréquence est 60 Hz (Fig. 23-4a).

Figure 23-4

a. Un vecteur peut représenter complètement une onde sinusoïdale b. Onde générée par le vecteur

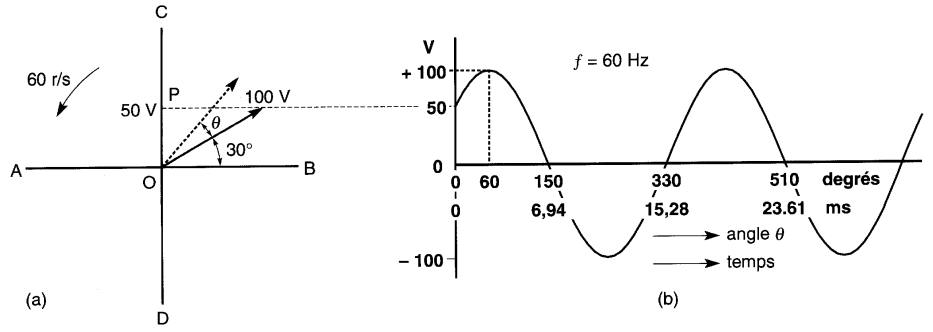
Il fait un angle de 30° avec l'axe horizontal AB ; sa projection sur la ligne CD est donc de 50V. Cette projection OP représente la valeur initiale de la tension. Le vecteur gras de la Fig. 23-4a représente alors la forme d'onde donnée à la Fig. 23-4b.

De façon générale, la valeur d'une grandeur (tension, courant, etc.) qui varie sinusoïdalement est donnée par l'équation:

ou

V = valeur instantanée de la grandeur
V_m = valeur crête de la grandeur
θ = angle exécuté à partir de t = 0, en degrés [°]
α = angle de déphasage, en degrés [°]
f = fréquence, en hertz [Hz]
t = temps, en secondes [s]
360 = constante tenant compte des unités

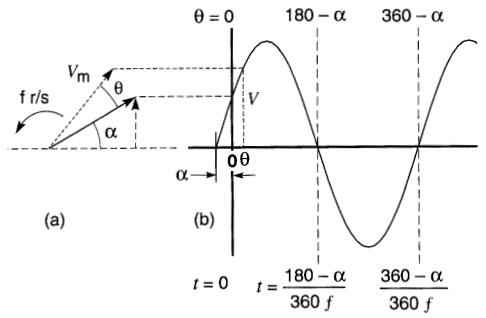
Cette équation peut être représentée graphiquement, soit par le vecteur gras de la Fig. 23-5a, soit par la forme d'onde de la Fig. 23-5b.

Figure 23-5 Diagramme vectoriel et forme d'onde correspondant à l'équation

V = V_m sin (θ + α) = = V_m sin (360 ft + α)

Exemple 23-1

Un courant sinusoïdal à 180 Hz a une valeur crête de 8A et un angle de déphasage de 240°.

Figure 23-6 Voir exemple 23-1

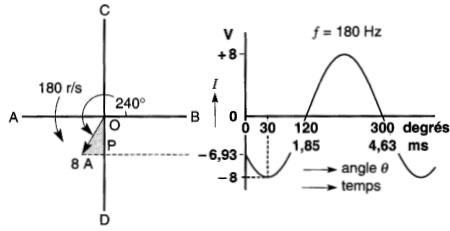
Déterminer.

a) L'expression algébrique du courant

b) la valeur instantanée du courant à t = 3,03 s

c) la valeur du courant lorsque l'angle θ= 210 °

d) tracer le diagramme vectoriel du courant et sa forme d'onde

Solution

a) L'expression algébrique du courant est donnée par la formule:

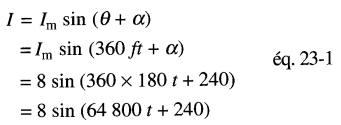
b) la valeur instantanée du courant à t = 3,63 s est :

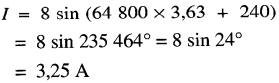
c) la valeur du courant à 0 = 210° est :

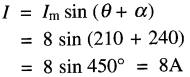
Représentation de plusieurs vecteurs Essayons d'appliquer la méthode des vecteurs au circuit de la Fig. 23-1. Rappelons que la tension E et le courant I_T sont respectivement de 1.20V et 5A et que le courant est décalé de 53° en arrière de la tension.

On peut représenter ces deux grandeurs par les vecteurs de la Fig. 23-7.

Figure 23-7 Représentation à l'échelle des vecteurs correspondant à E et I R de la figure 23-2

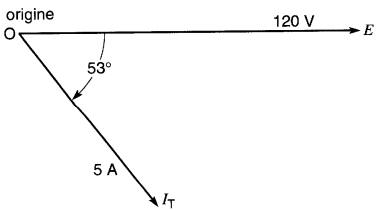
Pour construire ce diagramme vectoriel, on choisit d'abord une échelle convenable pour la tension et une autre pour le courant.

Ainsi, 1 mm pourrait représenter une tension de 2V de sorte que le vecteur de la tension (120V) aurait une longueur de 60 mm. De la même façon, 8 mm pourrait représenter un courant de 1A, de sorte que le vecteur de courant (5A) aurait une longueur de 40 mm.

Quelle position devons nous donner au vecteur de tension?

Nous avons arbitrairement choisi la position horizontale, avec la flèche orientée vers la droite.

Cependant, dès qu'on a choisi la position du vecteur E, celle du courant n'est plus arbitraire. En effet, la fréquence du courant et de la tension étant la même, les deux vecteurs tournent à la même vitesse, ce qui fait que le courant est toujours décalé de 53° en arrière de la tension, quelle que soit sa position.

Dans la Fig. 23-7 nous avons négligé la présence des axes AB et CD, tout en imaginant qu'ils existent en arrière-plan. On peut compléter ce diagramme en ajoutant les courants I_R et I_x de la Fig. 23-1, ce qui nous donne le diagramme vectoriel de la Fig. 23-8.

Figure 23-8 Représentation vectorielle de la tension et des courants de la figure 23-2

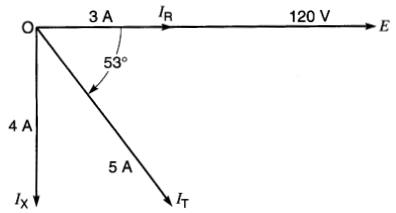
Noter que le vecteur I_R est en phase avec le vecteur de tension E alors que le vecteur I_x est décalé de 90° en arrière de E. La Fig. 23-8 représente donc la même information que les courbes de la Fig. 23-2; on réalise immédiatement la grande simplification apportée par le diagramme vectoriel.

Addition de vecteurs

Lors de la résolution des circuits à courant alternatif, on a souvent besoin de trouver la somme de deux vecteurs représentant deux tensions ou deux courants. Il est facile d'effectuer cette addition si l'on utilise une méthode graphique.

Supposons que l'on cherche la somme des tensions E₁ et E₂ représentées sur le diagramme vectoriel de la Fig. 23-9a.

Figure 23-9
a. Deux vecteurs que l'on désire additionner;
b. La somme vectorielle E₁ + E₂ donne le vecteur OP;
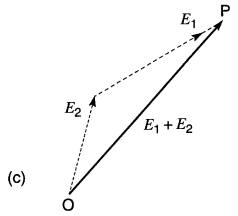
c. La somme vectorielle E₂ + E₁ donne le même vecteur OP.

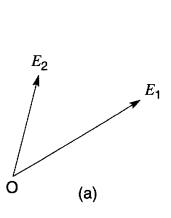
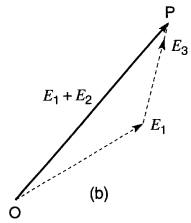
En se référant à la Fig. 23-9b, on procède de la manière suivante :

1. On choisit un des vecteurs, E₁ par exemple, comme vecteur de départ.

2 En partant de la flèche du vecteur E₁ on trace un vecteur E₃ ayant la même direction et la même longueur que le vecteur E₂.

3. La somme vectorielle (E₁ + E₂) est alors donnée par le vecteur OP qui part de l'origine O et aboutit à la flèche de E₃. On aurait pu commencer avec le vecteur E₂ et y ajouter le vecteur E₁ sans modifier le résultat final (Fig. 23-9c).

On utilise la même méthode pour trouver la somme de trois, quatre, ou plusieurs vecteurs.

Ainsi, sur la Fig. 23-10, la somme E₁ + E₂ + E₃ donne le vecteur E₄.

Figure 23-10 a. Trois vecteurs de tension que l'on désire additionner ; b. La somme vectorielle donne le vecteur E₄.

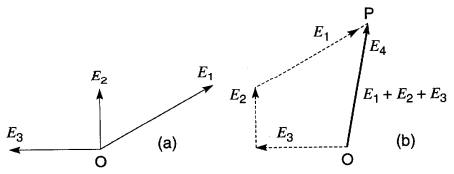
Pour trouver le vecteur résultant, on a suivi la chaîne E₃=> E₂=> E₁.

Exemple 23-2

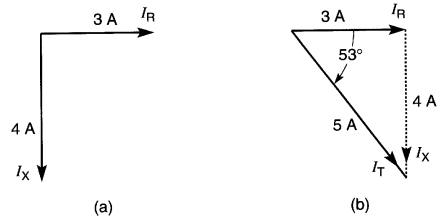
Trouver la somme vectorielle des courants I_R et l_X de la Fig. 23-11 a.

Figure 23-11 a. On cherche la somme vectorielle I_R et l_X  (exemple 23-2); b. La somme vectorielle donne un courant I_T de 5A déphasé de 53° en arrière de IR

Solution

Les courants ont respectivement une valeur crête de 3A et de 4A et ils sont décalés de 90°.

En traçant ces vecteurs à l'échelle, on trouve que leur somme vectorielle donne un courant I_T de 5A et un rapporteur révèle que l'angle θ est 53° (Fig. 23-1b). Cette méthode est beaucoup plus simple que la méthode laborieuse que nous avons utilisée pour trouver le courant I_T de la Fig. 23-2.

Vecteurs négatifs et soustraction de vecteurs

Dans certains cas, il faut soustraire un vecteur d'un autre; c'est alors que le concept de vecteur négatif est particulièrement utile.

Soit un vecteur E_a (Fig. 23-12).

Figure 23-12 Pour changer le signe d'un vecteur, on le fait tourner de 180°

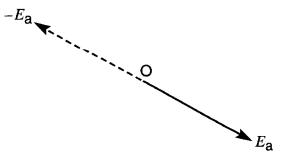
Le vecteur négatif -E_a (en pointillé) a la même longueur que E_a, mais il est dirigé dans le sens opposé.

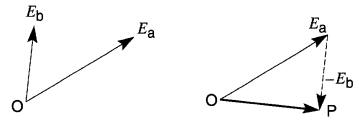
Si, dans la Fig. 23-13, on cherche la différence vectorielle E_a - E_b , on fait la somme E_a + (-E_b), ce qui donne le vecteur OP.

Figure 23-13 Soustraction de deux vecteurs

Vecteurs «détachés»

Jusqu'à présent, nous avons supposé que tous les vecteurs de tension et de courant tournent autour d'un point commun qui coïncide avec l'extrémité opposée à la flèche. Cependant, on peut détacher les vecteurs de cette origine commune sans pour autant changer leur amplitude ni leur angle de phase.

Par exemple, les vecteurs de la Fig. 23-7 peuvent être détachés de l'origine O, et représentés comme à la Fig. 23-14.

Figure 23-14 Vecteurs détachés

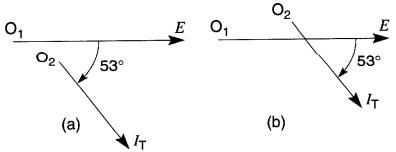
Le vecteur E est encore horizontal et il tourne autour de l'origine O₁. De plus, le vecteur I_T est toujours de 53° en arrière de E mais il tourne autour de son origine O₂.

Comme la position des origines est arbitraire, on peut tracer les vecteurs de plusieurs façons, comme, par exemple, celles de la Fig. 23-14.

Remarquer que si un système composé de plusieurs vecteurs tourne de 30°, tous les vecteurs tourneront de 30° autour de leurs origines respectives.

Comment trouver l'angle entre deux vecteurs détachés?

Imaginons qu'on fasse tourner un des vecteurs autour de son origine jusqu'à ce qu'il pointe dans la même direction que l'autre. L'angle de rotation correspond au déphasage entre les vecteurs, et le sens de rotation indique si le vecteur est en avant ou en arrière de l'autre.

Par exemple, si on doit faire tourner un vecteur A dans le sens horaire afin qu'il s'aligne avec un vecteur B, alors A est en avant de B.

Exemple 23-3

La génératrice à c.a. de la Fig. 15a produit trois tensions égales E₁₂, E₂₃, et E₃₁ entre ses bornes 1, 2 et 3.

Figure 23-15

a. Générateur produisant 3 tensions déphasées de 120° ;

b. Diagramme vectoriel des tensions

c. Autre manière de présenter le diagramme vectoriel

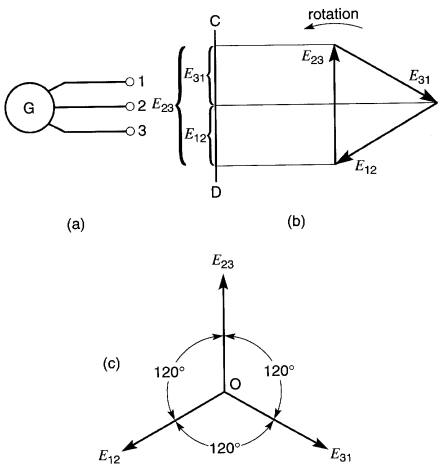
Ces tensions sont représentées par Lies vecteurs détachés disposés en forme de triangle (Fig. 2-3-15b).

Sachant que les trois tensions ont chacune une valeur crête de 200V.

Déterminer:

a) leur polarité et leur valeur instantanée lorsque

E₂₃ = + 200V (cas de la Fig. 23-15b)

b) le déphasage entre ces trois tensions

Solution

a) Les valeurs instantanées sont données par la projection des vecteurs sur l'axe vertical CD.

Les projections sont positives lorsque les vecteurs pointent vers le haut, et négatives lorsqu'ils pointent vers le bas.

E₂₃ = +200V; la borne 2 est positive par rapport à la borne 3;

E₁₂ = -100V; la borne 1 est négative par rapport à la borne 2;

E₃₁ = -100V; la borne 3 est négative par rapport à la borne 1.

b) Pour déterminer le déphasage entre les vecteurs, considérons d'abord les vecteurs E₃₁ et E₁₂.

Afin de les aligner, on doit faire tourner E₁₂ de 120° dans le sens antihoraire.

Par conséquent, E₁₂ est en arrière de E₃₁.

Cependant, il est plus facile de redessiner les trois vecteurs avec une origine commune (Fig. 23-15e);

on peut indiquer le déphasage de plusieurs manières, en voici quelques-unes :

E₂₃ est déphasé de 120° en arrière de E₁₂

E₁₂ est déphasé de 120° en avant de E₂₃

E₂₃ est déphasé de 240° en arrière de E₃₁

E₃₁ est déphasé de 120° en arrière de E₂₃ et ainsi de suite.

Vecteurs et phaseurs

Dans la résolution des circuits à courant alternatif, on utilise habituellement les valeurs efficaces des tensions et des courants. On peut alors employer des vecteurs dont la longueur correspond aux valeurs efficaces respectives.

Dans ce cas, les axes AB et CD (Fig. 23-3a) ne sont plus requis, car on ne s'intéresse pas aux valeurs instantanées des tensions et des courants. Toutefois, on trouve la somme ou la différence des vecteurs de la même manière.

Ces vecteurs qui ne tournent pas sont parfois appelés phaseurs (en anglais «phasors»).

Exemple 23-4

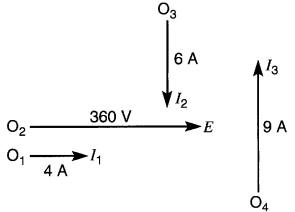
Tracer le diagramme vectoriel pour le circuit de la Fig. 23-16.

Figure 23-16 Circuit composé de trois éléments. On cherche le courant IT (voir exemple 23-4)

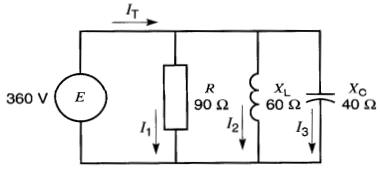
Trouver la valeur efficace du courant 'T et son déphasage par rapport à la tension E. La tension de la source est de 360V efficace.

Solution

Dans ce circuit, la tension est commune aux trois éléments R, XL et Xc.

Par conséquent, nous la choisissons comme vecteur de référence. On la trace donc dans le sens horizontal en utilisant une échelle appropriée (1 mm = 6V). À partir de ce vecteur de référence, on trace les vecteurs I₁ , I₂ et I₃.

I₁ = 360V / 90Ω = 4A, en phase avec E, car l'élément est résistif. (On utilise l'échelle 3 mm = 1A.)

I₂ = 360V / 60Ω = 6A, 90° en arrière de E, car l'élément est inductif.

I₃ = 360V / 40Ω= 9A, 90° en avant de E, car l'élément est capacitif.

Le courant I_T est la somme vectorielle des courants I₁ , I₂ et I₃.

D'après la construction graphique, on mesure I_T  = 15 mm, soit 5A efficace. Un rapporteur indique que I_T  est déphasé de 37° en avance sur E (Fig. 23-17).

Figure 23-17 Diagramme vectoriel du circuit (voir exemple 23-4)

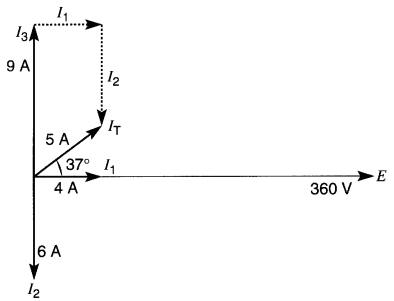
On observe que le courant fourni par la source (5A) est inférieur à celui circulant dans le condensateur (9 A) et dans l'inductance (6A).

C'est un phénomène nouveau, bien différent de ce que nous avons rencontré dans les circuits à courant continu. La Fig. 23-18 montre les mêmes phaseurs que ceux de la Fig. 23-17, sauf qu'ils sont détachés les uns des autres. On constate que I₂ est encore 90° en arrière de E, alors que I₁ est en phase avec E.

Figure 23-18 Diagramme vectoriel de la Fig. 23-17, montrant les vecteurs sous forme détachée

CALCUL VECTORIEL

On peut résoudre la plupart des circuits à courant alternatif en utilisant la méthode graphique exposée dans cette section.

Cependant, pour décrire les vecteurs, il est souvent plus pratique d'utiliser une expression mathématique plutôt qu'une représentation purement graphique. Le calcul vectoriel permet de trouver facilement la somme ou la différence de deux vecteurs. Il permet aussi de trouver le produit ou le quotient de deux vecteurs.

Par la suite, cette méthode permet de calculer l'impédance d'un circuit et les puissances active et réactive qu'il consomme. Le calcul vectoriel exige seulement une connaissance élémentaire de la trigonométrie. Les paragraphes qui suivent expliquent les règles de base de cette méthode de calcul.

Représentation polaire d'un vecteur

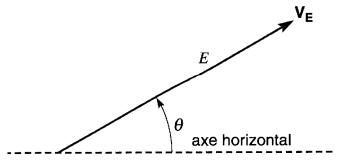
Considérons un vecteur VE de tension ayant une valeur efficace E, et faisant un angle 6 avec l'axe horizontal (Fig. 23-19).

Figure 23-19 Représentation polaire d'un vecteur

On peut le représenter sous la forme polaire par l'expression:

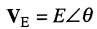    (23-2)

ou

V_E = vecteur de tension

E = valeur efficace de la tension

θ = angle entre le vecteur et l'axe horizontal

Noter que le symbole utilisé pour le vecteur est donné en caractère gras.

La Fig. 23-20 donne deux autres exemples de la représentation polaire.

Figure 23-20

a. L'angle est positif lorsqu'il est mesuré dans le sens antihoraire;

b. l'angle est négatif lorsqu'il est mesuré dans le sens horaire

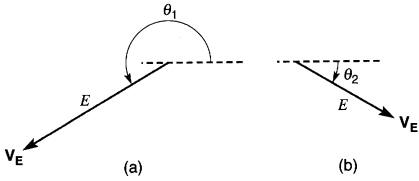
Dans cette figure, l'angle θ₁ est positif parce qu'il est mesuré dans le sens antihoraire à partir de l'axe horizontal.

Par contre, l'angle θ₂ est négatif parce qu'il est mesuré dans le sens horaire. Ainsi, le vecteur IT de la Fig. 23-7 serait désigné :

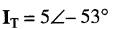
tandis que celui de la Fig. 23-17 serait désigné :

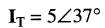
Nous utiliserons toujours la forme polaire pour multiplier ou diviser deux vecteurs.

Représentation rectangulaire d'un vecteur

On peut imaginer qu'un vecteur est composé de la somme vectorielle de deux vecteurs, l'un qui est parallèle à l'axe horizontal et l'autre qui lui est perpendiculaire.

Par exemple, les vecteurs V₁ , V₂, V₃, V₄ de la Fig. 23-21 sont tous composés de deux vecteurs V_H et V_p.

Figure 23-21 Le vecteur V est composé d'un vecteur horizontal et d'un vecteur vertical

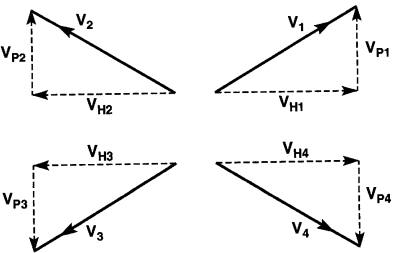
Les vecteurs V_H sont positifs lorsqu'ils pointent vers la droite, et négatifs lorsqu'ils pointent vers la gauche.

Ainsi, les vecteurs V_H1 et V_H4 sont positifs, alors que V_H2 et V_H3 sont négatifs. De la même façon, les vecteurs Vp sont positifs lorsqu'ils pointent vers le haut, et négatifs lorsqu'ils pointent vers le bas.

Par conséquent, les vecteurs V_P1 et V_P2 sont positifs, tandis que V_P3 et V_P4 sont négatifs. Afin de distinguer les vecteurs verticaux des vecteurs horizontaux, on ajoute le préfixe j à tous les vecteurs verticaux.

Le lecteur familier avec la théorie des nombres complexes reconnaîtra que le symbole j représente √-1

Ainsi, dans la Fig. 23-22a, le vecteur V₁ est composé du vecteur horizontal ayant une longueur «a» et d'un vecteur vertical ayant une longueur «b».

Figure 23-22 Représentation rectangulaire d'un vecteur

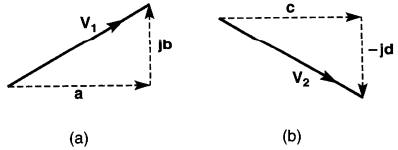
Le vecteur V₁ est donc la somme vectorielle des vecteurs a et jb, soit:

V₁ =a + jb

De la même façon, le vecteur V₂ (Fig. 23-22b) est donné par la somme:

V₂ =c - jd

Nous utiliserons toujours la forme rectangulaire pour additionner ou soustraire deux ou plusieurs vecteurs.

Conversion polaire -> rectangulaire

Nous avons mentionné qu'on utilise la forme polaire pour multiplier ou diviser les vecteurs, alors qu'on utilise la forme rectangulaire pour les additionner ou les soustraire.

Afin d'effectuer toutes ces opérations, on doit établir une méthode permettant de convertir les vecteurs d'une forme à l'autre.

Considérons le vecteur V dont l'amplitude est A, incliné à un angle 0 (Fig. 23-23).

Figure 23-23 Relation entre les formes polaire et rectangulaire d'un vecteur

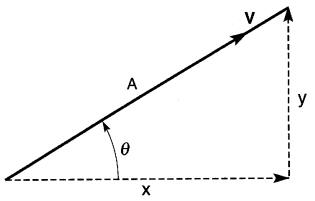
On peut écrire sous la forme polaire:

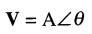
D'autre part, en utilisant la forme rectangulaire, on obtient:

V = x + jy

La composante horizontale de V a une amplitude x donnée par:

x = Acosθ

De même, la composante verticale de V a une amplitude y donnée par:

y =Asinθ

On peut donc écrire:

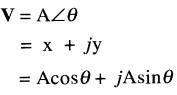
soit

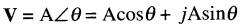    (23-3)

où

V = le vecteur (ou phaseur)

A = amplitude du vecteur

θ = angle entre le vecteur et l'axe horizontal

Acosθ = composante horizontale du vecteur

Asinθ= composante verticale du vecteur

Le symbole j qui précède l'expression Asinθ veut simplement dire que ce vecteur est perpendiculaire à l'axe horizontal.

Exemple 23-5

Un vecteur V est exprimé par la forme polaire :

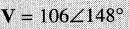
Exprimer ce vecteur sous la forme rectangulaire.

Solution

La forme rectangulaire est donnée par:

V = x + jy = Acosθ + jAsinθ = 106 cos 148° + j 106 sin 148°

= 106 x (-0,848) + j 106 x 0,53 = -90+j56

Par conséquent,

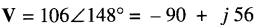
Conversion rectangulaire -> polaire

Supposons maintenant que le vecteur V soit donné sous la forme rectangulaire et qu'on désire l'exprimer sous la forme polaire.

On procède comme suit:

V = x + jy

En se référant à la Fig. 23-23 on constate que l'amplitude du vecteur est donnée par:

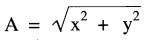    (Pythagore)

De plus, l'angle 0 est donné par :

θ = arctan (y/x)

Par conséquent, la forme polaire est donnée par:

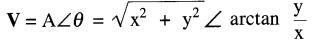    (23-4)

ou

V = le vecteur

A =amplitude du vecteur

θ = angle entre le vecteur et l'axe horizontal

x = composante horizontale du vecteur

y = composante verticale du vecteur

Note: Lorsque x est négatif, ont doit ajouter 180° à l'angle θ = arctan y/x indiqué par une calculatrice

Exemple 23-6

Un vecteur V est exprimé sous la forme rectangulaire:

V = 35 + j12

Exprimer cc vecteur sous la forme polaire.

Solution

L'amplitude du vecteur est :

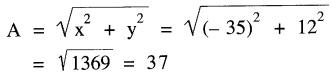
l'angle du vecteur est:

θ = arctan y/x = arctan 12 / -35 = arctan (-0,3428) = -19° + 180° = 161 °

Remarquer qu'on a dû ajouter 180° à l'angle calculé par arctan car la composante x est négative.

Par conséquent, la forme polaire du vecteur est:

V = 372161°

Conjugué d'un vecteur

Lors du calcul des puissances active et réactive dans un circuit à courant alternatif, on utilise le conjugué d'un vecteur. Soit un vecteur donné par la forme polaire:

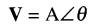
Par définition, le conjugué V* du vecteur (identifié par un astérisque) est alors :

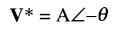
Le conjugué d'un vecteur est un vecteur de même longueur, mais dont l'angle est mesuré dans le sens contraire à celui du vecteur original.

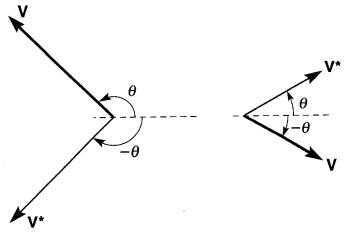
La Fig. 23-24 donne deux exemples d'un vecteur et de son conjugué.

Figure 23-24 Vecteur V et son conjugué V*

Addition des vecteurs

Soient deux vecteurs donnés par:

V₁ =a+ jb et V₂ =c+ jd

La somme vectorielle donne un nouveau vecteur V :

V = V₁ + V₂ = a + jb + c + jd = (a + c) + j (b + d)

C'est dire que la composante horizontale du vecteur V est égale à la somme des composantes horizontales de V₁ et de V₂.
De même, la composante verticale du vecteur V est égale à la somme des composantes verticales de V₁ et de V₂.

Exemple 23-7

Il s'agit de trouver la somme des deux vecteurs de la Fig. 23-25a,

Figure 23-25

a. Forme rectangulaire de deux vecteurs (voir exemples 23-7, -8, -9) ;

b. Addition des vecteurs

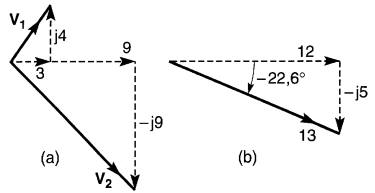
définis comme suit :

V₁ = 3 + j4

V₂ = 9 - j9

Calculer:

a) les composantes horizontale et verticale du vecteur résultant

b) l'amplitude et l'angle de phase du vecteur résultant

c) la forme polaire du vecteur

Solution

a) Le vecteur résultant est :

V = V₁ + V₂ = 3 + j4 + 9 - j9 = 12 - j5

La composante horizontale (x) est 12; la composante verticale (y) est -5. Le vecteur résultant est montré à la Fig. 23-25b.

b) L'amplitude du vecteur résultant est:

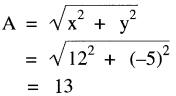
L'angle est:

θ = arctan y/x = arctan -5 / 12 = - 22,6°

c) La forme polaire du vecteur résultant est :

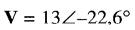
Multiplication des vecteurs

Soient deux vecteurs donnés par:

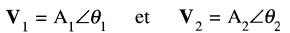
Le produit de deux vecteurs donne un nouveau vecteur dont l'amplitude est égale au produit A 1 A2 des amplitudes. L' angle est égal à la somme (θ₁ + θ₂ ) des angle.

Par conséquent, le produit des vecteurs est un noue vecteur V donné par:

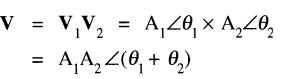
on a donc

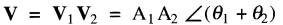    (23-5)

où

V₁ , V₂ = produit des deux vecteurs

A₁ , A₂ = amplitudes respectives des vecteurs

θ₁ , θ₂ = angles respectifs des vecteurs

V = vecteur résultant

 Exemple 23-8

Trouver le produit des vecteurs montrés à la Fig 23-25a, soient:

V₁ = 3 + j4

V₂ = 9 - j9

Solution

Afin de trouver le produit des vecteurs, on doit d'abord les transformer dans la forme polaire.

Pour V₁ on a:

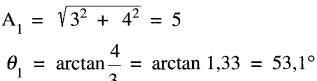
donc

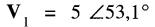
Pour V₂ on a:

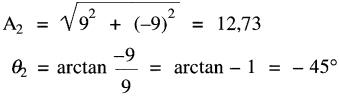
Donc

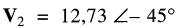
Par conséquent, le produit donne :

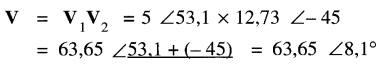
Division de deux vecteurs

Soient deux vecteurs exprimés par:

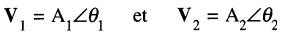
La division de V₁ par V₂ donne un nouveau vecteur V dont l'amplitude A et l'angle θ sont :

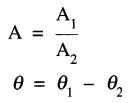
C'est dire que:

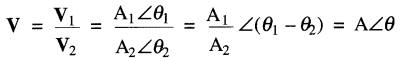
on a donc:

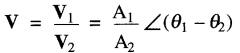    (23-6)

où les symboles ont la même signification qu'auparavant.

Exemple 23-9

Calculer l'amplitude et l'an e de phase du vecteur résultant de la division de V 1 par V, (Fig. 23-25a).

Solution

On vient de trouver dans l'exemple 23-8 que :

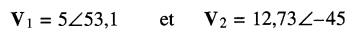
Par conséquent:

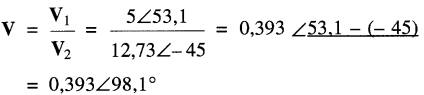
Ceci complète les règles concernant la manipulation des vecteurs. Appliquons maintenant le calcul vectoriel aux circuits électriques.

Impédance d'un circuit

Nous avons déjà vu à la section ci-haut que la tension d'une source et le courant qu'elle fournit sont souvent déphasés. L'angle de déphasage dépend de la nature de la charge.

Dans la Fig. 23-26a, nous supposons que la charge Z est composée d'un groupement de résistances, d'inductances et de condensateurs raccordés de façon quelconque.

Figure 23-26

a. Circuit électrique généralisé ;

b. Relations vectorielles entre E, I, dans un circuit à courant alternatif

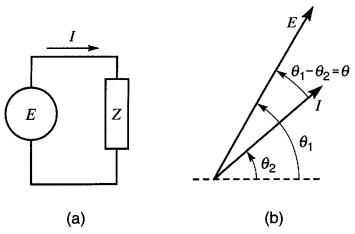
 La tension aux bornes de la charge est E et le courant résultant est I. Comme dans le cas d'une résistance, le rapport E/I est une mesure de l'opposition que la charge offre au passage du courant. Dans les circuits à courant alternatif, le rapport E/I généralisé s'appelle impédance.

Supposons que la tension soit exprimée par le vecteur :

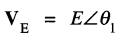
et que le courant soit donné par le vecteur:

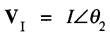
où E, I sont les valeurs efficaces de la tension et du courant (Fig. 23-26b).

L'impédance Z du circuit est alors:

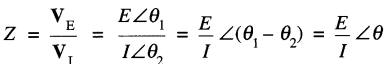
On constate que l'impédance est aussi un vecteur dont l'amplitude est E/I et que l'angle θ est celui compris entre le vecteur tension et le vecteur courant (Fig. 23-26b).

Si l'on exprime l'impédance sous la forme rectangulaire, on obtient :

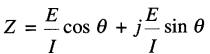
Trouvons maintenant, à tour de rôle, l'impédance d'une résistance, d'une réactance inductive et d'une réactance capacitive.

Impédance vectorielle d'une résistance

On sait que pour une résistance, l'angle θ entre la tension et le courant est nul. Par conséquent, on peut écrire :

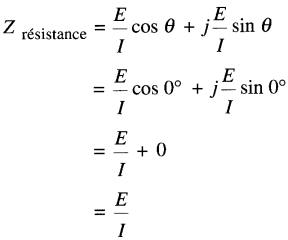
Le rapport E/I est simplement égal à la résistance R, de sorte que nous pouvons écrire :

Z_résistance = R    (23-7)

En d'autres mots, le vecteur représentant une résistance a une longueur R et il est dirigé vers la droite sur l'axe horizontal.

Impédance vectorielle d'une réactance inductive

On se souvient que pour une inductance la tension est 90° en avant du courant. Par conséquent, θ = +90°, ce qui nous permet d'écrire:

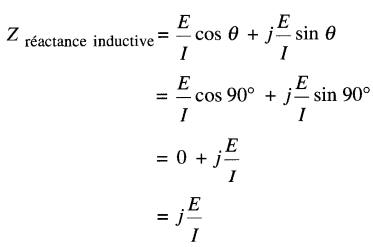
Comme le rapport E/I est simplement la valeur de la réactance inductive X_L, on peut écrire:

 Z_résistance = Z_L = jX_L     (23-8)

Une réactance inductive est donc un vecteur d'amplitude X_L, dirigé verticalement vers le haut.

Impédance vectorielle d'une réactance capacitive

Dans le cas d'une réactance capacitive, la tension est 90° en arrière du courant.

Par conséquent, θ = -90°, ce qui nous permet d'écrire :

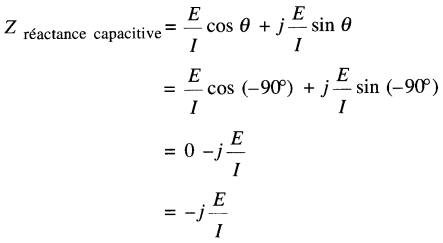
Puisque le rapport E/I est égal à la valeur de la réactance capacitive X_c on peut écrire:

Z_{résistance capacitive} = Z_c = -jX_c    (23.9)

Une réactance capacitive est donc un vecteur d'amplitude X_c, dirigé verticalement vers le bas. La représentation vectorielle de R, Z_L et Z_c est très utile dans la résolution des circuits à courant alternatif. Nous l'appliquerons dans les sections qui suivent.

Résumé

Dans cette section, nous avons appris qu'une grandeur sinusoïdale comme une tension ou un courant peut être représentée par un vecteur tournant.

Lorsque ces vecteurs sont représentés graphiquement, ils forment un diagramme vectoriel. Chaque vecteur peut aussi être exprimé par deux nombres, soit sous forme rectangulaire (composante horizontale et composante verticale), soit sous forme polaire (valeur efficace et angle).

On définit aussi l'impédance vectorielle d'une résistance, d'une réactance inductive et d'une réactance capacitive. Le calcul vectoriel permet de généraliser les techniques de solution des circuits à courant continu aux circuits à courant alternatif.

Nous avons appris comment effectuer les opérations d'addition, soustraction, multiplication et division sur les vecteurs représentant des tensions, courants et impédances.

Pour l'addition et la soustraction, il est plus commode d'utiliser les vecteurs sous forme rectangulaire. Par contre, pour les opérations de multiplication et de division on utilise la forme polaire.

PROBLÈMES

23-1 Une tension sinusoïdale de 60 Hz possède une valeur crête de 200V.

Dessiner le vecteur correspondant à cette tension en utilisant l'échelle 1 mm = 2V.

a) Quelle est la longueur du vecteur?

b) À quelle vitesse le vecteur tourne-t-il, en tours par seconde?

c) Quel est le temps requis pour exécuter un tour?

23-2 Répétez le problème 23-1 pour une tension de 4 Hz dont la valeur crête est de 80V.

23-3 Répétez le problème 23-1 pour un courant ayant une valeur efficace de 42,4A et une fréquence de 5 kHz. (La projection du vecteur sur l'axe vertical doit donner la valeur instantanée du courant.)

23-4 Les vecteurs représentant les tensions et les courants électriques tournent tous dans le sens conventionnel. Quel est ce sens de rotation conventionnel?

23-5 Une tension de 50 Hz ayant une valeur crête de 400 V est représentée par un vecteur dont la longueur est de 100 mm.

a) Doit-on tracer ce vecteur dans le sens horizontal, vertical ou à un angle quelconque?

b) Calculer le temps requis pour que le vecteur tourne d'un angle de 360°.

c) Calculer le temps requis pour que le vecteur tourne d'un angle de 90°, 30°, 2°, 2700°.

23-6 Un courant sinusoïdal de 50 Hz ayant une valeur crête de 12mA est représenté par un vecteur ayant une longueur de 60 mm.

a) Quelle est l'échelle utilisée?

b) De combien de degrés le vecteur tourne-t-il dans un intervalle de 5 ms? de 100 µs? de 2 s?

23-7 Deux tensions E_a et E_b ayant une valeur crête de 200V possèdent respectivement une fréquence de 50 Hz et de 40 Hz.

L'angle entre ces deux tensions est initialement nul.

a) De combien de degrés les vecteurs tournent-ils, respectivement, dans un intervalle de 5 ms? de 195 ms?

b) Quel est le déphasage entre les tensions E_a et E_b après un intervalle de 5 ms? de 195 ms?

23-8 En choisissant les échelles 1 mm = 2V et 5 mm = 1A, tracer les diagrammes vectoriels correspondant aux tensions et courants efficaces suivants :

a) tension de 160V déphasée de 90° en avant d'un courant de 10A

b) courant de 6A déphasé de 30° en arrière d'une tension de 120V

c) courant de 18A déphasé de 150° en avant d'une tension de 60V

d) tension de 200V déphasée de 690° en arrière d'un courant de 8A

23-9 En se référant à la Fig. 23-27, trouver la grandeur du vecteur résultant et son déphasage par rapport au courant I₂ lorsqu'on fait les sommes vectorielles suivantes:

Figure 23-27 Voir problèmes 23-9, 23-14, 23-15

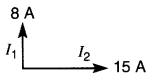
a) I₁ + I₂

b) I₁ -I₂

c) -I₁ + I₂

d) -I₁ - 1₂

(Prendre une échelle appropriée et utiliser une solution graphique.)

23-10 En se référant à la Fig. 23-28, trouver la grandeur du vecteur résultant et son déphasage par rapport au courant I₃ lorsqu'on fait les sommes vectorielles suivantes:

Figure 23-28 Voir problèmes 23-10, 23-16

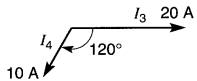
a)I₃ + I₄

b)I₃ - I₄

c) -I₃ + I₄

d) -I₃ - I₄

(Prendre une échelle appropriée et utiliser une solution graphique.)

23-11 En se référant à la Fig. 23-29, trouver la grandeur du vecteur résultant et son déphasage par rapport à la tension E₂ lorsqu'on fait les sommes vectorielles suivantes:

Figure 23-29 Voir problème 23-11

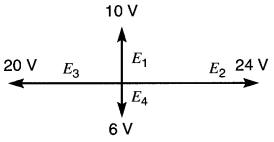
a) E₁ + E₂ + E₃ + E₄

b) E₁ + E₂ + E₃ - E₄

C) E₁ - E₂ + E₃ - E₄

d) -E₁ + E₄

(Prendre une échelle appropriée et utiliser une solution graphique.)

23-12 Dans la Fig. 23-27, exprimez les vecteurs dans la forme polaire.

Niveau intermédiaire

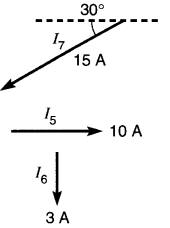
 23-13 Trouver la somme vectorielle des vecteurs de la Fig. 23-30.

Figure 23-30 Voir problèmes 23 -13, 23-17

23-14

a) Tracer la forme d'onde représentée par vecteur I₁ de la Figure 23-27 sachant que 8 A représente la valeur crête du courant et que les valeurs instantanées sont données par la projection sur l'axe vertical.

b) Quelle est la valeur instantanée du courant aux angles suivants : 0°? 90°? 240°?

23-15

a) Tracer la forme d'onde représentée par le vecteur I₂ de la Fig. 23-27, sachant que 15 A représente la valeur crête.

b) Quelle est la valeur instantanée du courant aux angles suivants: 0°? 90°? 270°?

23-16

a) Tracer la forme d'onde représentée par le vecteur I₄ de la Fig. 23-28, sachant que 10A représente la valeur crête et que la fréquence est de 50 Hz.

b) Calculer la valeur instantanée du courant aux angles suivants: 0°, 30°, 120°.

c) Calculer la valeur instantanée du courant aux instants suivants: 0,5 ms, 10 ms, 955 ms.

23-17 Dans la Fig. 23-30, quel est le déphasage :

a) de I₆ par rapport à I₅?

b) de I₆ par rapport à I₇?

c) de I₇ par rapport à I₅?

23-18 Dans la Fig. 23-31, quel est le déphasage:

a) de E₁₂ par rapport à E₃₁ ?

b) de E23par rapport à E₃₁?

c) de E₁₂ par rapport à E₂₃?

23-19

a) Tracer sur un même graphique les formes d'ondes des tensions E₁₂, E₂₃, E₂₃ (Fig. 23-31), sachant que la fréquence est de 60 Hz et que les valeurs efficaces sont de 600V.

On supposera que E₁₂ = 0 V à t=0.

b) Quelles sont les polarités instantanées et les valeurs des tensions E₁₂, E₂₃, E₂₃ après 6 ms? après 100 ms? après 27 min?

Niveau avancé

23-20 Une tension sinusoïdale est exprimée par l'équation E = 850 sin (18 000 t + 90°).

Calculer la fréquence et tracer la forme d'onde.

23-21 Dans la Fig. 23-30 exprimer le vecteur I₇:

 a) sous la forme polaire

b) sous la forme rectangulaire

23-22 Une tension efficace est exprimée par le vecteur E= 8 -j15.

a) Exprimer ce vecteur sous la forme polaire.

b) Déterminer le conjugué du vecteur sous la forme rectangulaire.

23-23 Une tension est représentée par l'équation : E= 850 sin 18 000 t où l'angle est exprimé en degrés et t en secondes.

Calculer:

a) la fréquence de la tension

b) la valeur efficace de la tension

23-24 Dans la Fig. 23-15, la tension E₁₃ a une valeur instantanée de + 75V. Sachant que la fréquence est de 72 Hz,

calculer:

a) la valeur efficace de E₁₃

b) la valeur instantanée de E₁₃ 3 s plus tard

23-25 Dans la Fig. 23-31, les vecteurs représentent chacun une tension crête de 180V.

Exprimer le vecteur E₃₁ :

a) sous la forme polaire

b) sous la forme rectangulaire

23-26 Soient deux vecteurs donnés par: V₁ =63 + j16 et V₂ =-5 - j12

Calculer sous la forme polaire:

a) la valeur du produit des vecteurs

b) la valeur de V1/V2

Réponses

1a) 100 mm; 1b) 60 r/s; 1c) 16,67 ms; 2a) 40 mm; 2b) 4 r/s;

2c) 250 ms; 3a) 30 mm; 3b) 5000 r/s; 3c) 0,2 ms;

4) antihoraire; 5a) quelconque; 5b) 20 ms; 5c) 5 ms; 1,67 ms;
111 µs; 150 ms; 6a) 5 mm = 1 mA; 6b) 90°; 1,8°; 36 000°;
7a) Ea: 90°; 72°; Eb : 3510°; 2808°; 7b) Ea 18° en avant de Eb; Ea
18° en arrière de Eb; 9a) 17 A à + 28°; 9b) 17 A à + 152°;
9c) 17 A à -28°; 9d) 17A à -152°; 10a) 17,3 A à -30°;
10b) 26,5 A à + 19° ; 10c) 26,5 A à -161 °; 10d) 17,3 A à + 150°;
11a) 5,66 V à+ 45°; l l b) 16,5 V à+ 76°; l l c) 46,8 V à+ 160°;
11d) 16 V à -90° ; 12) 15 A à 0°; 8 A à+ 90°; 13) 10,9 A à 106° en
arrière de I5; 14b) + 8 A; 0 A; -4 A; 15b) 0 A; + 15 A; -15 A;
16b) -9,33 A; 8,66 A; 5 A; 16c) -8,66 A; -5A; +8,66 A;
17a) 90° en arrière; 17b) 60° en avant; 17c) 150° en arrière;
18a) 120° en arrière ; 18b) 120° en avant; 18c) 120° en avant;
19b) à 6 ms: E12 = + 654 V; E23 = + 141 V; E31 = -795 V;
à 100 ms : E12 = 0; E23 = -735 V; E31 = +735 V;
à 27 min : E12 = 0; E23 = -735 V; E31 = +735 V; 20) 50 Hz;
21 a) 15 à 210' ; 21 b) -13 -j 7,5; 22a) 17 Z -61,9°; 22b) 8 + j15;
23a) 50 Hz; 23b) 601 V; 24a) 106 V; 24b) 75 V; 25a) 180 à 120° ;
25b) -90 + j155,9; 26a) 845 à 261,6°; 26b) 5 à 126,8°