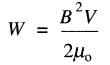Hystérésis et aimants permanents

Électrotechnique

On se souviendra que dans un matériau magnétique les domaines tendent à garder leurs orientations.

En effet, par une réaction semblable au frottement, les domaines s'opposent à tout changement d'orientation imposé par un champ extérieur; de même, une fois orientés, ils essaient de conserver leur orientation en s'opposant de nouveau à tout autre changement.

Ce phénomène, qu'on appelle hystérésis, est une propriété commune à tous les matériaux magnétiques. Ce phénomène d'hystérésis permet de réaliser des aimants permanents. Par contre, ce grand avantage est quelque peu assombri par les pertes que l'hystérésis occasionne dans un matériau magnétique parcouru par un flux alternatif.

Examinons d'abord la question des aimants permanents, en reportant à plus tard le sujet des pertes. Les aimants permanents d'aujourd'hui produisent des forces magnétomotrices très intenses de sorte que, à FMM égales, ils sont souvent plus petits que les électro-aimants qu'ils peuvent remplacer.

Comme ils n'ont besoin d'aucune source d'énergie extérieure pour maintenir leur magnétisme, les aimants permanents permettent de construire des appareils possédant un excellent rendement et des dimensions restreintes.

 Énergie magnétique dans l'air

Lorsqu'un flux magnétique est créé dans un milieu quelconque, il existe toujours une quantité d'énergie emmagasinée qui est récupérable.

Dans le cas d'un milieu comme l'air, ou de tout autre matériau non magnétique, la quantité d'énergie emmagasinée est bien définie et totalement récupérable.

En effet, tout comme on peut emmagasiner de l'énergie mécanique en comprimant un ressort, on peut emmagasiner de l'énergie magnétique en créant un champ magnétique. Comme toute autre forme d'énergie, l'énergie magnétique se mesure en joules.

Dans les matériaux non magnétiques comme l'air, la quantité d'énergie emmagasinée dépend de la densité de flux et du volume occupé par le champ. Sa valeur est donnée par la formule :

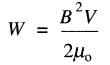    (15-1)

qui peut s'écrire sous la forme approximative

W = 400 000 B²V     (15-1a)

où

W = énergie dans le champ, en joules [J]

B = densité de flux, en teslas [T]

V = volume du champ, en mètres cubes [m³]

µ_o = 4π x 10^-7 ( = 1/800 000 environ)

Exemple 15-1

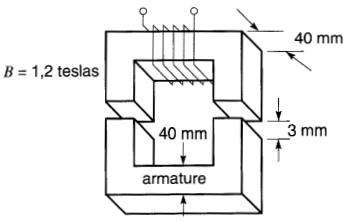
Un électro-aimant avant 2 pôles de 40 mm x 40 mm attire une armature à travers un entrefer de 3 mm (Fig. 15-1).

Calculer l'énergie W emmagasinée dans les deux entrefers si la densité de flux est de 1,2 T.

Figure 15-1 Énergie emmagasinée dans le champ magnétique d'un électro-aimant (exemple 15-1).

Solution

Le volume des deux entrefers vaut:

V = 2 x (40 x 40 x 3) = 9600 mm³

L'énergie magnétique emmagasinée dans les deux entrefers est:

W = 400 000 B²V éq.15-1a

= 400 000 x (1,2)² x 9600 x 10^-9 = 5,53 J

La «puissance» d'un aimant permanent dépend principalement de l'énergie magnétique qu'il peut conserver dans un champ magnétique à l'extérieur de ses parois.

Énergie magnétique dans un matériau magnétique

Pour une densité de flux donnée, l'énergie magnétique emmagasinée dans un matériau magnétique comme le fer est beaucoup plus faible que celle contenue dans un entrefer de même volume.

Sa valeur dépend de la forme de la courbe d'aimantation du matériau et de son niveau d'aimantation. À toutes fins utiles, dans un montage composé d'un noyau magnétique et d'un entrefer, l'énergie magnétique emmagasinée dans le noyau est négligeable.

Force d'attraction agissant sur un matériau magnétique

L'expérience nous montre qu'un matériau magnétique placé dans un champ magnétique subit une force d'attraction. La force agit toujours dans la direction des lignes de force, comme si elles étaient des élastiques attachés au morceau attiré.

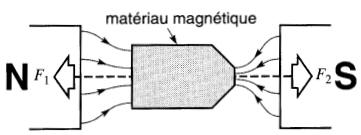
Par exemple, un morceau de fer placé entre les pôles d'un électro-aimant subit deux forces F₁ et F₂ qui tendent à attirer respectivement le morceau vers la gauche et vers la droite (Fig. 15-2).

Figure 15-2 Forces agissant sur un matériau magnétique lorsqu'il est placé entre les pôles N,S d'un électro-aimant (voir problème 15-15)

La valeur de la force F dépend de la densité de flux B et de la surface A traversée par le flux (Fig. 15-3).

Figure 15-3 La valeur de la force d'attraction dépend de la densité de flux B et de la section A traversée par le flux

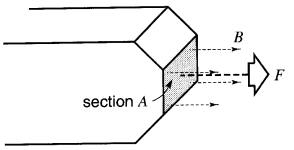
Sa valeur est donnée par l'expression:

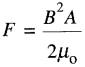    (15-2)

qui peut s'écrire sous la forme approximative

F = 400 000 B²A    (15-2a)

où

F = force d'attraction, en newtons [N]

B = densité de flux, en teslas [T]

A = section traversée, en mètres carrés [m²]

µ_o = 47t x 10^-7 (= 1/800 000 environ)

Exemple 15-2

Calculer la valeur de la force d'attraction F que l'électro-aimant de la Fig. 15-1 exerce sur son armature.

Solution

La surface A correspond ici à la surface des deux pôles de l'électro-aimant soit:

A = 2 x (40 x 40) = 3200 mm²

Comme B = 1,2 T, la force est donc:

F = 400 000 B²A     éq. 15-2a

= 400 000 x (1,2)² x 3200 x 10^-6 = 1843 N

La force d'attraction permet à cet aimant de soulever une masse de:

m = 1843 - 9,8 = 188 kg     éq. (1-1)

Remarquer que la force d'attraction dépend uniquement de la densité de flux à la surface de la pièce attirée; elle n'est pas affectée par le degré de saturation des autres parties du circuit magnétique.

De plus, la provenance du flux n'a aucune importance ; celui-ci peut être créé par la bobine d'un électro-aimant ou par un aimant permanent.

Densité de flux rémanent et champ coercitif

On a déjà vu à la section Circuits magnétiques que si l'on fait circuler un courant I dans une bobine entourant un tore magnétique (Fig. 15-4), la densité de flux B dans le circuit magnétique augmente avec le champ magnétique H.

Figure 15-4 Lorsqu'on fait varier le courant I dans la bobine, le champ magnétique H produit une densité de flux B. La courbe B-H est montrée à la Fig. 15-5

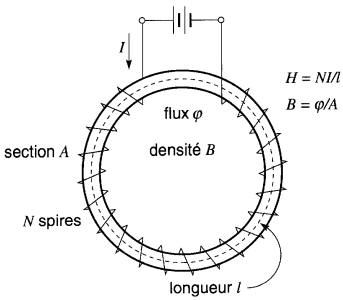
Si le flux initial est nul, cette augmentation suit la courbe Oa de la Fig. 15-5, la densité de flux atteignant la valeur Bm pour un champ magnétique Hm.

Figure 15-5 Courbe d'aimantation montrant le phénomène d'hystérésis, d'induction rémanente et de champ coercitif. La surface de la partie hachurée est l'énergie requise (en joules par mètre cube) pour désaimanter le matériau magnétique

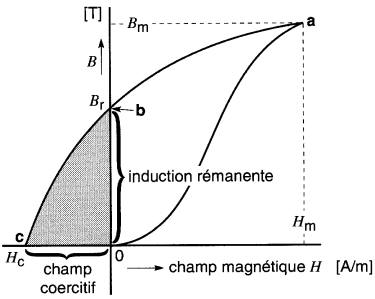
Si, maintenant, on fait décroître le courant I, c'est-à-dire le champ H, jusqu'à zéro, la densité de flux ne suit plus la même courbe, mais une courbe ab située au-dessus de oa.

En effet, quand on réduit le champ à zéro, les domaines que l'on vient d'orienter sous l'influence du champ Hm tendent à conserver cette orientation. C'est le phénomène d'hystérésis.

Donc, lorsque le champ H devient nul, une densité de flux subsiste et conserve une valeur Br que l'on appelle densité de flux rémanent ou induction rémanente.

Si l'on veut faire disparaître complètement ce flux rémanent, il faut renverser le sens du courant dans la bobine et faire croître le champ H jusqu'à une valeur Hc (courbe bc). Lorsqu'on décrit la portion de courbe bc, les domaines sont contraints de changer d'orientation les uns après les autres, jusqu'à ce que la densité de flux s'annule au point c.

Le champ magnétique H_c requis pour réduire le flux à zéro s'appelle champ coercitif. (1 T.A/m est équivalent à 1 J/m³)

Pour réduire la densité de flux de sa valeur Br jusqu'à zéro, il faut dépenser une certaine quantité d'énergie.

On peut prouver que l'énergie requise pour désaimanter 1 mètre cube de matériau est exactement égale à la surface hachurée comprise sous la courbe bc.

Par exemple, si cette surface (Fig. 15-5) vaut 100 teslas-ampères par mètre, on doit dépenser 100 joules d'énergie par mètre cube de matériau pour réduire le flux Br à zéro. Cette énergie est entièrement convertie en chaleur dans le matériau magnétique.

Elle représente le frottement qui se produit lorsque les domaines magnétiques reprennent leur orientation au hasard en passant du point b au point c sur la courbe.

En fait, un thermomètre très sensible indiquerait un léger échauffement du matériau magnétique lors de la désaimantation.

 Pour les matériaux «doux» comme le fer doux et l'acier employé dans les transformateurs, la quantité d'énergie requise pour les désaimanter est assez faible : de l'ordre de 10 J/m³.

Mais certains matériaux «durs» comme l' alnico requièrent des quantités d'énergie énormes: de l'ordre de 50 000 J/m³. C'est précisément cette énergie élevée qui distingue les matériaux à aimants permanents des autres matériaux magnétiques.

Idéalement, les matériaux utilisés pour la fabrication des aimants permanents doivent donc posséder, à la fois, une densité de flux rémanent (Br) élevée et un champ coercitif (Ha) de grande intensité de sorte que l'énergie requise pour les désaimanter soit aussi grande que possible.

Les courbes de désaimantation pour trois types d'aimants permanents, l'alnico V, l'Indox et l'acier au carbone sont montrées à la Fig. 15-6.

Figure 15-6 Courbes de désaimantation de trois matériaux utilisés dans les aimants permanents

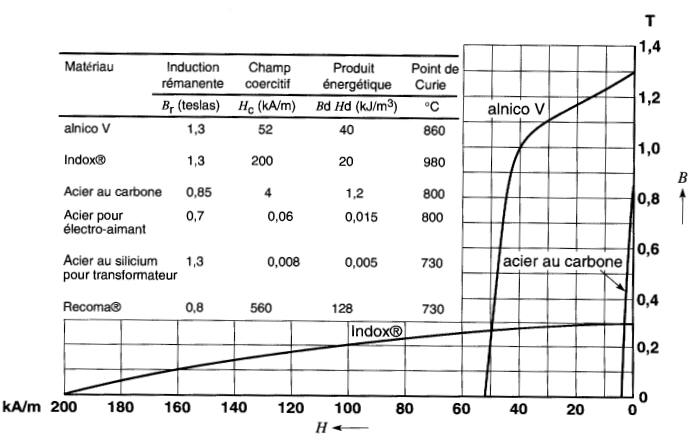
Elles représentent la portion bc de la courbe que nous venons de discuter.

On constate que l'alnico a une densité de flux rémanent de 1,3 T et un champ coercitif de 52 000 A/m.

La surface située en dessous de la courbe comprend environ 52 carreaux, ayant chacun une superficie de 1 carreau = 10 kA/m x 0,1 T = 1000 T.A/m L'énergie requise pour désaimanter l' alnico est donc W = 52 x 1000 T.A/m = 52 kJ/m³.

Types d'aimants permanents

Pour fabriquer des aimants permanents puissants, on a recours à divers alliages de substances de toutes sortes:

fer, aluminium, cobalt, cuivre, platine, yttrium, oxygène, carbone, etc.

Parmi les aimants à base de métaux, on connaît depuis longtemps l'acier trempé (1 % carbone, 0,5 % manganèse, 98,5 % fer) maintenant supplanté par des alliages tels que l' alnico V (8 % aluminium, 14 % nickel, 24 % cobalt, 3 % cuivre, 51 % fer).

Un aimant permanent en alnico V est presque 25 fois plus petit qu'un aimant en acier trempé créant le même champ. Découvert par hasard en 1932 par le physicien japonais I. Mishima, l'alnico, par sa dureté magnétique, a révolutionné l'industrie des dispositifs magnétiques.

En effet, pour la première fois, on pouvait réaliser un aimant permanent plus petit qu'un électro-aimant de même force. L'alnico est extrêmement dur et cassant si bien que l'on peut seulement changer sa forme en meulant les pièces coulées.

Les aimants à céramiques, une autre classe d'aimants, sont plus légers et possèdent une résistivité électrique équivalente à celle des bons isolants.

Ces aimants, portant des marques de commerce telles que Indox®, Arnox®, Vectolite®, Ferroxdure®, sont des ferrites composés d'un alliage d'oxyde de fer (Fe203), d'oxyde de baryum (BaO)6, d'oxyde de zinc, de cobalt, etc.

Ces aimants à céramiques possèdent une densité de flux rémanent Br plus basse que celle de l' alnico, mais développent des champs coercitifs H_c très élevés, de sorte que l'énergie requise pour annuler le flux rémanent est du même ordre de grandeur.

On rencontre ces matériaux dans les pièces polaires de certains moteurs, dans les bandes de caoutchouc servant à sceller les portes de réfrigérateurs et dans les bandes magnétiques pour enregistrement.

Enfin, depuis quelques années, les aimants les plus puissants sont ceux fabriqués avec du cobalt allié avec l'yttrium ou une des terres rares, comme le néodyme et le samarium. Notez, par exemple, les propriétés B_r et H_c du Recoma®, données à la Fig. 15-6.

Figure 15-6 Courbes de désaimantation de trois matériaux utilisés dans les aimants permanents.

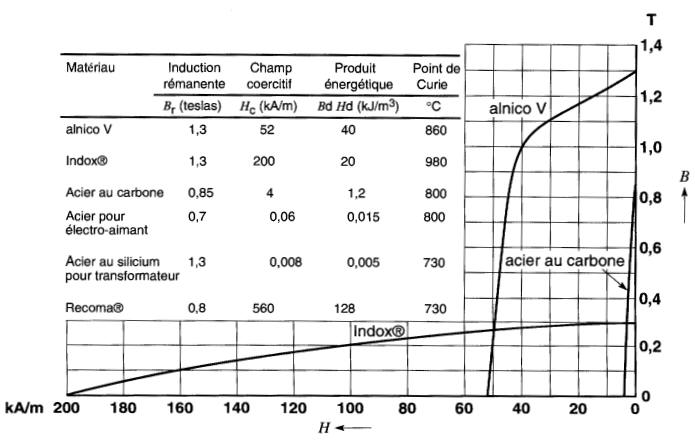
Pour un même volume, ils sont 3 fois plus puissants que les meilleurs aimants en alnico. Le seul inconvénient est leur coût relativement élevé.

FMM et flux d'un aimant permanent

La densité de flux rémanent B_r correspond à celle obtenue lorsque le matériau forme un circuit magnétique fermé (Fig. 15-4).

Cependant, un flux ainsi emprisonné dans un tore solide est inutile et, pour rendre ce flux accessible, on doit y ouvrir un entrefer.

En agissant ainsi, on observe que la densité de flux diminue graduellement à mesure que l'entrefer augmente, passant successivement par les points b, 1, 2, 3, sur la courbe de désaimantation B-H du matériau (Fig. 15-7).

Par contre, à mesure que la densité B diminue, le champ magnétique H augmente.

Figure 15-7 La longueur de l'entrefer détermine la valeur de B et H sur la courbe de désaimantation pour l'alnico V

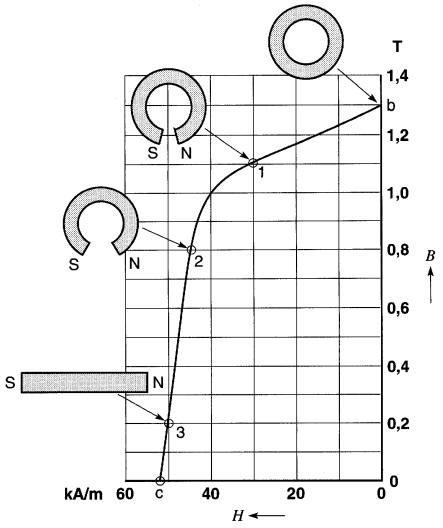
En effet, pour chaque valeur de B, l'aimant produit une valeur correspondante de H. Par exemple, en se référant à la courbe de désaimantation de l'alnico V (Fig. 15-7), on obtient les valeurs B, H suivantes:

B 1,3     1,1     0,8     0,2 teslas
H 0       30       45     50 kA/m

Le champ magnétique H et, par conséquent, la FMM développée par un aimant dépendent donc de la densité de flux B.

Connaissant les dimensions de l'aimant, on peut calculer la FMM et le flux qu'il produit. Le flux est donnée par:

θ = B x (section de l'aimant)

et la FMM est:

FMM = Hx (longueur de l'aimant)

Exemple 15-3 Un aimant permanent en alnico V possède les dimensions données à la Fig. 15-8.

Figure 15-8 Voir exemple 15-3

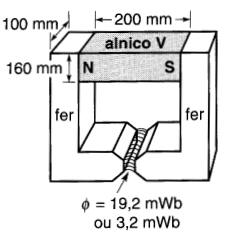
Les pièces polaires ajoutées aux extrémités de l'aimant sont en fer doux, et servent a canaliser le flux vers l'entrefer. On suppose que la longueur de l'entrefer est variable, ce qui permet de faire varier le flux θ.

Calculons la FMM développée par l'aimant lorsque le flux vaut (a) 19,2 mWh et (h) 3.2 mWb.

Solution

La section de l'aimant est:

A = 100 mm x 160 mm = 16 000 mm² = 0,016 m²

a) Pour un flux de 19,2 mWb, la densité de flux dans l'aimant est:

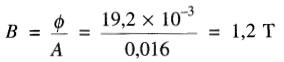
La courbe de désaimantation (Fig. 15-7) indique que le champ magnétique développé par l'aimant dans ces circonstances est de 15 kA/m.

Comme la longueur de l'aimant est de 200 mm, il produit une FMM de :

FMM = Hl = 15 000 x 200 / 1000 = 3000 A

L'aimant agit donc comme une bobine qui développe une FMM de 3000 ampères-tours.

b) Lorsqu'on augmente l'entrefer de façon que le flux tombe à 3,2 mWb, la densité de flux devient:

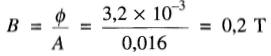
À cette densité, la valeur de H développée par l'aimant est de 50 kA/m (Fig. 15-7). Il s'ensuit que la FMM créée par l'aimant est:

FMM = Hl = 50 000 x 200 / 1000 = 10 000 A

L' aimant agit maintenant comme une bobine qui développe une FMM de 10 000 A.

Cet exemple montre bien que la FMM développée par un aimant dépend de la densité de flux qui le traverse. Plus la densité est grande, plus la FMM est faible.

L'aimant se comporte exactement comme un électro-aimant, sauf que sa FMM ne demeure pas fixe.

Produit énergétique

Dans la plupart des montages comportant un aimant permanent, on désire produire un flux θ dans un entrefer dont la longueur et la section sont connues.

On peut donc calculer la FMM requise pour l'entrefer et, par conséquent, celle que l'aimant permanent doit produire. Comme la valeur de H n'est pas constante, mais varie avec B, on doit se demander quelle valeur on doit choisir.

En pratique, on choisit le point de la courbe de désaimantation où le produit BH est maximal. On peut prouver en effet que ce choix assure une quantité minimale de matériau magnétique. Le produit BH en un point correspond à la superficie du rectangle formé à ce point, comme l'indique la Fig. 15-9.

Figure 15-9 Le matériau magnétique produit son énergie magnétique maximale au point Bd Hd, où le produit BH est maximal

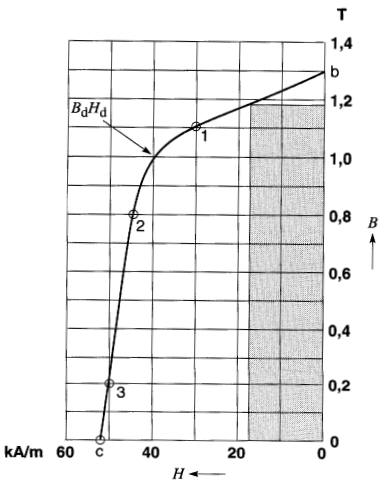
À mesure que l'on se déplace sur la courbe bc, il est évident qu'il existe un point unique (Bd Hd) où le rectangle aura une superficie maximale. Le produit Bd Hd s'appelle produit énergétique du matériau. Dans le cas de l'alnico V, ce point correspond

à Bd = 1T, Hd = 40 kA/m. Le produit énergétique de ce matériau est donc:

Wd = Bd Hd = 1T x 40 kA/m = 40 kJ/m³

Dans le cas de l'Indox®, le point optimal correspond à Bd = 0,2T, Hd = 100 kA/m. Le produit énergétique est donc :

Wd = Bd Hd = 0,2T x 100 kA/m = 20 kJ/m³

Tout matériau magnétique possède ainsi une valeur de Hd et une valeur de Bd optimales assurant la meilleure utilisation du matériau magnétique.

On juge la qualité d'un matériau à aimant permanent à la valeur maximale de son produit énergétique. Pour un champ donné, plus ce produit est grand, plus l'aimant sera petit.

Ainsi, l' alnico V a un produit énergétique Bd Hd = 40 kJ/m³ tandis que l'acier au carbone, utilisé couramment dans les aimants permanents avant 1935, a un Bd Hd de 1,2 kJ/m³ seulement.

Par conséquent, pour produire un flux quelconque dans un circuit magnétique donné, un aimant permanent en alnico V est 40/1,2 = 33 fois plus petit qu'un autre en acier au carbone.

Les aimants permanents encore plus puissants composés de néodyme-boron-fer atteignent des produits énergétiques de l'ordre de 380 kJ/m3. Enfin, il n'est pas difficile de comprendre pourquoi l'acier au silicium n'est jamais employé comme aimant permanent; son produit énergétique BdHd n'est que de 0,005 kJ/m3.

Calcul d'un aimant permanent

Les principes que nous venons d'étudier permettent de faire le calcul élémentaire d'un aimant permanent.

En voici un exemple.

Exemple 15-4

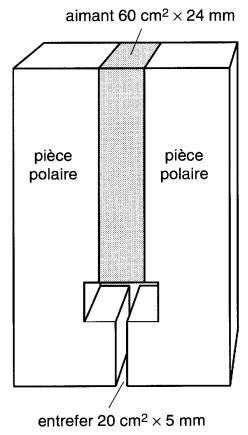
Calculer les dimensions d'un aimant en ferrite du type Indox 5 permettant de produire une densité de flux de 0.6T dans un entrefer ayant une surface A = 20 cm² et une longueur de 5 mm.

On sait que B_d = 0,2T et Hd = 100.kA/m

Solution

Calculons d'abord le flux dans l'entrefer:

θ = BA = 0,6 x 20 x 10^-4 = 0,0012 Wb

Ce flux θ traverse également l'aimant; la densité optimale Bd étant de 0,2 T, il faut que la section de l'aimant soit:

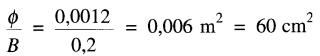
La FMM requise pour l'entrefer est donnée par la formule 14-9:

FMM = 800 000 Bl = 800 000 x 0,6 x 0,005 = 2400A

Pour l'Indox , Hd = 100 kA/m, d'où la longueur la de l'aimant est:

Ia = FMM / Hd = 2400 / 100 000 = 0,024 = 24 mm

Pour conduire le flux et pour le concentrer dans l'entrefer afin d'y créer une densité 3 fois plus élevée que dans l'aimant lui-même, on doit avoir recours à deux pièces polaires en fer doux. La densité accrue dans l'entrefer est obtenue en diminuant la section des pôles vis-à-vis de l'entrefer.

L'arrangement est montré à la Fig. 15-10.

Figure 15-10 Calcul d'un aimant permanent (exemple 15-4)

Variation du champ avec le temps et la température - point de Curie

Les champs magnétiques créés par les aimants permanents modernes sont très stables. Bien que tout aimant ait tendance à perdre sa force avec le temps, cette diminution est si lente qu'elle est presque imperceptible.

Par exemple, on estime qu'un aimant en almico V retient 99 % de son aimantation originale après 100 ans d'utilisation. On peut, par des méthodes spéciales. stabiliser l'aimant encore davantage. La température joue également un rôle important.

À mesure qu'elle augmente, la densité de flux produite par l'aimant diminue et, à une température élevée, appelée point de Curie, il perd complètement sa perméabilité de même que ses propriétés d'aimant permanent.

Cette haute température provoque en effet une vibration atomique intense qui détruit l'orientation des domaines. Le point de Curie varie avec les matériaux, mais il se situe habituellement entre 700 °C et 900 °C .

Aimantion et désaimantation d'un aimant permanent

Pour aimanter un aimant permanent, on doit le placer dans un champ suffisamment fort afin d'orienter tous les domaines dans le même sens. Cela requiert une FMM extrêmement intense, mais comme les domaines s'orientent presque instantanément, celle-ci peut être appliqué pendant une fraction de seconde seulement.

Cette courte période d'aimantation permet de faire circuler des courants énormes (jusqu'à 100 000 A) dans des conducteurs relativement petits sans excéder le I²t permis pour le conducteur. Par exemple, dans la Fig . 15-11, un conducteur portant un courant momentané de 50 000 A crée la FMM requise.

Figure 15-11 Aimantation d'un aimant permanent par un courant momentané de forte intensité

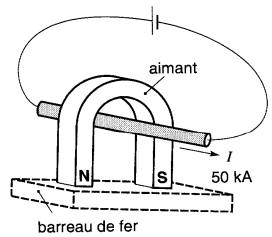
La boucle formée par le conducteur et la source cons- titue l'unique spire de la «bobine». Le circuit magnétique de l'aimant est complété par un barreau de fer doux afin que le champ intense H soit appliqué directement sur l'aimant.

Si le barreau n'était pas utilisé, une partie de la FMM créée par le conducteur serait «consommée» inutilement par l'entrefer entre les deux pôles N,S. Pour désaimanter un aimant permanent, on doit le placer dans un champ alternatif intense et réduire graduellement la valeur de ce champ jusqu'à zéro.

On peut encore employer une seule spire portant un courant alternatif très intense et décroissant.

Conversion de l'énergie mécanique en énergie magnétique

Lorsque les pôles nord et sud d'un aimant permanent sont réunis par une armature en fer doux, l'énergie magnétique contenue dans l'aimant et dans l'armature sont toutes deux très faibles (Fig . 15-12). Cependant, quand on éloigne l'armature, l'énergie magnétique dans l'entrefer ainsi créée peut être considérable (Fig . 15- 13).

Figure 15-12 Une armature en fer doux collée aux pôles d'un aimant permanent emmagasine peu d'énergie magnétique

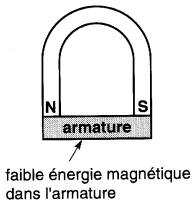
Figure 15-13 Lorsque l'armature est retirée, le champ dans l'air emmagasine une énergie considérable. Cette énergie provient du travail mécanique exercé en retirant l'armature

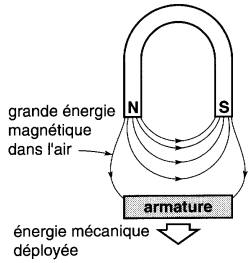
En effet, pour séparer l'armature de l'aimant, on doit dépenser un certain travail. Cette énergie mécanique est transformée et emmagasinée dans le champ magnétique de l'entrefer.

Il y a donc conversion directe de l'énergie mécanique en énergie magnétique lorsqu'on éloigne une armature des pôles d'un aimant.

D'autre part, en rapprochant l'armature, on doit lutter contre la force d'attraction exercée par l'aimant. Il s'ensuit que l'énergie magnétique libérée par le champ à mesure que le volume de l'entrefer diminue se trouve maintenant convertie en énergie mécanique dépensée lors du freinage.

Lorsque l'armature est de nouveau collée contre les pôles, l'énergie magnétique contenue dans l'air redevient nulle.

Durant ce processus, l'énergie magnétique dans l'aimant et dans l'armature de- meure en tout temps négligeable. L'énergie mécanique est donc convertie en énergie magnétique lorsqu'on éloigne l'armature, et cette énergie magnétique est reconvertie en énergie mécanique lorsqu'on rapproche l'armature.

On comprend alors pourquoi l'aimant ne perd pas sa force même si l'on répète ce processus des centaines de fois.

On peut aussi se demander pourquoi l'aimant d'un ra- masse-clous ne perd pas de sa force, même après avoir ramassé des milliers de clous dont chacun demeure un peu aimanté après avoir été attiré par l'aimant. L'explication vient du fait que l'énergie magnétique associée à chaque clou aimanté provient de l'énergie mécanique qu'on a dû déployer pour le séparer de l'aimant.

Cycle d'hystérésis

Les transformateurs et la plupart des moteurs électriques fonctionnent à courant alternatif de sorte que le flux circulant dans leurs parties en acier change continuellement de valeur et de sens. Les domaines doivent donc s'orienter tantôt dans un sens, tantôt dans l'autre à un rythme qui est d'autant plus rapide que la fréquence du réseau est élevée.

Ainsi, sur un réseau à 60 Hz, les domaines décrivent un cycle complet en 1/60e de seconde, passant par des densités maximales +B_m et -B_m sous l'effet d'un champ magnétique va- riant de +H_m à -H_m.

Si l'on trace les variations de la densité de flux B (en teslas) en fonction du champ magnétique H(en A/m), on obtient une courbe fermée portant le nom de cycle d'hystérésis (Fig. 15-14). Le cycle suit la séquence a,b,c,d,e,f,a, à raison de 60 fois par seconde.

Figure 15-14 Cycle d'hystérésis d'un matériau magnétique. L'énergie dissipée par cycle est proportionnelle à la surface a b c d e f a de la courbe.

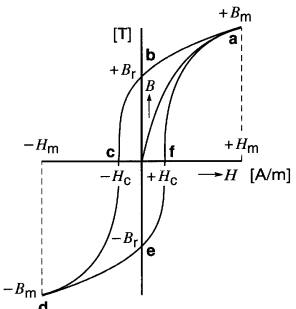
Sur ce cycle, on reconnaît les valeurs de la densité de flux rémanent Br et du champ coercitif H, comme dans le cas des aimants permanents.

Pertes par hystérésis

À chaque cycle complet d'hystérésis, il se produit une perte d'énergie. La perte est due au «frottement» des domaines magnétiques lorsqu'ils changent de sens . La quantité d'énergie dissipée par mètre cube est égale à la surface du cycle d'hystérésis.

Considérons, par exemple, le cas simplifié du cycle d' hystérésis rectangulaire de la Fig. 15-15.

Figure 15-15 Calcul de l'énergie dissipée par hystérésis

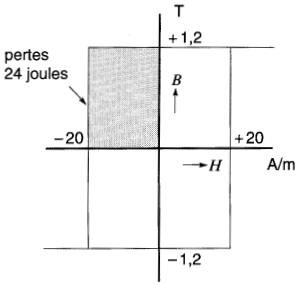
L'énergie requise par mètre cube de ce matériau vaut:

W = 1,2T x 20A/m x 4 = 96 T A/m, soit 96 J/m³

Si la fréquence du réseau est de 60 Hz, on dépensera, par mètre cube, une puissance de:

P = 96 J x 60 cycles/seconde = 5760 J/s = 5760 W

Cette puissance est dissipée sous forme de chaleur dans l'acier, ce qui provoque une augmentation de sa température. Pour réduire ces pertes, on a donc intérêt à réduire la surface du cycle d'hystérésis des matériaux destinés à supporter des flux alternatifs.

Par exemple, an utilise l'acier à grain orienté pour les noyaux de transformateurs. Les courbes de la Fig. 15-16a permettent de comparer les cycles d'hystérésis de l'alnico V et de l'acier Silectron utilisé dans la fabrication des transformateurs.

Figure 15-16a Comparaison du cycle d'hystérésis de l'alnico V avec celui d'un acier utilisé dans les transformateurs

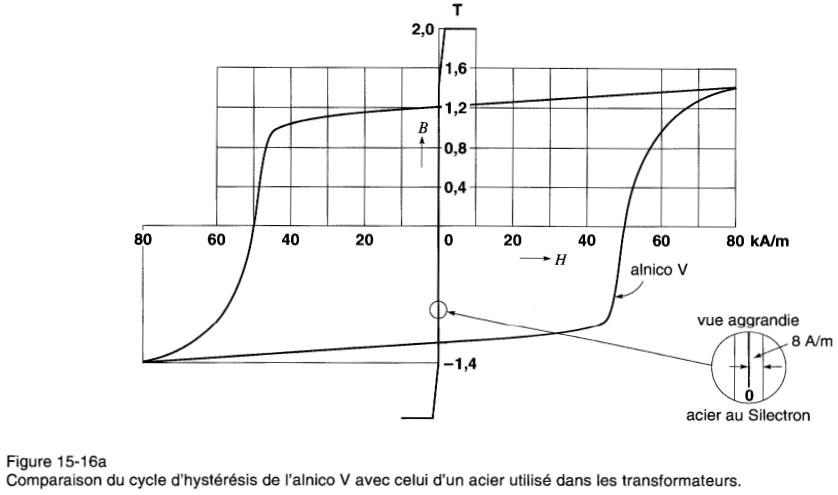
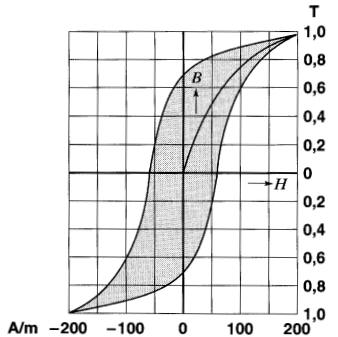
On constate que la surface du cycle de l' alnico V est environ 5000 fois plus grande que celle du Silectron. L'alnico ne convient donc absolument pas pour conduire les flux alternatifs. Le cycle d'hystérésis d'un acier utilisé dans les relais à courant alternatif est donné à la Fig. 15-16b.

Figure 15-16b Cycle d'hystérésis d'un acier pour relais à courant alternatif

Pertes par hystérésis dues à la rotation

Remarquons que des pertes par hystérésis seront également produites dans une pièce de fer tournant dans un champ constant et fixe.

Ainsi, les pôles nord des domaines dans la barre de la Fig. 15-17a sont initialement dirigés vers l'extrémité B.

Figure 15-17 Pertes par hystérésis dues à la rotation

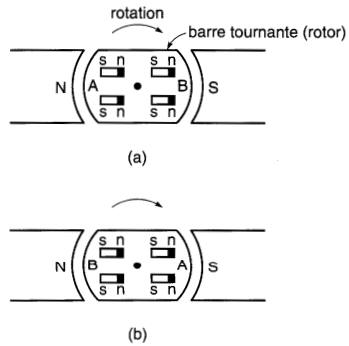
Quand la barre aura fait un demi-tour (Fig. 15-17b), les pôles nord seront dirigés vers l'extrémité A. Il y a donc inversion des domaines dans la pièce, même si le sens du champ magnétique ne change pas.

Ce phénomène se produit dans les machines à courant continu où l'induit tourne dans un champ fixe. Ces pertes par hystérésis provoquent un échauffement de l'induit. L'échauffement peut être considérablement réduit par l'emploi d'un acier de bonne qualité.

Exemple 15-5

Le rotor d'un moteur à courant continu tourne a 7200 r/min entre deux pôles magnétiques produisant une densité de flux maximale de 0.8 tesla. Le rotor a un volume de 0,2 m³ et la surface du cycle d' hystérésis est de 15 T.A/m.

 Calculer les pertes par hystérésis.

Solution

Puisque l'énergie dépensée par cycle est de 15 T.A/m = 15 J/m³, l'énergie pour un volume de 0,2 m³ vaut:

W = 15 x 0,2 = 3 joules

Puisque le rotor tourne à une vitesse de 7200/60 = 120 r/s, on dépense 3 x 120 = 360 J/s, soit une perte dissipée en chaleur de 360 W.

Résumé

Nous avons vu dans ce chapitre que le phénomène d'hystérésis, une propriété liée aux domaines magnétiques et commune à tous les matériaux magné- tiques, permet de créer les aimants permanents.

Tout comme une bobine parcourue par un courant, un aimant possède une force magnétomotrice qui pro- duit un flux magnétique entre ses pôles.

Nous avons vu qu'une énergie magnétique est emmagasinée dans l'espace entourant un aimant . Un aimant exerce sur un autre matériau magnétique (comme un morceau de fer) une force d'attraction dirigée selon les lignes de force du champ.

Lors du travail effectué pour séparer le morceau attiré, il y a conversion de l'énergie mécanique en énergie magnétique, laquelle est emmagasinée dans le champ.

De même, lors du rapprochement, l'énergie magnétique dans le champ est reconvertie en énergie mécanique. Un aimant permanent se distingue des autres matériaux magnétiques par la grande surface de sa courbe de désaimantation B-H.

La surface comprise sous cette courbe est une mesure de l'énergie requise pour désaimanter l'aimant. Cette courbe passe par trois points caractéristiques de l'aimant : sa densité de flux rémanent Br , son champ coercitif H, et le point où le produit énergétique B-H est maximal.

Les aimants permanents modernes ont des pro- duits énergétiques élevés . Nous avons vu aussi comment calculer les dimensions d'un aimant devant produire une densité de flux donnée.

Enfin, le phénomène d'hystérésis n'a pas que des avantages. Il est la cause des pertes dans les parties en fer des machines électriques qui sont soumises à un champ magnétique variable .

À chaque fois que l'on décrit un cycle d'hystérésis, une énergie correspondant à la surface du cycle est dissipée en chaleur dans le matériau magnétique.

PROBLÈMES

Niveau pratique

15-1 Expliquer les termes suivants : induction rémanente, champ coercitif, hystérésis, point de Curie.

15-2 En se référant à la Fig. 15-6, quel est le champ magnétique développé par l'Indox, lorsque la densité de flux est 0,3 T ; 0,2 T; 0 T?

15-3 L'acier au carbone (Fig. 15-6) n'est pas un bon matériau pour aimant permanent. Expliquer.

15-4 Comment peut-on désaimanter un aimant permanent?

Niveau intermédiaire

15-5 Un aimant permanent, fait en acier au carbone, a une longueur de 0,3 m. Sachant qu'il crée un champ magnétique de 2000 A/m à une densité de flux de 0,5 T, calculer sa FMM.

15-6 Expliquer comment un aimant permanent réalise la conversion d'énergie mécanique en énergie magnétique.

15-7 Quelle est l'énergie emmagasinée dans l'entrefer de la Fig. 14-16 (section Circuits magnétiques) dont la section est de 10 cm x 12 cm?

15-8 Un morceau d' alnico V possède une longueur de 10 cm et une section de 6 cm². Quelle énergie est nécessaire pour le désaimanter complètement? Qu'arrive-t-il de cette énergie?

15-9 Si l'on introduit un morceau de fer doux dans l'entrefer de la Fig. 15-8, l'énergie dans le champ diminue. Par ailleurs, l'énergie reprend sa valeur originale lorsqu'on retire le morceau de fer. Expliquer.

Figure 15-18 Voir problème 15-11

15-10 L'Indox® a une densité de flux Bd optimale de 0,2 T. Comment peut-on créer une densité de flux de 1,2 T dans un entrefer en utilisant ce matériau?

Niveau avancé

15-11 On applique une tension alternative de 60 Hz mat bornes de l'enroulement de la Fig. 15-18, et l'on constate que le flux atteint périodiquement une valeur crête de 1,0 T.

Le noyau en acier au silicium est remplacé par un autre en acier pour relais et qui possède le cycle d'hystérésis montré à la Fig. 15-16b. Calculer la paissance approximative dissipée par hystérésis, en watt.

15-12 L'aimant permanent de la Fig. 14-14 produit un champ dans l'air dont la densité varie de point en point. La densité de flux dans une région à côté de l'entrefer est de 0,5 T. Calculer l'énergie par mm³ à cet endroit.

15-13 L' aimant permanent N Sen alnico V de la Fig. 17-12 (section Tension induite dans un conducteur) a une longueur de 200 mm et une section de 25 cm².

Si la longueur de chaque entrefer est de 3,4 mm, déterminer:

a) la densité de flux dans l'entrefer et le flux par pôle

b) la FMM développée par l'aimant.

15-14 Le pôle nord d'un aimant permanent en alnico V crée une densité de flux de 0,4 T dans un entrefer dont la longueur est de 4 mm.

a) Sachant que la surface du pôle est de 500 cm², calculer la section de l'aimant permanent afin d'utiliser le minimum de matériau magnétique

b) Calculer la FMM que l'aimant doit développer

c) Quel est le volume de l'aimant?

15-15 Le morceau de fer placé entre les pôles N, S de la Fig. 15-2 est traversé par un flux de 1,2 mWb. Les faces traversées ont des surfaces respectives de 100 cm² et de 50 cm².

a) Calculer la valeur des forces FI et F2

b) Vers quel pôle le morceau de fer est-il attiré?

Réponses

2) 0 kA/m; 100 kA/m; 200 kA/m; 5) 600 A; 7) 7,2 J;
8) 52 000 T.A/m; 3,1 J; 11) 216 W; 12) 0,1 mJ/mm³;
13a) 1,1 T; 2,75 mWb; 13b) 6000 A; 14a) 200 cm²; 14b) 1280 A;
14c) 640 cm³; 15a) 57,6 N; 115,2 N; 15b) sud