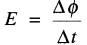Induction électromagnétique

Électrotechnique

PRINCIPE IV DE L'ÉLECTROMAGNÉTISME

Ce quatrième principe de l'électromagnétisme est à la base du fonctionnement d'un grand nombre d'appareils électriques, notamment des transformateurs et des moteurs à courant alternatif. Comme nous l'avons déjà mentionné à la section Tension induite dans un conducteur, ce phénomène fut découvert par Michael Faraday en 1831.Il est connu sous le nom de loi de l'induction électromagnétique.

Loi de l'induction électromagnétique

Cette loi énonce que:

a) si le flux à l'intérieur d'une boucle (ou spire) varie avec le temps, une tension est induite entre ses bornes;

b) la valeur de cette tension induite est proportionnelle au taux de variation du flux.Par définition, dans le SI, lorsque le flux à l'intérieur d'une boucle varie à un taux de 1 weber par seconde, une tension de 1 volt est induite entre ses bornes.

On obtient donc l'équation suivante:

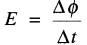18-1

où

E = tension induite, en volts [V]

Δθ = variation du flux à l'intérieur de la boucle, en webers [Wb]

Δt = intervalle de temps, en secondes [s]

Pour mieux comprendre la généralité de la loi de l'induction, imaginons une spire souple en mouvement. connectée à un circuit C quelconque. Le circuit contient des sources de tension et des résistances, et la spire porte un courant I (Fig.18-1).

Figure 18-1 La loi de l'induction de Faraday permet de calculer la tension E induite dans une spire, même dans des conditions hautement variables.

   

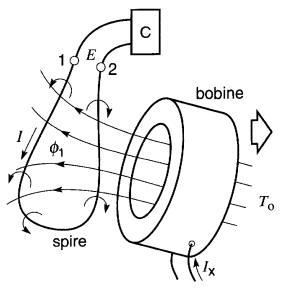
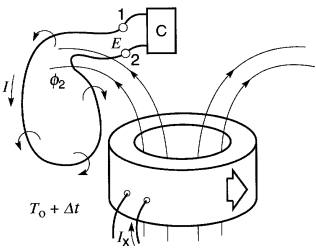
En même temps qu'elle produit son propre champ magnétique, en raison du courant I, la spire est soumise à un champ magnétique extérieur créé par une bobine qui se déplace aléatoirement vers la droite.

Quelle est la tension E induite entre les bornes 1 et 2 de la spire pendant un intervalle de temps Δt?

On pourrait difficilement imaginer un montage plus compliqué mais, d'après la loi de Faraday, il suffit de connaître les flux 01 et 02 entourés par la spire au début et à la fin de l'intervalle Δt.

La tension moyenne induite est alors donnée par la formule simple :

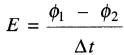
La tension induite est donc égale au changement de flux Δθ = (θ1 - θ2) divisé par le temps Δt.

On n'est plus obligé d'imaginer une «coupure» des lignes pour expliquer la tension induite, comme on l'a fait lors de l'étude du principe III, étudié à la section Tension induite dans un conducteur,.

La tension induite dans une spire est simplement due à la variation du nombre de lignes de force traversant cette spire. Le principe III apparaît donc maintenant comme un cas particulier du principe IV.

La loi de l'induction électromagnétique de Faraday ouvre la porte à un grand nombre d'applications pratiques comme l'illustrent les exemples suivants.1

Application 1 - Induction dans une bobine

Soit une bobine de N spires traversée par un flux θ IFïg.l8-2).

Figure 18-2 Si le flux o varie d'une quantité Δθ durant un intervalle Δt, la tension induite est donnée par E = NΔθ /Δt.

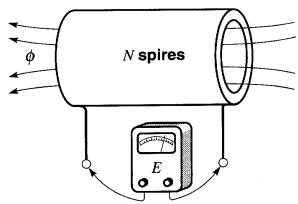
Si le flux varie d'une quantité Δθ pendant un intervalle de temps Δt, la valeur de la tension induite dans chaque spire est Δθ /Δt volts. Pour N spires, la tension E est donc N fois plus grande, soit:

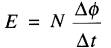    (18-2)

En augmentant le nombre de spires on réussit à augmenter la tension induite.

Exemple 18-1

Une bobine comprenant 2000 spires est traversée par un flux de 5 mWb provenant d'un aimant permanent (Fig. 18-3).

Figure 18-3 Voir exemple 18-1

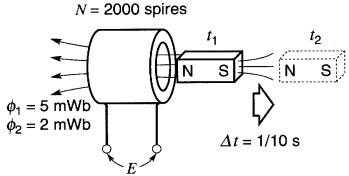
L'aimant est alors éloigné de la bobine en 1/10 de seconde et le flux à l'intérieur de la bobine baisse à 2 mWb. Quelle est la valeur moyenne de la tension induite?

Solution

La variation de flux est:

Δθ = (5 mWb - 2 mWb) = 3 mWb

Comme cette variation dure 1/10 de seconde (Δt), la valeur moyenne de la tension induite est:

E = NΔθ /Δt = 2000 x (0,003 / 1/10) = 60V

Application 2 - Tension induite dans un cadre

Lorsqu'un cadre tourne entre les pôles d'un aimant, le flux à l'intérieur du cadre varie continuellement, induisant ainsi une tension.

Par exemple, dans la Fig. 18-4a, à l'instant t = 0, le cadre n'est traversé par aucun flux, mais 20 millisecondes plus tard (Fig. 18-4b), après avoir exécuté 1/4 de tour, il est traversé par un flux de 0.01 Wb.

Figure 18-4 Loi de Faraday appliquée à un cadre tournant: a le flux à l'intérieur du cadre est nul ; b le flux à l'intérieur du cadre est de 10 mWb

 

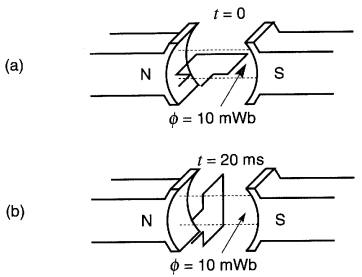
La tension moyenne induite vaut donc :

E = Δθ /Δt = 0,01 / 0,02 = 0,5 V

On aurait trouvé la même tension moyenne en appliqua t la formule E = Blv du principe III de l'électromagnétisme. Cependant, pour calculer la tension par serte méthode, il faudrait connaître les dimensions du cadre et la valeur de la densité de flux B.

Application 3 - Induction mutuelle

La variation du courant dans une bobine peut induire une tension dans une autre bobine. Soient deux bobines A et B enroulées sur le même noyau d'acier (Fig. 18-5).

La bobine A peut être raccordée à une batterie de piles au moyen d'un interrupteur.

À la Fig. 18-5a, le flux dans le noyau est nul car l'interrupteur est ouvert.

Figure 18-5 Induction mutuelle:

a. le montage à l'état de repos ;

b. la fermeture de l'interrupteur provoque la circulation d'un courant. La croissance du flux induit une tension Et dans la deuxième bobine;

c. si l'interrupteur est ouvert brusquement, la décroissance rapide de 0 induit une haute tension E2

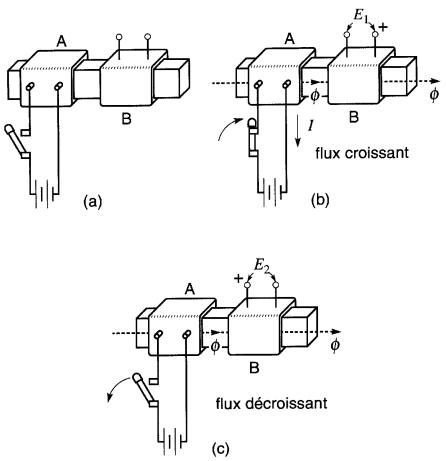
Dès que l'interrupteur est fermé (Fig. 18-5b), un courant commence à circuler dans la bobine A produisant des lignes de flux dans le sens indiqué.

Le flux dans le noyau passe alors de la valeur zéro à une valeur 0; il y a donc variation du nombre de lignes de flux traversant la bobine B.

D'après la loi de l'induction, une tension est induite dans cette bobine. Cette induction d'une tension dans une bobine par la variation du courant dans une autre bobine porte le nom d'induction mutuelle.

Il est donc possible, par couplage magnétique seulement, de transmettre de l'énergie électrique d'une bobine à une autre.

C'est sur ce principe ue fonctionnent les transformateurs.

On peut remarquer que l'ouverture rapide de l'interrupteur produit une variation rapide du flux ; il en résulte une tension induite E2 très élevée (voir Fig. 18-5c).

Ce principe est mis à profit dans la bobine d'induction reliée aux bougies d'allumage d'une automobile. La tension produit une étincelle qui amorce l'explosion d'un mélange d'essence et d'air.

Application 4 - Générateur à réluctance variable

Un aimant permanent N-S produit un flux dans un circuit magnétique formé d'un noyau stationnaire et d'un rotor en fer doux (Fig. 18-6).

Figure 18-6 Générateur à réluctance variable

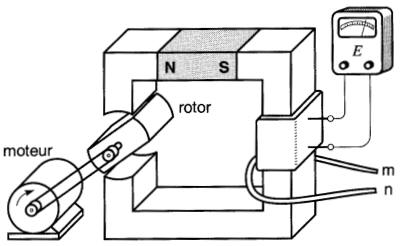
La valeur du flux dépend de la réluctance du circuit magnétique, donc de la position du rotor. Lorsque celui-ci se trouve dans l'axe du noyau, l'entrefer est court et le flux possède alors sa valeur maximale θ1; mais si on le fait tourner de 90°, l'entrefer augmente et le flux tombe à sa valeur minimale θ2.

Si l'on entraîne le rotor par un moteur quelconque, le flux varie de façon périodique entre ses valeurs extrêmes θ1 et θ2 (Fig. 18-7).

Figure 18-7 Variation du flux dans le noyau, entre les valeurs extrêmes θ1 et θ2. La tension induite est maximale lorsque le flux varie rapidement (instants t3 et t4); elle est nulle lorsque le taux de changement est zéro (instants t1 et t2)

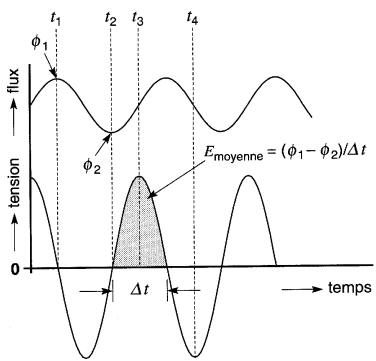
Cette variation périodique induit une tension alternative dans la bobine qui subsiste aussi longtemps que le rotor tourne. La valeur moyenne de la tension induite pendant 1/4 de tour vaut E = (θ1 - θ2)/Δt volts, Δt étant le temps pris pour exécuter cette fraction de tour.

Champ magnétique et champ électrique

Faraday a découvert le phénomène de l'induction d'une tension, mais c'est l'illustre physicien et mathématicien anglais James Clerk Maxwell qui a expliqué la raison fondamentale de sa création.

D'après Maxwell, un champ électrique s'établit autour de tout champ magnétique qui varie avec le temps. Les lignes de force de ce champ électrique sont représentées par une série de boucles fermées encerclant les lignes du flux «inducteur» (Fig. 18-8a et 18-8b). Le concept de champ électrique est présenté à la section Phénomènes électrostatiques.

Figure 18-8 Un champ magnétique qui varie produit un champ électrique. Si des électrons sont présents dans le voisinage du champ magnétique, le champ électrique créé exerce sur ceux-ci une force de sens opposé à celui des lignes de champ électrique.

a. sens du champ électrique lorsque le flux croît;
b. sens du champ électrique lorsque le flux décroît
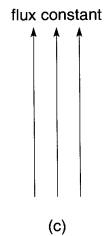
c. le champ électrique est absent lorsque le flux ne varie pas

       

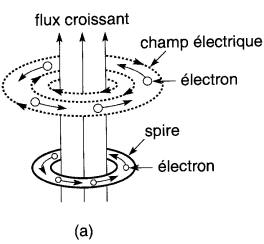
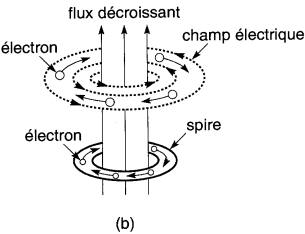
Si le flux croît, le sens des lignes électriques est comme indiqué à la Fig. 18-8a; s'il décroît, elles changent de sens (Fig. 18-8b).

 Enfin, si le flux reste constant, c'est-à-dire qu'il ne varie pas en fonction du temps, le champ électrique disparaît (Fig. 18-8c).

Ce champ électrique possède les mêmes propriétés que celui existant entre les bornes d'une pile, de sorte qu'un électron placé dans ce champ subira une force l'obligeant à suivre le trajet circulaire des lignes de champ électrique.

L'électron se mettra à tourner autour du champ magnétique, sa vitesse augmentant rapidement à chaque tour. Remarquer que c'est la croissance ou la décroissance du champ magnétique qui détermine le sens de rotation de l'électron.

De même, si l'on place une spire conductrice fermée autour d'un champ magnétique variable, les électrons libres qu'elle contient se déplacent, créant ainsi un courant électrique dans la spire.

Comme dans tout conducteur, la vitesse de déplacement des électrons est beaucoup plus faible que dans le cas précédent à cause de la structure atomique de la spire. Ce courant électronique subsiste aussi longtemps que le champ magnétique varie.

On se souvient que la circulation des électrons correspond à un courant dont le sens conventionnel est l'inverse du courant électronique.

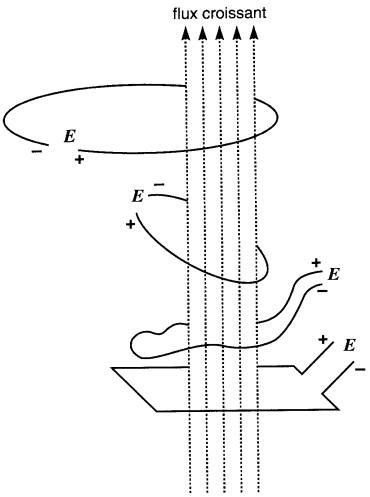
Si le flux varie à l'intérieur d'une spire ouverte, les électrons mis en circulation s'accumulent sur l'une de ses deux extrémités; il en résulte une différence de potentiel E comme Faraday l'avait constaté. Cette différence de potentiel, ou tension, reste la même quelle que soit la forme de la spire, pourvu qu'elle entoure le même flux (Fig. 18-9).

Figure 18-9 La tension induite E est rigoureusement identique pour les quatre spires entourant un même flux, quelles que soient leur forme et leur orientation

Polarité de la tension induite - Loi de Lenz

La polarité de la tension induite dépend exclusivement de la façon dont le flux varie à l'intérieur de la spire. Alors que la loi de Faraday permet de trouver la valeur de la tension induite, la loi de Lenz permet d'en déterminer sa polarité. 

Loi de Lenz

Soit un flux inducteur θ1 dont la variation induit une tension E dans une bobine. La polarité de la tension induite E est telle qu'elle tend à faire circuler dans la bobine un courant I2, créant un flux θ2 qui s'oppose à la variation du flux θ1.

On peut éclaircir l'énoncé de la loi de Lenz à l'aide de la Fig. 18-10.

Figure 18-10 Schémas montrant l'application de la loi de Lenz pour déterminer la polarité d'une tension induite.

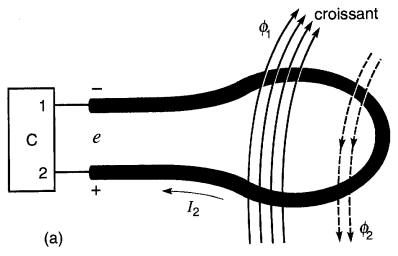
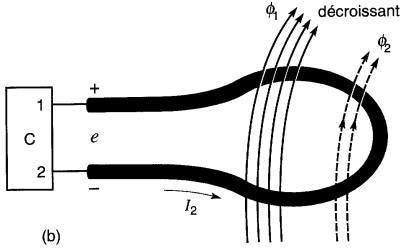
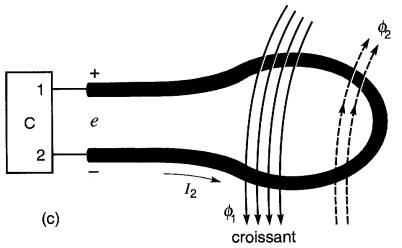
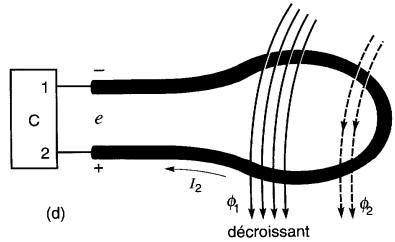
fig. 18-10a : Le flux total θ1 entouré par la spire se dirige dans le sens indiqué et il est croissant. Le système cherche à s'opposer à cette croissance.

Pour ce faire, on imagine un courant I2 qui circule dans la spire afin de produire un flux θ2 s'opposant à la croissance de θ1. Le flux θ2 doit donc avoir un sens opposé à celui de θ1. En appliquant la règle de la main droite (section 13.3), il s'ensuit que I2 doit circuler dans le sens indiqué. Comme le courant se dirige vers la borne 2, celle-ci est (+) par rapport à la borne 1.

fig. 18-10b : Le flux total θ1 entouré par la spire se dirige dans le même sens que dans la Fig. 18-1a, mais il est décroissant. Le système cherche à s'opposer à cette décroissance.

Pour ce faire, on imagine un courant I2 qui circule dans la spire afin de produire un flux o, s'opposant à cette décroissance. Le flux θ2 doit donc être orienté dans le même sens que θ1. En appliquant la règle de la main droite, il s'ensuit que I2 doit circuler dans le sens indiqué. Comme le courant se dirige vers la borne 1, celle-ci est maintenant (+) par rapport à la borne 2.

Fig. 18-10c : Le flux total θ1 entouré par la spire est orienté dans le sens inverse de celui des deux figures précédentes, et il est croissant. Le système cherche encore à s'opposer à cette croissance.

Pour ce faire, on imagine un courant I2 qui circule dans la spire afin de produire un flux θ2 s'opposant à cette croissance, et créant donc un flux θ2 de sens opposé à celui de θ1. En appliquant la règle de la main droite, il s'ensuit que I2 doit circuler dans le sens indiqué. Comme le courant se dirige vers la borne 1, celle-ci est (+) par rapport à la borne 2.

Fig. 18-10d : Enfin, le flux total θ1 entouré par la spire se dirige dans le même sens que celui de la Fig. 18-10c. mais il est décroissant. Le système cherche encore à s'opposer à cette décroissance.

Pour ce faire, on imagine un courant I2 qui circule dans la spire afin de produire un flux θ2 s'opposant à cette décroissance, et créant donc un flux de même sens que θ1. En appliquant la règle de la main droite, il s'ensuit que I2 doit circuler dans le sens indiqué. Comme le courant se dirige vers la borne 2, celle-ci est (+) par rapport à la borne 1.

Le même raisonnement permet de trouver la polarité de la tension apparaissant aux bornes d'un enroulement ou d'une bobine dans un circuit quelconque.

Elle montre une spire de résistance nulle raccordée aux bornes 1 et 2 d'un circuit C. Ce dernier pourrait contenir n'importe quelle combinaison de sources de tension et de résistances. La spire pourrait aussi porter un courant I quelconque (pas indiqué). Cette spire entoure un flux inducteur θ1 qui varie en fonction du temps.

Ce flux peut être créé par le courant qui circule dans la spire elle-même, ainsi que par un flux provenant d'un montage à l'extérieur. Selon la loi de Faraday, la valeur de la tension induite apparaissant entre les bornes 1 et 2 est donnée par l'expression

E = Δθ1/Δt

Pour déterminer sa polarité, considérons maintenant les quatre schémas de la Fig. 18-10.On examinera successivement les quatre combinaisons possibles obtenues avec un flux θ1 orienté vers le haut ou vers le bas, et dont la valeur augmente ou diminue.

Exemple 18-2

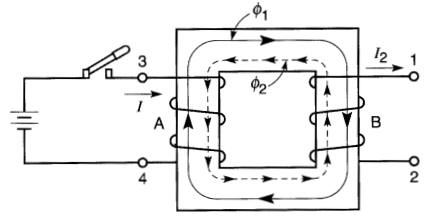
Déterminer la polarité de la tension induite entre les bornes de la bobine B (Fig 18-11) lors de la fermeture de l'interrupteur.

Figure 18-11 Voir exemple 18-2

Solution

À la fermeture de l'interrupteur, le courant dans la bobine A croît à partir de zéro jusqu'à une certaine valeur imposée par la tension de la source et la résistance de la bobine A.

Il s'établit donc un flux variable θ1 croisant dont le sens est donné par la règle de la main droite. Ce flux variable θ1 traverse également la bobine B et une tension est induite entre ses bornes 1 et 2.

Sa polarité est donnée par la loi de Lenz. La bobine B tend à produire un flux θ2 s'opposant à la croissance du flux θ1, donc circulant dans le sens opposé à celui de θ1 (Fig. 18-11).

En supposant que le flux θ1, est créé par un courant fictif I2, on découvre que la borne 1 est (+) par rapport à la borne 2. De la même façon, on note que la tension induite entre les bornes 3 et 4 est telle que 3 est (+) par rapport à 4.

Méthode de mesure du flux

La loi de Faraday nous offre une méthode facile pour mesurer un flux, comme, par exemple, celui créé par un aimant permanent. Soit une bobine possédant N spires, placée au centre d'un aimant permanent (Fig. 18-12).

Figure 18-12 Méthode de mesure du flux d'un aimant permanent.

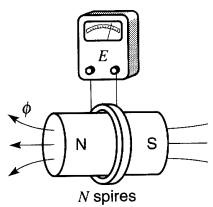
Dans cette position. La bobine entoure (ou accroche) le flux entier de l'aimant.

Si l'on retire l'aimant rapidement, le flux à l'intérieur de l'enroulement tombe vite à zéro et, pendant ce temps, une tension relativement élevée est induite aux bornes de la bobine. La tension instantanée E dépend de la distribution du flux et de la vitesse instantanée du déplacement; elle pourrait avoir l'allure montrée à la Fig. 18-13a.

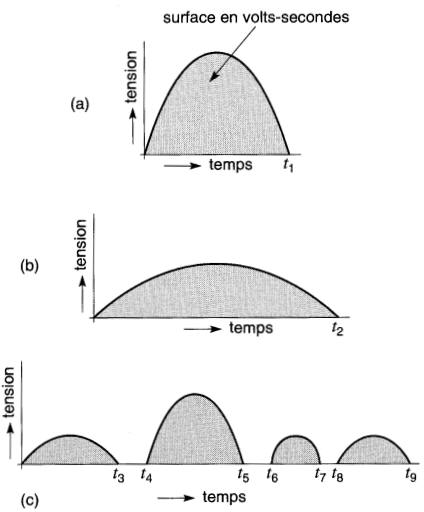
Figure 18-13

a. Si l'aimant est retiré rapidement, une tension élevée de courte durée est induite ;

b. si l'aimant est retiré lentement, une faible tension de plus longue durée est induite;

c. si l'aimant est retiré par étapes avec plusieurs arrêts, la tension induite a la forme indiquée Dans les trois cas, la surface hachurée est la même. Sa valeur en volts-secondes, divisée par le nombre de spires, donne le flux de l'aimant permanent.

Par ailleurs, si l'on retire l'aimant très lentement, une faible tension est induite pendant un temps plus long (Fig. 18-13b).

Enfin, si l'on retire l'aimant par étapes en arrêtant le déplacement à quelques reprises, on obtient une courbe de tension interrompue (Fig. 18-13e).

Si l'on mesurait les surfaces hachurées (en volts-secondes) situées en dessous de chacune de ces trois courbes, on constaterait qu'elles sont toutes les mêmes.

Le nombre de volts-secondes reste donc le même quelle que soit la manière dont on retire l'aimant. D'après la loi de Faraday, on peut prouver que le nombre de volts-secondes induits est égal au nombre de spires multiplié par le changement de flux à l'intérieur de la bobine.

C'est ce qu'exprime la relation suivante:

Volts-secondes = N(θ1 - θ2)    (18-3)

où

θ1 = flux initial dans la bobine, en webers [Wb]
θ2 = flux final dans la bobine, en webers [Wb]
N = nombre de spires

Pour mesurer ces volts-secondes, on utilise des voltmètres spéciaux, appelés voltmètres intégrateurs. Une autre méthode consiste à enregistrer l'impulsion de tension sur l'écran d'un oscilloscope. En observant l'amplitude de la tension en fonction du temps, il est facile de calculer les volts-secondes, et dès lors la valeur du flux.

Exemple 18-3

On désire mesurer le flux produit par un aimant permanent. À cette fin, on glisse une bobine de 200 spires au centre de l'aimant comme l'indique la Fig. 18-12.

Ensuite, on retire rapidement et totalement l'aimant de la bobine. Un voltmètre intégrateur enregistre une impulsion de 400 millivolts-secondes. Quelle est la valeur du flux?

Solution

Puisque l'aimant est retiré complètement de la bobine, le flux final θ2 est nul.

On aura donc:

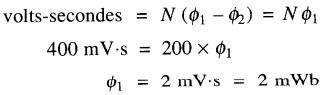
Tension appliquée et tension induite dans une bobine

Considérons une batterie de piles produisant une tension fixe E, que l'on peut brancher aux bornes d'une bobine au moyen d'un interrupteur (Fig. 18-14).

Figure 18-14 Circuit dont tout les composants ont une résistance nulle. Lorsque l'interrupteur est fermé, la tension induite EI est rigoureusement égale à la tension Es de la source.

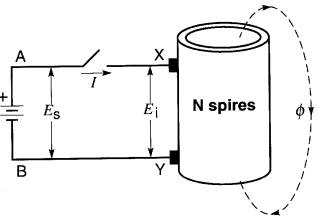
Supposons que la résistance de la bobine, ainsi que la résistance interne de la batterie soient strictement nulles. Qu'arrive-t-il à la fermeture de l'interrupteur?

Dans un premier temps, on est porté à croire que le fait de brancher une batterie sur une bobine de résistance nulle provoque un court-circuit franc et qu'un énorme courant I circule immédiatement dans le circuit. Cependant, dès qu'un courant commence à circuler, celui-ci produit un flux.

De plus, au fur et à mesure que le courant croît, le flux augmente aussi. Mais l'augmentation du flux induit, à son tour, une tension Ei aux bornes de la bobine.

Comme la résistance des conducteurs AX et BY est nulle, cette tension est nécessairement égale, en valeur et en polarité, à celle de la source.

On peut donc écrire:

Ei = Es     (18-4)

De plus, d'après l'équation 18-2:

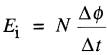
il s'ensuit que:

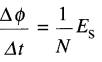    (18-5)

C'est dire que le taux de variation du flux Δθ/Δt est proportionnel à la tension Es appliquée à l'enroulement. Ce résultat est important, car il met en évidence une relation entre le flux et la tension (plutôt que le courant) appliquée à une bobine.

Si la tension Es est fixe (comme dans notre exemple) on peut écrire :

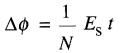    (18-6)

Δθ = changement de flux à l'intérieur de l'enroulement [Wb]
N = nombre de spires de l'enroulement
ES = tension fixe appliquée à l'enroulement [V]
t = temps d'application de la tension [s]

Exemple 18-4

L'enroulement d'un gros transformateur de 100 kV possède 2500 spires. On branche une pile de 1,5 V aux bornes de l'enroulement pendant 40 secondes. Calculer le flux dans le noyau à la fin de cette période, sachant que le flux initial est nul.

Solution

En utilisant l'équation 18-6, on trouve:

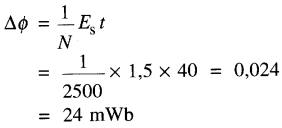
Cet exemple montre que le changement de flux à l'intérieur d'un enroulement dépend de la tension qu'on lui applique et de la durée de son application.

La valeur du courant d'excitation I qui en découle dépend des propriétés du circuit magnétique. Cette constatation est importante parce qu'on est souvent porté à croire que c'est le courant I et non la tension Es qui produit le changement de flux.

Exemple 18-5

Dans la Fig. 18-14, E, = 6 V, N = 4000 spires, et un courant de 1 A produit un flux de 2 mWh. Le flux proportionnel au courant 1. La résistance de la bobine est négligeable.

Calculer:

a)la valeur du flux et (lu courant 4 secondes après la fermeture de l'interrupteur

b) la valeur du flux et du courant 36 secondes après la fermeture de l'interrupteur

Solution

a) Le flux après 4 secondes est donné par

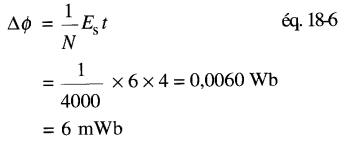
Étant donné qu'un courant de 1 A produit 2 mWb, il s'ensuit qu'il faut un courant de 3 A pour produire 6 mWb.

b) Après une période de 36 secondes, le flux sera 36/4 = 9 fois plus grand qu'après 4 secondes ; par conséquent, le flux à ce moment sera 6 mWb x 9 = 54 mWb.

Le courant correspondant est 9 X 3A = 27A. On constate que le flux et le courant augmentent tous deux linéairement avec le temps.

Si la résistance du montage demeurait strictement nulle, le courant augmenterait théoriquement sans limite.

Exemple 18-6

Il arrive parfois que des perturbations à la surface du soleil produisent des courants intenses clans la stratosphère. Ces courants produisent à leur tour un champ magnétique variable qui induit une tension de quelques dizaines de volts à la surface de la terre.

Ce phénomène. qu'on appelle orage géomagnétique, produit ainsi une tension induite qui porte le nom de tension tellurique. La tension varie très lentement et peut durer pendant quelques minutes avant de changer de polarité. De plus, elle s'étend sur des centaines de kilomètres.

Considérons un long réseau de transport à 735 kV, soumis à un orage géomagnétique. Les lignes sont raccordées au sol à travers les bobinages des transformateurs situés dans les postes séparés de centaines de kilomètres.

La différence de potentiel tellurique induite dans l'immense boucle formée par la ligne, les transformateurs et la terre peut, dans ces conditions. provoquer la saturation de certains transformateurs.

Supposons qu'ils deviennent saturés lorsque le flux atteint le seuil de 950 mWh. Les enroulements en jeu possèdent 2000 spires.

Si le flux initial est de 800 mWb, calculer le temps requis pour atteindre le point de saturation, lorsque la tension tellurique effective est de 15 V.

Solution

On a Es = 15 V, une tension essentiellement continue. Le changement de flux requis pour atteindre la saturation est:

Δθ  = 950 mWb - 800 mWb = 150 mWb

de l'équation 18-6 on obtient:

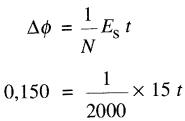
d'où t = 20 s

Le transformateur devient saturé après 20 secondes.

Cet exemple met en évidence le fait que même de très faibles tensions parasites peuvent affecter un grand réseau si elles durent assez longtemps.

Résumé

Dans cette section, nous avons appris à utiliser la loi de l'induction électromagnétique de Faraday dans sa forme la plus générale. Selon cette loi, une tension est induite à l'intérieur d'une boucle par un flux qui varie avec le temps. Cette tension est proportionnelle au taux de changement Δθ/Δt du flux dans la boucle. Pour une bobine, le tension est multipliée par le nombre de spires.

La loi de Lenz permet de trouver la polarité de la tension induite. D'après cette loi, la polarité est telle qu'un courant imaginaire sortant par la borne + de la boucle ou de la bobine crée un flux s'opposant à la variation du flux imposé. Cette loi s'applique même si la boucle porte déjà un courant. Nous avons vu aussi que l'application de la loi de l'induction permet de mesurer le flux en calculant les volts-secondes associés à la tension induite.

De la même façon. une tension continue, même très faible, appliquée à une bobine pendant un certain temps produit un flux qui croit proportionnellement aux volts-secondes et peut éventuellement provoquer la saturation du circuit magnétique.

PROBLÈMES

Niveau pratique

18-1 De quoi dépend la valeur de la tension induite dans une bobine?

18-2 Qu'entend-on par induction mutuelle?

18-3 Quelle est la loi qui donne la polarité de la tension induite dans une bobine? Énoncer cette loi.

18-4 Une bobine de 200 spires est traversée par un flux de 3 mWb provenant d'un aimant permanent. On éloigne l'aimant et le flux baisse à 1,2 mWb en 0,2 s. Calculer la valeur moyenne de la tension induite.

Niveau intermédiaire

18-5 Dans la Fig. 13-25 du chapitre 13, les deux bobines principales créent un flux de 15 Wb lorsque le courant d'excitation total est de 165 A.

a) Si le courant est graduellement réduit à zéro dans un intervalle de 2 secondes, quelle sera la tension induite dans chacune des bobines auxiliaires, ces dernières étant ouvertes?

b) Quelle est la tension induite dans chaque bobine principale?

18-6 Dans la Fig. 18-12, une bobine de 500 spires entoure un aimant permanent ayant un diamètre de 30 mm. En retirant la bobine lentement, on constate qu'on peut maintenir une tension de 40 mV pendant 6 secondes après quoi la tension devient nulle.

a) Quelle est la densité de flux développé par l'aimant?

b) Si l'on retirait la bobine en 0,3 seconde, quelle serait la valeur moyenne de la tension induite?

18-7 Appliquer la loi de Lenz à la Fig. 18-9 et montrer que les polarités doivent être telles qu'indiquées.

18-8 Appliquer la loi de Lenz aux Fig. 18-8a et 18-8b, et montrer que les électrons doivent circuler dans le sens indiqué.

18-9 Dans la Fig. 19-4b de la section Inductance, quelle est la polarité de la borne 1 lorsqu'on ouvre l'interrupteur?

18-10 Dans la Fig. 18-6, quelle est la polarité de la borne m par rapport à n à l'instant indiqué?

18-11 Dans la Fig. 19-6a du chapitre 19, quelle est la polarité de la borne 1 par rapport à 2?

18-12 Dans la Fig. 14-8 du chapitre 14, quelle est la polarité de la borne b par rapport à a lorsque le courant diminue?

18-13 Dans la Fig. 18-5, montrer de quelle façon les bobines A et B sont enroulées autour du noyau, sachant que le sens du flux et la polarité des tensions sont tels qu'indiqués.

Réponses

4) 1,8V; 5a) 1590V; 5b) 9750V; 6a) 0,68T; 6b) 0,8V

9) négative; 10) négative; 11) négative; 12) positive