
Loi d'ohm
La loi d'Ohm trouve des applications dans tous les domaines de l'électrotechnique. Cette section explique la loi, de même que l'utilisation d'un voltmètre et d'un ampèremètre dans un circuit électrique.
Production d'électricité, différence de potentiel
Le rôle des sources d'électricité est de transformer l'énergie mécanique, chimique, thermique ou radiante en énergie électrique. Elles réalisent cette transformation en maintenant constamment entre leurs deux bornes une différence dans la population d'électrons.
Elles soutirent des électrons d'une borne et les accumulent sur l'autre; une borne aura donc un manque d'électrons tandis que l'autre présentera un surcroît d'électrons.
La première sera donc positive car la charge des noyaux des atomes ne sera plus exactement équilibrée par celle des électrons; la surabondance d'électrons négatifs à la deuxième borne lui donnera une charge électrique résultante négative.
Les figures 3-1 et 3-2 montrent huit types de sources d'électricité.
Figure 3-1 Détails sur quelques sources d'électricité

Figure 3-2 Détails sur quelques sources d'électricité

Il est important de noter que ces générateurs d'électricité ne créent pas plus d'électricité qu'une pompe hydraulique ne fabrique de l'eau : l'électricité, nous l'avons vu, comprend la distribution et le mouvement des électrons localisés dans la matière.
Lorsque les deux bornes d'un appareil présentent respectivement un défaut (+) et un excès (-) d'électrons, on dit qu'il existe entre elles une différence de potentiel (en abrégé d.d.p.).
Cette différence de potentiel électrique, appelée très souvent tension électrique, ou force électromotrice, peut être avantageusement comparée à la pression développée par une pompe hydraulique dont la valve est fermée: elle peut exister même s'il n'y a pas de courant d'eau.
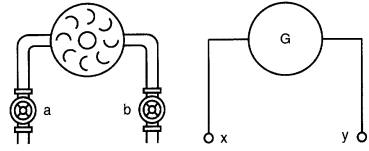
Ainsi, dans la Fig. 3-3, la différence de pression hydraulique entre les points a et b de la pompe peut être comparée à la différence de potentiel électrique entre les bornes x et y du générateur G.
Figure 3-3 La différence de potentiel entre les bornes x et y d'une génératrice peut être comparée à la différence de pression développée par une pompe entre les points a et b.
Unité de différence de potentiel
L'unité SI de différence de potentiel électrique (ou tension) est le volt (symbole V), tiré du nom du célèbre physicien italien Volta. Le kilovolt (kV) et le millivolt (mV) sont des multiples et sous-multiples du volt qui valent respectivement 1000 volts et 1/1000 de volt.
La différence de potentiel, ou tension, se représente par le symbole E et se mesure à l'aide d'un appareil appelé voltmètre (Fig. 3-4).
Figure 3-4 Ce voltmètre numérique permet de lire les tensions continues de zéro à 1000 V avec une précision de 0,05 %. Il peut aussi mesurer les tensions alternatives. Cet instrument très flexible permet aussi de mesurer les courants continus et alternatifs, la résistance, les fréquences, et la température.

Polarité
On identifie la borne qui présente un excès d'électrons par un signe (-), celle qui comporte un manque d'électrons, par un signe (+).
Ces deux bornes sont nommées respectivement borne négative et borne positive. Elles possèdent respectivement une polarité négative et une polarité positive.
Charges électriques
Les appareils qui reçoivent et transforment l'énergie électrique produite par les générateurs se nomment charges (voir Fig. 3-5). Les trois principaux types sont :
1. Les charges qui transforment l'énergie électrique en travail.
Exemples: moteurs, vibrateurs électriques, électroplongeurs.
2. Les charges thermiques dans lesquels l'énergie électrique est transformée en chaleur.
Exemples: grille-pain, chaufferettes, fers à repasser, lampes à incandescence, fours industriels.
3. Les charges chimiques où l'énergie électrique est transformée en énergie chimique.
Exemples: bains à galvanoplastie qui servent à plaquer du chrome sur les objets; bacs à électrolyse servant à produire l'aluminium, piles rechargeables.
Figure 3-5 Quelques exemples de charges électriques avec leur symbole.
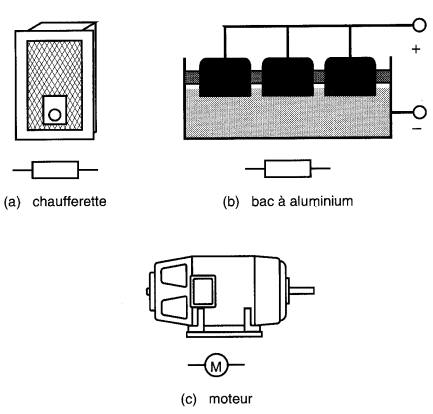
Il existe bien d'autres appareils et dispositifs qui agissent comme charges électriques. Mentionnons les téléviseurs et les lampes fluorescentes qui transforment l'énergie électrique en énergie radiante visible, de même que toute la gamme des équipements électroniques de commande et de puissance.
Courant dans un conducteur et dans une source
Nous avons vu à la section Nature de l'électricité, Fig. 2-5, que le sens conventionnel du courant est l'inverse du sens de déplacement des électrons.
Dans une charge le courant conventionnel se dirigera de la borne positive (+) à la borne (-). Dans une source le courant passera de la borne négative (-) à la borne positive (+). Le courant qui conserve toujours le même sens est appelé courant continu.
Nous verrons plus loin qu'il existe également des courants qui changent périodiquement de sens : on les appelle courants alternatifs. Les premiers chapitres de ce livre porteront exclusivement sur l'étude des courants continus et de leurs effets.
Analogie hydraulique
Il est parfois plus facile de comprendre ce qu'est le courant électrique en faisant une comparaison avec un système hydraulique. La partie pointillée du schéma de la Fig. 3-6 représente un tuyau partiellement rempli de sable.
Figure 3-6 Pompe et sa charge
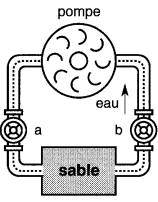
La différence de pression développée par la pompe fait circuler l'eau dans le circuit hydraulique. On peut imaginer que l'eau est composée de milliers de gouttes, qui rencontreront une certaine opposition dans leur passage à travers le sable.
De la même façon, à la Fig. 3-7, la différence de potentiel électrique du générateur fait circuler des électrons à travers l'élément d'une chaufferette.
Figure 3-7 Génératrice et sa charge
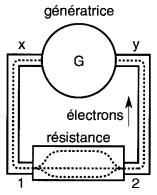
Ces électrons (analogues aux gouttes d'eau) rencontrent une certaine opposition à leur passage, car ils rencontrent les atomes du métal qui se trouvent dans leur chemin. Cette opposition dans le cas de l'élément d'une chaufferette est assez considérable ; c'est pourquoi on l'appelle résistance.
Le frottement entre les électrons et les atomes produit un dégagement de chaleur. Dans la Fig. 3-7 la génératrice (une source) est raccordée à la résistance (une charge) au moyen de deux fils xl et y2.
Les fils sont choisis afin qu'ils ne présentent à peu près aucune opposition au passage du courant électrique. Il en résulte que la différence de potentiel aux bornes x et y de la source apparaît entièrement aux bornes 1 et 2 de la charge.
D'une façon générale, et quelle que soit sa nature, une charge s'oppose toujours au passage d'un courant électrique. C'est précisément cette opposition qui permet à la charge de recevoir et de convertir l'énergie électrique.
Unité d'intensité de courant
Le courant hydraulique (Fig. 3-6) pourrait se mesurer par le nombre de gouttes qui passent en un point par seconde, et le courant électrique (Fig. 3-7) par le nombre d'électrons par seconde. De telles unités ne seraient évidemment pas pratiques.
En électricité, l'unité SI d'intensité de courant est l'ampère (symbole A).
Ce mot a été adopté en l'honneur du savant français André Ampère. Un ampère équivaut au passage de 6,2 milliards de milliards (6,2 x 1018) d'électrons par seconde.
Pour fixer l'ordre de grandeur d'un ampère, qu'il suffise de se rappeler qu'une lampe à incandescence de 100 watts tirera un courant de près d'un ampère sous la tension de 120 volts.
L'intensité d'un courant (représenté par la lettre I) s'exprime donc en ampères. Elle se mesure à l'aide d'un appareil appelé ampèremètre (Fig. 3-8).
Pour des intensités de courant moins élevées, on emploie couramment le milliampère (mA) qui vaut un 1/1000 d'ampère.
Figure 3-8 Cet ampèremètre numérique permet de mesurer les courants continus de zéro à 1000 A avec une précision de 2 %. Il peut aussi mesurer les courants alternatifs. La pince qui entoure le fil permet de mesurer le courant circulant dans ce conducteur sans que l'on soit obligé de le couper. Cette mesure de courant par induction est expliquée à la section 31.6 du chapitre sur les transformateurs spéciaux.

Mesures d'une intensité de courant et d'une tension Pour mesurer le nombre d'électrons qui passent, par seconde, dans l'élément d'une chaufferette, on place un ampèremètre entre le générateur et l'élément, de façon qu'il soit traversé par tous les électrons (voir Fig. 3-9, montage en série).
Figure 3-9 Raccordement d'un ampèremètre
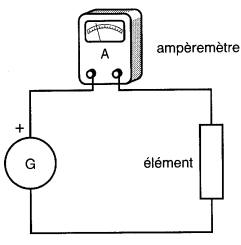
Dans le cas d'un ampèremètre analogique, une aiguille se déplace devant un cadran gradué en ampères et sa position donne l'intensité du courant. Un ampèremètre numérique affiche la valeur du courant directement.
Pour déterminer la différence de potentiel (ou la tension électrique) entre les extrémités de l'élément, on relie les deux bornes d'un voltmètre (V) à ces deux points (voir Fig. 3-10, montage en parallèle ou en dérivation).
Figure 3-10 Raccordement d'un voltmètre
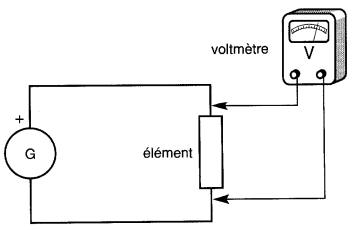
Dans le cas d'un voltmètre analogique, une aiguille s'arrête devant une division du cadran et indique, en volts, la valeur de la tension mesurée. Un voltmètre numérique affiche la tension directement.
Contrairement à l'ampèremètre, le voltmètre ne laisse passer que très peu d'électrons, de sorte que sa présence ne modifie pratiquement pas la différence de potentiel entre les bornes de l'élément chauffant.
Fait important à retenir: l'ampèremètre est intercalé dans le conducteur qui mène à l'élément, tandis que le voltmètre est branché directement aux deux extrémités de l'élément.
Loi d'Ohm La Fig. 3-11 montre comment sont disposés l'ampère-mètre (A) et le voltmètre (V), destinés à mesurer, respectivement, l'intensité du courant qui parcourt la chaufferette et la tension à ses bornes.
Figure 3-11 Le rapport entre la tension et le courant est un nombre constant appelé résistance
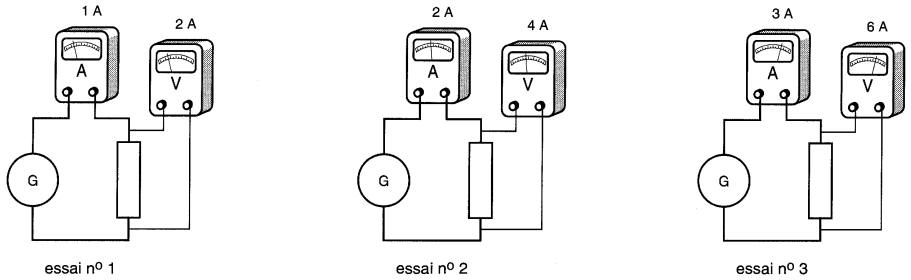
Supposons qu'au moment où la lecture est prise, Fig. 3-11, (essai n° 1), le générateur applique une différence de potentiel de 2 volts et que le courant I résultant soit de 1 ampère.
Le rapport de la tension au courant égale:
E/I = 2 volts / 1 ampère = 2
Agissons maintenant sur le générateur, Fig. 3-11 (essai n° 2), de manière que la tension aux bornes de l'élément, indiquée par le voltmètre, soit de 4 volts. On constate alors que l'ampèremètre marque 2 ampères.
Le rapport de la tension au courant égale :
E/I = 4 volts / 2 ampère = 2
Reprenons l'expérience, Fig. 3-11 (essai n° 3), en appliquant 6 volts à la chaufferette; l'ampèremètre indique maintenant 3 ampères.
Encore une fois, le rapport:
E/I = 6 volts / 3 ampère = 2
On voit donc que le courant est d'autant plus grand que la tension est grande : en doublant la tension, l'intensité du courant double, en triplant la tension, l'intensité du courant triple.
C'est en partant des résultats d'une expérience semblable que le physicien allemand Georg-Simon Ohm énonça en 1827 la loi suivante : le rapport entre la tension appliquée aux bornes d'un conducteur et le courant qui le parcourt est un nombre constant.
Ce nombre constant caractérise une propriété du conducteur: sa résistance.
La résistance d'un corps quelconque est l'opposition qu'il offre au passage du courant.
La résistance se représente par le symbole R.
La formule de la loi d'Ohm s'écrit:
tension / courant = résistance
ou encore, en abrégé
E / I = R (3-1)
Unité de résistance
L'unité SI de résistance est l'ohm (symbole Ω). Ω est une lettre grecque qui se prononce «omega».
D'après la définition SI, l'ohm est la résistance électrique qui existe entre deux points d'un conducteur lorsqu'une différence de potentiel constante de 1 volt appliquée entre ces deux points produit dans ce conducteur un courant de 1 ampère, ce conducteur n'étant le siège d'aucune force électromotrice.
Dans la formule de la loi d'Ohm, si la tension E est exprimée en volts et le courant I en ampères, la résistance R sera exprimée en ohms.
Exemple: 18 volts / 3 ampères = 6 ohms.
Application de la loi d'Ohm
Maintenant que nous connaissons la relation qui existe entre une tension de E volts appliquée aux extrémités d'un élément possédant une résistance de R ohms et parcouru par un courant de I ampères, il est facile, en connaissant deux de ces facteurs, de déterminer le troisième.
Ainsi l'équation (3-1) peut être exprimée sous les formes:
E / R = I
ou volts / ohms = ampères (3-2)
et
E = RI
ou volts = ohms x ampères (3-3)
Trois cas peuvent alors se présenter :
1. On connaît la tension E et le courant I, on cherche la résistance R.
2. On connaît la tension E et la résistance R, on cherche le courant I.
3. On connaît le courant I et la résistance R, on cherche la tension E.

Ces trois cas, résumés dans le tableau 3-1, sont illustrés par les exemples numériques suivants.
Exemple 3-1
Lorsqu'on branche un réchaud électrique à une source de tension E de 120 volts, il est parcouru par un courant I de 5 ampères.
Trouver la résistance R de l'élément du réchaud.
Solution
En appliquant la forme (3-1) de la loi d'Ohm, la résistance est donnée par:
E / I = R = 120 volts / 5 ampères = 24 ohms
Figure 3-12 Voir exemple 3-1

Exemple 3-2
Une puissante lampe à incandescence ayant une résistance R de 10 ohms est alimentée sous une tension E de 120 volts.
Quelle sera l'intensité I du courant tiré par cette lampe
Solution
La forme (3-2) de la loi d'Ohm donne :
E / R = I = 120 volts / 10 ohms = 12 ampères
Exemple 3-3
Déterminer la chute de tension E dans un fil conducteur dont la résistance R est de 50 milliohms, sachant qu'il porte un courant I de 300 ampères.
Solution
D'après la forme (3-3) de la loi d'Ohm:
E = RI = 50 x 10-3 ohms x 300 ampères = 15 V
La solution du problème suivant fait intervenir deux des cas précédents.
Exemple 3-4
Un fer à repasser alimenté par un réseau de distribution dont la tension est de 120 volts est parcouru par un courant de 6 ampères.
Si la tension du réseau tombe à 100 volts, quelle sera la nouvelle intensité du courant?
Figure 3-13 Voir exemple 3-4

Solution
Pour un appareil donné, le courant dépend de la tension appliquée, laquelle est généralement fixée par le réseau. Le seul facteur qui, ordinairement, ne varie pas, est la résistance, qui est une caractéristique de l'appareil.
Il faut donc, en premier lieu, trouver la résistance R du fer à repasser:
R = E / I= 120V / 6A = 20 Ω
Connaissant la résistance de l'appareil et la nouvelle tension appliquée, le courant résultant sera :
I = E / R = 100V / 20 Ω = 5 A
Sachant que le courant est toujours proportionnel à la tension appliquée, le nouveau courant aurait pu être calculé par une simple règle de trois:
I = 6 A x 100V / 120V = 5A
Résumé
Dans cette section nous avons introduit trois grandeurs fondamentales en électricité : la tension ou différence de potentiel, le courant et la résistance.
Nous avons aussi appris qu'il existe deux grandes catégories d'appareils électriques: les sources et les charges. Les sources d'électricité permettent d'imposer une différence de potentiel ou tension électrique entre deux bornes.
L'une des bornes présentant un défaut d'électrons est la borne positive (+) et l'autre ayant un excès d'électrons est la borne négative (-). Dans le cas d'une source, cette différence de potentiel est aussi appelée force électromotrice.
L'unité SI de différence de potentiel (ou tension) est le volt (symbole V).
Les appareils qui sont branchés aux bornes d'une source pour transformer l'énergie électrique sont des charges.
Ces charges peuvent transformer l'énergie électrique produite par la source en énergie mécanique (ex. : moteurs), thermique (ex. : appareils de chauffage) ou chimique (ex. : bacs à galvanoplastie, piles en charge).
Dans un circuit formé d'une source et d'une charge, circule un courant électrique. L'unité de courant électrique est l'ampère (symbole A).
Si le courant circule toujours dans le même sens, on dit que c'est un courant continu.
Par contre s'il change de sens périodiquement, il s'agit d'un courant alternatif. On utilise un ampèremètre pour mesurer un courant électrique et un voltmètre pour mesurer une tension électrique ou différence de potentiel entre deux points d'un circuit.
L'ampèremètre doit être branché en série avec l'appareil dont on veut mesurer le courant alors que le voltmètre doit être branché en parallèle avec l'appareil dont on veut mesurer la tension.
Enfin, la loi d'Ohm, une des lois les plus importantes régissant le fonctionnement des circuits électriques s'énonce comme suit :
le rapport entre la tension appliquée aux bornes d'un conducteur et le courant qui le parcourt est un nombre constant appelé résistance.
La résistance est une grandeur caractéristique de ce conducteur. L'unité de résistance est l'ohm (symbole Ω).
La loi d'Ohm permet de calculer une des grandeurs suivantes : tension, courant ou résistance lorsque les deux autres sont connues.
Figure 3-14 ré Ohmmètres pour mesurer la résistance de l'isolation d'un système ou d'un dispositif sous une tension continue de 250 V ou 100 V. Ces instruments peuvent mesurer des résistances comprises entre 10 kΩ et 1000 MΩ. L'échelle donne à la fois une lecture analogique et numérique.

PROBLÈMES
Niveau pratique
3-1 Quel est le rôle des générateurs d'électricité?
3-2 Pourquoi une borne présentant un manque d'électrons est-elle positive?
3-3 Les générateurs créent-ils de l'électricité?
3-4 Quelle est l'unité SI de tension électrique? Nommer une unité plus grande.
3-5 Nommer trois types de charges électriques.
3-6 La borne d'un accumulateur qui comporte une surabondance d'électrons a-t-elle une polarité positive?
3-7 Soit un conducteur reliant les deux bornes d'une pile. Les électrons se déplacent-ils dans le conducteur du pôle positif au pôle négatif, ou vice versa? Quel est le sens conventionnel du courant dans le conducteur?
3-8 Quelle est l'unité SI d'intensité de courant? Nommer une unité plus petite.
3-9 Quel appareil utilise-t-on pour mesurer le courant?
3-10 Les ampèremètres et les voltmètres sont-ils raccordés de la même façon? Tracer des schémas illustrant la mesure d'une intensité de courant et la mesure dune tension.
3-11 Énoncer la loi d'Ohm.
3-12 Quelle est l'unité SI de résistance? Niveau intermédiaire
3-13 Exprimer en kilovolts une tension de 4000 volts.
3-14 Exprimer une intensité de 0,2 ampères en milliampères.
3-15 Quelle est la résistance d'un conducteur parcouru par une intensité de 3 ampères lorsqu'on lui applique une tension de 6 volts?
3-16 Une chauffe-eau absorbe 15A sous 120V. Calculer sa résistance.
3-17 Calculer le courant circulant dans un élément de cuisinière électrique ayant une résistance de 10Ω, alimenté par une tension de 240 V.
3-18 Un fer à souder est alimenté à 120 V. Sachant que sa résistance est de 50 ohms, calculer le courant tiré.
3-19 On désire faire circuler un courant de 4 A dans un rhéostat de 7Ω. Quelle tension doit-on lui appliquer?
3-20 Calculer la chute de tension dans un fil de 8Ω lorsqu'il est parcouru par un courant de 15 ampères.
3-21 Une ligne de transport ayant une résistance de 6 ohms est traversée par un courant de 400 A. Quelle est la chute de tension en kilovolts?
3-22 Une chauffe-eau tire un courant de 15 A sous une tension de 240 volts. Quel courant tirera-t-il si la tension baisse à 210 volts?
3-23 L'enroulement du champ d'une génératrice de 500 mégawatts possède une résistance de 62,6 mΩ. Quelle tension doit-on appliquer pour y faire circuler un courant de 4060 A?
3-24 Un éclair moyen implique un courant de 20 kA et une tension de 200 MV. Calculer la valeur de la résistance offerte au passage du courant.
Réponses
13) 4 kV;
14) 200 mA;
15) 2Ω;
16) 8Ω;
17) 24 A;
18) 2,4 A;
19) 28 V;
20) 120 V;
21) 2,4 kV;
22) 13,1 A;
23) 254 V;
24) 10 kΩ
