La machine asynchrone: relations fondamentales
Cet appendice constitue un complément à la section La machine asynchrone: circuit équivalent et variation de la vitesse sur le moteur asynchrone.
Nous y développons les formules de base qui décrivent le comportement de la machine lorsqu'on fait varier la tension et la fréquence.
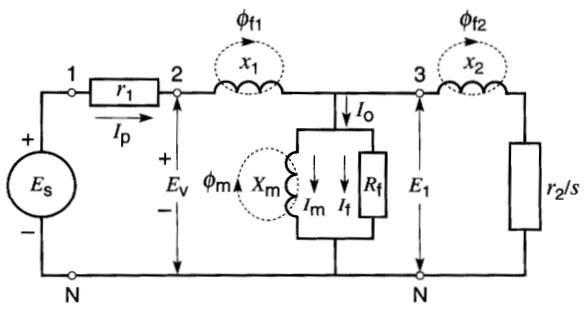
La Fig. A5-1 montre le circuit équivalent d'une phase d'un moteur asynchrone.
Fig. A5-1 Circuit équivalent d'un moteur à rotor bobiné où tous les éléments sont rapportés au primaire (stator)

Elle correspond à la Fig. 35-5, de la section La machine asynchrone: circuit équivalent et variation de la vitesse.
Les réactances de fuite x1 et x2 sont associées aux flux de fuite Φf1, et Φf2.
La réactance mutuelle Xm est associée au flux mutuel Φm, lequel est créé par le courant magnétisant Im.
La tension Ev entre les points 2 et N est égale à la somme des tensions induites par le flux mutuel Φm et le flux de fuite Φf1.
La chute de tension x1Ip est toujours faible par rapport à la tension E1; par conséquent, Ev est presque égale à E1.
Cela nous permet de déplacer la branche d'excitation en amont de la réactance x1, soit entre les bornes 2 et N (Fig. A5-2).
Figure A5-2 Déplacement de la branche d'excitation et élimination de la résistance Rf.
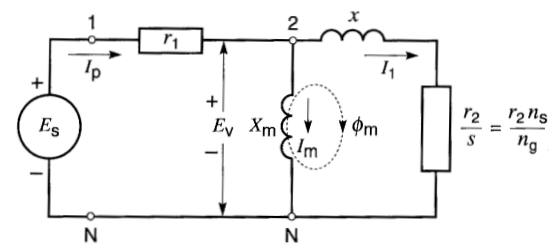
De plus, on élimine la résistance Rf car son effet est négligeable sur la performance du moteur.
Ces modifications influencent légèrement le comportement du moteur, mais elles mettent en évidence ses caractéristiques principales. Ainsi, on peut combiner les réactances x1 et x2 en une seule réactance de fuite x.
Celle-ci correspond essentiellement à la réactance de fuite du moteur, rapportée au stator.
Au lieu de résoudre le circuit à partir de la source Es, nous étudierons plutôt le circuit situé à droite de la tension Ev.
L' amplitude de la tension Ev sera contrôlée en ajustant la tension Es de la source pour compenser la faible chute de tension r1Ip.
Le glissement traditionnel s est égal à (ns - n)/ns = ng/ns, où ng est la vitesse de glissement.
On peut donc remplacer la «résistance de puissance» r2/s par:
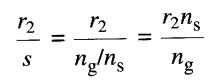
Cette façon de représenter la résistance de puissance est montré à la Fig. A5-2.
Procédons maintenant à l'analyse de ce circuit.
Flux mutuel dans le moteur
Tout comme dans un transformateur, la relation entre la tension appliquée et le flux mutuel dans un moteur est donnée par l'équation:

En réarrangeant les termes on obtient:
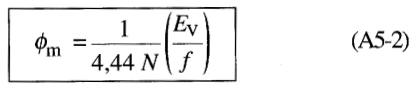
L' équation A5-2 indique que le flux mutuel dépend du rapport (Evlf).
Tant et aussi longtemps que ce rapport est gardé fixe, le flux mutuel demeurera constant. Cependant, on peut diminuer le flux en réduisant Evlf, soit en baissant la tension Ev, soit en augmentant la fréquence f.
En général, il est préférable de maintenir le rapport égal à EsN/fN, où EsN et fN sont respectivement la tension et la fréquence nominale du moteur.
Le rapport Evlf s'exprime en volts par hertz. Comme nous le verrons plus loin, ce rapport sert à exprimer les caractéristiques du moteur asynchrone.
Décrochage: vitesse de glissement
Un moteur asynchrone décroche lorsque le couple atteint sa valeur maximale. Pour une tension Ev donnée, cette condition se produit lorsque la résistance r2/s (ou r2nslng) atteint une valeur numérique égale à la réactance de fuite x.
La Fig. A5-3 montre le circuit du moteur dans ces circonstances.
Figure A5-3 Circuit équivalent lors du décrochage.
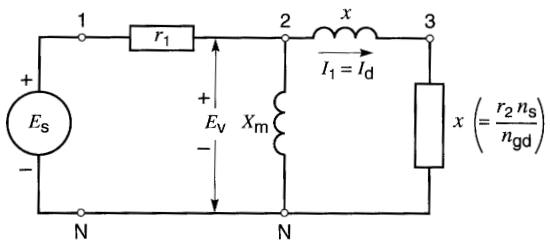
On constate que la résistance de puissance (r2/s) possède alors une valeur résistive de x ohms.
En désignant la vitesse de glissement lors du décrochage par le symbole ngd, on peut écrire:

soit:

où
ngd = vitesse de glissement lors du décrochage [r/min]
ns = vitesse svnchum [r/min]
r2 = résistance équivalente du rotor rapportée au stator [Ω]
X = réactance de fuite moteur rapportée au stator [Ω]
Examinons de plus près la signification de ngd lorsque la tension et la fréquence varient.
On se souvient que:

et que

où L est l'inductance de fuite du moteur rapportée au stator.
On peut donc écrire:
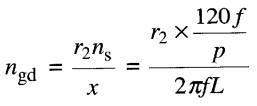
soit:
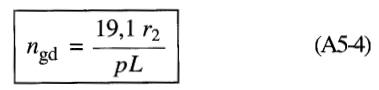
L'équation A5-4 révèle que pour une machine asynchrone donnée, la vitesse de glissement ngd est une constante.
Elle dépend uniquement de la résistance r2 du rotor, de l'inductance de fuite L et du nombre de pôles p.
Notamment, ngd est indépendante de la tension et de la fréquence appliquées au stator. C'est un résultat assez remarquable.
La constance de ngd nous incite à la choisir comme vitesse de référence.
La vitesse nd lors du décrochage est donnée par:
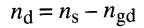
où ns est la vitesse synchrone alors en vigueur.
Exemple A5-1
Un moteur asynchrone de 4 piles possède une réactance de fuite de 6,4 S2 lorsqu'il est alimenté à une fréquence de 50 Hz.
Sachant que la résistance du rotor rapportée ati stator est de 1,2 Ω.
Calculer:
a) la vitesse de glissement lors du décrochage
b) la vitesse de rotation lors du décrochage lorsque le moteur est alimenté par une source de 217 V à 34 Hz
Solution
a) Vitesse de glissement lors du décrochage :
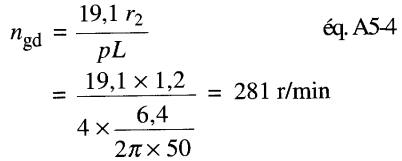
b) Vitesse synchrone à une fréquence de 34 Hz :
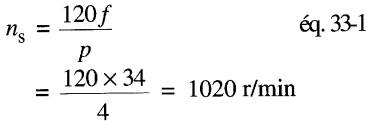
Vitesse de rotation lors du décrochage sous une tension de 217 V, 34 Hz:

Décrochage: valeur du courant rotorique Id
En se référant à la Fig. A5-3, où la résistance de puissance possède toujours une valeur résistive de x ohms, on trouve que l'impédance Zd de la branche 2-3-N est:
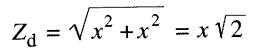
Le courant I, lors du décrochage a donc une valeur Id donnée par:
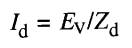
soit:

Si l'on exprime Id en fonction des paramètres du moteur on obtient:
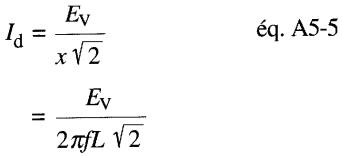
soit:
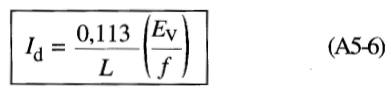
Lorsqu'on connaît Ev, L et f on peut facilement calculer la valeur du courant de décrochage Id.
Il n'y a pas de restriction sur les valeurs de Ev et f, sauf que, pour éviter la saturation, le flux mutuel ne doit pas dépasser sa valeur nominale. Rappelons que le courant Id représente le courant rotorique ramené au stator.
Le courant total tiré par le moteur est supérieur à Id car il comprend le courant de magnétisation Im.
Décrochage: valeur du couple Td
La puissance Pr fournie au rotor lors du décrochage (Fig. A5-3) est donnée par:
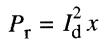
Donc, pour une phase, le couple Td lors du décrochage est donné par:

donc:
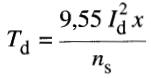
Sachant que:

on obtient:
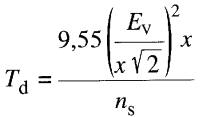
d'où:

On peut exprimer Td en fonction des paramètres du moteur, comme suit:
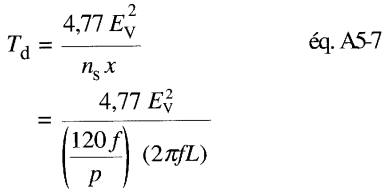
soit:
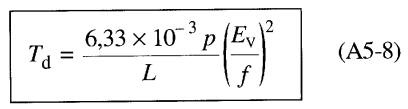
On constate que le couple de décrochage demeure constant pour autant que le rapport Ev/f soit constant.
Donc, tout comme dans le cas du courant de décrochage, le couple de décrochage reste constant lorsque le flux mutuel est maintenu constant.
Facteur de glissement g et choix des grandeurs de base
Dans les années précédant l'arrivée des variateurs de vitesse, la fréquence appliquée aux moteurs asynchrones était fixe, soit généralement 60 Hz ou 50 Hz.
Comme la vitesse synchrone ns était constante, elle servait de base de référence.
De plus, on misait sur le glissement s = (ns - n)/n, pour décrire la vitesse du moteur.
Enfin, on prenait comme autres bases le couple nominal TN et le courant nominal IN du moteur.
Cependant, maintenant que l'on peut faire varier la fréquence et la tension, il est préférable de prendre comme base, non pas la vitesse synchrone n, mais plutôt la vitesse de glissement ngd lors du décrochage.
De plus, au lieu de choisir le couple nominal comme base de référence, on utilise le couple de décrochage Td.
Enfin, on utilise le courant de décrochage Id comme courant de référence.
En effet, en choisissant ngd, Td, et Id comme bases de référence, on simplifie de beaucoup le calcul des vitesses, des couples et des courants sous charge.
Dans cette optique, nous définissons un nouveau paramètre, appelé facteur de glissement g. Il est égal au rapport de la vitesse de glissement ng sous charge et de la vitesse de glissement du décrochage ngd.
On peut donc écrire:
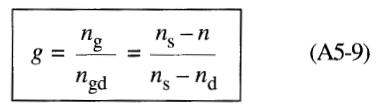
Où les symboles ont la signification habituelle.
Exemple A5-2
Un moteur à 6 pôles alimenté par une source a 63,3 Hz décroche à une vitesse nd de 1030 r/min. Lorsque le moteur fonctionne sous charge à une fréquence de 71.4 Hz, on constate que sa vitesse est de 1373 r/min.
Calculer le facteur de glissement g.
Solution
Vitesse de glissement ngd lors du décrochage:
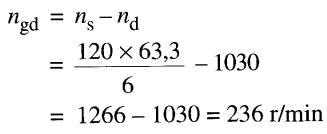
Vitesse de glissement ng sous charge:
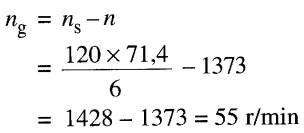
Le facteur de glissement sous charge est donc:
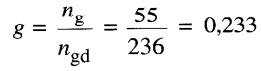
Courant I. en fonction de g
On a vu (Fig. A5-2) que l'on peut exprimer la résistance de puissance sous la forme r2ns /ng.
D'autre part, lors du décrochage:

et le facteur de glissement g est donné par:

En combinant ces deux expressions on obtient le résultat:

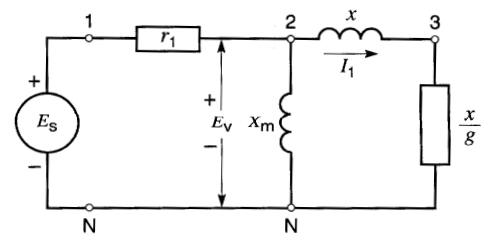
On peut donc exprimer la résistance de puissance en fonction de la réactance de fuite x et du facteur de glissement g. Cela est mis en évidence dans le circuit de la Fig. A5-4.
Figure A5-4
Circuit équivalent lorsque le facteur de glissement g (au lieu du glissements) est utilisé comme paramètre variable
Notez que g peut prendre n'importe quelle valeur, positive ou négative.
L'impédance de la branche 2-3-N est donnée par:
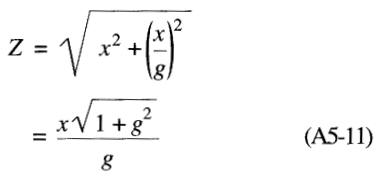
e courant Il dans le rotor est donc:
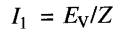
alors:

Mais on se souvient que le courant de décrochage Id est donné par:

En combinant les équations A5-5 et A5-12 on obtient:
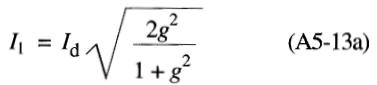
On peut donc exprimer le courant Il en fonction du courant Id et du facteur de glissement g.
La valeur normalisée de Il est donnée par l'expression
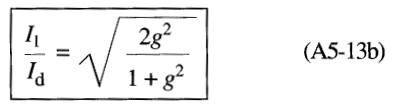
Cette expression est illustrée graphiquement à la Fig. A5-5.
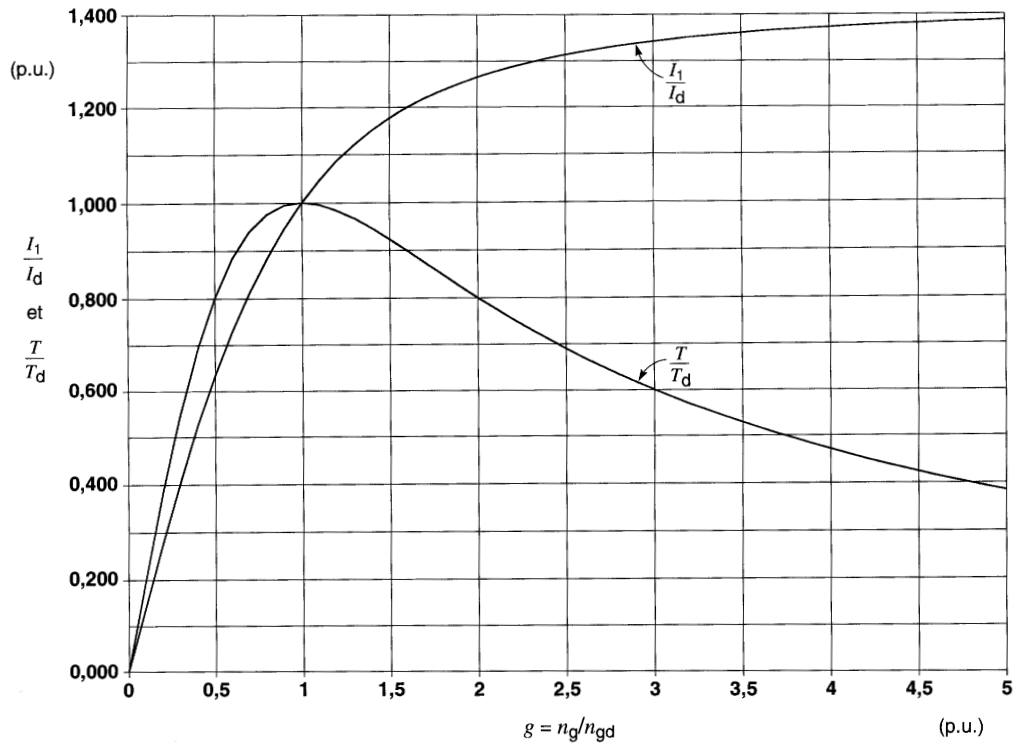
Figure A5-5
Courbes normalisées montrant la relation entre le couple relatif T/Td et le courant relatif Il/Id, en fonction du facteur de glissement ng/ngd.
Exemple A5-3
Le courant de décrochage Id d'un moteur asynchrone est de 359 A et la vitesse de glissement n gd est de 115 r/min.
Le flux mutuel étant constant, calculer le courant rotorique lorsque la vitesse de glissement ng est de 45 r/min.
Solution
Le facteur de glissement est:
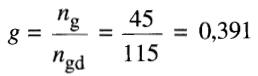
on peut donc écrire:
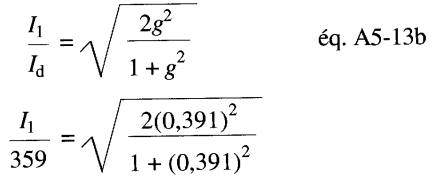
d'où:
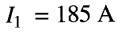
Couple T en fonction de g
En se référant de nouveau à la Fig. A5-4, la puissance fournie au rotor est donnée par:
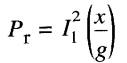
Le couple T est donc:
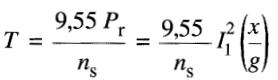
En utilisant la formule A5-12 on obtient:
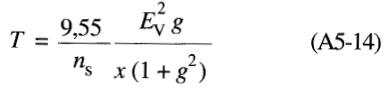
Ensuite, en combinant les équations A5-14 et A5-7 on obtient une expression du couple T en fonction du couple de décrochage Td et du facteur de glissement g:
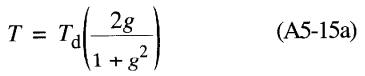
La valeur normalisée de Test donnée par l'expression:
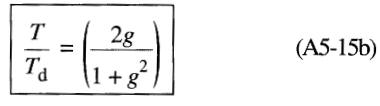
L'équation A5-15b nous permet de tracer la courbe du couple relatif T/Td en fonction du glissement relatif g (= ng/ngd).
Cela donne le deuxième graphique de la Fig. A5-5.
Les graphiques de T/Td et Il /Id en fonction de g sont universels en ce sens qu'ils s'appliquent à n'importe quel moteur asynchrone polyphasé.
En effet, dès que l'on connaît le couple de décrochage Td, le courant de décrochage Id et la vitesse de glissement ngd, on peut déterminer le couple T, le courant Il et la vitesse de glissement ng, pour n'importe quelle condition de fonctionnement du moteur.
Relation linéaire entre T et ng
En regardant la Fig. A5-5, on observe que le graphique T/Td vs g est presque une droite entre l'origine et le point donné par T/Td = 0,6 et g = 1/3.
Il s'ensuit que dans cette région linéaire, T/Td = 1,8 g.
Dans un système à vitesse variable, la région comprise entre g = 0 et g = 1/3 correspond sensiblement à la plage de fonctionnement normal.
Par conséquent, la relation entre le couple T et la vitesse de glissement ng peut être exprimée par la formule approximative:
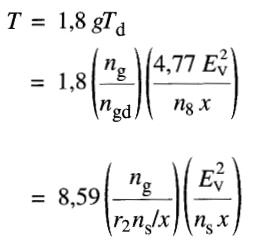
Le couple s'exprime donc comme suit en fonction des paramètres du moteur:
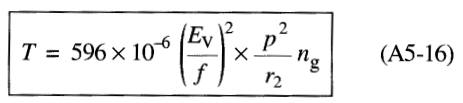
La formule A5-16 est valable pour tout moteur asynchrone pour autant que le glissement ng ≤ 1/3 ngd, ou encore que T ≤ 0,6 Td.
De plus, il n'y a aucune restriction sur les valeurs de Ev, r2, ns ou ng, sauf que le flux mutuel ne doit pas dépasser sa valeur nominale pour éviter la saturation.
Résumé
Dans cet appendice, nous avons développé plusieurs équations qui sont représentées par les deux graphiques de la Fig. A5-5.
Afin de consolider le tout et pour résoudre un problème quelconque, nous suggérons la procédure suivante:
1) À partir des données du
problème, déterminer les valeurs de ngd, Id et Td, en utilisant les équations
(A5-4), (A5-6) et (A5-8).
2) Vérifier que le rapport Evlf EsNlfN, où ESN et fN ont respectivement la tension nominale ligne à neutre et la fréquence nominale du moteur. Cela assurera que le flux mutuel ne dépassera pas la limite admissible.
3) En utilisant les données du problème et en appliquant les équations (A5-9), (A5-13b) et (A5-15b), déterminer les valeurs du facteur de glissement g, du courant I, du couple T et de la vitesse de glissement ng.
4) Pour une vitesse donnée, soit pour un facteur de glissement ng, les valeurs du courant I et du couple T peuvent aussi être obtenues graphiquement à partir des courbes de la Fig. A5-5.
Inversement, on peut déterminer g et donc la vitesse pour un couple T donné.
Liste des symboles
Aux fins de référence rapide, nous donnons ici la liste des symboles utilisés dans cet appendice.

