
Notions de mécanique
voir aussi
Les appareils électriques sont le siège de phénomènes mécaniques et thermiques, c'est pourquoi il importe d'avoir une bonne connaissance des lois fondamentales qui régissent ces deux domaines.
Cependant, avant d'entreprendre une étude de la mécanique et de la thermodynamique, il est indispensable de décrire le système d'unités adopté dans cette section.
Il s'agit du Système international d'unités, désigné universellement par l'abréviation SI.
Les unités SI
Le SI est un système métrique moderne qui a été adopté par tous les pays du monde.
En effet, les unités SI sont plus faciles à manipuler que les anciennes unités métriques et bien supérieures aux unités anglaises (gallon, pouce, etc.).
Le SI repose sur sept unités de base qui sont:
1. le kilogramme (kg), unité de masse.
2. le mètre (m), unité de longueur.
3. la seconde (s), unité de temps.
4. le kelvin (K), unité de température.
5. l'ampère (A), unité de courant électrique.
6. la mole (mol), unité de quantité de matière et
7. la candela (cd), unité d'intensité lumineuse.
Toutes les autres unités sont dérivées de ces unités de base, soit par des lois naturelles, soit par définition, soit par des relations géométriques.
C'est ainsi que le newton (N), unité de force, est égal à 1 kilogramme-mètre par seconde carrée (kg•m/s²), que le joule, unité d'énergie, est égal à 1 newton-mètre, et ainsi de suite.
Le tableau 1-1 présente une liste des unités SI utilisées dans cette section.
De plus, on donne une série de tables qui facilitent beaucoup la conversion des unités lorsque cette opération s'avère nécessaire. Le lecteur pourra également les consulter afin de mieux apprécier l'ordre de grandeur des diverses unités.

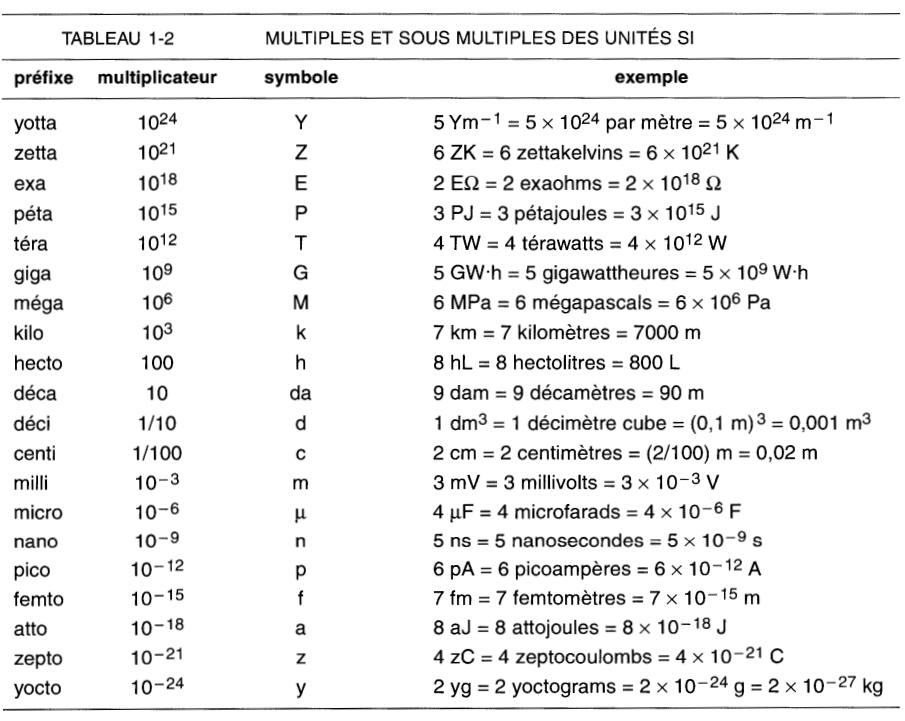
Multiples et sous-multiples des unités
Les multiples et sous-multiples des unités SI sont obtenus en faisant précéder ces unités de préfixes appropriés comme kilo, méga, nano, déci, etc.
Ces pré fixes multiplient la valeur de l'unité par les facteurs donnés dans le tableau 1-2.
Par exemple, 1 kilomètre = 1000 mètres, 1 millimètre = 0,001 mètre et 1 mégawatt = 106 watts ou 1 million de watts.
Emploi des exposants
En électricité comme dans toutes les disciplines scientifiques, on rencontre des grandeurs dont la valeur varie entre des limites énormes.
On doit, par exemple, pouvoir comparer la charge minuscule d'un électron avec celle, infiniment plus grande, d'un éclair, ou encore pouvoir mesurer des masses allant de la masse infime d'un atome à la masse énorme de la terre.
Le rapport entre la plus grosse et la plus petite valeur est tellement considérable qu'il a fallu trouver un moyen simple pour l'exprimer.
Par exemple, un courant électrique de 1 ampère seulement correspond au passage de 6 240 000 000 000 000 000 électrons par seconde.
Comment exprimer simplement des chiffres aussi grands?
On utilise les exposants, et plus particulièrement les puissances de 10.
D'après cette méthode, les expressions 10², 10³ et 104 correspondent respectivement aux nombres 100, 1000 et 10 000.
Les chiffres 2, 3, 4, etc., en position supérieure sont les exposants : on constate qu'ils indiquent le nombre de zéros suivant le chiffre 1.
Ainsi, 107 équivaut à 10 000 000.
De cette manière on peut écrire qu'un courant électrique de 1 ampère correspond au passage de 6,24 x 1018 électrons par seconde ; ce qui est plus court et moins sujet à erreur.
Par un raisonnement analogue, on exprime des quantités très petites en utilisant les exposants négatifs ; ainsi 10-3 équivaut à 1/(10³) = 1/1000.
Utilisation des symboles (+) et (-)
En arithmétique, on utilise les symboles (+) et (-) pour décrire les opérations d'addition et de soustraction.
En électricité et en mécanique, on étend leur signification pour indiquer le sens d'une force, d'un courant électrique, d'une vitesse, d'une puissance, etc., par rapport à une direction de référence choisie.
Par exemple, si un courant circulant dans un fil possède d'abord une valeur positive (+) et ensuite une valeur négative (-), cela indique qu'il a simplement changé de sens.
De la même façon, si la vitesse d'une machine passe de +1000 r/min à -400 r/min, cela indique que son sens de rotation a changé.
Dans les sections qui suivent, nous rencontrerons souvent cette signification des symboles (+) et (-).
Force
Dans le langage courant, on se soucie peu de faire une distinction entre les termes force, travail, énergie et puissance; cependant, chacun de ces mots a une signification bien précise pour les personnes initiées, lesquelles ne les emploient jamais indifféremment l'un de l'autre.
La manifestation la plus familière d'une force est le poids d'un corps qui correspond à l'attraction terrestre. Un ouvrier doit faire un effort musculaire (doit forcer) pour soutenir une pierre, et il sent très bien l'action de la pesanteur sur cette pierre.
Il existe d'autres sortes de forces: celle, par exemple, de la poussée sur une balle de fusil des gaz provenant de l'explosion de la poudre, ou encore celle du frottement d'une roue d'automobile qui est freinée brusquement.
Dans le SI, l'unité de force est le newton (N).
Tout objet est attiré vers la terre par une force de gravité. La valeur de cette force varie légèrement d'un endroit à l'autre sur la surface de la terre, mais, en moyenne, elle équivaut à 9,8 newtons pour 1 kilogramme.
C'est dire qu'une masse de 10 kilogrammes est attirée avec une force de 10 x 9,8 ou 98 newtons. Nous en concluons que la force de gravité à la surface terrestre est donnée par l'équation approximative:
F = 9.8m (1-1)
où
F = force de gravité (ou pesanteur), en newtons [N]
m = masse, en kilogrammes [kg]
9,8 = accélération due à la gravité [m/s2]
L'attraction gravitationnelle de la lune est environ six fois plus faible que celle de la terre, se chiffrant à 1,6 newtons pour 1 kilogramme seulement.
Sur la lune, une masse de 10 kg ne pèse plus que 10 x 1,6 ou 16 newtons, ce qui explique pourquoi les astronautes étaient capables de manipuler des charges écrasantes sans le moindre effort.
Couple
Le couple est une mesure de l'effort tournant. Il est égal au produit d'une force par la distance perpendiculaire entre l'axe de rotation et le point d'application de la force.
L'unité SI de couple est le newton-mètre (N.m).
Figure 1-1, Couple T= Fr.
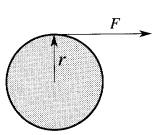
Imaginons une corde enroulée autour d'une poulie ayant un rayon r (Fig. 1-1).
Si on tire sur la corde avec une force F, la poulie aura tendance à tourner autour de son axe. Par définition, le couple est donné par l'équation:
T = Fr (1-2)
où
T = couple, en newton-mètres [N.m]
F = force, en newtons [N]
r = rayon, en mètres [m]
De cette formule nous trouvons:
F = T/r
r = T/F
Exemple 1-1
Un moteur développe un couple de démarrage de 150 N.m (T = 150).
Si la poulie a un diamètre de 1 mètre (r =diamètre / 2 = 0.5), quelle foirce de freinage (F) faut-il appliquer sur la poulie pour empêcher le moteur de tourner?
Solution
Le rayon étant de 0,5 mètre, il faudra une force F = T/r = 150 / 0.5 = 150 x 2 = 300 newtons.
Si le rayon avait été de 2 mètres, une force de 75 newtons aurait suffi.
Travail
Si on déplace un objet quelconque d'une distance den lui appliquant une force F, on effectue un travail W.
Par définition, le travail est donné par l'équation:
W = Fd (1-3)
où
W = travail, en joules [J]
F = force, en newtons [N]
d = longueur du déplacement, en mètres [m]
D'une manière générale, le travail accompli est égal au produit de la force par le chemin parcouru (dans la direction de la force).
L'unité SI de travail est le joule; il est égal au travail effectué par une force de 1 newton sur une distance de 1 mètre.
Imaginons un treuil (Fig. 1-2) levant une masse de 50 kilogrammes.
Figure 1-2 Travail W = Fd.
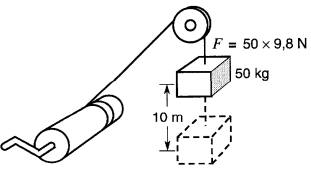
Si le treuil est actionné à la main, il faudra qu'un ouvrier déploie une certaine activité pour faire monter la masse à une hauteur déterminée. Cette activité, ou travail, se mesure par le produit de la force par la hauteur dont on a élevé la masse.
Si la masse est élevée d'une hauteur de 10 mètres, le travail sera :
W = Fd = 9,8 x 50 x 10 = 4900 joules = 4900 J
Remarquons que le couple et le travail sont tous deux obtenus en multipliant une force par une distance.
Il ne faut cependant pas confondre les termes travail et couple.
Un travail est toujours accompagné d'un mouvement ou déplacement quelconque où la force et la distance sont dans le même sens.
Par contre, le couple est simplement un effort tournant, obtenu par l'action d'une force à une certaine distance de l'axe de rotation, la force et la distance étant perpendiculaires.
Un couple peut exister même lorsqu'il n'en résulte aucun mouvement. Un travail ne peut exister sans mouvement.
Puissance
À la section ci-haut, il n'a pas été question du temps pris par l'ouvrier pour faire monter la masse de 50 kg.
Il est aisé de se rendre compte qu'il lui est plus facile d'élever la masse de 10 mètres en 10 minutes que de la faire monter à la même hauteur en 1 minute seulement.
Le travail dépensé sera toutefois le même dans les deux cas. On dira alors que la puissance mise enjeu est dix fois plus grande dans le deuxième cas.
On définit la puissance comme étant la quantité de travail accompli par seconde.
Plus une machine exécute un travail rapidement, plus elle est puissante. Inversement, le produit de la puissance par le temps nous donne le travail.
On finit toujours par terminer un travail, même avec une faible puissance, si on y met le temps voulu.
D'après ce qui a été dit plus haut, la puissance est définie par l'équation:
P = W/t
où P = puissance, en watts [W] W = travail effectué, en joules [J] t = temps, en secondes [s] L'unité SI de puissance mécanique est le watt ; il est égal à 1 joule par seconde. On utilise aussi fréquemment un multiple du watt, le kilowatt (kW), valant 1000 watts. Le horsepower (hp) est une unité anglaise de puissance qu'on utilise parfois pour exprimer la puissance d'un moteur. Elle est équivalente à 746 watts et correspond sensiblement à la puissance moyenne d'un cheval.
De même, le cheval-vapeur (ch) est une unité française de puissance; elle équivaut à 735,5 W.
Exemple 1-2
Un moteur électrique actionne un monte-charge qui élève une masse de 500 kilogrammes d'une hauteur de 30 mètres en 12 secondes (voir Fige. 1-3).
Figure 1-3 Puissance P = W/t.
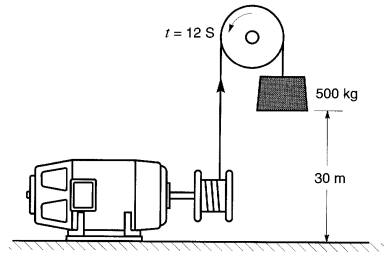
Calculer la puissance du moteur en kW. en hp et en ch.
Solution
La tension dans le câble est: F = 9,8 x 500 kg = 4900 newtons
Le travail effectué est donc:
W = Fd = 4900 x 30 = 147 000 joules
d'où la puissance P = W/t = = 147 000 / 12 = 12 250 W = 12,25 kW
la puissance en horsepower = 12 250 / 746 = 16,4 hp
la puissance en chevaux = 12 250 / 735.5 = 16,7 ch
Puissance d'un moteur
La puissance mécanique d'un moteur dépend du couple qu'il développe et de sa vitesse de rotation.
La puissance P est calculée d'après la formule de base:
P = ωT (1-5a)
où
P = puissance mécanique, en watts [W]
w = vitesse angulaire, en radians par seconde [1/s]
T = couple en newton-mètres [N.m]
Une autre formule, dérivée de la formule (1-5a) est particulièrement utile lorsque la vitesse de rotation est exprimée en tours par minute :
P = nT / 9,55
où
P = puissance
mécanique, en watts [W]
T = couple, en newtons-mètres [N.m]
n = vitesse de rotation, en tours par minute [r/min]
9,55 = facteur tenant compte des unités [valeur exacte = 30/π]
Pour mesurer la puissance d'un moteur, on peut utiliser un frein de Prony qui est composé d'une courroie et de deux pesons à ressort D1 et D2 (Fig. 1-4).
Figure 1-4 Frein de Prony
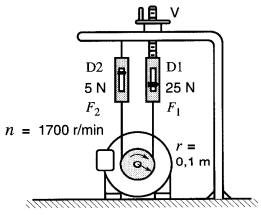
La courroie est tenue serrée sur la poulie par la vis V.
Quand le moteur n'est pas en marche, les deux pesons donnent la même lecture et l'effort tournant sur la poulie est nul.
Cependant, quand le moteur tourne dans le sens horaire, comme dans la Fig. 1-4, la force indiquée par D1 dépasse celle indiquée par D2.
Sous l'action des deux forces F1 et F2, la poulie de rayon r est soumise à deux couples F1r et F2r agissant en sens inverses.
Le couple net développé sera:
T = (F1 - F2) X r newton-mètres
Si on connaît la vitesse de rotation n, on peut en déduire la puissance du moteur.
Exemple 1-3
un essai de frein de Prony est fait sur un moteur électrique.
Les pesons indiquent respectivement des forces de 25 N et de 5 N.
Le moteur tourne à 1700 r/min et le rayon de la poulie est de 0.1 m.
Calculer le couple et la puissance développés par le moteur.
Solution
Le couple T du moteur = (25 - 5) x 0,1 = 2 N.m
d'où la puissance
P = nT / 9,55 = 1700 x 2 / 9,55 = 356 watts
La puissance est de 356 W, soit 0,48 hp environ.
Noter que cette puissance est entièrement convertie en chaleur par le frottement de la courroie sur la poulie.
Afin que la température de la poulie ne devienne pas trop élevée, il est parfois nécessaire de la refroidir par une circulation d'eau.
Il est possible d'augmenter la puissance mécanique développée par le moteur en serrant la courroie davantage.
