Notions de mécanique suite

Voir aussi

Notions de mécanique et de thermodynamique

Électrotechnique

Énergie dans les corps en mouvement

Une pierre qui tombe, une automobile qui file sur la route, un volant qui tourne, sont tous doués d'une propriété qui leur permet de faire du travail.

Le travail s'effectue lorsque le corps en mouvement est ralenti ou arrêté par un obstacle ou un frein quelconque.

On dit que ces corps en mouvement possèdent une énergie cinétique W.

Si le corps se déplace en ligne droite l'énergie cinétique est donnée par la formule :

W = mv² / 2

où

W = énergie cinétique, en joules [J]

m = masse, en kilogrammes [kg]

v = vitesse, en mètres par seconde [m/s]

Exemple 1-4

Une automobile de 2000 kg se déplace à une vitesse de 100 km/h.

Calculer son énergie cinétique W.

Solution

Une vitesse de 100 km/h correspond à:

v = 100 000 m/3600 s = 27,8 m/s

E = mv² / 2 = (2000 x 27,8²) / 2 = 72 840 joules

Un corps tournant autour d'un axe possède aussi de l'énergie cinétique dont la valeur dépend de la vitesse de rotation, de la masse du corps, et de sa forme géométrique.

L'énergie est donnée par l'équation:

W = Jω² / 2  (1-7a)

où

W = énergie cinétique, en joules [J]

J = moment d'inertie, en kilogramme-mètre carré [kg.m²]

w = vitesse de rotation, en radians par seconde [rad/s]

Une autre équation, dérivée de l'équation (1-7a), est particulièrement utile lorsque la vitesse de rotation est exprimée en tours par minute:

W = 5,48 x 10^-3Jn²

où

W = énergie cinétique, en joules [J]

J = moment d'inertie, en kilogramme-mètre carrés [kg-m²]

n = vitesse de rotation, en tours par minute [r/min]

5,48 x 10-3 = facteur tenant compte des unités [valeur exacte = (π)²/1800].

Nous verrons à la section ci-dessous (Calcul du moment d'inertie et de l'énergie cinétique de rotation) comment calculer le moment d'inertie, et dès lors, l'énergie dans le corps.

Énergie dans les corps immobiles

Même à l'état de repos, la matière a la propriété de pouvoir produire du travail.

L'eau emmagasinée derrière un barrage peut, en tombant, effectuer un certain travail ; un ressort tendu peut également, en se détendant, accomplir un travail.

L'énergie ainsi emmagasinée dans un corps immobile s'appelle énergie potentielle; elle aussi se mesure en joules.

Remarquons que l'énergie du ressort et celle de l'eau derrière un barrage peuvent être conservées indéfiniment, jusqu'à ce qu'on permette au ressort de se détendre et à l'eau de s'écouler.

Formes de l'énergie

Quels que soient l'état ou la forme sous lesquels se présente l'énergie, elle est toujours susceptible de se transformer en travail. L'énergie et le travail peuvent donc s'exprimer par la même unité, soit le joule.

L'énergie se présente sous plusieurs formes, dont voici les plus familières:

a) L'eau d'une chute, en tombant, peut faire tourner une turbine et produire de l'énergie mécanique.

b) La chaleur qui, transmise à l'eau d'un récipient, fait soulever le couvercle de ce récipient n'est qu'une autre forme d'énergie, l'énergie thermique.

c) L'explosion de la dynamite qui ébranle des blocs de granit est une manifestation de l'énergie chimique.

d) L'électricité produite par les génératrices et qui fait briller des lampes à incandescence n'est qu'une autre forme d'énergie, l'énergie électrique.

e) La chaleur libérée dans un réacteur atomique provient de l'énergie atomique.

Toutes ces formes d'énergie mécanique, électrique, chimique, atomique et thermique sont exprimées par la même unité SI, le joule (J).

Transformation de l'énergie

L'énergie présente sous une forme quelconque peut être transformée en une autre forme à l'aide de machines.

On voit comment (Fig. 1-6) l'énergie chimique du charbon et de l'air se transforme, par combustion, en chaleur (énergie thermique) en utilisant une chaudière.

Figure 1-6 La conversion de l'énergie d'une forme à une autre est effectuée au moyen de machines.

Cette chaleur fait tourner la turbine à vapeur et se transforme en énergie mécanique. Enfin, la turbine peut entraîner une génératrice et produire de l'énergie électrique.

Dans cet exemple, la chaudière, la turbine et la génératrice sont les machines qui effectuent la transformation d'énergie.

L'énergie électrique à son tour, peut servir à des fins multiples.

Par exemple, elle peut faire tourner les moteurs d'une usine (énergie mécanique), chauffer les maisons (énergie thermique), décomposer certains minerais pour libérer l'aluminium pur (énergie chimique).

Principe de la conservation de l'énergie

Chaque fois que l'énergie passe d'une forme à une autre, on constate que la quantité d'énergie totale après la transformation demeure la même.

L'énergie se transforme tout simplement; elle ne peut être ni créée, ni détruite.

Cependant, quand on passe d'une forme d'énergie à une autre, au moyen d'une machine quelconque, toute l'énergie recueillie n'est pas toujours utilisable pratiquement.

Par exemple, l'énergie thermique produite dans un moteur d'automobile servira en grande partie à chauffer inutilement les fumées d'échappement évacuées dans l'atmosphère.

De plus, une partie de l'énergie mécanique développée par le moteur est dépensée pour vaincre la résistance de l'air et les frottements des engrenages, paliers, etc.

À cause de ces pertes, l'énergie utile est inférieure à l'énergie fournie.

Rendement d'une machine

Le rendement d'une machine est donné par le rapport:

rendement = énergie utilisable  / énergie fournie à la machine = W2 /  W1

Dans cette expression, l'énergie utilisable équivaut au produit de la puissance utilisable par le temps et l'énergie fournie équivaut au produit de la puissance fournie par le temps.

Pour une transformation d'énergie donnée, le temps est le même.

Alors, on peut écrire:

rendement = puissance utilisable / puissance fournie

soit

η = P2 / P1

Pour une transformation de l'énergie thermique (chaleur) en énergie mécanique, le rendement est très faible.

Les rendements sont, pour une turbine à vapeur, de 25 % à 40 % et pour un moteur à explosion (moteur d'automobile, moteur diésel) de 15 % à 30 %.

Pour mieux apprécier l'importance de ces rendements, il est bon de prendre conscience qu'un moteur thermique qui possède un rendement de 20 % occasionne des pertes de 80 %.

C'est-à-dire que si une quantité de combustible libère 100 000 joules en brûlant, on récupère 20 000 joules en énergie mécanique et 80 000 joules sont perdus en chaleur dans l'atmosphère.

Les pertes sont données par : pertes = P1 - P2.

Le rendement des machines qui convertissent l'énergie électrique en énergie mécanique est très supérieur puisqu'il va de 80 % à 98 %, selon la grosseur de la machine.

Exemple 1-5

Calculer le rendement d'un moteur électrique qui absorbe une puissance de 10 kW et dont les pertes, à pleine charge, sont de 1 kW.

Solution

Puissance fournie = P1 = 10 kW

Pertes = P1 - P2 = 1 kW

Puissance utilisable = P2 = 9 kW

Le rendement est alors η = P1 / P2 = 9 kW /10 kW = 0,90 ou 90 %

Noter que toutes les pertes dans le moteur se retrouvent sous forme de chaleur. Dans certains cas, cette chaleur peut surchauffer et détériorer plus rapidement les bobinages.

Sources d'énergie primaire

Pour subvenir à nos besoins, nous avons recours à plusieurs sources d'énergie primaire.

La plus grande provient de l'énergie chimique contenue dans le pétrole, le charbon et le gaz naturel. Lorsque ces matériaux brûlent, ils libèrent de grandes quantités d'énergie thermique que l'on peut transformer en d'autres formes suivant les besoins.

L'eau derrière les barrages est une importante source d'énergie primaire mécanique mais, au niveau mondial, elle représente moins de 1 % des sources d'énergie chimique.

Le vent est une source d'énergie mécanique qui est de plus en plus exploitée.

Comme source d'énergie primaire électrique, on pourrait penser aux éclairs.

Cependant, même si l'on pouvait domestiquer cette source d'énergie, ce qui est peu probable, l'énergie disponible ne pourrait jamais subvenir à nos besoins.

L'énergie atomique pourra sans doute pourvoir à tous nos besoins dans l'avenir; il reste à résoudre, en particulier, le problème de l'élimination des déchets radioactifs.

L'origine de toute notre énergie (sauf l'énergie atomique) est le soleil; c'est grâce à lui que nous disposons aujourd'hui des combustibles fossiles que sont le charbon, le pétrole et le gaz naturel.

Le soleil est une source d'énergie thermique sans pareil ; chaque jour il inonde la terre d'une énergie des milliers de fois supérieure à celle que nous utilisons pour alimenter nos avions, nos trains, nos voitures, nos industries et nos maisons.

Si l'on pouvait un jour domestiquer cette source d'énergie de façon économique, le soleil pourrait subvenir à nos besoins pour des millénaires.

Quelle est la quantité d'énergie contenue dans ces diverses sources d'énergie primaire?

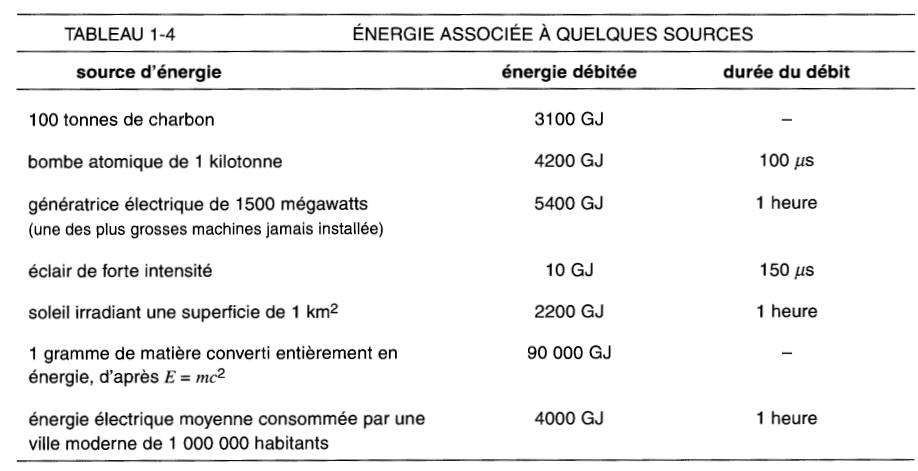
Le tableau 1-3 nous donne une idée de l'énergie thermique libérée par les produits chimiques tandis que le tableau 1-4 établit une comparaison avec les autres sources d'énergie.

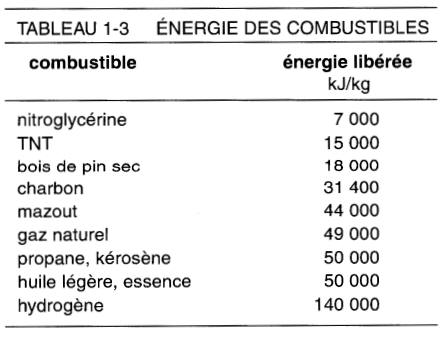
On peut être surpris de constater que les explosifs (TNT, nitroglycérine) emmagasinent moins d'énergie par kilogramme que le charbon; ces produits semblent en contenir plus parce qu'ils brûlent avec une rapidité effarante lorsqu'on les allume.

À cause de cela, les explosifs développent des puissances énormes; c'est pourquoi on les utilise pour les travaux de démolition.

Le tableau 1-4 fait ressortir le fait qu'une grosse génératrice électrique débite en une heure une quantité d'énergie équivalent à celle d'une bombe atomique de 1 kilotonne.

Cette énergie correspond sensiblement à la consommation horaire d'une ville moderne de 1 million d'habitants.

Calcul du moment d'inertie et de l'énergie cinétique de rotation

Tout corps tournant autour d'un axe s'oppose à un changement de sa vitesse. Cette propriété est caractérisée par son inertie, appelée plus correctement moment d'inertie J.

Le moment d'inertie dépend de la masse et de la forme du corps tournant.

Connaissant le moment d'inertie J du corps, il est facile de calculer l'énergie cinétique qu'il possède à une vitesse donnée.

De plus, la valeur de J permet d'estimer le temps nécessaire pour amener une machine à sa vitesse finale ou pour l'arrêter.

L'unité SI de moment d'inertie est le kilogramme-mètre carré [kg.m²].

Le tableau 1-5 donne les formules permettant de calculer le moment d'inertie de quelques corps de forme simple.

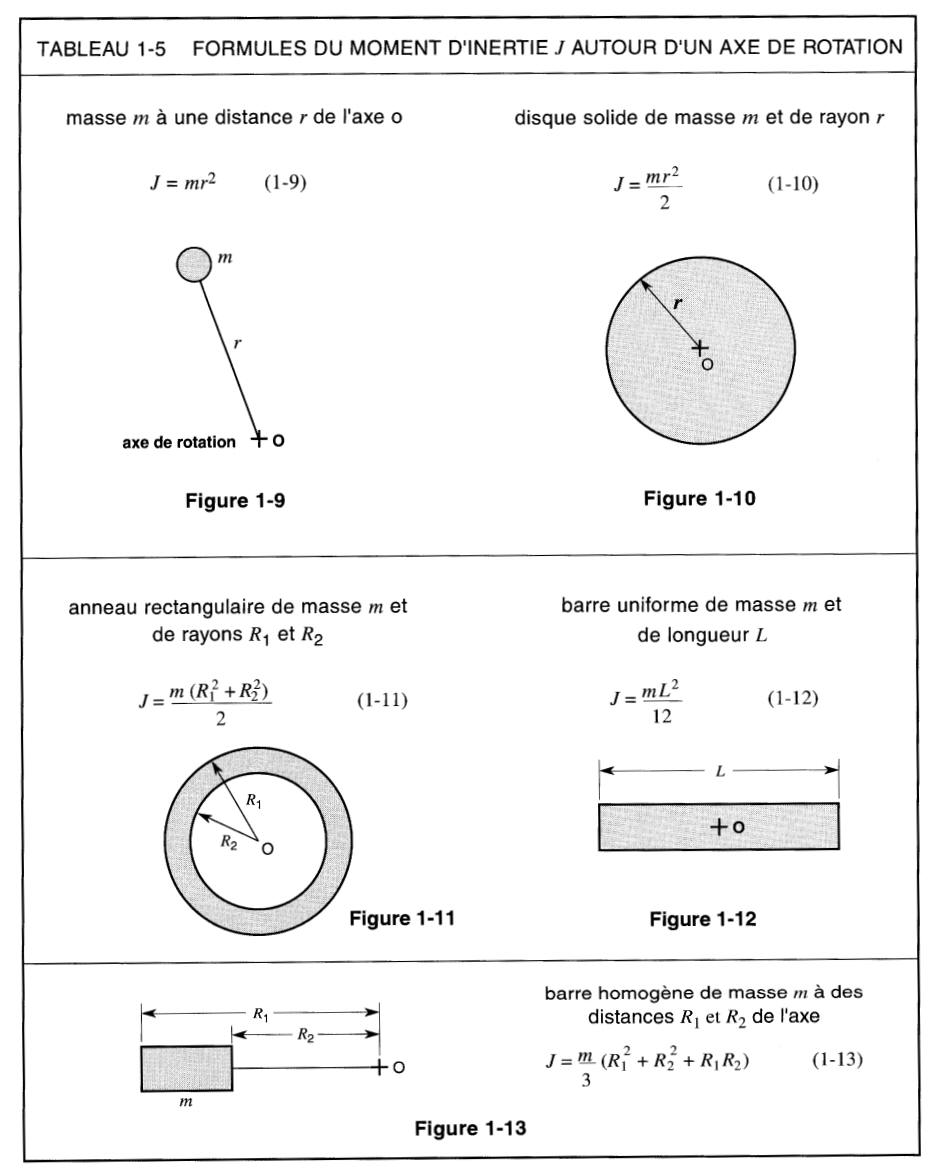
Si le corps possède une forme plus complexe, on peut le subdiviser en morceaux ayant les formes simples illustrées dans ce tableau.

Comme le moment d'inertie total d'un corps est égal à la somme de ses moments d'inertie individuels, on peut trouver la valeur de J pour des corps de formes assez variées.

L'inertie joue un rôle important dans les machines rotatives; par conséquent il est utile d'en donner quelques exemples.

Exemple 1-6

Un volant solide en acier a un diamètre de 1 m et une épaisseur de 225 mm (Fig. 1-7).

Si sa masse est de 1400 kg calculer :

a) son moment d'inertie

b) l'énergie cinétique lorsque le volant tourne à 1800 r/min

Figure 1-7

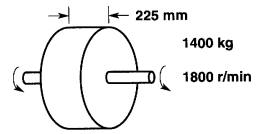
Solution

a) En se référant au tableau 1-5, équation (1-10), le moment d'inertie est :

J = mr² / 2 = 1400 x 0,5² / 2 = 175 kgm²

b) l'énergie cinétique est :

W = 5,48 x 10^-3Jn² (éq. 1-7b)

= 5,48 x 10^-3 x 175 x (1800)² = 3,1 MJ

Exemple 1-7

Un volant avant la forme donnée à la Fig. 1-13 est composé d'un anneau de 80 kg et d'un moyeu droit de 20 kg.

Calculer la valeur de son moment d'inertie.

Figure 1-13 Voir exemples 1-7 et 1-9.

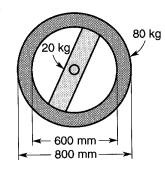
Solution

Pour l'anneau, la valeur de J est donnée par l'équation (1-11):

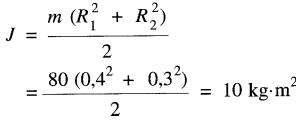
Pour le moyeu droit la valeur de J est donnée par l'équation (1-12):

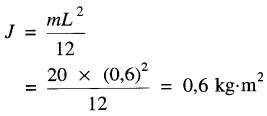
Le moment d'inertie total du volant vaut donc :

J = 10 + 0,6 = 10,6 kg.m²

Exemple 1-8

Calculer l'énergie emmagasinée dans le volant de la Fig.1-13 à 60 r/min et 600 r/min.

Solution

a) à 60 r/min, l'énergie emmagasinée est:

W = 5,48 x 10^-3 x 10,6 x (60)² = 209 joules

b) pour une vitesse de 600 r/min, soit 10 fois plus grande qu'auparavant, l'énergie augmente non pas de 10 fois, mais de 100 fois :

W = 20 900 J = 20,9 kJ

Couple, inertie et variation de vitesse

Pour changer la vitesse de rotation d'un corps, il faut lui appliquer un couple. Plus ce couple est élevé, plus la vitesse augmente rapidement.

D'autre part, pour un couple donné, la vitesse d'un corps massif (possédant un grand moment d'inertie) change plus lentement que celle d'un corps léger.

Le seul fait d'appliquer un couple ne suffit pas à faire croître la vitesse de rotation d'un corps; on doit également y mettre du temps.

C'est seulement en appliquant un couple T pendant un temps Δt que l'on réussit à changer la vitesse de rotation.

Une expression très simple relie ces divers facteurs:

Δn = 9.55TΔt / J

où

Δn = variation de vitesse, en tours par minute [r/min]

T = couple en newton-mètre [N.m]

Δt = temps d'application du couple, en seconde [s]

J = moment d'inertie, en kilogramme-mètre carré [kg.m2]

9,55 = facteur tenant compte des unités [valeur exacte = 30/π]

Si le couple agit dans le même sens que la rotation, la vitesse augmente. Par contre, si le couple agit dans le sens contraire de la rotation, la vitesse diminue.

La valeur Δn peut donc représenter une augmentation ou une diminution de vitesse.

Exemple 1-9

Le volant de la Fig. 1-8 tourne à 60 r/min. On désire porter sa vitesse à 600 rh/min en lui appliquant un couple constant de 20 N.m. Calculer le temps requis.

Solution

La variation de vitesse est :

Δn = (600 - 60) = 540 r/min

Le moment d'inertie est:

J = 10,6 kg-m²

On a donc:

Δn = 9,55 TΔt / J

soit

540 = 9,55 x 20 x Δt / 10,6

d'où

Δt = 30 secondes

Vitesse de rotation et charge d'un moteur

Lorsqu'un moteur électrique entraîne une charge mécanique, on a un système régi par trois facteurs :

le couple développé par le moteur, le couple exercé par la charge, et la vitesse de rotation.

Nous expliquons maintenant comment ils sont reliés.

Considérons une charge couplée à un moteur par l'entremise d'un essieu (Fig. 1-14).

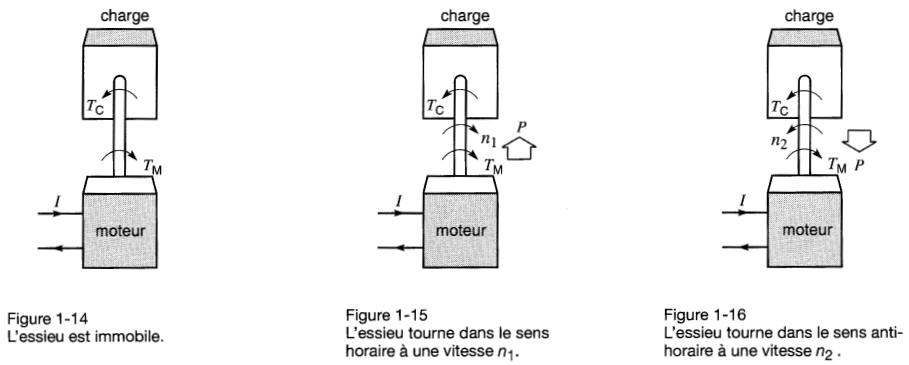
La charge exerce un couple constant TC qui agit dans le sens antihoraire.

D'autre part, le couple TM développé par le moteur agit dans le sens horaire. De plus, on suppose que l'on peut faire varier le couple en augmentant ou en diminuant le courant I circulant dans le moteur.

Supposons que le système soit initialement au repos et que TM = TC.

Puisque les couples sont égaux et agissent en sens contraires, le couple résultant est nul; par conséquent, l'essieu n'a aucune tendance à tourner.

À cause des couples opposés, l'essieu subit une certaine déformation due à la torsion, mais à part cela, rien ne se produit.

 Supposons que l'on veuille faire tourner la charge dans le sens horaire à une vitesse n1. Pour ce faire, on doit augmenter le courant I, afin que TM devienne supérieur à Tc.

Le couple net sur l'essieu agit dans le sens horaire. La vitesse augmente progressivement mais dès qu'elle atteint la valeur nt, on réduit le courant afin que TM soit de nouveau exactement égal à TC.

Le couple net sur le système est de nouveau nul et la vitesse nt n'a dorénavant aucune tendance à augmenter ni à diminuer (Fig. 1-15).

Ceci nous amène à une conclusion très importante.

La vitesse de rotation d'une charge demeure fixe lorsque le couple TM développé par le moteur est égal et opposé au couple TC exercé par la charge.

De prime abord, il est difficile d'accepter cette conclusion, parce qu'on est porté à croire que le système s'arrêtera tout simplement lorsque TM = TC.

Mais tel n'est pas le cas. Le système composé du moteur et de sa charge reste plutôt dans une condition d'équilibre dynamique car le couple net est nul.

Le système tournant maintenant dans le sens horaire à une vitesse n1, supposons que l'on réduise TM afin qu'il soit inférieur à TC. Le couple net sur l'essieu agit maintenant dans le sens antihoraire.

Par conséquent, tant que TC excède TM la vitesse diminue progressivement.

Si cette condition subsiste assez longtemps, la vitesse deviendra finalement nulle, après quoi le moteur se mettra à tourner en sens inverse.

Si l'on ajuste le couple du moteur de sorte que TM = TC au moment où la vitesse inverse atteint la valeur n2, le système tournera indéfiniment à cette nouvelle vitesse (Fig. 1-16).

Noter que dans les figures 1-14, 1-15 et 1-16, les trois couples TM de même que les trois couples TC sont identiques, même si l'essieu est immobile ou si le sens de rotation est horaire ou antihoraire. Dès que les couples TM et TC ne sont plus égaux et opposés, la vitesse se met à changer.

Le taux de changement de la vitesse dépend de l'inertie des parties tournantes, aspect que nous traitons davantage à la section Changement de vitesse d'un moteur entraînant une charge ci-dessous.

Échange de puissance mécanique dans un système d'entraînement

Considérons le cas de la Fig. 1-15; on observe que le couple du moteur TM agit dans le même sens (horaire) que la vitesse n1.

 Cela indique que le moteur fournit de la puissance mécanique à l'essieu.

Par contre, le couple exercé par la charge agit en sens inverse de la vitesse n1.

Par conséquent, la charge reçoit de la puissance mécanique de l'essieu.

On peut alors énoncer la règle générale suivante:

Lorsque le couple développé par un moteur agit dans le même sens que la rotation, le moteur fournit de la puissance mécanique à la charge.

Dans le cas contraire, le moteur reçoit de la puissance de la charge.

Par exemple, dans le cas de la Fig. 1-16, le moteur reçoit de la puissance de la charge parce que TM et n2 agissent en sens contraires.

Bien que cette condition soit inhabituelle, elle se produit pendant de courtes périodes dans plusieurs systèmes d'entraînement, notamment dans les locomotives électriques.

Changement de vitesse d'un moteur entraînant une charge

Lorsqu'un moteur entraîne une charge, la vitesse est habituellement stable. Dans cet état d'équilibre dynamique, le couple TM développé par le moteur est égal au couple Tc requis par la charge.

Cependant, comme on vient de le voir, si le couple du moteur est supérieur à celui imposé par la charge, la vitesse augmente.

 Inversement, lorsque le couple du moteur est inférieur à celui de la charge, la vitesse diminue.

L'augmentation ou la diminution de vitesse Δn est encore donnée par l'équation (1-14), sauf que le couple T est remplacé par le couple résultant (TM - Tc) du système, soit:

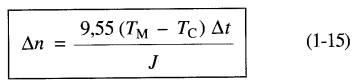
où

Δn = changement de la vitesse de rotation [r/min]

TM = couple du moteur [N.m]

TC = couple exercé par la charge [N.m]

Δt = intervalle durant lequel les couples TM et Tc sont appliqués [s]

J = moment d'inertie de toutes les parties tournantes [kg-m²]

Moteurs et entraînements linéaires

Les charges rotatives comme les ventilateurs et les pompes centrifuges sont bien adaptées pour l'accouplement direct avec des moteurs.

Cependant, les charges qui se déplacent linéairement comme les grues, les trains, etc., doivent être munies d'un «convertisseur de mouvement» pour transmettre la puissance provenant d'un moteur tournant.

Le convertisseur de mouvement peut être constitué d'une poulie et d'une corde, ou simplement d'une roue qui se déplace sur un rail.

Ces convertisseurs sont tellement simples que l'on ignore souvent le rôle important qu'ils jouent. Le mouvement linéaire est caractérisé par une vitesse linéaire v et une force F.

Pour le mouvement rotatif, les grandeurs équivalentes sont la vitesse de rotation n et le couple T.

Quelle est la relation entre ces grandeurs dans le cas d'un convertisseur de mouvement ?

Considérons le pont de levage de la Fig. 1-17.

Figure 1-17
Conversion d'un mouvement rotationnel en mouvement rectiligne.

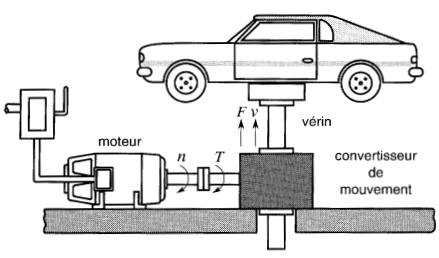
Le moteur produit un couple T et tourne à une vitesse n. Le vérin se déplace à une vitesse v, tout en exerçant une force F.

La puissance P2 utilisée pour lever la charge est:

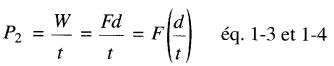
d'où P₂ = vF

D'autre part, la puissance Pl développée par le moteur est

P₁ = nT / 9,55  éq. 1-5b

Si on néglige les pertes dans le convertisseur de mouvement, on obtient:

P₂ = P₁

Par conséquent, pour un convertisseur parfait:

nT = 9,55 vF  (1-16)

ou

n = vitesse de rotation [r/min]

T = couple [N.m]

F = force linéaire [N]

v = vitesse linéaire [m/s]

9,55 = facteur tenant compte des unités [valeur exacte = 30/π]

Exemple 1-10

Le pont de la Fig. 1-17 doit soulever une voiture de 1400 kg à une vitesse de 1,5 m/min.

Si le moteur électrique tourne à 1800 r/min, calculer le couple et la puissance du moteur. Négliger les pertes.

Solution
La force de gravité sur la voiture est:

F = 9,8m = 9,8 x 1400 = 13 720 N

En utilisant l'équation (1-16), on trouve le couple T:

nT = 9,55vF

1800 T = 9,55 x 1,5 m / 60s x 13 720

T = 1,82 N.m

La puissance du moteur est :

p = nT / 9,55 = 1800 x 1,82 / 9,55 = 343 W