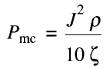 (29-1)
(29-1)
Pertes, échauffement et rendement des machines électriques
Nous avons déjà vu à la section Notions de mécanique et Thermodynamique que la transformation de l'énergie d'une forme en une autre au moyen d'une machine s'accompagne toujours d'une certaine perte de puissance. Cette perte se produit dans la machine elle-même et donne lieu:
1. à un échauffement des différentes parties de la machine;
2. à une diminution du rendement de la machine, la puissance débitée par la machine étant inférieure à la puissance qui lui est fournie.
L'étude des phénomènes occasionnant des pertes de puissance est d'un grand intérêt, car elle nous révèle comment ces pertes peuvent être réduites.
Dans cette section, nous analysons les pertes dans les machines à c.c., mais les mêmes remarques s'appliquent à la plupart des machines à courant alternatif.
Les machines électriques peuvent être classées en deux groupes: celles qui comprennent des parties tournantes (moteurs, génératrices) et celles qui n'en ont pas (transformateurs, réactances).
Des pertes électriques et mécaniques sont produites dans les machines tournantes;
dans les machines fixes, seules les pertes électriques sont produites.
Pertes mécaniques
Les pertes mécaniques proviennent:
1. du frottement dans les paliers ;
2. du frottement des balais sur le collecteur ou sur les bagues;
3. du frottement de l'air sur l'induit et sur le ventilateur destiné au refroidissement de la machine.
Les pertes qui proviennent du frottement du rotor sur des organes fixes (paliers, balais) contribuent à l'échauffement de la machine. Plus la machine tourne vite, plus les pertes mécaniques deviennent importantes.
Ces pertes dépendent de nombreux facteurs et il est très difficile de prédire leur valeur. Pour les déterminer avec exactitude, il faut faire des essais sur la machine.
Pertes électriques dans les conducteurs
Les pertes électriques sont divisées en deux catégories: les pertes dans les conducteurs et les pertes dans le fer. Dans les conducteurs, elles sont dues à l'effet Joule.
Elles s'expriment par la formule P = RI², où I est le courant qui parcourt l'enroulement de résistance R. Ces pertes se manifestent par la chaleur qui se dégage des conducteurs.
Dans le cas des moteurs et des génératrices, les pertes ont lieu dans l'enroulement de l'induit, dans les enroulements inducteurs (shunt et série), dans les balais, dans le rhéostat d'excitation et dans l'enroulement des pôles de commutation.
Au lieu d'utiliser la formule P = RI², il est parfois plus commode de calculer les pertes d'après la masse des conducteurs.
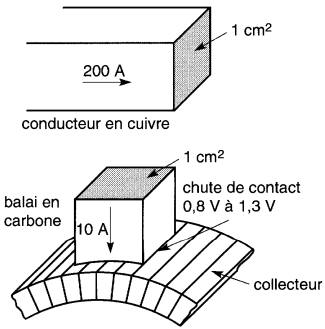
Les pertes massiques sont donnés par la formule:
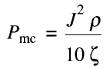 (29-1)
(29-1)
où
Pmc = pertes massiques des conducteurs [W/kg]
J = densité de courant dans les conducteurs [A/cm2]
ρ = résistivité du conducteur [nQ.m]
ς = masse volumique du
conducteur [kg/m³]
10 = constante tenant compte des unités
On constate que les pertes par unité de masse sont proportionnelles au carré de la densité de courant dans le conducteur.
Comme ordre de grandeur, on utilise des densités variant de 150 A/cm² à 600 A/cm² pour les conducteurs en cuivre.
Les pertes correspondantes varient alors d'environ 5 W/kg jusqu' à 80 W/kg.
Les densités élevées requièrent un bon refroidissement pour éviter les températures excessives. La faible résistance des balais produit des pertes Joule négligeables comparativement aux pertes électriques occasionnées par la chute de tension entre le balai et le collecteur.
Cette chute varie ordinairement de 0,8 à 1,3 volts, selon le type de balai utilisé et la pression appliquée.
Dans les balais en carbone, on utilise des densités de courant beaucoup plus faibles que dans le cuivre, soit environ 10 A/cm² (Fig. 29-1).
Figure 29-1 Comparaison des densités de courant utilisées dans les conducteurs en cuivre et dans les balais
Exemple 29-1
L'induit de la Fig. 28-4 loge 243 bobines pesant chacune 0.35 kg.
Calculer les pertes Joule à une température de 120 °C pour une densité de courant (le 400 A/cm². La masse volumique du cuivre est de 8890 kg/m² et sa résistivité à 0 °C est de 15,88 nΩ.m (nanohm-mètre).
Solution
La masse totale du cuivre est:
m = 243 bobines x 0,35 kg/bobine = 85 kg
La résistivité du cuivre à 120 °C est:
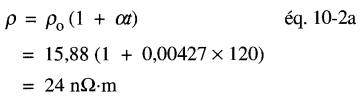
D'après l'équation 29-1, les pertes massiques sont:
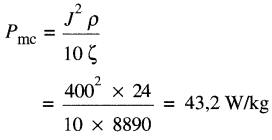
Les pertes Joule dans l'induit sont:
P = 43,2 W/kg x 85 kg = 3672 W = 3,67 kW
Pertes électriques dans le fer
Il ne se produit aucune perte dans une pièce de fer traversée par un flux qui ne change ni d'intensité, ni de direction.
Ainsi, lorsqu'un électro-aimant est excité par un courant continu, il se produit des pertes dans le cuivre de la bobine seulement; il n'y en a aucune dans le fer du noyau.
Par contre, des pertes importantes se produisent dans les parties en fer où le flux varie en grandeur ou en direction. C'est le cas du circuit magnétique des machines à courant alternatif dans lesquelles le flux est alternatif.
C'est aussi le cas de l'induit des machines à courant continu où le flux, bien que constant en intensité, change de sens périodiquement et rapidement. À noter que les pertes dans le fer d'un induit imposent un couple de freinage mécanique, tout comme les pertes par frottement sur les paliers.
Les pertes dans le fer sont attribuables au phénomène d'hystérésis et aux courants de Foucault.
1. Pertes par hystérésis.
On a vu que les pertes par hystérésis sont proportionnelles au nombre de fois où l'aimantation change de sens par seconde, donc à la vitesse de rotation des parties tournantes. Elles varient à peu près comme la densité de flux à l'exposant 1,6.
2. Pertes par courants de Foucault.
Pour expliquer les pertes par courants de Foucault, considérons un noyau cylindrique en fer qui tourne entre les pôles d'un aimant (Fig. 29-2a).
Figure 29-2 a. Tension induite dans un rotor plein ; b. Courants de Foucault résultants
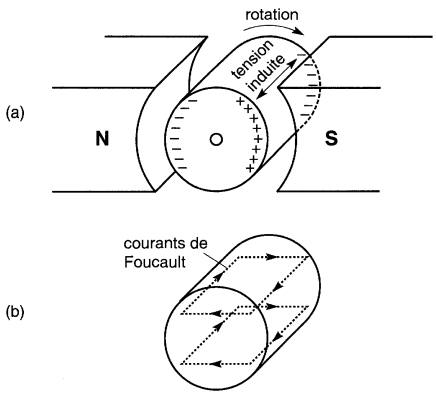
En tournant, le noyau coupe des lignes de flux et, d'après le principe III de l'électromagnétisme, une tension est induite dans le noyau même, avec les polarités indiquées. Cette tension fait circuler des courants dans la masse du noyau.
Ces courants, auxquels on donne le nom de courants de Foucault, provoquent un échauffement, par effet Joule, du noyau de fer (Fig. 29-2b). La chaleur dégagée correspond à une perte de puissance proportionnelle au carré de la vitesse de rotation et au carré de la densité de flux.
Si le noyau magnétique de l'induit des machines à courant continu était fabriqué d'un seul bloc, la chaleur produite par les courants de Foucault serait tellement grande que le noyau serait porté au rouge en peu de temps, de sorte que ces machines seraient inutilisables.
Pour minimiser les pertes par courants de Foucault, on est conduit à feuilleter le noyau de l'induit. Le noyau est alors formé d'un empilage de tôles minces, isolées les unes des autres afin d'empêcher le passage du courant d'une tôle à l'autre. Les tôles sont disposées parallèlement au sens des lignes de force (Fig. 29-3).
Figure 29-3 a. Rotor formé d'un empilage de tôles; b. Les courants de Foucault dans chaque tôle sont beaucoup moins grands que dans un rotor plein
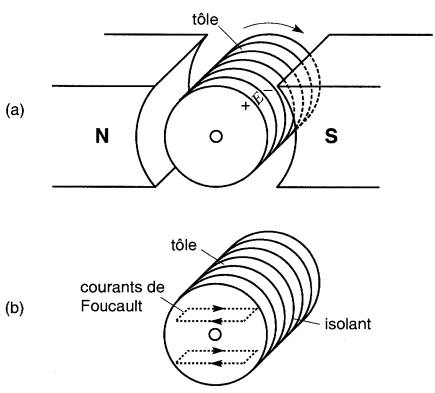
Les pertes sont atténuées davantage en augmentant la résistivité de la tôle par addition de 3 à 4 % de silicium. Avec des tôles au silicium de 0,35 mm d'épaisseur (Fig. 29-4), on peut limiter ces pertes à une petite fraction de la puissance de la machine.
Figure 29-4 Four électrique de 150 kW utilisé pour recuire les tôles magnétiques après le poinçonnage des encoches. Cette opération, effectuée à 800 °C dans une atmosphère contrôlée, réduit sensiblement les pertes massiques du fer. On voit ici les tôles sortant du four

Bien que le flux ne varie pas dans les pièces polaires des machines à courant continu, ces pièces sont généralement formées de tôles de fer doux car il est plus économique de tailler des tôles que d'usiner une grosse pièce d'acier pour lui donner la forme particulière des pièces polaires.
Comme les pertes dans le fer dépendent de plusieurs facteurs, les fabricants de tôles d'acier présentent généralement cette information sous forme de courbes.
Comme ordre de grandeur, pour une densité de 1,5 T et une fréquence de 60 Hz, les pertes totales dans la tôle de 0,35 mm (jauge n° 29), varient de 1,5 W/kg à 8 W/kg, selon la qualité de l'acier.
La Fig. 29-5 donne les pertes massiques en fonction de la densité de flux pour diverses tôles utilisées dans les induits. Ces pertes donnent la somme des pertes par hystérésis et par courants de Foucault pour une fréquence de 60 Hz.
Figure 29-5 Pertes massiques de diverses tôles utilisées dans les induits et les noyaux de transformateurs
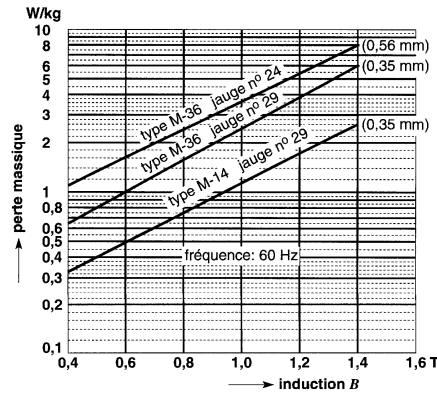
On utilise l'acier au silicium M-36 sur des induits de puissance moyenne, tandis que le type M-14 est réservé aux grosses machines à haut rendement et aux transformateurs.
On note que pour une induction donnée, la tôle mince (0,35 mm) donne des pertes massiques sensiblement inférieures à celles d'une tôle plus épaisse (0,56 mm). Cette diminution est due uniquement à la réduction des pertes par courants de Foucault.
Courants de Foucault dans un noyau stationnaire
Nous avons vu que des pertes par courants de Foucault sont produites dans un noyau métallique lorsqu'il tourne dans un champ magnétique.
Des pertes semblables sont aussi produites lorsqu'un noyau stationnaire est traversé par un flux alternatif. La Fig. 29-6a montre une plaque métallique traversée par un flux alternatif.
Figure 29-6 Un flux alternatif traversant une plaque métallique induit dans celle-ci des tensions alternatives et des courants de Foucault
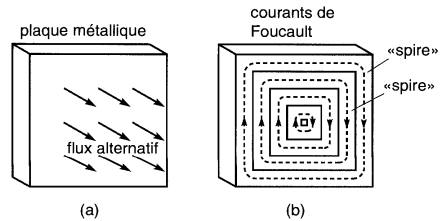
On peut considérer que la plaque est formée de plusieurs spires rectangulaires court-circuitées sur elles-mêmes.
Le flux alternatif induit une tension alternative dans chacune des «spires», produisant ainsi des courants de court-circuit alternatifs montrés à la Fig. 29-6b.
Ces courants de Foucault produisent dans la plaque métallique des pertes RI2 qui varient avec le carré de la fréquence et le carré de la densité de flux.
Or, la densité de flux circulant dans le noyau de fer d'un transformateur ou d'un moteur à courant alternatif est toujours importante, de sorte que si le noyau était plein, les courants de Foucault et les pertes résultantes seraient excessivement élevés (Fig. 29-7).
Figure 29-7 Des courants de Foucault intenses sont induits dans un noyau de fer plein
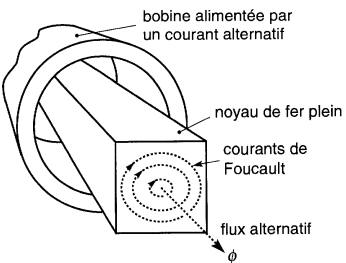
Afin de réduire les pertes, le noyau est constitué de lamelles d'acier très minces, isolées les unes des autres (Fig. 29-8).
Figure 29-8 Un noyau de fer composé de tôles minces diminue de beaucoup les pertes par courants de Foucault
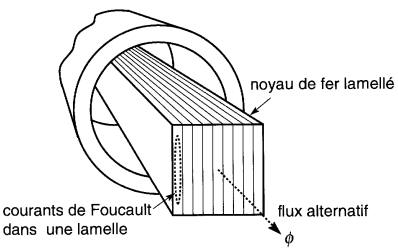
Le flux dans chaque lamelle est alors très petit et comme sa résistance est beaucoup plus élevée que celle d'un noyau plein, les courants de Foucault, de même que les pertes totales, sont réduites à une fraction de leur valeur originale.
Pour une fréquence de 60 Hz, on utilise des tôles ayant généralement une épaisseur de 0,35 mm.
Variation des pertes avec la charge
Un moteur à c.c. tournant à vide ne développe évidemment aucune puissance utile. Il faut cependant lui fournir une certaine puissance si l'on veut qu'il continue à tourner.
Cette puissance est absorbée par le frottement mécanique, la ventilation, les pertes dans le fer et les pertes dans le cuivre de l'enroulement shunt.
Les pertes dans le cuivre de l'induit, de l'inducteur série et de l'enroulement de commutation sont minimes car le courant à vide est très faible par rapport au courant nominal.
Quand la machine est chargée (mécaniquement, si c'est un moteur, et électriquement, si c'est une génératrice), et dans les bobines de commutation.
Les pertes par effet Joule dans ces enroulements augmentent donc. Par contre, les pertes dans le fer et les pertes mécaniques demeurent sensiblement les mêmes qu'à vide, à moins que la vitesse ne change de façon appréciable.
De façon générale, les pertes dans une machine sort composées de pertes constantes et de pertes variables qui augmentent avec la charge.
Puisque ces pertes se transforment en chaleur, il en résulte une élévation de température. Cette élévation de température par rapport à la température ambiante est appelé échauffement.
Puissance et capacité de surcharge
L'échauffement d'une machine dépend des pertes et on sait que ces pertes augmentent avec la charge. Puisque l'échauffement doit être limité afin de ne pas détériorer les isolants, la charge doit aussi être limitée.
En somme, dans la majorité des cas, c'est l'élévation maximum de température des isolants qui détermine la puissance maximale qu'une machine peut débiter.
Lorsqu'une machine fournit une puissance dépassant sa puissance nominale, il y a échauffement excessif et par suite, détérioration partielle de la machine, ce qui réduit inévitablement le nombre d'années de service qu'on peut en attendre.
Lorsqu'une machine fonctionne de façon intermittente, elle peut supporter, sans risque d'échauffement excessif, une surcharge d'autant plus forte que son temps d'utilisation est plus court.
Ainsi, un moteur d'une puissance nominale de 10 kW peut facilement supporter une charge de 15 kW s'il ne fonctionne que quelques minutes par heure.
Toutefois, à des valeurs plus élevées, sa capacité de surcharge est limitée par d'autres facteurs, principalement électriques. Par exemple, il est impossible pour une machine de 10 kW de débiter une puissance de 100 kW.
Courbe de rendement
Le rendement d'une machine est le rapport entre la puissance utile P2 et la puissance Pi fournie à la machine (voir Notions de mécanique).
La puissance fournie est égale à la somme de la puissance utile et des pertes p.
On a alors:
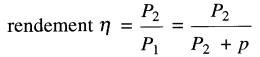 (29-2)
(29-2)
Le rendement varie donc avec la puissance utile et les pertes; la relation entre le rendement et la puissance utile est généralement donnée par un graphique.
L' exercice numérique suivant indique la marche à suivre pour le calcul du rendement d'un moteur à courant continu.
Exemple 29-2
Un moteur compound à C.C. de 10 kW. 1150 r/min, 230V 50A a les pertes suivantes à pleine charte:
pertes par frottement sur les paliers 40 W
pertes par frottement des balais 50 W
pertes par ventilation = 200 W
pertes mécaniques totales 290 W (1)
pertes Joule dans le champ shunt = 120 W (2)
pertes dans le fer de l'induit = 420 W (3)
Total des pertes constantes = 830 W (4)
pertes Joule à pleine charge dans :
a) l'induit = 500 W
b)
le champ série 25 W
c) l'enroulement de commutation 70 W
Total des pertes variables 595 W (5)
a) Évaluer les pertes et le rendement à vide, ainsi qu'à 25%, 50%, 75%, 100$ et 150% de la charge nominale de la machine. (On négligera les pertes dues à la chute de tension entre les balais et la surface du collecteur.)
b) Tracer la courbe du rendement en fonction de la charge.
Solution
a) Fonctionnement à vide.
Les pertes à vide sont données par la somme des pertes mécaniques (1), des pertes dans le champ shunt (2) et des pertes dans le fer (3):
pertes à vide = 290 + 120 + 420 = 830 W
Ces pertes demeurent sensiblement constantes, même quand la charge varie.
À vide, les pertes Joule dans le circuit de l'induit sont négligeables. Le rendement est nul à vide, car aucune puissance utile n'est développée par le moteur.
Fonctionnement en charge
Lorsque le moteur est chargé à 25 % de sa puissance nominale, le courant qu'il tire est d'environ 25 % (ou 1/4) du courant nominal.
Puisque les pertes par effet Joule varient selon le carré du courant, les pertes dans le circuit de l'induit sont:
pertes variables = (1/4)² x 595 = 37 watts
Les pertes totales à 1/4 de la charge nominale sont :
p = 37 + 830 = 867 W
La puissance utile P2 développée par la machine à 25 % de la charge nominale, exprimée en watts, est:
P2 = 10 kW x 0,25 = 2500 W
La puissance P1 absorbée par le moteur est donnée par la somme de la puissance utile et des pertes :
P1 = P2 +p = 2500 + 867 = 3367 W
Le rendement est alors:
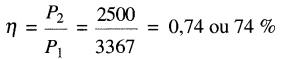
On trouvera de la même façon les pertes à 50 %, 75 %, 100 % et 150 % de la charge nominale :
A 50 %:
p = (1/2)² x 595
+ 830 = 979 W
À 75 %:
p = (3/4)² x 595 + 830 = 1165 W
À 100
%:
p = 595 + 830 = 1425 W
À 150 %:
p = (1,5)² x 595 + 830 =
2169 W
b) Les calculs du rendement à différentes valeurs de charge sont résumés dans le tableau 29-1.
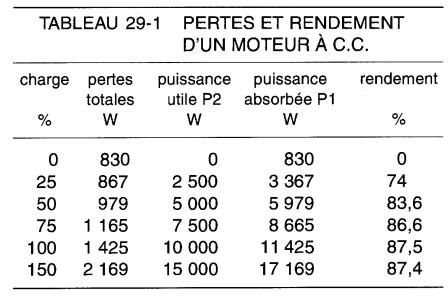
Les résultats sont représentés graphiquement à la Fig. 29-9.
Figure 29-9 Rendement et pertes en fonction de la puissance mécanique développée
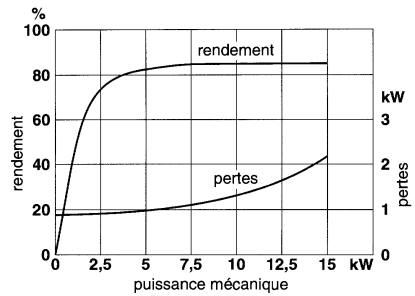
Il est bon de retenir que le rendement d'un moteur est faible aux faibles charges.
On aura donc intérêt à choisir la capacité d'un moteur destiné à entraîner une charge de valeur déterminée, de façon que la puissance nominale de ce moteur soit à peu près égale à la puissance exigée par la charge.
Normes d'échauffement
On a déjà vu à la section que les isolants sont groupés en différentes classes correspondant à la température maximale qu'ils peuvent supporter.
Ainsi, un isolant de classe 130 °C aura une durée de vie raisonnable (environ 20 000 h) si sa température n'excède pas 130 °C.
Les organismes de normalisation établissent également une température ambiante maximale dont la valeur est habituellement de 40 °C.
Cette température normalisée est établie pour les raisons suivantes :
1. elle permet aux fabricants de machines électriques de prévoir les pires conditions de température ambiante auxquelles leurs machines peuvent être soumises et, par conséquent,
2. elle permet aux mêmes fabricants de normaliser la grosseur des machines et de donner des performances garanties.
On peut mieux apprécier l'impact de cette norme quand on réalise que toutes les machines et tous les appareils électriques isolés classe 105 °C sont environ 15 % plus petits, donc moins coûteux lorsqu'on spécifie une température ambiante normalisée de 30 °C au lieu de 40 °C.
La Fig. 29-10 montre les limites de température des différentes classes d'isolants (courbe 1) et la température ambiante normalisée (courbe 3).
Figure 29-10 Normes de température utilisées pour certains moteurs à courant alternatif (tirées des publications CSA C22.2, n°S 0, 11, 54). Voir aussi le chapitre 9, tableau 9-2
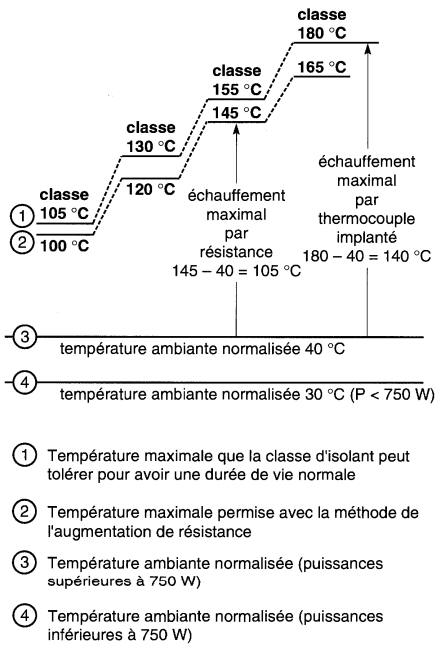
Pour chaque classe, la
différence de température entre ces deux courbes donne l'échauffement normalisé
(«hot-spot temperature rise»); c'est elle qui permet au fabricant d'établir
la grosseur de son moteur, de son relais, etc.
Par exemple, supposons que l'on désire déterminer l'échauffement d'un moteur de 100 kW, isolation classe 130 °C. Lors des essais, on devra lui appliquer une charge de 100 kW et déterminer l'endroit le plus chaud («hot-spot») à l'intérieur de la machine.
Ce point le plus chaud est probablement situé en plein milieu d'une encoche, à l'intérieur même d'une bobine, soit à un endroit tout à fait inaccessible.
Comment atteindre cet endroit critique?
Le fabricant peut implanter des petits détecteurs de température (thermocouples ou thermistors) à l'intérieur des bobines, permettant de déterminer la température crête lorsque la machine est en marche.
Cependant, cette méthode directe de mesure de la température du point le plus chaud «hot-spot» est coûteuse et elle n'est justifiable que pour les machines de grande capacité.
C'est pourquoi les bureaux de normalisation comme le CSA (Association canadienne de normalisation) permettent l'utilisation d'une deuxième méthode pour mesurer la température.
Comme nous allons l'expliquer, elle consiste à mesurer l'augmentation de résistance d'un enroulement, et à en déduire la température. Cette température représente la température moyenne de l'enroulement. Elle est évidemment plus basse que celle que donnerait un détecteur implanté.
Il a donc fallu définir une autre norme : on suppose que l'écart entre la température maximale réelle et la température déterminée par la méthode de l'augmentation de résistance est, soit 5 °C, soit 10 °C, soit 15 °C
Habituellement, l'écart dépend de la classe d'isolant. La courbe 2 donne la température maximale permise des enroulements d'un moteur à courant alternatif lorsqu'on utilise la méthode de l'augmentation de résistance.
On constate que l'écart entre cette courbe et la courbe 1 est de:
5 °C pour l'isolation classe 105 °C,
10 °C pour les classes 130 °C et 155 °C,
15 °C pour la classe 180 °C.
Il s'ensuit que l'échauffement permis lorsqu'on utilise la méthode de l'augmentation de résistance est de :
60 °C pour l'isolation classe 105 °C,
80 °C pour la classe 130 °C,
105 °C pour la classe 155 °C et
125 °C pour la classe 180 °C.
Les normes CSA supposent que l'échauffement à pleine charge sera le même pour toute température ambiante comprise entre 10 °C et 40 °C.
Ceci permet au manufacturiers de vérifier l'échauffement de leurs moteurs dans des températures ambiantes plus confortables que 40 °C.
Il est intéressant de remarquer que pour les moteurs à courant alternatif ayant une puissance inférieure à 750 W, on a établi une température ambiante normalisée de 30 °C (courbe 4).
La plupart de ces moteurs sont installés dans des résidences où la température n'atteint pas les valeurs élevées que l'on rencontre dans certaines industries. Le choix de 30 °C au lieu de 40 °C implique des échauffements de 10 °C plus élevés, soit 70 °C pour la classe 105 °C.
Cela permet d'augmenter la puissance que l'on peut tirer de ces moteurs.
Les normes d'échauffement dépendent non seulement de la classe d'isolant utilisée mais également du genre d'appareil (moteur, transformateur, relais, etc.), de sa construction (abrité, blindé, etc) et de son application (commerciale, industrielle, navale, etc).
Il est donc important de consulter les normes avant de faire un essai d'échauffement sur une machine.
Mesure de l'échauffement
On peut déterminer l'échauffement d'une machine par la méthode de l'augmentation de résistance. Cette méthode consiste à mesurer la résistance d'un enroulement à froid à une température connue, et de nouveau lorsque l'enroulement est chaud.
Si le bobinage est en cuivre, la température à chaud est donnée par la formule:
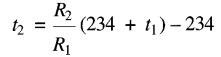 (29-3)
(29-3)
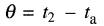 (29-4)
(29-4)
où
t2 =
température de l'enroulement à chaud [°C]
R2 = résistance de l'enroulement à chaud [Ω]
R1 = résistance de l'enroulement à froid [Ω]
t1 = température de l'enroulement à froid [°C]
234 = constante égale à 1/a = 1/0,00427
θ = échauffement de l'enroulement [°C]
ta = température ambiante lorsque l'enroulement est chaud [°C]
Exemple 29-3
L'inducteur shunt d'un moteur de 500 kW, 300 V, arrêté depuis quelques jours. possède une résistance de 44,6Ω.
La température ambiante est alors de 23 °C.
Lorsque la machine est en marche, à une température ambiante (le 28 °C, la résistance (le l' inducteur est de 59,5Ω.
Calculer:
a) la température de l'enroulement
b) l'échauffement (le l'inducteur shunt
Solution
a) En appliquant la formule (29-3) on trouve :
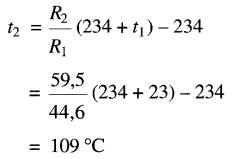
b) L'échauffement est donc:
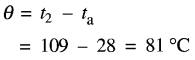
On peut aussi mesurer l'échauffement au moyen d'un thermomètre. Cependant, la température varie beaucoup à différents points de la même machine; si l'on emploie un thermomètre pour déterminer l'échauffement, il est important de le placer sur la partie accessible la plus chaude.
Suivant les calculs ou les préférences du constructeur, le point le plus chaud peut se trouver dans l'induit ou dans l'inducteur.
Étant donné que la température est plus élevée à l'intérieur même des enroulements, un thermomètre ne peut jamais atteindre le point le plus chaud. Cette méthode de mesure de l'échauffement n'a donc qu'une valeur comparative.
Pour la plupart des machines possédant un système d'isolation classe 105 °C, l'échauffement admissible mesuré par la méthode du thermomètre est de 40 °C.
Exemple 29-4
La plaque signalétique d'un moteur indique un échauffement (« temperature risc») de 40 °C.
Au moyen d'un thermomètre, on trouve que la température de la partie la plus chaude de la machine est de 67 °C. la machine fonctionnant à pleine charge. La température de l'air environnant est alors de 30 °C.
Déterminer si la machine surchauffe.
Solution
L'échauffement est de 67° - 30° = 37 °C, alors que l'échauffement permis est de 40 °C. La machine n'est donc pas trop chaude.
Certaines machines sont isolées au mica, au verre ou avec d'autres isolants minéraux qui peuvent supporter des températures beaucoup plus élevées que les isolants organiques des machines ordinaires. On admet alors une limite d'échauffement, mesuré par thermomètre, supérieure aux valeurs conventionnelles de 40° ou 55 °C.
FACTEURS AFFECTANT LA GROSSEUR ET LE RENDEMENT DES MACHINES ÉLECTRIQUES
Une machine électrique est caractérisée par les trois grandeurs nominales suivantes : tension, puissance et vitesse.
Dans les quatre sections qui suivent nous démontrons comment ces trois grandeurs affectent la taille et le rendement des machines.
Les explications sont basées sur des exemples numériques concrets utilisant une génératrice à c.c. Cependant, les conclusions obtenues pour cette machine à c.c. (moteur ou génératrice) s'appliquent aussi bien à une machine à courant alternatif (c.a.).
Impact de la tension nominale sur les dimensions
Considérons une génératrice à c.c. de 100 kW, 125 V, 1800 r/min dont le courant de pleine charge est 800 A. Supposons que l'on désire construire une génératrice semblable mais fonctionnant à 250 V. Les dimensions vont-elles changer ?
Pour répondre à cette question nous utilisons le raisonnement suivant.
Étant donné que la nouvelle machine aura la même puissance de 100 kW, mais une tension deux fois plus grande, il s'ensuit que le courant sera deux fois plus petit. Par conséquent, pour conserver la même densité de courant (A/m²) dans les conducteurs de l'induit, on peut réduire leur section de moitié.
Toutefois, afin de générer une tension de 250 V au lieu de 125 V avec le même flux provenant des pôles, il faudra deux fois plus de conducteurs sur l'induit. Il s'ensuit que la quantité de cuivre dans les encoches demeure la même. En d'autres mots, à moins que la tension devienne très élevée, ce qui exigerait une augmentation de l'isolation,
Les dimensions d'une machine tournante ne changent pas lorsque l'on change sa tension nominale.
De plus, comme la densité de courant dans les conducteurs reste la même, les pertes Joule et par conséquent le rendement demeurent également inchangés. Nous allons voir qu'il en est tout autrement lorsqu'on change la puissance nominale.
Variation des dimensions et du rendement en fonction de la puissance nominale
Considérons maintenant une génératrice à c.c. ayant les caractéristiques fournies dans la première colonne du tableau 29-2, soit la Machine 1.
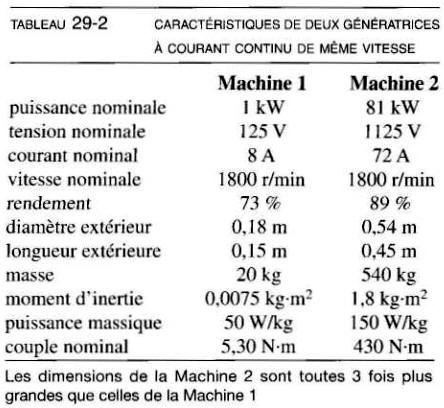
Utilisons la puissance nominale Pη et le rendement η de la Machine 1 pour calculer la puissance mécanique Pm requise pour l'entraîner, de même que ses pertes.
Or, on a:
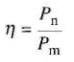 éq. 29-2
éq. 29-2
0,73 = 1 kW / Pm
donc Pm = 1 kW / 0,73 = 1,37 kW
d'où les pertes = Pm - Pη = 1,37 - 1,0 = 0,37 kW
Les pertes comprennent les pertes Joule dans les enroulements, les pertes par hystérésis et courants de Foucault dans le fer, ainsi que les pertes par friction et ventilation.
Considérons maintenant une deuxième machine (Machine 2) plus grosse que la Machine 1.
Pour cette nouvelle machine, nous augmentons toutes les dimensions (longueur, diamètre, profondeur des encoches, entrefer, etc.,) par un même facteur, tout en conservant les mêmes matériaux.
Donc, si on a utilisé un type particulier de tôles pour l'induit de la Machine 1, on utilisera les mêmes tôles (même épaisseur) pour la Machine 2. On conserve également le même type d'isolation.
À l'exception de l'épaisseur des tôles, tout est donc grossi par un même facteur, incluant les roulements à billes, les boulons et les écrous. Ce facteur d2ldi est le rapport entre les dimensions d1 de la Machine 2 et les dimensions correspondantes dl de la Machine 1.
Pour notre Machine 2, nous imposons les deux contraintes de design suivantes: la densité de courant dans les conducteurs (A/m²) et la densité de flux dans l'acier et dans l'entrefer (teslas) restent les mêmes que pour la Machine 1.
Il s'ensuit que les pertes massiques respectives (W/kg) dans le cuivre et dans l'acier sont inchangées. Les pertes respectives augmenteront donc en proportion de la masse, donc du volume du cuivre et de l'acier.
Supposons que les pertes par friction et ventilation augmentent aussi dans les mêmes proportions. Nous supposons en outre que la Machine 2 utilise le même nombre d'encoches et de conducteurs, et que sa vitesse de rotation (1800 r/min) est la même que pour la Machine 1.
Une fois ces hypothèses établies, il est possible de prévoir les caractéristiques de la Machine 2. Supposons, par exemple, que toutes les dimensions dl de la Machine 1 soient augmentées par un facteur 3.
Ainsi, le diamètre augmente de 0,18 m à 0,54 m et la longueur augmente de 0,15 m à 0,45 m, comme l'indique le tableau 29-2.
Quels seront la puissance nominale et le rendement de la Machine 2?
Premièrement, le volume augmentera par un facteur (d2ldi)³ = 3³ = 27.
Par conséquent, les masses respectives augmentent aussi par un facteur 27.
Comme les pertes massiques restent constantes, les pertes respectives augmentent également par un facteur 27. Notre Machine 2 a donc une masse de 20 kg x 27 = 540 kg, et ses pertes sont de 0,37 kW x 27 = 10 kW.
Deuxièmement, les encoches sont 3 fois plus profondes et 3 fois plus larges.
Comme le nombre de conducteurs par encoche n'a pas changé, les conducteurs ont une section 9 fois plus grande. Comme on veut conserver la même densité de courant, ces conducteurs peuvent donc porter un courant 9 fois plus grand. Le courant nominal de notre Machine 2 est donc 8 A x 9 = 72 A.
Troisièmement, en ce qui concerne la tension induite, celle-ci est gouvernée par l'équation (17-2) E = Blv.
Dans cette équation, B représente la densité de flux dans l'entrefer qui, rappelons-le, n'a pas changé, l est la longueur des conducteurs qui a augmenté par un facteur 3, et v est vitesse à laquelle les conducteurs coupent les lignes de flux.
Comme la vitesse de rotation (1800 /min) ne change pas et que le diamètre fut augmenté par un facteur 3, la vitesse v augmente également par un facteur 3.
En conclusion, la tension nominale de notre Machine 2 augmente par un facteur 9, soit 125V x 9= 1125V.
Donc en triplant les dimensions dl, nous avons augmenté le courant nominal de même que la tension nominale par un facteur 9, ce qui correspond à une augmentation de la puissance nominale de 9 x 9 = 81.
La puissance nominale Pn2 de notre Machine 2 est donc de 1 kW x 81 = 81 kW. En multipliant les dimensions dl par 3, la puissance nominale est donc multipliée par 34 = 81.
En généralisant ce raisonnement, on arrive à une première conclusion importante:
À vitesse constante, la puissance nominale varie avec l'exposant 4 des dimensions, soit
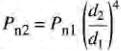 (29-5)
(29-5)
où
Pn1 =
puissance nominale de la Machine 1 [W]
Pn2 = puissance nominale de la Machine 2 ayant la même vitesse que la Machine 1 [W]
d2/d1 = rapport entre les dimensions d2 de la Machine 2 et les dimensions d1 de la Machine 1
Voyons maintenant l'impact de cette augmentation des dimensions sur le rendement.
La puissance mécanique Pm2 requise pour faire tourner la Machine 2 est:
Pm2 = Pn2 + pertes = 81 kW + 10 kW = 91 kW
Le rendement est donc:
η =Pn2 / Pm2 = 81 kW / 91 kW = 0,89 = 89 %
En augmentant les dimensions de notre Machine 1 par un facteur 3, on obtient donc une augmentation considérable du rendement, soit de 73 % à 89 %.
Ceci est dû au fait que la puissance de sortie augmente par un facteur (d2/d1) 4 = 34 = 81 alors que les pertes n'augmentent que par un facteur (d2/d1)³ = 3³ = 27.
Cela démontre clairement que pour une vitesse donnée le rendement d'une machine augmente avec sa grosseur, donc avec sa puissance. La puissance massique de la Machine 1 est de 1 kW / 20 kg = 1000 W / 20 kg = 50 W/kg.
En ce qui concerne la Machine 2, on a une puissance nominale de 81 kW pour une masse de 540 kg, soit une puissance massique de 81 kW/540 kg = 150 W/ kg.
Cela représente un gain par un facteur 3 sur la puissance développée par unité de masse. La grosse machine est donc relativement plus légère et moins coûteuse que la petite.
On peut apprécier le gain obtenu en disant que si l'on avait décidé de générer une puissance de 81 kW avec des Machines 1 (1 kW), il aurait fallu 81 de ces machines, pour une masse totale de 81 x 20 kg = 1620 kg, alors que l'on arrive au même résultat avec une Machine 2 de 540 kg.
De plus, à cause du rendement plus élevé de la Machine 2 (89 % au lieu de 73 %), l'économie réalisée lors de l'achat est accompagnée d'une économie récurrente sur l'énergie consommée par la turbine ou le moteur entraînant la génératrice.
Regardons maintenant comment évolue le moment d'inertie de l'induit.
Rappelons que le moment d'inertie est proportionnel à la masse de l'induit et au carré de son rayon (voir tableau 1-5).
Donc, lorsque les dimensions sont triplées, le moment d'inertie J = mr² est multiplié par un facteur
(d21d,)3 (d2/d,)2 =33 x 32 = 35 = 243.
Le moment d'inertie de la Machine 2 est donc J= 0,0075 kg. m² x 243 = 1,8 kg.m².
Les caractéristiques de la Machine 2 sont affichées dans la colonne 2 du tableau 29-2, ce qui permet de comparer les caractéristiques des deux machines.
Si l'on continue d'augmenter les dimensions on peut montrer, en suivant le même raisonnement, que l'on pourra atteindre des rendements dépassant 95 %.
La Fig. 29-12 montre la variation du rendement en fonction de la puissance pour la gamme de puissance comprise entre 1 kW et 10 MW.
Figure 29-12 Variation du rendement avec la puissance nominale
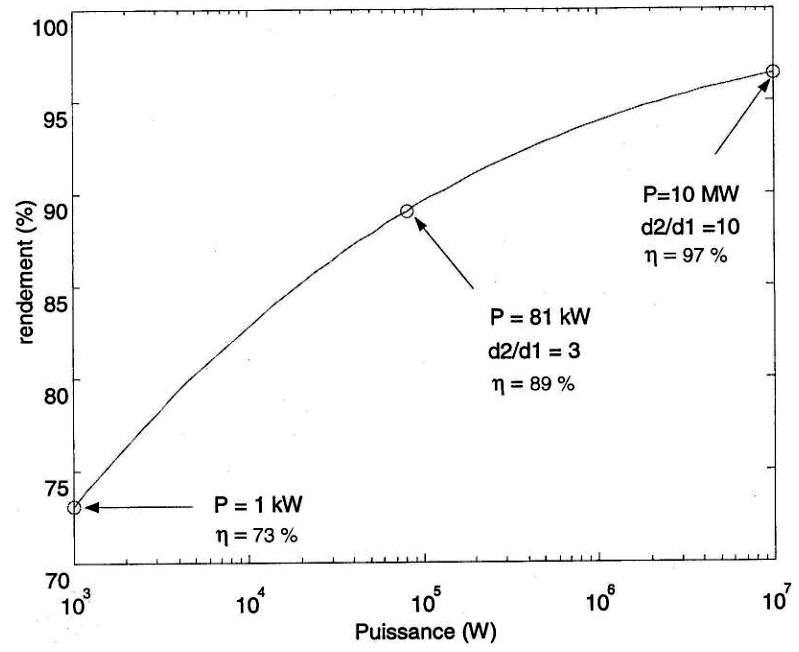
La figure montre que, si l'on augmente les dimensions de notre machine de 1 kW (rendement 73 %) par un facteur d2ld1 = 10, la puissance augmente à 10 000 kW, ou 10 MW. Le rendement grimpe alors à 97 %. Tout semble donc favoriser les grosses machines.
Il existe cependant un problème lorsque l'on augmente la puissance d'une machine. Dans notre exemple, lorsque les dimensions ont été triplées, les pertes ont augmenté par un facteur (d2ld1)³ = 27 alors que la surface extérieure de la machine n'a augmenté que par un facteur (d2ld1)² = 3²= 9.
La puissance dissipée par mètre carré a donc augmenté par un facteur 3.
Par conséquent, à moins d'améliorer l'évacuation de la chaleur, la Machine 2 de 81 kW sera beaucoup plus chaude que la Machine 1. Pour prévenir une dégradation des matériaux isolants, on doit limiter la température.
Le refroidissement devient donc une préoccupation très importante pour les concepteurs de grosses machines.
Concluons en disant que la taille, la puissance, le rendement et les problèmes de refroidissement évoluent de la même manière pour les machines à c.a. qu'avec les machines à c.c.
Ces conclusions s'appliquent aux machines rotatives fonctionnant en moteur ou en génératrice, et même aux appareils stationnaires comme les transformateurs.
Variation des dimensions avec la vitesse nominale
Dans la section précédente nous avons vu que, pour une vitesse nominale donnée, la puissance nominale et le rendement d'une machine varient très rapidement avec les dimensions de la machine.
Mais pour une puissance donnée, quel est l'impact de la vitesse nominale sur les dimensions?
Pour répondre à cette question revenons à notre Machine 1 ayant une puissance nominale de 1 kW, une tension nominale de 125 V et une vitesse nominale de 1800 r/min.
Supposons que l'on désire construire une machine ayant la même puissance, mais qui fonctionne à une vitesse nominale deux fois plus faible, soit à 900 r/min.
Nous conserverons les mêmes contraintes de conception (même densité de courant dans les conducteurs et même densité de flux dans l'entrefer). Désignons cette machine par Machine 3.
Si l'on ne change pas les dimensions de la Machine 1, les encoches de la Machine 3 logeront les mêmes conducteurs. Par conséquent, l'induit peut débiter le même courant I.
Comme le nombre total de conducteurs sur l'induit n'a pas changé, la tension nominale E est donc réduite par 2, soit de 125V à 62.5V.
La puissance nominale, qui est proportionnelle à EI, est également réduite par 2, si bien qu'on ne dispose plus que d'une puissance nominale Pn3 de 0,5 kW.
Afin d'augmenter la puissance nominale de la Machine 3 à 1 kW, on n'a pas d'autre choix que d'augmenter les dimensions de la génératrice.
Or, on a vu que lorsque la vitesse est constante, la puissance varie comme (d2ld1)4, soit:
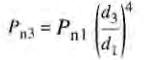 éq.
29-5
éq.
29-5
D'où l'on tire:
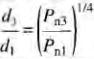 (29-6)
(29-6)
On en déduit le rapport requis pour augmenter la puissance de la Machine 3 de 0,5 kW à 1 kW :
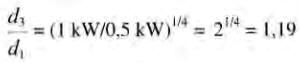
En d'autres termes, pour réduire la vitesse par un facteur 2 tout en gardant la même puissance de 1 kW, on doit augmenter toutes les dimensions de 19 %.
La Fig. 29-13 compare les dimensions de deux machines de 100 kW, 125V ayant respectivement une vitesse de 1800 r/min et 900 r/min.
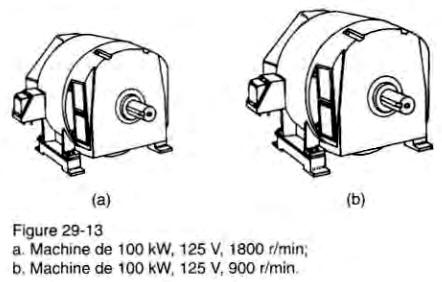
En généralisant ce raisonnement, on arrive à la conclusion qu'à puissance constante, le rapport d2/d1 de deux machines fonctionnant à des vitesses différentes est donné par l'expression:
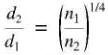 (29-7)
(29-7)
où
n1 =
vitesse nominale de la Machine 1 [W]
n2 = vitesse nominale de la Machine 2 ayant la même puissance que la Machine 1 [W]
d2/d1 = rapport entre les dimensions de la Machine 2 et les dimensions de la Machine 1, les deux machines ayant la même puissance.
On constate donc qu'une machine est d'autant plus grosse que sa vitesse nominale est plus basse. Le coût d'une machine à basse vitesse est donc plus élevé que celui d'une machine à haute vitesse. Lorsque la vitesse désirée est très basse, il est souvent plus économique d'utiliser un moteur à haute vitesse connecté à une boîte de vitesse.
Couple nominal et dimensions d'une machine
Il est utile de combiner les résultats énoncés dans les équations (29-6) et (29-7) en une seule expression. En effet, lorsque, à la fois, la puissance nominale et la vitesse de rotation nominale varient, on obtient l'expression « universelle » suivante :
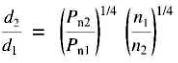 (29-8)
(29-8)
Rappelons la relation entre la puissance P, la vitesse de rotation n et le couple T d'une machine rotative, soit:
P = nT / 9,55 éq. 1-5b
Pour une puissance nominale Pn et une vitesse nominale nn, le couple nominal Tn est donné par l'expression:
Tn = 9,55 Pn / nn
De l'équation 29-9 on peut déduire la relation suivante entre les valeurs nominales respectives de deux machines:
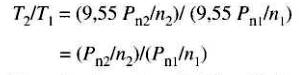 (29-10)
(29-10)
En combinant les équations 29-10 et 29-8, on obtient la relation très intéressante :
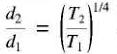 (29-11)
(29-11)
où
T1 =
couple nominale de la Machine 1 [W]
T2 = couple nominale de la Machine 2 [W]
d2 / d1 = rapport entre les dimensions de la Machine 2 et les dimensions de la Machine 1
Cette équation montre que la grosseur d'une machine rotative dépend fondamentalement de son couple nominal, peu importe sa vitesse. Le couple nominal est défini selon l'équation (29-9).
Ainsi, le couple nominal de notre Machine 1 est donné par:
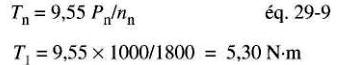
Exemple 29-5
Un moteur d'induction triphasé de 7.5 hp, 3600 r/min, 460 V, de type abrité, possède un poids de 78 kg et un rendement de 57,5 %.
Déterminer:
a) le poids
et b) le rendement d'un moteur semblable de 600 V ayant une puissance de 200 hp et une vitesse nominale de 1800 r/min.
Solution
a) Trouvons d'abord le rapport d2ld1 en utilisant l'équation 29-8.
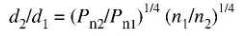 éq. 29-8
éq. 29-8
On obtient
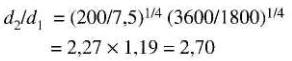
Comme le poids varie selon le rapport (d2ld1)³ on trouve que la masse du moteur de 200 hp est de
2,70³ x 78 = 19,7 x 78 = 1537 kg
b) La puissance mécanique du moteur est de 7,5 hp x 746 = 5595 W
Comme le rendement est de 87,5 %, la puissance électrique fournie au moteur est de 5595 W/0,875 = 6394 W
Les pertes dans le moteur de 7,5 hp: pertes = 6394 - 5595 = 799 W
Comme les pertes varient selon le rapport (d2ld1)³, il s'ensuit que les pertes dans le moteur de 200 hp seront de 799 x 2,703 = 15 727 W.
La puissance mécanique du moteur de 200 hp est de 200 x 746 = 149 200 W.
La puissance électrique absorbée par le moteur est de 149 200 + 15 727 = 164 927 W.
Le rendement du moteur de 200 hp est donc de 149 200/164 927 = 0,905 = 90,5 %
Nous tenons à signaler que les valeurs du poids et du rendement que nous venons de calculer sont très approximatives.
En effet, les valeurs ainsi calculées sont basées sur une densité de courant et une densité de flux qui sont maintenues constantes.
Or, il est fort possible que ces valeurs aient été modifiées par le concepteur afin (entre autres choses) de garder l'échauffement du moteur à un niveau acceptable. Cependant, cette méthode de prédire le poids et le rendement des machines donne un ordre de grandeur des valeurs réelles.
Notons aussi que l'extrapolation que nous avons utilisée peut seulement se faire pour les machines d'une même famille.
Par exemple, on ne peut pas utiliser les caractéristiques d'un moteur à c.a. abrité pour estimer les caractéristiques d'un moteur à c.a. blindé.
Exemple 29-6
Un moteur monophasé de 113 fil), 1725 r/min, 230 V, 60 Hz. isolation classe B, pèse 5,9 kg et possède un rendement de 68 %.
Estimer
a) le poids
et b) le rendement approximatif d'un moteur semblable de 1725 r/train, 115 V, 60 Hz dont la puissance est de 1 / 100 hp.
On sait que la carcasse du moteur à une longueur de 150 mm et un diamètre de 146 mm.
c) Estimer le diamètre du moteur de 1/100 hp.
Solution
a) Déterminons d'abord le rapport des dimensions d2ld1.
On sait que la tension d'opération n'affectera pas la grosseur du moteur. Comme la vitesse demeure essentiellement la même, il s'ensuit que le couple du moteur de 1/100 hp est 33,3 fois plus petit que celui de 1/3 hp.
On peut donc écrire:
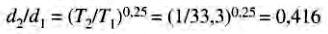
La masse du moteur varie selon
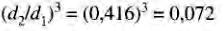
Le moteur de 1/100 hp aura un poids approximatif de 0,072 x 5,9 kg = 0,42 kg
b) Puissance fournie au moteur de 1/3 hp P = 1/3 x 746/0,68 = 365,7 W
Pertes dans le moteur = 365,7 - (1/3) x 746 = 117 W
Pertes dans le moteur de 1/100 hp = 117 x (d2ld1)³ = 117 x (0,416)³ = 8,42 W
Puissance équivalente de 1/100 hp = 746 x 1/100 = 7,46 W
Puissance à fournir au moteur = 7,46 + 8,42 = 15,9 W
Rendement du moteur de 1/100 hp = 7,46/15,9 = 0,469 = 46,9 %
c) Le diamètre du moteur de 1/100 hp sera environ 146 mm x d2ld1 = 146 x 0,416 = 61 mm.
Résumé
La transformation d'énergie dans les machines comme les génératrices, les moteurs, les transformateurs, ne peut s'effectuer sans pertes.
Ces pertes provoquent un échauffement de la machine et une diminution du rendement. Les pertes et donc le rendement d'une machine varient avec la charge.
On distingue les pertes mécaniques par frottement et les pertes électriques dans les conducteurs et dans le fer. Les pertes dans les conducteurs sont dues à l'effet Joule.
Les pertes massiques (W/kg) dépendent de la densité de courant utilisée, de la résistivité et de la masse volumique du conducteur. Les pertes dans le fer sont dues au phénomène d'hystérésis et aux courants de Foucault.
Les pertes massiques dans le fer dépendent de la densité de flux et de la fréquence, ou de la vitesse de rotation.
L'utilisation de tôles minces permet de réduire les pertes par courants de Foucault. Des courbes fournies par les manufacturiers permettent d'évaluer les pertes dans le fer pour différents types d'acier.
L'échauffement permis pour les machines est établi par les organismes de normalisation. Les normes de température établissent différentes classes de température selon le type d'isolant.
Chaque classe correspond à une température maximale permise, allant de 105 °C à 180 °C. Pour mesurer l'échauffement on peut déterminer directement la température du point chaud à l'aide d'un thermocouple ou déduire la température moyenne des enroulements en mesurant leur augmentation de résistance.
Finalement, nous avons étudié l'impact de la tension nominale, de la puissance nominale et de la vitesse nominale d'une machine, sur sa grosseur et son rendement.
Retenons que :
(1) la tension nominale d'une machine n'affecte pas ses dimensions ni son rendement,
(2) à vitesse constante, le rendement d'une machine augmente rapidement avec sa puissance nominale
et (3) à puissance constante, une machine est d'autant plus grosse que sa vitesse de rotation est plus basse.
PROBLÈMES
Niveau pratique
29-1 Quelles pertes rencontre-t-on dans un moteur à c.c.?
29-2 À quoi attribue-t-on les pertes dans le fer? Comment peut-on les réduire?
29-3 Expliquer pourquoi la température d'une machine augmente avec la charge.
29-4 Qu'est-ce qui détermine la puissance nominale d'une machine?
29-5 La puissance nominale d'un moteur doit être réduite si l'on bouche les ouvertures d'aération. Expliquer.
29-6 Peut-on surcharger un moteur utilisé dans un endroit très froid? Pourquoi?
Niveau intermédiaire
29-7 Un moteur à c.c. développe une puissance mécanique de 120 kW. Sachant que ses pertes sont de 12 kW et qu'il est alimenté à 240 V, calculer la puissance qu'il absorbe et le courant qu'il tire.
29-8 Une génératrice débite un courant de 120A sous une tension de 115 V et son rendement est de 81 %. Quelle puissance mécanique absorbe-t-elle?
29-9 Calculer le courant de pleine charge d'un moteur à c.c. qui développe 250 kW à 230 V, avec un rendement de 92 %.
29-10 Une machine expérimentale, isolée selon la classe 130 °C et fonctionnant à pleine charge, atteint une température de 124 °C, mesurée par la méthode de l'augmentation de résistance. La température de l'air environnant est de 32 °C.
a) Quelle est l'échauffement de la machine, en °C?
b) Quel est l'échauffement permis selon les normes? c) La machine aurait-elle une durée de vie normale si elle marchait toujours à une température ambiante de 32 °C?
29-11 Le rendement d'une machine est toujours faible lorsqu'on la fait fonctionner à seulement 10 % de sa puissance nominale. Expliquer.
29-12 Calculer le rendement du moteur du tableau 29-1 lorsqu'il débite une puissance de 30 kW.
29-13 Un moteur électrique actionne une grue qui extrait 1,5 tonnes métriques de minerai d'une tranchée de 20 m de profondeur en 30 secondes. En supposant que le rendement de la grue est de 94 %, calculer la puissance fournie par le moteur (en hp et en kW).
29-14 On mesure la température d'un moteur à courant alternatif de 1200 kW possédant une isolation classe 155 °C, à l'aide de thermocouples logés à l'intérieur des enroulements.
Quelle doit être la température maximale indiquée par ces détecteurs lorsque la température ambiante est de 40 °C? 30 °C? 14 °C? (Appliquer les normes décrites plus haut)
29-15 Un moteur à courant alternatif de 60 kW possède un enroulement dont la résistance à 23 °C est de 12Ω. Lorsqu'il fournit sa puissance nominale à une température ambiante de 31 °C, on constate que la résistance de l'enroulement monte à 17,4Ω.
a) Calculer la température de l'enroulement.
b) Quelle est l'échauffement du moteur?
c) Sachant que l'enroulement possède une isolation classe 155 °C. le fabricant aurait-il pu indiquer use: puissance nominale plus grande sur la plaque signalétique du moteur?
29-16 Le moteur du problème 29-15 possède une isolation classe 155 °C et fonctionne à une température ambiante de 12 °C. On lui fait débiter une puissance de 75 kW, soit une surcharge de 15 kW.
Sans que la vie normale du moteur soit raccourcie, quel est alors l'échauffement (mesuré par l'augmentation de résistance) que l'on peut tolérer pour les enroulements?
29-17 Un fil rond n° 10 en cuivre ayant une longueur de 210 m porte un courant de 12 A. La température du conducteur étant de 105 °C, calculer :
a) la densité du courant, en A/mm2
b) les pertes massiques, en W/kg
Niveau avancé
29-18 Un conducteur en aluminium fonctionne à une température de 120 °C. Sachant que la densité de courant est de 2 A/mm2, calculer les pertes massiques en W/kg.
29-19
a) Quelle est la fréquence engendrée dans les tôles (type M-36, jauge 24) de l'induit de la Fig. 28-4a, lorsqu'il tourne à une vitesse de 1200 r/min, sachant que l'inducteur possède 6 pôles. Chaque dent a une largeur de 10 mm, une profondeur de 35 mm et une longueur de 235 mm.
b) Calculer les pertes dans les dents sachant que l'induction maximale dans les 81 dents est de 1,4 T.
29-20 L'échauffement d'un moteur est à peu près proportionnel à ses pertes. D'autre part, son rendement est habituellement assez constant pour toute puissance comprise entre 50 % et 150 % de sa puissance nominale (voir, par exemple, la Fig. 29-9). À pleine charge, un moteur de 20 kW a un échauffement de 80 'C.
Calculer la puissance approximative qu'il pourra débiter si l'on permet un échauffement de 105 °C?
29-21 Un moteur à courant alternatif de 250 W possède une isolation classe 105 °C. a) Selon les normes de l'ACNOR, quel est l'échauffement permis, mesuré par l'augmentation de résistance?
b) Si l'on rebobine le moteur avec une isolation classe 130 °C, quelle sera le nouvel échauffement permis?
Compte tenu des remarques faites au problème 29-20, quelle sera alors la nouvelle puissance approximative du moteur?
29-22 Un moteur à courant alternatif de 10 kW possède une isolation classe 130 °C. Selon les normes de l'ACNOR (Fig. 29-10), ce moteur aura une durée de vie «normale» si la température de ses enroulements (mesurée par augmentation de résistance) ne dépasse pas 120 °C
Si l'on suppose que cette durée de vie normale est de 20 000 h, de combien d'heures la durée de vie sera-t-elle raccourcie si le moteur fonctionne pendant 3 heures à une température de 200 °C?
29-23 L'induit d'un moteur de 300 kW est composé de tôles de jauge n° 24, type M-36.
a) Sachant que la densité de flux est de 1,2 T, de quel pourcentage les pertes diminueraient-elles si le fabricant utilisait de la tôle de jauge n° 29, type M-14?
b) Quels sont les avantages de cette diminution des pertes?
c) Quels sont les inconvénients à utiliser ce type de tôle? 29-24 La plaque signalétique du moteur illustré à la Fig. 29-14 affiche les informations suivantes :
Puissance 350 hp
vitesse nominale 1785 r/min
tension triphasée 575 V
courant par phase 312 A
fréquence 60 Hz
rendement 95,8%
masse 3130 lb
moment d'inertie 74 lb.ft2
couple nominal 1030 lbf.ft
Type de moteur: triphasé à induction, TEFC (« totally enclosed, fan cooled »)
Comme ce moteur est destiné au marché américain, les unités sont exprimées en « American customary units ».
En utilisant ces informations, déterminer les valeurs approximatives
a) du poids
b) du rendement
et c) du moment d'inertie pour un moteur triphasé semblable de 25 hp, 460 V, 1150 r/min.
Réponses
7) 132 kW, 550A; 8) 17,0 kW; 9)
1181 A; 10a) 92°C;
10b) 80°C; 10c) non; 12) 82,9%; 13) 10,4 kW; 14 hp;
14)
155°C; 145°C; 129°C; 15a) 138,7 °C; 15b) 107,6 °C; 15c) non;
16) 133°C; 17a)
2,28 A/mm²; 17b) 13,5 W/kg; 18)58,7 W/kg;
19a) 60 Hz; 19b) 421 W; 20) - 26
kW; 21 a) 70°C; 21 b) 90°C;
21c) - 320 W; 22) 765 h; 23a) 68%