Puissance et énergie électrique

Électrotechnique

Circuit électrique Un circuit électrique est un ensemble comprenant des sources, des conducteurs et des charges.

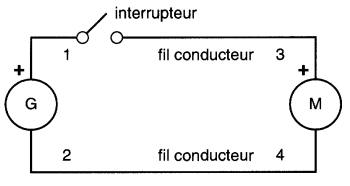
Le schéma de la Fig. 4-1 représente un circuit comprenant un moteur M et un générateur G qui l'alimente par l'intermédiaire de deux fils conducteurs. Le circuit comprend aussi un interrupteur permettant de commander la circulation du courant.

Figure 4-1 Éléments d'un circuit électrique

Si l'interrupteur est ouvert, le courant ne passe pas car l'air constitue un bon isolant. Pour qu'il circule, il faut qu'il y ait une suite ininterrompue de conducteurs reliant les deux bornes du générateur.

Dans la Fig. 4-1, ces conducteurs sont constitués de deux fils conducteurs et des conducteurs situés à l'intérieur du moteur M, entre les bornes 3 et 4. 

Puissance électrique

Nous avons déjà vu que si un courant parcourt une résistance (comme l'élément d'une chaufferette), le frottement des électrons contre les atomes donne naissance à un dégagement de chaleur.

Puisque la chaleur est une forme d'énergie et que l'élément seul ne peut pas la produire, il s'ensuit que cette énergie doit provenir du générateur (Fig. 4-2).

Figure 4-2 Chaleur dégagée par une résistance

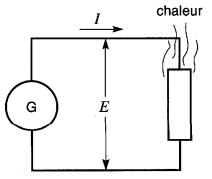
On peut prouver expérimentalement que la puissance dégagée sous forme de chaleur est directement proportionnelle à la tension E aux bornes de la résistance et au courant I qui la traverse.

La puissance électrique fournie par le générateur est, par suite, proportionnelle à ces deux mêmes grandeurs E et I. Il existe donc une relation étroite entre la puissance, la tension et le courant électrique.

Expression de la puissance

La puissance (P) dépensée par un courant électrique entre deux points d'un circuit s'obtient toujours par le produit de la tension (E) entre ces deux points et de l'intensité (I) du courant:

P = EI  (4-1)

où

P = puissance, en watts [W]

E = tension, en volts [V]

I = courant, en ampères [A]

Tout comme pour l'expression de la loi d'Ohm, on peut facilement déterminer un des facteurs de l'expression de la puissance lorsqu'on connaît les deux autres .

Selon que l'on cherche la puissance P, l'intensité I ou la tension E, on utilise respectivement les formules:

P = EI ou I = P/E ou E = P/I   (4-2)

En appliquant ces formules, les trois exemples numériques suivants peuvent être facilement résolus.

Exemple 4-1

Évaluer la puissance fournie à un moteur qui tire 15 A sous 120 V.

P= EI = 120Vx15A = 1800W

Exemple 4-2

Une génératrice produit une puissance de 3 kW sous une tension de 240 V.

Quel est le courant débité ?

on a I = P / E

d'où le courant  I = 3000 W / 240 V = 12,5 A

Exemple 4-3

Un courant de 3 A circule entre deux points d'un  circuit et transporte une puissance de 18 W.

Déterminer la tension entre ces points.

on a E= P / I

d'où la tension E = 18W / 3A = 6 V

Puissance d'une génératrice

La Fig. 4-3 montre une génératrice G entraînée par une turbine.

Figure 4-3 L'énergie électrique est transportée de la source à la charge par des fils conducteurs

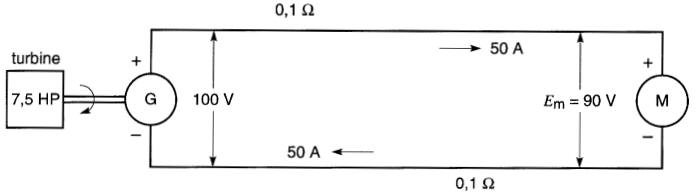
La génératrice alimente un moteur M par l'entremise d'une ligne électrique composée de deux fils conducteurs. Imaginons que le circuit électrique soit fermé, et que la différence de potentiel aux bornes de la génératrice soit de 100 V.

Pour une tension fixe (ce qui est généralement le cas des réseaux de distribution), le courant qui circule dans ce circuit dépend exclusivement de la résistance des fils conducteurs et des caractéristiques électriques de la charge.

Supposons que le circuit soit parcouru par un courant de 50 ampères. La génératrice devra donc débiter une puissance électrique de:

P = EI = 100 x 50 = 5000 W = 5 kW

Pour fournir cette puissance électrique de 5 kW elle devra elle-même recevoir une certaine puissance mécanique de la turbine.

En supposant que la transformation de l'énergie par la génératrice se fasse sans aucune perte (sans aucun dégagement de chaleur et sans frottement), la valeur de cette énergie mécanique reçue, évaluée en horsepower sera de:

P = 5000 / 746= 6,7 HP, car un HP vaut 746 watts

Par contre, si le rendement de la génératrice n'est que, disons, de 84 %, la puissance de la turbine qui l'entraînera devra être de 6,7 HP / 0,84 = 8 HP.

Puissance dissipée dans les fils conducteurs (effet Joule)

Le mouvement d'ensemble des électrons libres dans un conducteur est lent car leur chemin est obstrué par des atomes qui les font dévier.

Ces chocs, ces frottements entre les électrons libres et les atomes produisent un dégagement de chaleur, ce qui revient à dire qu'une partie plus ou moins grande de l'énergie électrique transportée par le conducteur est transformée en énergie thermique.

Ce phénomène d'échauffement d'un conducteur par le courant d'électrons constitue l'effet Joule: il sera évidemment d'autant plus grand que le nombre d'électrons en mouvement orientés dans un conducteur sera plus considérable.

La chaleur dégagée dans les conducteurs d'une ligne de transport (ou dans les enroulements d'un moteur) augmentera donc avec la charge.

Puisque ces pertes dépendent du courant, il est utile de connaître l'expression de la puissance consommée par effet Joule en fonction du courant.

D'après la loi d'Ohm, la chute de tension E dans un conducteur est égale au produit de sa résistance R par l'intensité du courant I

E = RI  éq. 3-3

Si, dans la formule générale de la puissance consommée dans un circuit, P = EI, on remplace la tension E par la valeur RI, on obtiendra pour l'expression de la puissance électrique transformée en chaleur:

 P = EI = (RI) x I

P=RI²     (4-3)

où

P = puissance dissipée en chaleur [W]

I = courant dans le conducteur [A]

R = résistance du conducteur [Ω]

On voit ainsi que, pour un conducteur donné, la puissance dépensée par effet Joule, est proportionnelle au carré de l'intensité du courant: si le courant double, le dégagement de chaleur quadruple.

Les conducteurs utilisés le plus souvent dans les appareils électriques étant des fils de cuivre, les pertes Joule sont parfois appelées «pertes dans le cuivre».

Si l'intensité triple, l'échauffement sera 9 fois plus grand.

Pertes dans les lignes de transport

Si la résistance de chacun des fils conducteurs de la Fig. 4-3 est égale à 0,1 52, la puissance dépensée en chaleur pour une intensité de 50 ampères sera :

P = RI² = 0,1 x (50 x 50) = 250 W par fil, soit 500 W pour la ligne

Une partie des 5000 watts fournis par la génératrice à l'entrée de la ligne sera transformée inutilement en chaleur le long des fils conducteurs . La puissance électrique transmise à la charge ne sera donc plus que :

P = 5000 - (2 x 250) = 4500 W

Ces pertes inévitables par effet Joule dans les lignes de transport sont analogues aux pertes par frottement dans les machines.

Dans celles-ci, une partie de l'énergie mécanique est transformée inutilement en chaleur.

Il s'ensuit que les lignes de transport d'énergie électrique doivent avoir une résistance aussi faible que possible pour réduire les pertes par effet Joule ; elles utilisent des câbles de grande section, constitués générale- ment de métaux bons conducteurs (cuivre ou aluminium).

Chute de tension dans les lignes de transport

La résistance de chaque fil conducteur de la Fig. 4-3 est de 0,1 S2 et comme le courant est de 50 A, il s'ensuit que la différence de potentiel Ef aux bornes de chaque fil est de:

Ef = RI = 0,1 x 50 = 5V

Cette différence de potentiel est appelée chute de tension dans le fil conducteur. La chute de tension totale dans la ligne (deux conducteurs) est donc de 10 V.

La tension de la source est de 100 V, mais à cause de la chute de tension de 10 V le long de la ligne, la différence de potentiel El, appliquée aux bornes du moteur n'est plus que de 100 V - 10 V = 90 V.

Notons, en passant, que la tension entre les deux fils de ligne diminue progressivement de 100 V à 90 V à mesure que l'on s'éloigne de la source vers la charge.

Par exemple, au centre de la ligne la tension entre les deux fils est de 95 V mais le courant est constant par- tout dans le circuit.

Si l'on utilisait des fils conducteurs de 0,01 0 (résistance 10 fois plus faible qu'auparavant), la chute de tension ne serait plus que de 1 V et la tension aux bornes du moteur monterait alors à 99 V.

Puissance fournie à la charge

La tension aux bornes du moteur de la Fig . 4-3 est de 90 volts, et le moteur est traversé par un courant de 50 A.

La puissance Pm fournie au moteur est donc:

Pm = Eml = 90 V x 50 A = 4500 W

Cette valeur correspond bien à la valeur de la puissance calculée précédemment à la section ci-haut. La plus grande partie de cette puissance électrique absorbée est transformée en puissance mécanique.

Une faible partie sera cependant transformée en chaleur, par effet Joule, dans les enroulements du moteur.

Cas d'un court-circuit

Si les deux fils conducteurs du circuit se touchent en un point situé près du moteur (Fig . 4-4)

Figure 4-4 Un fusible protège un circuit contre les courts-circuits

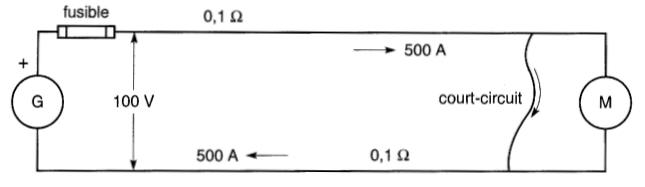
l'intensité du courant sera seulement limitée par la résistance des fils et deviendra:

I= E / R = 100V / 0,2Ω = 500A

C'est là une valeur excessive qui produit un dégagement de chaleur intense. Cette condition, que l'on appelle court-circuit, pour- rait provoquer la destruction de la génératrice et la fusion des fils, avec risque sérieux d'incendie.

Pour limiter les dégâts, on introduit à dessein dans beaucoup de circuits un point faible qui assure automatiquement la rupture du courant lorsque l'intensité devient trop forte. Les dispositifs qui remplissent cette fonction portent le nom de fusibles.

Ce sont habituellement des pièces ou des fils métalliques dont l'alliage et les dimensions sont choisis de façon à ce qu'ils fondent sans danger lorsque la surintensité dépasse une valeur prédéterminée. La fusion de la pièce interrompt le courant.

Charges conçues pour produire de la chaleur

Jusqu'à maintenant nous avons envisagé uniquement les conséquences néfastes de l'effet Joule; il existe toutefois des dispositifs comme les grille-pain, les radiateurs électriques, les fers à repasser, etc ., qui sont spécialement conçus pour convertir la puissance électrique en chaleur.

On les raccorde au réseau domiciliaire dont la tension, malgré des fluctuations occasionnelles, demeure sensiblement constante.

Pour ces appareils, on préfère utiliser une formule qui donne la puissance P en fonction de leur résistance R, et de la tension E appliquée à leurs bornes.

En utilisant les équations P = EI et I = E/R, on déduit que P = E x (E/R)

d'où

P = E² / R  (4-4)

où

P = puissance dissipée en chaleur [W]

E = tension aux bornes de l'élément [V]

R = résistance de l'élément [Ω]

Cette équation démontre que la puissance varie avec le carré de la tension appliquée.

Donc, lorsque la tension double, la puissance quadruple; inversement, lorsque la tension baisse de 10 %, la chaleur dégagée diminue de 19 %. Les appareils de chauffage sont donc très sensibles aux variations de tension.

Remarquons que les appareils de chauffage sont les seuls appareils électriques à posséder un rendement de 100 %; en effet toute l'énergie électrique absorbée se retrouve convertie en chaleur.

Distinction entre «source» et «charge»

Tout élément de circuit traversé par un courant est soit une source, soit une charge. Une source débite une puissance électrique tandis qu'une charge en absorbe.

Afin de mettre en évidence les différences entre les notions de source et de charge, supposons que dans le circuit de la Fig. 4-5 les deux éléments A et B renferment des dispositifs quelconques dont nous ignorons la nature (source ou charge).  

Figure 4-5 Identification d'une source et d'une charge

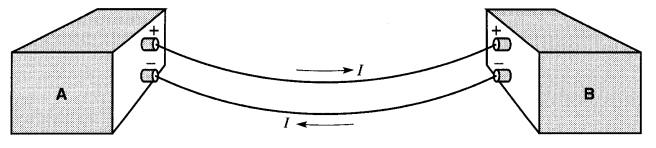
Admettons que des mesures au voltmètre et à l'ampèremètre aient fourni les polarités de tensions et les sens de courants indiqués sur la figure.

Comment identifier alors la source et la charge ?

On y arrive facilement en observant (1) la polarité des bornes de chaque élément; (2) la direction correspondante du courant, et (3) en appliquant la règle suivante:

si le courant sort de la borne (+), l'élément est une source ;

si le courant entre par la borne (+), l'élément est une charge.

Nous constatons d'après cette règle que l'élément A est une source et l'élément B, une charge. Cette distinction importante entre source et charge nous aidera à comprendre les échanges d'énergie dans les circuits électriques .

Énergie électrique

On a vu à la section Notions fondamentales et circuits électriques que la puissance mécanique dépendait du taux d'utilisation de l'énergie mécanique.

Il en est de même pour la puissance et l'énergie électriques. La puissance électrique P représente le taux d'utilisation de l'énergie électrique W, c'est-à-dire l'énergie électrique divisée par le temps.

Inversement, l'énergie est la puissance électrique multipliée par le temps.

On peut donc écrire l'équation (1-4) sous la forme:

W = Pt    (4-5)

où

W = énergie électrique, en joules [J]

P = puissance électrique, en watts [W]

t = temps, en secondes [s]

L'unité SI d'énergie électrique est le joule ; 1 joule est égal à 1 watt-seconde. Si l'on exprime la puissance en kilowatts et le temps en heures, l'énergie électrique est donnée en kilowattheures (kWh).

Le kilowattheure n'est pas une unité SI, mais on l'utilise pour évaluer la consommation d'énergie électrique dans les maisons et les usines (1 kW.h = 3 600 000 J = 3,6 MJ).

Exemple 4-4

Une lampe de 100 W allumée pendant 20 secondes consomme 100 watts x 20 secondes, soit 2000 watt-secondes d'énergie, ce qui équivaut à 2000 joules.

De la même façon, un alternateur de 1,50 kW fournit pendant 20 heures une quantité d'énergie égale à 150 kW x 20 h. soit 3000 kW.h,

Exprimée en joules, cette énergie équivaut à 3000 x 3.6 x 10⁶ = 10,8 x 10⁹j = 10,8 gigajoules = 10,8 GJ.

Emmagasinage de l'énergie

D'énormes quantités d'énergie chimique sont emmagasinées dans les puits de pétrole et les mines de char- bon de la terre. Lors de la combustion de ces matériaux on libère de l'énergie thermique, qui peut à son tour être convertie en énergie électrique.

Nous pouvons aussi emmagasiner de grandes quantité d'énergie mécanique en érigeant des barrages derrière lesquels l'eau accumulée sert à faire tourner les turbines d'une centrale hydro-électrique.

Une autre façon d'emmagasiner une quantité importante d'énergie mécanique est de comprimer de l'air dans un réservoir pour actionner des outils pneumatiques. L'énergie nucléaire renfermée dans les mines d'uranium représente une autre source très concentrée d'énergie.

Malheureusement, il n'existe aucune méthode permettant d'emmagasiner des quantités importantes d'énergie électrique.

Les batteries, par exemple, n'emmagasinent pas de l'énergie électrique, mais plutôt de l'énergie chimique qui est libérée sous forme d'électricité lors de la transformation de leurs éléments chimiques.

Seulement deux dispositifs, la bobine et le condensateur, peuvent conserver l'énergie électrique à son état naturel ; cependant, si on tient compte de leur grosseur et de leur coût, ces dispositifs emmagasinent très peu d'énergie.

En effet, l'énergie maximale qu'on pourrait emmagasiner dans une bobine conventionnelle pesant 2 tonnes (2000 kg) suffirait à peine à faire briller une lampe de 100 watts pendant deux minutes.

Les dimensions d'un condensateur pouvant emmagasiner la même énergie seraient encore plus grandes.

Cette difficulté d'emmagasiner des grosses quantités d'énergie électrique constitue le problème de base des compagnies d'électricité et les oblige à produire l'énergie au même rythme qu'elle est consommée par l'utilisateur.

Si l'énergie consommée diffère légèrement de celle produite, le réseau électrique réagit violemment, provoquant des surtensions ou des excès de courants, lesquels entraînent l'ouverture immédiate des disjoncteurs pour ne pas risquer l'arrêt complet du système.

Si l'on pouvait, un jour, conserver l'énergie électrique aussi simplement que l'on conserve l'énergie chimique dans un litre de pétrole, la production, le transport et l'utilisation de l'électricité en seraient profondément modifiés.

Résumé

Un circuit électrique est un ensemble de sources et de charges interconnectées par des conducteurs. Pour chaque appareil on peut calculer la puissance électrique générée (pour une source) ou absorbée (pour une charge).

Cette puissance P en watts est toujours don- née par le produit de la tension E en volts à ses bornes et du courant I en ampères qui le traverse (P = EI).

Pour savoir si un appareil agit comme une source ou une charge il suffit de noter le sens du courant par rap- port à sa borne positive. Si le courant sort de la borne positive il s'agit d'une source.

S'il entre dans la borne positive, il s'agit d'une charge. À tout instant la somme des puissances générées par les sources est égale à la somme de puissances absorbées par les charges et les conducteurs d'interconnexion.

Des pertes de puissance sont dissipées sous forme de chaleur (effet Joule) dans les conducteurs .

Le courant circulant dans les conducteurs provoque aussi une chute de tension entre la source et la charge. À partir de la loi d'Ohm on peut dériver deux autres expressions pratiques de la puissance :

P = RI² et P = E²/R

La première est utile lorsque le courant est imposé (ex. : calcul des pertes Joule dans un conducteur) .

La seconde est utile lorsque le tension aux bornes d'une charge de chauffage est imposée.

Enfin, l'énergie électrique W en joules(J) consommée par une charge est obtenue en multipliant sa puissance P en watts par le temps d'utilisation t (W = Pt).

Une autre unité d'énergie utilisée par les compagnies d'électricité pour facturer l'énergie à leurs clients est le kilowattheure (kW.h).

PROBLÈMES

4-1 Pourquoi une résistance chauffe-t-elle lorsqu'elle est parcourue par un courant ?

4-2 Dans quelle proportion le dégagement de chaleur dans un conducteur varie-t-il lorsqu'on diminue de moitié l'intensité du courant qui le traverse ?

4-3 Quand y a-t-il un court-circuit ?

4-4 À quoi servent les fusibles ?

4-5 Énumérer les principales applications de l'effet Joule.

4-6 Quel est le courant tiré par une lampe de 60 W sous une tension de 120 V ?

4-7 L'éclairage d'une maison est assuré par 9 lampes de 100 watts. Trouvez le courant total tiré par ces lampes lorsque la tension du réseau de distribution est de 120 volts.

4-8 Quelle est la différence entre l'énergie électrique et la puissance électrique ?

Quelle est l'unité SI d'énergie ?

Donner une autre unité pratique d'énergie .

Niveau intermédiaire

4-9 Quelle est la puissance électrique perdue dans un conducteur dont la résistance est 10Ω et qui est parcouru par un courant de 3 A ?

4-10 La plaque signalétique d'un fer à repasser porte l'indication suivante: puissance: 480 W; tension de service: 120 V.

a) Déterminer son courant nominal et sa résistance.

b) Calculer le courant tiré, la puissance débitée et l'énergie consommée pendant une heure si l'on branche le fer à repasser sur un réseau à 105 V.

4-11 Un fusible de 100 A possède une résistance de 0,001 ohm.

Quelle est la chaleur dissipée lorsque le fusible porte

a) le courant nominal ?

b) un courant de court-circuit de 1000 A ?

4-12 Quelle est la chute de tension dans une résistance qui dissipe une puissance de 10 W lorsqu'elle est parcourue par un courant de 2 A ?

4-13 Calculer la puissance (en kW) d'une génératrice qui débite 30 A sous une tension de 220 V.

Sachant que son rendement est de 88,5 %, calculer la puissance du moteur qui l'entraîne .

4-14 Une résistance de 100 Ω peut débiter une puissance de 200 W.

Quelle tension maximale peut-on lui appliquer ?

4-15 Pendant un court intervalle, un homme peut développer une puissance mécanique de l'ordre de 1000 W. Cependant, de façon soutenue, il ne peut débiter qu'une puissance de 15 W.

a) Exprimer ces deux puissances en horsepower.

b) Combien de kilojoules d'énergie mécanique un homme peut-il débiter pendant une journée de huit heures ?

Exprimer cette énergie en kilowattheures.

4-16 Au Québec, en 1996, la consommation annuelle moyenne par abonnement domiciliaire était de 9300 kW.h.

Quelle était la puissance moyenne utilisée, en watts?

4-17 Compte tenu de l'information donnée au problème 4-15, combien d'hommes seraient requis pour fournir, à court terme, la même puissance que la centrale de génération de Beauharnois dont la capacité installée est de 1574 MW ?

Niveau avancé

4-18 Une chaufferette de 1000W fonctionne normalement sous une tension de 120 V. Quelle puissance dégagera-t-elle si la tension baisse de 10 % ?

Quelle est, en pour cent, la diminution de puissance ?

4-19

a) Un moteur absorbe 15 A sous 120 V. Quelle est sa puissance en horsepower, si on néglige les pertes ?

b) Quelle puissance mécanique développe-t-il, si son rendement est de 90 % ?

Réponses

6) 0,5 A;

7) 7,5 A;

9) 90 W;

10a) 4 A; 30Ω; 10 b) 3,5 A; 367,5 W; 1,32 MJ;

11 a) 10 W;

11b) 1000 W;

12) 5 V;

13) 6,6 kW; 10 HP;

14) 141,4 V