Solutions des circuits à courant continu
À la section Circuits simples à courant continu, nous avons appris à résoudre les circuits série, parallèle et série-parallèle.
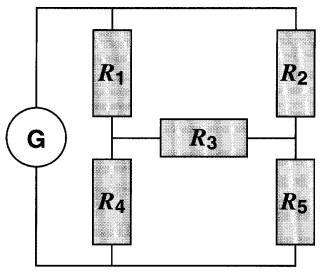
Il existe toutefois des circuits dont les composants ne sont connectés ni en série ni en parallèle, mais forment un arrangement plus complexe comme, par exemple, le circuit de la Fig. 8-1.
Figure 8-1 Circuit dans lequel aucune des résistances n'est branchée directement en série ou en parallèle avec une autre résistance.

Pour résoudre ces circuits, il faut avoir recours à la première et à la deuxième loi de Kirchhoff concernant respectivement les tensions et les courants.
Première loi de Kirchhoff
La somme algébrique des tensions dans une boucle fermée d'un circuit est égale à zéro.
Deuxième loi de Kirchhoff
La somme des courants qui arrivent à un noeud est égale à la somme des courants qui en partent.
Étudions à tour de rôle la signification de ces deux lois.
Première loi de Kirchhoff (concernant les tensions)
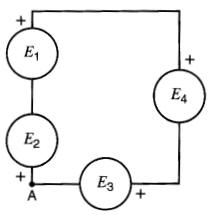
Soit une série de tensions E1, E2, E3, E4, raccordées en boucle fermée (Fig. 8-2).
Figure 8-2 Loi de Kirchhoff concernant les tensions: circuit composé d'une boucle
Elles sont désignées selon la méthode des polarités (section Conventions de signes pour tensions et courants).
Si, partant d'un point quelconque, on fait le tour de cette boucle dans le sens horaire, ou dans le sens antihoraire, on trouvera d'après cette loi que la somme des tensions est égale à zéro.
Lorsqu'on décrit la boucle, on doit affecter chaque tension d'un signe (+ ou -) correspondant à la polarité de la borne rencontrée en premier lieu.
Par exemple, sur la Fig. 8-2, en partant du point A et en décrivant la boucle dans le sens horaire, on obtient :
+ E2 - E1 + E4 + E3 = 0 (8-1)
Noter que le signe (+) précède les tensions E2, E4 et E3 parce que dans chaque cas on rencontre d'abord la borne positive.
Par contre, si l'on choisit le sens antihoraire et toujours en partant du point A, on obtient :
- E3 - E4 + E1 - E2 = 0 (8-2)
Pour un circuit plus complexe (Fig. 8-3), on applique la même règle: il suffit de suivre une boucle quelconque et, pourvu que l'on revienne au point de départ, la somme des tensions est toujours nulle.
Figure 8-3 Circuit composé de plusieurs boucles
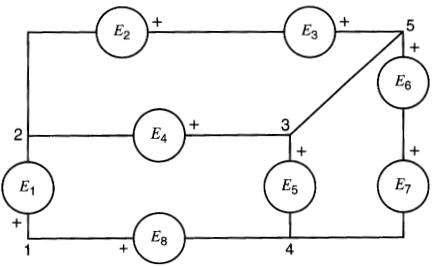
Pour le circuit de la Fig. 8-3, on vérifiera les équations suivantes:
en suivant la
boucle 1 -> 2 -> 3 -> 4 -> 1 (8-3)
on obtient
+ E1 - E4 + E5 - E8
= 0
en suivant la boucle 1 -> 4 -> 5 -> 3 -> 2 -> 1
on obtient
+ E8 - E7 - E6 + E4 - E1 = 0 (8-4)
en suivant la boucle 3 -> 2 -> 5 -> 3
on obtient
+ E4 - E2 - E3 = 0 (8-5)
Les tensions dont on parle dans la première loi de Kirchhoff ne sont pas forcément des sources de tension mais elles peuvent être produites par le passage d'un courant dans une résistance.
Quel signe faut-il donner à ces tensions?
Considérons, par exemple, le circuit simple de la Fig. 8-4.
Figure 8-4 Circuit contenant une résistance
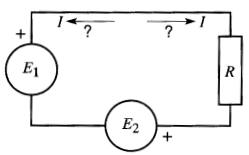
À cause de leur polarité les sources E1 et E2 ont tendance à produire les courants qui circulent respectivement dans les sens horaire et antihoraire.
Si l'on ne connaît pas la valeur de E1 ni celle de E2, on ne peut pas en déduire le sens que prendra le courant I résultant.
On choisit alors un sens arbitraire.
Prenons, par exemple, le sens horaire comme sur la Fig. 8-5.
Figure 8-5 Choix d'un sens arbitraire du courant
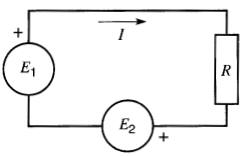
Le courant I produira une tension RI à travers la résistance. Le signe de cette tension dépend de la direction du courant et du sens dans lequel on parcourt la boucle.
Lorsque l'on décrit la boucle, la tension RI sera précédée d'un signe (+) si on traverse la résistance dans le sens du courant et d'un signe (-), si on la traverse dans le sens contraire.
Par exemple, en parcourant le circuit de la Fig. 8-5 dans le sens horaire, on obtient:
- E1 + RI + E2 = 0 (8-6)
La tension RI est précédée du signe (+) parce que l'on traverse la résistance dans le sens du courant.
Si, par contre, on décrit la boucle dans le sens antihoraire, on obtient:
- E2 - RI + E1 = 0 (8-7)
La tension RI est précédée du signe (-) parce que l'on traverse la résistance dans le sens contraire du courant.
N'étant pas sûr du sens réel du courant, on aurait pu choisir un courant de sens opposé à celui de la Fig. 8-5.
Dans ce cas, si l'on décrit la boucle dans le sens horaire (Fig. 8-6), on obtient l'équation:
- E1 - RI + E2 = 0
Figure 8-6 Choix d'un sens arbitraire du courant qui est l'opposé de celui de la figure 8-5
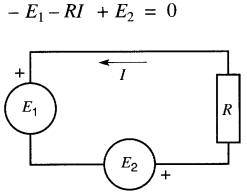
Bien que certains termes changent de signe suivant le sens choisi pour le courant, la résolution des équations fournit toujours la bonne valeur et le bon sens du courant.
Exemple 8-1
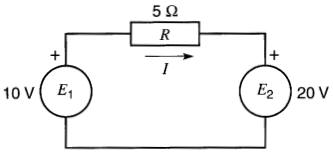
Trouver la valeur et le sens du courant 1 dans le montage de la Fig. 8-7.
Figure 8-7 Voir exemple 8-1
Solution
Supposons que le courant circule de gauche à droite dans la résistance, et suivons le circuit dans le sens horaire; on obtient:
- E1 + RI + E2 =0
Soit, en passant aux valeurs numériques :
- 10 + 5I + 20=0
5I = - 10
I = -2A
La valeur du courant est de 2 ampères; le signe (-) indique que son sens réel est l'inverse de celui que nous avions supposé. Un courant de 2 ampères circule donc dans le sens antihoraire, soit de droite à gauche dans la résistance.
Exemple 8-2
Soit quatre sources ayant les tensions et polarités indiquées a la Fig. 8-8a.
Figure 8-8a Quatre sources indépendantes. Voir exemple 8-2.
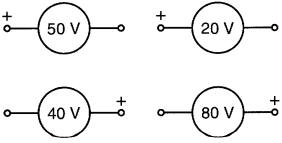
Les sources sont alors raccordées en série suivant le schéma de la Fig. 8-8b.
Figure 8-8b Les sources sont raccordées en série, créant ainsi deux bornes A, B.
La tension E entre ces bornes est supposée (+) du côté A
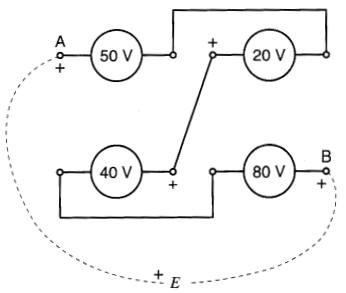
Trouver la valeur et la polarité de la tension entre les bornes «ouvertes» A et B.
Solution
On peut choisir une polarité arbitraire pour une tension tout comme on peut choisir un sens quelconque pour un courant.
Disons que la tension E entre les bornes A et B est positive (+) du côté de la borne A (Fig. 8-8b).
Suivons maintenant la boucle formée par les quatre sources en série et le chemin en pointillé (dans l'air) reliant les bornes ouvertes.
En adoptant le sens antihoraire, on obtient:
+ E + 80 - 40 + 20 - 50 = 0
E = -10V
La tension entre A et B est donc de 10 V, et la polarité est l'inverse de celle qu'on avait choisie:
la borne A est donc négative par rapport à la borne B.
Deuxième loi de Kirchhoff (concernant les courants)
La deuxième loi de Kirchhoff exprime l'impossibilité d'accumuler des électrons en un point.
Dans un circuit électrique, on appelle nœud un point commun où aboutissent deux ou plusieurs conducteurs.
Considérons les courants I1 , I2,I3 et I4 circulant dans les sens indiqués sur la Fig. 8-9.
Figure 8-9 Loi de Kirchhoff concernant les courants
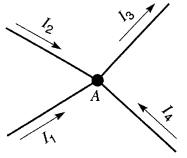
D'après cette loi, la somme des courants qui arrivent au noeud A est égale à la somme des courants qui en repartent.
On obtient donc:
I1 + I2 + I4 = I3 (8-9)
Dans le cas de la Fig. 8-10, on aurait au nœud B :
Figure 8-10 Le point B est un noeud
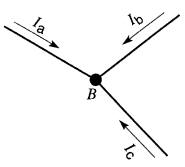
Ia +Ib +Ic =0 (8-10)
car, d'après le sens des flèches, aucun courant ne part du nœud B.
La deuxième loi de Kirchhoff permet de calculer la valeur et le sens du courant circulant dans un conducteur quelconque lorsque les courants dans les autres conducteurs arrivant au même noeud sont connus.
Exemple 8-3
Trouver la valeur du courant dans le fil X (Fig. 8-11), connaissant la valeur et le sens des courants dans les quatre autres fils.
Figure 8-11 On cherche la valeur et le sens du courant dans le fil X Voir exemple 8-3
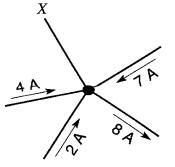
Solution
Supposons que le fil X porte un courant I qui se dirige vers le nœud (Fig. 8-12).
Figure 8-12 Voir exemple 8-3
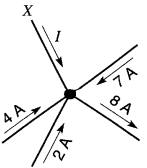
D'après la deuxième loi de Kirchhoff, on obtient:
1+ 4+ 7+ 2= 8
I = -5A
Le courant dans le fil est de 5 A et le signe (-) nous indique qu'il circule dans le sens opposé à celui de la flèche.
Application pratique aux circuits
Connaissant la façon d'appliquer les deux lois de Kirchhoff, nous sommes en mesure de résoudre les circuits les plus complexes.
Exemple 8-4
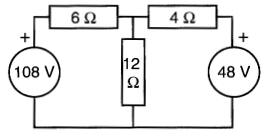
Calculer les courants et les tensions pour chacune des résistances de la Fig. 8-13.
Figure 8-13 Voir exemple 8-4
Solution
On se donne des sens de courant arbitraires pour I1 et I2 (Fig. 8-14) et, afin d'éviter l'emploi d'un troisième courant inconnu, on indique un courant (I1 + I2) dans la résistance de 12Ω.
Figure 8-14 On choisit des sens arbitraires pour les courants II et I2. Voir exemple 8-4
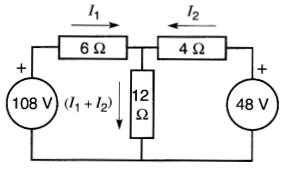
La direction de (I1 + 12) n'est pas arbitraire; elle doit être choisie de façon à respecter la deuxième loi de Kirchhoff.
On constate, Fig. 8-14, que la somme des courants I1 et 12 arrivant au noeud A est égale au courant (I1 + I2) qui en sort.
En décrivant la boucle formée par les deux sources et les résistances de 6Ω et 4 Ω, on obtient d'après la première loi de Kirchhoff:
-108 + 6I1 - 4I2 + 48 = 0 (1)
Ensuite, on peut choisir la boucle formée par la source de 108 V et les résistances de 6Ω et 12Ω.
-108 + 6I1 + 12(I1 + I2 ) = 0 (2)
On obtient ainsi un système de deux équations à deux inconnues I1 et I2. On peut donc trouver la valeur des courants I1 et I2.
I1 = 8A, I2 =-3A et par suite (I1 + 12 ) = 8A - 3A = 5A
Les courants réels circulent dans le sens indiqué sur la Fig. 8-15.
Figure 8-15 Valeurs et sens réels des courants. Voir exemple 8-4
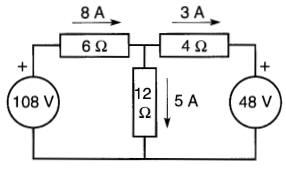
La «source» de 48 V est en réalité une charge puisque le courant de 3 A entre par la borne (+).
Exemple 8-5
Trouver les tensions et les courants dans chacune des branches du circuit de la Fig. 8-16.
Figure 8-16 Voir exemple 8-5. On cherche la valeur de la tension et du courant dans chaque résistance
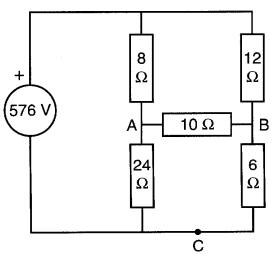
Solution
On donne aux courants I1, I2 et I3 des sens arbitraires (Fig. 8-17).
Figure 8-17 On choisit des sens arbitraires pour les courants I1, I2 et I3. Voir exemple 8-5
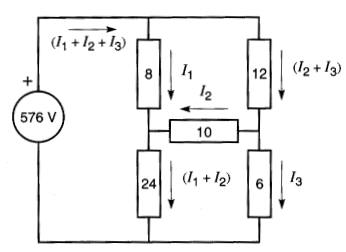
En utilisant le minimum de courants inconnus on réduit le nombre d'équations à résoudre.
Cependant, une fois les sens de I1, I2 et I3 choisis, les sens des courants (I1 + I2), (I2 + I3) et (I1 + I2 + I3) sont imposés par la deuxième loi de Kirchhoff.
On obtient le système d'équations suivant:
8I1 -10I2 - 12(I2 +I3 ) = 0 (1)
10I2 + 24 ( I1 + I2 ) - 6I3 = 0 (2)
- 576 + 8I1 - 10I2 + 6I3 = 0 (3)
après résolution, on trouve :
I1 = + 27A (I1 +I2 ) = +15A
I2 = - 12A (I2 +I3 ) = +28A
I3 = + 40A (I1 + I2 + I3 ) = +55A
On aurait pu résoudre ce problème en se donnant plusieurs courants arbitraires, comme sur la Fig. 8-18.
Figure 8-18 On peut résoudre le circuit en choisissant six courants de sens arbitraires au lieu de trois. Toutefois, cela augmente le nombre d'équations à résoudre
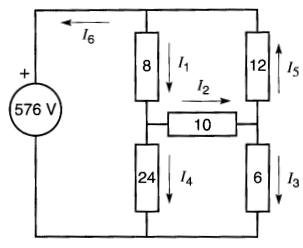
Dans ce cas, en parcourant les boucles, on obtient :
8I1 + 10I2 + 12I5 = 0 (4)
-24I4 + 10I2 +6I3 =0 (5)
- 576 + 8I1 + 24I4 = 0 (6)
La deuxième loi de Kirchhoff nous fournit les équations pour les courants:
I1 =I2 +I4 (7)
I5 = I1 + I6 (8)
I2 = I5 + I3 (9)
On obtient donc un système de 6 équations (équations (4) à (9)) à 6 inconnues, ce qui permet de trouver les 6 courants.
On voit, cependant, l'avantage de réduire au départ le nombre de courants inconnus comme on l'a fait sur la Fig. 8-17.
Théorème de Thévenin
Bien que les lois de Kirchhoff permettent de résoudre n'importe quel circuit, si compliqué soit-il, on peut souvent en simplifier la solution en utilisant l'artifice du théorème de Thévenin, qui est d'ailleurs basé sur les lois de Kirchhoff.
Énoncé du théorème de Thévenin
Tout circuit à deux bornes ouvertes A et B composé de plusieurs sources et de plusieurs résistances peut être remplacé par une source unique E en série avec une résistance unique R.
Soit un circuit composé de plusieurs sources et de plusieurs résistances, représentées respectivement par des cercles et des petits rectangles (Fig. 8-19).
Figure 8-19 Montage très complexe où l'on cherche la tension et le courant dans la résistance Z
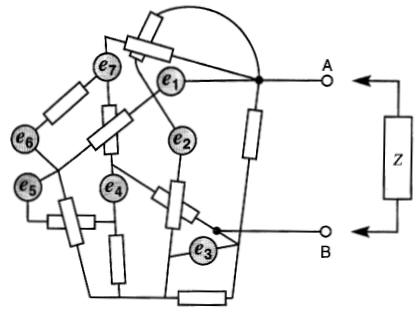
Le montage possède deux bornes A et B lesquelles peuvent être raccordées à une résistance Z.
D'après le théorème de Thévenin, ce circuit complexe peut être remplacé par le circuit simple de la Fig. 8-20.
Figure 8-20 Circuit équivalent du montage de la figure 8-19, selon le théorème de Thévenin
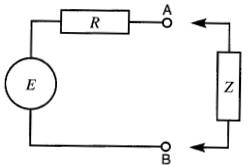
Dans ce circuit simple:
a) La tension de Thévenin E est celle qui apparaît entre les bornes A et B du circuit de la Fig. 8-19 (circuit ouvert).
b) La résistance R de Thévenin est celle que l'on mesurerait entre les bornes A et B si toutes les sources du circuit de la Fig. 8-19 étaient court-circuitées.
En comparant le circuit de la Fig. 8-20 avec celui de la Fig. 8-19, on comprend pourquoi le théorème de Thévenin est un outil puissant : il permet de trouver le courant dans une résistance Z quelconque sans qu'on ait à résoudre le circuit au complet.
Appliquons-le à l'exemple 8-4 étudié précédemment.
Exemple 8-6
Trouver la valeur et le sens du courant circulant dans la résistance de 6Ω (Fig. 8-21).
Figure 8-21 On cherche la valeur du courant circulant dans la résistance de 6Ω. Voir exemple 8-6
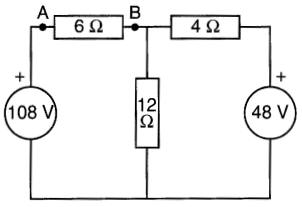
Solution
Le théorème de Thévenin permet de trouver la tension et le courant dans une résistance à la fois. Puisqu'il s'agit de la résistance de 6Ω, on doit déterminer le circuit équivalent de Thévenin entre les bornes A et B (Fig. 8-21).
Ainsi, trouvons d'abord la tension de Thévenin E apparaissant entre ces bornes à circuit ouvert, c'est-à-dire en enlevant la résistance de 6Ω (Fig. 8-22).
Figure 8-22 On trouve EAB lorsque la résistance de 6Ω est enlevée du circuit. Voir exemple 8-6
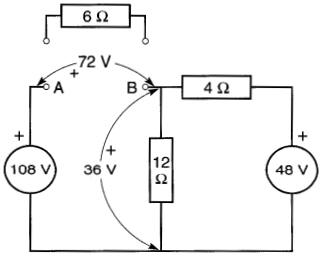
La tension aux bornes de la résistance de 12Ω est alors:
48V x (12Ω / (4Ω+12Ω)) = 36V
Il s'ensuit que la tension entre A et B vaut (108 - 36) = 72 V.
La tension de Thévenin E (Fig. 8-20) vaut donc 72 V.
Ensuite, en supposant que les sources de 108 V et de 48 V soient mises en court-circuit, on calcule la résistance vue entre les bornes A et B (Fig. 8-23).
Figure 8-23 On calcule la résistance entre les bornes A,B lorsque les sources de tension sont en court-circuit. Voir exemple 8-6
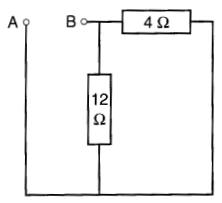
Elle est composée d'une résistance de 12Ω en parallèle avec une résistance de 4Ω, soit une résistance de 3Ω.
Celle- ci est la résistance R de Thévenin. Le circuit équivalent de Thévenin est donc composé d'une résistance de 3Ω en série avec une tension de 72 V (Fig. 8-24).
Figure 8-24 Circuit équivalent de Thévenin où E (Thévenin) = 72 V et R (Thévenin) = 3Ω. Voir exemple 8-6
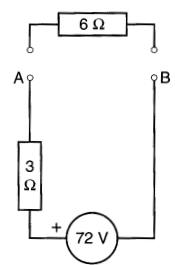
Figure 8-25 Calcul du courant dans la résistance de 6Ω
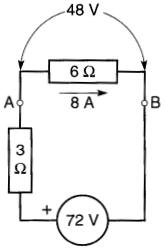
Lorsque la résistance de 6Ω est branchée entre les bornes A et B (Fig. 8-25), on trouve qu'elle porte un courant de
72 V /( 3Ω + 6Ω) = 8A, et que ce courant circule de gauche à droite dans la résistance.
On pourrait trouver les courants circulant dans les deux autres résistances par la même méthode de Thévenin.
Cependant, on peut les calculer encore plus simplement en suivant le raisonnement suivant:
La chute de tension dans la résistance de 6Ω étant de 8 A x 6Ω = 48 V, la tension aux bornes de la résistance de 12Ω est (108 - 48) = 60 V.
Par conséquent, le courant dans celle-ci est de 5A. Il s'ensuit que la résistance de 4Ω porte un courant de (8 - 5) = 3A circulant dans le sens indiqué sur la Fig. 8-26.
Figure 8-26 Calcul des courants et des tensions dans tous les éléments du circuit. Voir exemple 8-6.
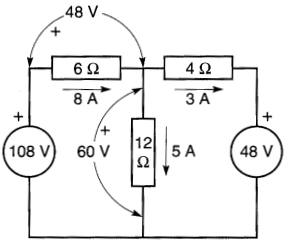
Les courants respectifs sont bien identiques à ceux calculés précédemment, et affichés sur la Fig. 8-15.
Courants de maille
Pour la résolution des circuits complexes, on emploie souvent la méthode des courants de maille.
Par exemple, dans le cas du circuit de la Fig. 8-27, on utilisera les courants I1 , I2 et 13 circulant respectivement dans les mailles (ou boucles) X, Y, Z du circuit.
Figure 8-27 Résolution d'un circuit par la méthode des courants de maille
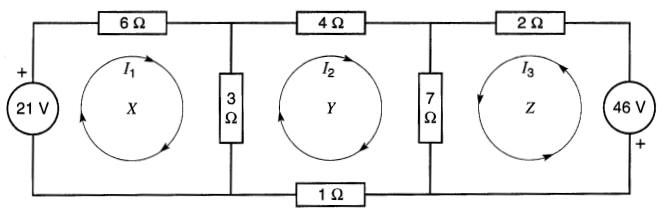
Ainsi, II circule dans la boucle X, composée des résistances de 6Ω et 3Ω et de la source de 21V.
De la même façon, le courant 12 circule dans la boucle Y, composée des résistances de 3Ω, 4Ω, 7Ω et 1Ω.
Les polarités des sources de 21V et de 46V sont imposées par le problème, mais le sens choisi pour les courants de maille est arbitraire.
Pour écrire les équations du circuit, on suit la méthode habituelle en parcourant chacune des mailles à tour de rôle. Il est utile de grouper ensemble toutes les résistances associées à chacun des courants de maille.
Par exemple, en décrivant la maille X dans le sens horaire, on écrira:
-21 + (6 + 3)I1 -3I2 = 0 (8-11)
Les résistances de 6Ω et 3Ω sont groupées ensemble, et le signe (-) figurant devant le terme 3I2 signifie simplement que l'on se déplace en sens inverse de I2 en décrivant la maille X dans le sens horaire. De la même façon, pour la deuxième maille Y, on écrira :
(3 + 4 + 7 + 1)I2 -3I1 +7I3 =0 (8-12)
Enfin, en décrivant la troisième maille Z, dans le sens antihoraire, on aura:
+46 + (2 + 7)I3 + 7I2 = 0 (8-13)
On obtient donc un système de 3 équations:
9I1 - 3I2 = 21
-3I1 +15I2 +7I3 = 0
7I2 +9I3 =-46
De ces équations, on peut déduire les trois courants de maille:
I1 =+4A, I2 =+5A, I3 =-9A
Maintenant, il est facile de trouver la valeur et le sens réel de tous les courants (Fig. 8-28).
Figure 8-28 Calcul des courants dans le circuit de la figure 8-27
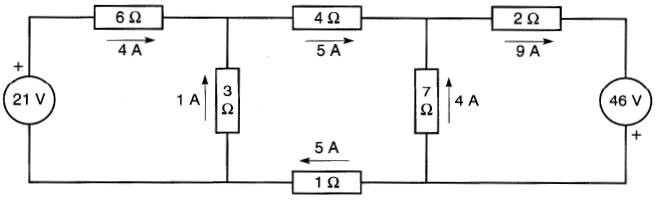
Le grand avantage de cette méthode des courants de maille réside dans le fait qu'on utilise un nombre réduit d'équations.
Il suffit d'employer autant de courants inconnus que le réseau possède de mailles.
Théorème de superposition
Enfin, mentionnons une dernière méthode permettant de résoudre les circuits, basée également sur les lois de Kirchhoff.
Elle utilise le théorème de superposition.
D'après ce théorème, le courant circulant dans un élément de circuit est égal à la somme algébrique des courants qui seraient produits dans cet élément par chacune des sources agissant seule, les autres sources étant remplacées par des court-circuits.
Exemple 8-7
Trouver les courants circulant dans chacune des résistances de la Fig. 8-29 en utilisant le théorème de superposition.
Figure 8-29 Résolution d'un circuit utilisant le théorème de superposition
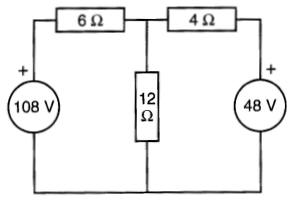
Solution Considérons d'abord le circuit comme si la source de 108 V agissait seule, la source de 48 V étant remplacée par un court-circuit, (Fig. 8-30).
Figure 8-30 Courants produits lorsque la source de 108 V agit seule. Voir exemple 8-7
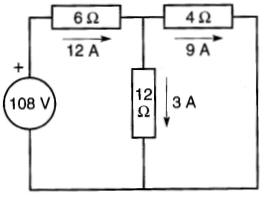
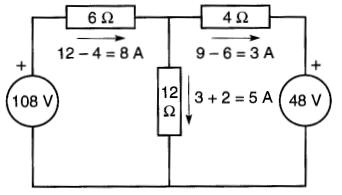
On trouve facilement les courants de 3 A, 9 A et 12 A circulant dans les résistances de la Fig. 8-30.
Considérons maintenant le circuit comme si la source de 48 V agissait seule, celle de 108 V étant, à son tour, remplacée par un court-circuit. Les courants résultants sont donnés à la Fig. 8-31.
Figure 8-31 Courants produits lorsque la source de 48 V agit seule. Voir exemple 8-7
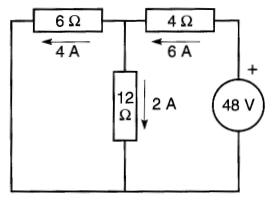
D'après le théorème de superposition, lorsque les deux sources fonctionnent, les courants circulant dans chaque résistance sont égaux à la somme algébrique des courants individuels, obtenus respectivement dans les circuits des Fig. 8-30 et 8-31.
Le résultat est donné à la Fig. 8-32. On vérifie que les courants sont identiques à ceux trouvés dans l'exemple 8-4.
Figure 8-32 Superposition des courants créés par les deux sources. Voir exemple 8-7
Utilisation de la méthode des deux indices
Dans les sections ci-dessous nous avons employé la méthode des polarités (section Conventions de signes pour tensions et courants) pour décrire les tensions. Nous pouvons aussi utiliser la méthode des deux indices.
L'exemple suivant montre la façon d'appliquer cette méthode pour formuler les équations selon les lois de Kirchhoff. La Fig. 8-33 montre un circuit composé de trois sources et de quelques résistances. Les noeuds sont identifiés par des chiffres 1 à 6.
Figure 8-33
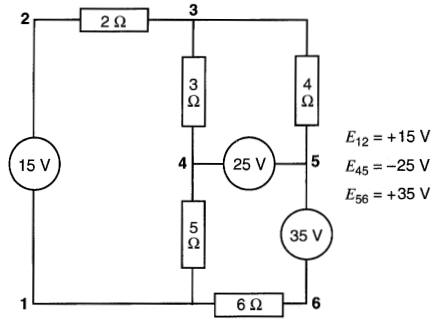
La valeur et la polarité des sources E12, E45, E56 sont indiquées dans un tableau séparé, faisant partie de la figure. Ces données représentent des valeurs imposées.
Nous désirons trouver les courants qui circulent dans tous les éléments du circuit. Pour ce faire, nous répétons la figure en y inscrivant, dans trois des branches, les courants I1 , I2, I3. Le sens de ces courants sont arbitraires (Fig. 8-34).
Figure 8-34
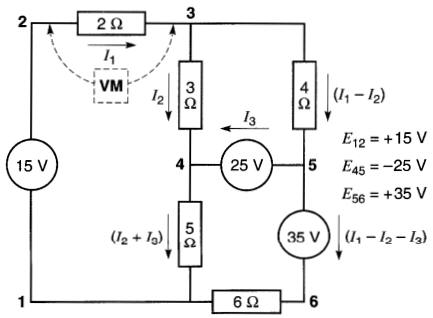
Cependant, la valeur et le sens des courants dans les autres éléments du circuit doivent respecter la deuxième loi de Kirchhoff.
Par exemple, une fois choisis les sens des courants I2 et I3 dans les éléments de 3Ω et de 25V, le courant circulant dans la résistance de 5Ω est nécessairement (I2 +I3), et il doit nécessairement sortir du nceud 4.
Ensuite, on écrit les équations de tension selon la première loi de Kirchhoff. En parcourant les boucles, nous
choisirons de façon arbitraire le sens horaire ou antihoraire. Les tensions portent alors les indices correspondant à la séquence des nceuds rencontrés.
Parcourons, par exemple, la boucle 1-2-3-4-1 dans le sens horaire. En partant du point 1, on peut écrire :
E12 + 2I1 + 3I2 + 5(I2 +I3) = 0 (8-14)
Ensuite, parcourons la boucle 3-5-4-3 dans le sens horaire, en partant du point 4.
On écrit: -3I2 + 4(I1 - I2) + E54 = 0 (8-15)
Décrivons maintenant la boucle 4-1-6-5-4 dans le sens antihoraire en partant, disons, du nceud 5.
On obtient: E54 + 5(I2 + I3) - 6(I1 - I2 - I3) + E65 = 0 (8-16)
Sachant que E12 = +15 V, E45 = -25 V, et E56 = +35 V,
on substitue ces valeurs dans les expressions précédentes, ce qui donne les trois équations suivantes :
+15 + 2I1 + 3I2 + 5(I2+I3) = 0 (8-17)
-3I2 + 4(I1 -I2) + 25 = 0 (8-18)
25+5(12 + 13)-6(I,-12 -13)-35=0 (8-19)
La résolution de ces équations donne les résultats suivants.
Le lecteur aura avantage à les vérifier.
I1 = -4,70A, I2 = 0,89A, I3 = -2,54 A
Les autres courants sont faciles à calculer. Leur valeur et leur sens réél, de même que la polarité réelle des tensions, sont montrés à la Fig. 8-35.
Figure 8-35
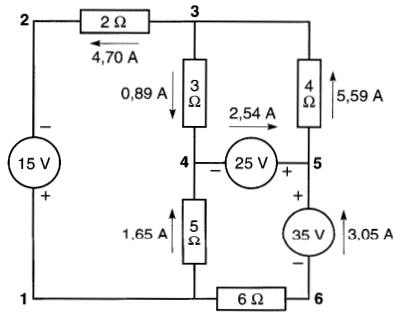
Tension entre deux points d'un circuit
Il arrive souvent que l'on cherche la valeur d'une tension entre deux points quelconques d'un circuit. Dans ce cas, il suffit d'imaginer qu'un voltmètre soit branché entre ces deux points.
En parcourant la boucle créée par le «voltmètre» et les éléments du circuit entre ces deux points, on écrit l'expression habituelle de la première loi de Kirchhoff.
Par exemple, si on cherche la tension E23 aux bornes de la résistance de 2Ω (Fig. 8-34), il suffit de parcourir la «boucle» formée par le voltmètre imaginaire VM et cet élément.
Ainsi, on écrit E23 - 2It = 0, ce qui donne
E23 = 2I1, = 2Ω X (- 4,7 A) = - 9,4 V.
Donc, la tension est de 9,4 V et la borne 2 est négative par rapport à la borne 3.
De même, on peut trouver la tension E31 entre les bornes 3 et 1, en décrivant la boucle
E31 + EI2 + 2I1 = 0
ce qui donne
E31 =-E12 - 2I1 = -15V - (2Ω(-4,70 A))= -5,6V
Utilisation de la notation hybride Nous avons vu comment on peut résoudre les circuits en utilisant pour les tensions, soit la méthode des deux indices, soit la méthode des polarités. Il est parfois commode d'utiliser les deux notations dans un même circuit. Nous l'appelons alors la notation hybride.
Considérons une source de tension Es dont une des bornes porte le signe (+), selon la méthode des polarités (Fig. 8-36a).
Figure 8-36 Circuit hybride
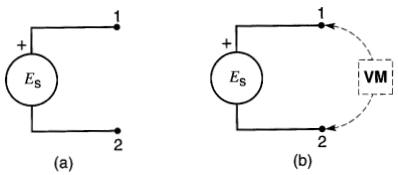
L'autre borne est évidemment négative (-). La borne (+) porte aussi le chiffre 1, et la borne (-) porte le chiffre 2, selon la méthode des deux indices.
Supposons qu'un voltmètre fictif VM soit branché aux bornes de la source (Fig. 8-36b). En parcourant la boucle ainsi formée dans le sens horaire, on peut écrire l'équation
E12 - Es = 0
Par conséquent, on obtient E12 = Es
On conclut que, dans un circuit, on peut simultanément exprimer les tensions selon la méthode des deux indices et selon la méthode des polarités.
La résolution d'un tel circuit se fait par les méthodes que nous venons de décrire.
Exemple 8-8
La Fig. 8-37 montre un circuit où E 8 V (notation selon la méthode des polarités ) et EA = + 28 V (notation selon la méthode des deux indices).
Figure 8-37 Circuit hybride. Voir exemple 8-8
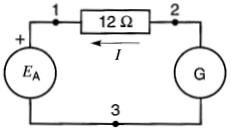
On désire connaître a) la valeur et le sens du courant circulant dans le circuit et b) la nature de G (source ou charge L.
Solution
a) On choisit d'abord un sens arbitraire pour le courant I, ce qui nous permet d'écrire l'équation suivante, en parcourant la boucle dans le sens horaire :
-12I + E23 - EA = 0
En substituant les valeurs données à E23 et à EA on obtient
-12I+ (+28) - (-8) = 0
donc ,
-12I + 36 = 0, soit I=+3A
Le signe (+) indique que le courant circule réellement dans le sens de la flèche.
b) Puisque E23 = +28 V, la borne 2 est (+) par rapport à la borne 3.
Comme le courant sort de la borne (+), G est une source.
Résumé
Dans cette section nous avons appris à utiliser deux lois fondamentales pour la résolution des circuits à courant continu.
Selon la première loi de Kirchhoff, la somme des tensions autour d'une boucle est nulle.
Selon la deuxième loi de Kirchhoff, la somme des courants arrivant à un noeud est nulle.
Alliées à la loi d'Ohm, ces deux lois permettent de trouver les courants et les tensions dans les branches des circuits même les plus complexes.
Pour l'écriture des équations de tension, nous avons vu que l'on peut utiliser indifféremment la méthode des deux indices, la méthode des polarités ou une combinaison de ces deux méthodes.
En appliquant la première loi de Kirchhoff, on a vu qu'on peut parcourir une boucle dans le sens horaire ou antihoraire, sans que cela change le résultat final.
Cependant, en pratique, on choisit habituellement le sens horaire. Il est parfois plus rapide d'utiliser d'autres méthodes dérivées des lois de Kirchhoff.
Le théorème de Thévenin permet de trouver la tension et le courant dans une branche particulière d'un circuit. Cette méthode consiste à remplacer la portion du circuit alimentant la branche d'intérêt par une source de tension branchée en série avec une résistance. Le théorème de superposition est utile lorsque l'on doit résoudre un circuit alimenté par plusieurs sources.
On constate que les outils permettant de résoudre les circuits ne manquent pas ; mais tout comme on n'emploie pas une masse pour enfoncer un clou, on n'utilisera pas le théorème de Thévenin pour résoudre un simple circuit série. Seule l'expérience peut nous apprendre quelle méthode est la plus rapide.
PROBLÈMES
8-1 Écrire les équations des circuits (a), (b), (c), (d), de la Fig. 8-38.
Figure 8-38 Voir problèmes 8-1, 8-2
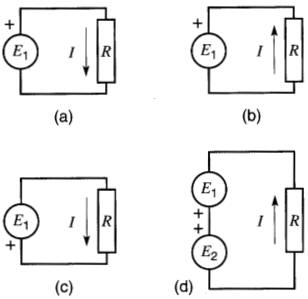
8-2 Dans la Fig. 8-38d, E1 = + 10V, E2 = -30 V et R = 5Ω. Trouver la valeur et le sens réel du courant I.
8-3 Énoncer la première et la deuxième loi de Kirchhoff.
8-4 Énoncer le théorème de Thévenin.
8-5 Trouver la valeur et le sens réel du courant I pour les nceuds (a), (b), (c) de la Fig. 8-39.
Figure 8-39 Voir problème 8-5
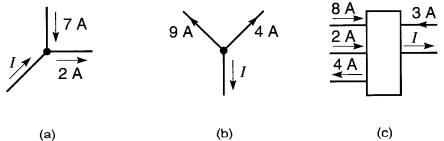
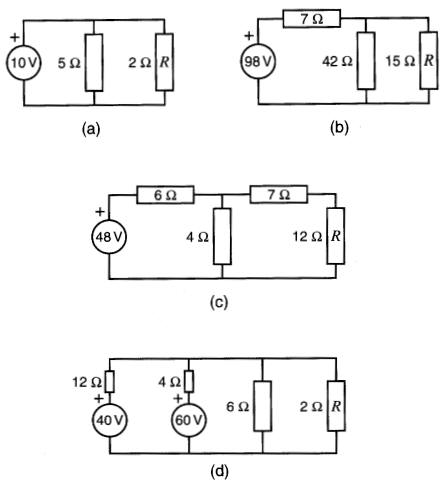
8-6 En utilisant le théorème de Thévenin, déterminer pour les circuits (a), (b), (c), (d) de la Fig. 8-40, la valeur et le sens du courant dans chacune des résistances R.
Figure 8-40 Voir problème 8-6
Niveau avancé
8-7 En utilisant le principe de superposition, déterminer les tensions et les courants dans les circuits (a) et (b) de la Fig. 8-41.
Figure 8-41 Voir problèmes 8-7, 8-8
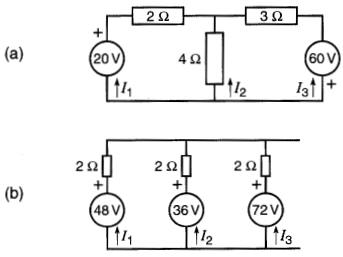
8-8 En utilisant la méthode des courants de maille, déterminer les valeurs de I1 et de I3 dans la Fig. 8-41, circuits (a), (b).
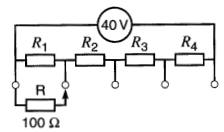
8-9 Le circuit de la Fig. 8-42 représente un diviseur de potentiel résistif permettant d'alimenter une résistance R à une tension de 10 V, 20 V, 30 V ou 40 V.
Déterminer les valeurs de R1, R2, R3 et R4, sachant que R1 + R2 + R3 + R4 = 200Ω et que R = 100Ω.
Figure 8-42 Voir problème 8-9
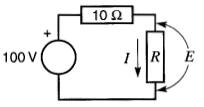
8-10 Une source de 100 V possède une résistance interne de 10Ω (Fig. 8-43).
Déterminer la valeur du courant I et de la tension E aux bornes de la résistance R, à mesure que cette dernière varie de zéro à l'infini.
Pour quelle valeur de R la dissipation de puissance est-elle maximale ?
Figure 8-43 Voir problème 8-10
8-11 Dans la Fig. 8-1 on donne les valeurs suivantes:
R1 = 10Ω, R2= 20Ω, R3 = 30Ω, R4 = 40 Ω, R5 = 50Ω et la tension de la source G est de 350V.
En utilisant le théorème de Thévenin, calculer la valeur du courant dans la résistance R3.
8-12 Une source d'alimentation donne une tension de 25V à circuit ouvert. Lorsqu'on lui applique une charge de 10A, la tension à ses bornes baisse à 24,9V.
Calculer:
a) la résistance interne de la source
b) la puissance maximale qu'elle peut débiter dans une charge dont la résistance est variable 8-13
En utilisant le théorème de Thévenin seulement, calculer le courant dans la résistance de 3Ω de la Fig. 8-27.
Ensuite, déterminer par des méthodes très élémentaires, le courant dans l'élément de 6Ω et la tension aux bornes de l'élément de 7Ω.
8-14 Dans le circuit de la Fig. 8-2, EI = +10V, E2 = -2V, E3 = -13V, E4 = +6V. Calculer la valeur et le sens réel du courant dans le circuit, sachant que chaque source possède une résistance interne de 2Ω.
8-15 Dans la Fig. 8-21, quelle résistance doit-on placer en parallèle avec l'élément de 12Ω si l'on désire que le courant dans l'élément de 4Ω soit nul ?
8-16 Dans la Fig. 8-21, si l'on place une résistance de 10Ω entre les bornes positives des deux sources, quel sera le courant dans cette résistance? Quelles seront les nouvelles valeurs du courant dans les autres éléments résistifs ?
8-17 Dans la Fig. 8-21, si l'on intervertit la polarité de la source de 48V, quel sera la valeur du courant dans la résistance de 12Ω ?
8-18 Dans la Fig. 8-26, si l'on branche une résistance de 14Ω en parallèle avec la résistance de 6Ω, quelle sera la tension à ses bornes ? (Utiliser de préférence le théorème de Thévenin.)
8-19 Dans la Fig. 8-1, si le courant dans R3 est nul, prouver que R1R5 = R2R4 quelle que soit la tension de la source.
8-20 Dans la Fig. 8-44 la résistance de 100Ω dissipe 4 fois plus de chaleur que la résistance R2.
Calculer la puissance de la génératrice et la valeur de R, sachant que la source débite un courant de 6A.
8-21 Dans la Fig. 8-2, E1 = +10V, E2 = +17V et E3 = -23V. Calculer la valeur de E4.
8-22 Dans la Fig. 8-5, E1 = +25V, E2 = -11V et R = 3Ω.
Déterminer la valeur et le sens de I.
8-23 Dans la Fig. 8-16 on veut remplacer la résistance de 12Ω par une autre afin que le courant soit nul dans la résistance de 10Ω.
Quelle résistance doit-on utiliser?
8-24 Dans la Fig. 8-16, si l'on enlève la résistance de 10Ω, calculer la nouvelle valeur de la tension entre les bornes A et B.
8-25 Dans la Fig. 8-45, on désire remplacer le circuit entre les bornes A et B par un autre composé d'une seule source de tension E en série avec une résistance R.
En utilisant le théorème de Thévenin, déterminer la valeur de E et de R.
Figure 8-45 voir problème 8-25
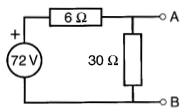
8-26 Dans la Fig. 8-46, on désire remplacer le circuit entre les bornes A et B par un autre composé d'une seule source de tension E en série avec une résistance R.
En utilisant le théorème de Thévenin, déterminer la valeur de E et de R.
Figure 8-46 Voir problème 8-26
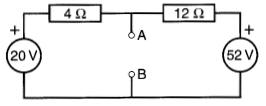
8-27 Dans la Fig. 8-47, on désire remplacer le circuit entre les bornes A et B par un autre composé d'une source de tension E en série avec une résistance R.
En utilisant le théorème de Thévenin, déterminer la valeur de E et de R.
Figure 8-47 Voir problème 8-27
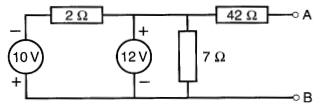
Réponses
1a) -E1+RI=0; 1b) E1 +RI=0; 1e) EI + RI=0; 1d)- E1+E2+RI=0;
2)+8A;
5a)-5A; 5b)-13A; 5c)+9A;
6a) +5A; 6b) +4A; 6c) +0,897A; 6d) +9,17A;
7a) I1=+14,6A;I2=+2,3A; I3=-16,9A; 7b) I1= -2A; I2=-8A; I3=+10A;
8a) I1=+14,6A; I3=-16,9A; 8b) I1=-2A; I3=+10A;
9) R1 = 73,2Ω; R2 = 68,2Ω; R3 = 37,2Ω; R4 = 21,4Ω;
10) 10Ω;
11) 0,574A;
12a) 10 mΩ; 12b) 15 625 W;
13) 1A; 4A, 28V;
14) 2,375A;
15) 8Ω;
16) 6A; mêmes valeurs;
17) 1A; 18) 42V;
20) 2880W; 400Ω
